数学:1.2.2《空间中的平行关系》课件(1)(新人教b版必修2)
文档属性
| 名称 | 数学:1.2.2《空间中的平行关系》课件(1)(新人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 146.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-28 12:18:00 | ||
图片预览





文档简介
课件23张PPT。1.2.2空间中的平行关系(1)一. 平行直线 1. 平行直线的定义:同一平面内不相交的两条直线叫做平行线. 2. 平行公理:过直线外一点有且只有一条直线和这条直线平行.3. 公理4:平行于同一直线的两条直线互相平行,此性质又叫做空间平行线的传递性.公理4的符号表述为:a//c,b//c a//b.公理4反映了两条直线的位置关系.
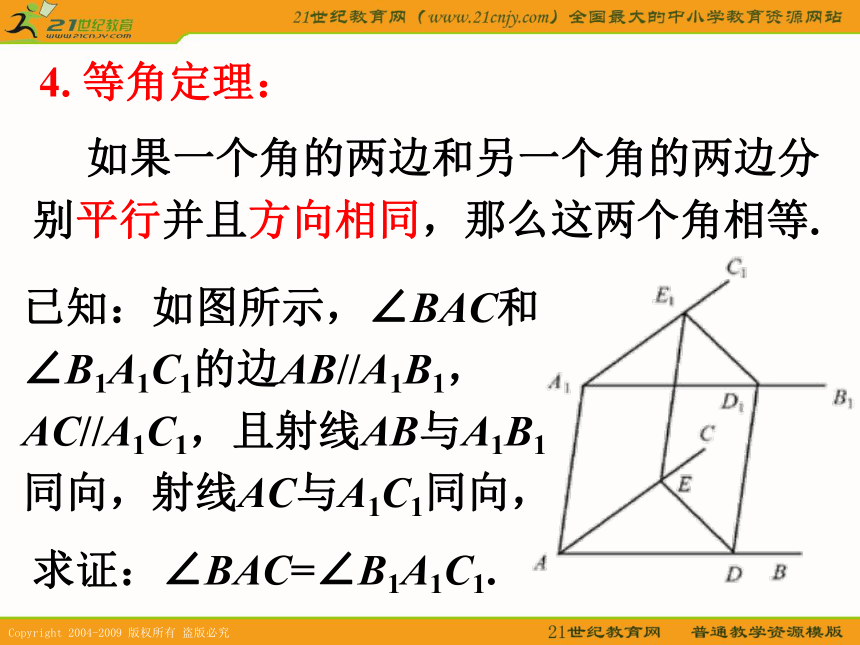
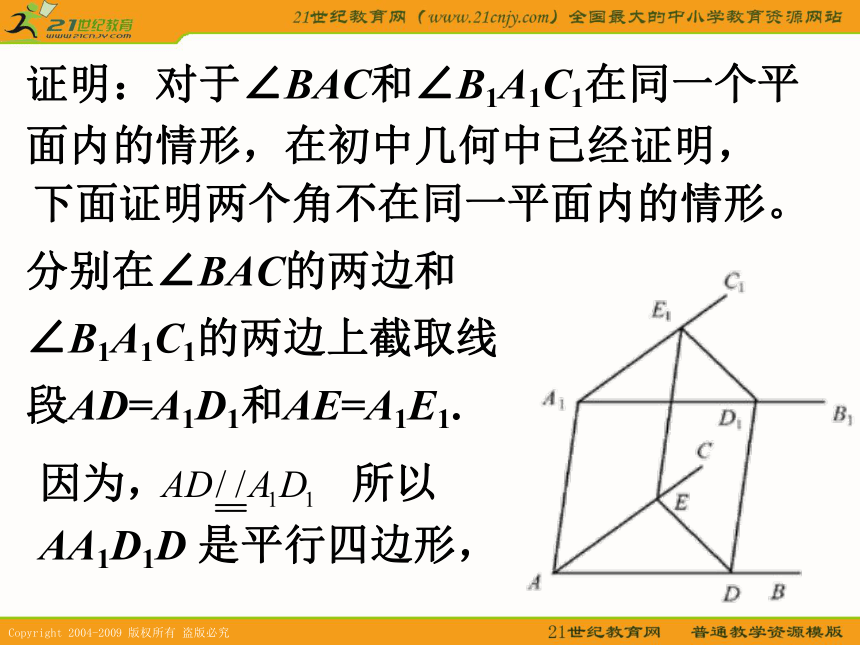
公理4主要用来证明两条直线平行,它是证明两直线平行的重要依据. 4. 等角定理: 如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.已知:如图所示,∠BAC和∠B1A1C1的边AB//A1B1,AC//A1C1,且射线AB与A1B1同向,射线AC与A1C1同向,求证:∠BAC=∠B1A1C1.证明:对于∠BAC和∠B1A1C1在同一个平面内的情形,在初中几何中已经证明, 下面证明两个角不在同一平面内的情形。 分别在∠BAC的两边和∠B1A1C1的两边上截取线段AD=A1D1和AE=A1E1. 因为, 所以AA1D1D 是平行四边形, 所以同理可得 所以DD1E1E是平行四边形。 在△ADE和△A1D1E1中. AD=A1D1,AE=A1E1,DE=D1E1, 于是△ADE≌△A1D1E1, 所以∠BAC=∠B1A1C1.5. 空间四边形的有关概念:(1)顺次连结不共面的四点A、B、C、D所构成的图形,叫做空间四边形;
(2)四个点中的各个点叫做空间四边形的顶点;
(3)所连结的相邻顶点间的线段叫做空间四边形的边;
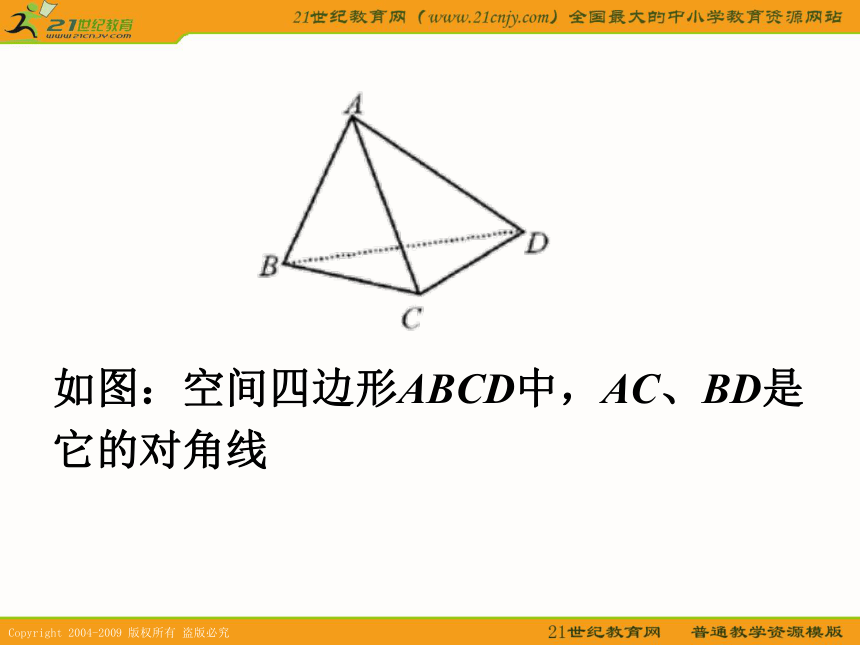
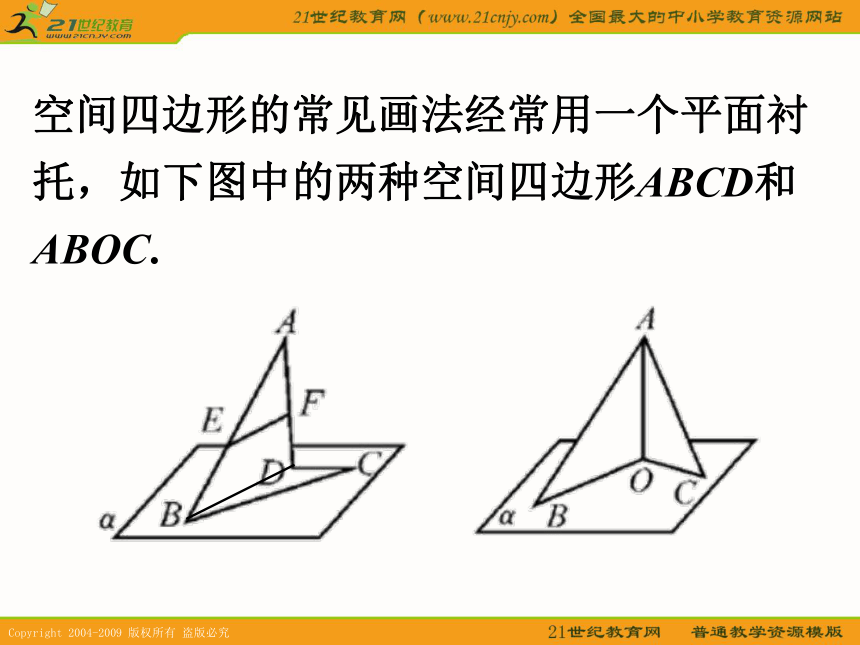
(4)连结不相邻的顶点的线段叫做空间四边形的对角线。如图:空间四边形ABCD中,AC、BD是它的对角线 空间四边形的常见画法经常用一个平面衬托,如下图中的两种空间四边形ABCD和ABOC. 6. 异面直线所成的角:已知两条异面直线a、b,经过空间任意一点O作直线a’//a,b’//b,由于a’、b’所成的角的大小与点O的选择无关,我们就把a’与b’所成的锐角或直角叫做异面直线所成的角. 若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 空间两条直线的位置关系有三种:例1.已知:如图,空间四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形。证明:在△ABD中,因为E,H分别是AB,AD的中点,所以EH//BD,EH= BD,同理,FG//BD,FG= BD,所以EH//FG,EH=FG,所以四边形EFGH是平行四边形。例2.如图:在长方体ABCD-A1B1C1D1中,已知E,F分别是AB , BC 的中点,
求证:EF∥A1C1.证明:连结AC.
在△ABC中, E, F分别是AB, BC 的中点.
所以 EF ∥ AC又因为 AA1∥BB1 且 AA1 = BB1
BB1∥CC1 且 BB1 = CC1所以 AA1∥CC1 且 AA1∥CC1 即四边形AA1C1C是平行四边形所以AC∥A1C1从而 EF∥A1C1.例3. 如图,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD, A1D1的中点.
求证:∠C1E1B1 = ∠CEB.分析:设法证明E1C1∥EC, E1B1∥EB.(1) 下列结论正确的是( )
A.若两个角相等,则这两个角的两边分别平行
B.空间四边形的四个顶点可以在一个平面内
C.空间四边形的两条对角线可以相交
D.空间四边形的两条对角线不相交D练习 题 (2) 下面三个命题, 其中正确的个数是( )
①三条相互平行的直线必共面;
②两组对边分别相等的四边形是平行四边形;
③若四边形有一组对角都是直角,则这个四边形是圆的内接四边形
A. 1个 B. 2个
C. 3个 D. 一个也不正确D(4)若空间四边形的对角线相等,则以它的四条边的中点为顶点的四边形是( )
A.空间四边形 B.菱形
C.正方形 D.梯形(3).空间两个角α、β, α与β的两边对应平行, 且α=600, 则β等( )
A. 60° B. 120°
C. 30° D. 60°或120°DB 5. 设AA1是正方体的一条棱,这个正方体中与AA1 平行的棱共有___条.3C7.如图,已知 AA1, BB1, CC1 ,不共面
且AA1∥BB1, BB1∥CC1 ,AA1=BB1, BB1= CC1.
求证:△ABC ≌ △A1B1C1.
公理4主要用来证明两条直线平行,它是证明两直线平行的重要依据. 4. 等角定理: 如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.已知:如图所示,∠BAC和∠B1A1C1的边AB//A1B1,AC//A1C1,且射线AB与A1B1同向,射线AC与A1C1同向,求证:∠BAC=∠B1A1C1.证明:对于∠BAC和∠B1A1C1在同一个平面内的情形,在初中几何中已经证明, 下面证明两个角不在同一平面内的情形。 分别在∠BAC的两边和∠B1A1C1的两边上截取线段AD=A1D1和AE=A1E1. 因为, 所以AA1D1D 是平行四边形, 所以同理可得 所以DD1E1E是平行四边形。 在△ADE和△A1D1E1中. AD=A1D1,AE=A1E1,DE=D1E1, 于是△ADE≌△A1D1E1, 所以∠BAC=∠B1A1C1.5. 空间四边形的有关概念:(1)顺次连结不共面的四点A、B、C、D所构成的图形,叫做空间四边形;
(2)四个点中的各个点叫做空间四边形的顶点;
(3)所连结的相邻顶点间的线段叫做空间四边形的边;
(4)连结不相邻的顶点的线段叫做空间四边形的对角线。如图:空间四边形ABCD中,AC、BD是它的对角线 空间四边形的常见画法经常用一个平面衬托,如下图中的两种空间四边形ABCD和ABOC. 6. 异面直线所成的角:已知两条异面直线a、b,经过空间任意一点O作直线a’//a,b’//b,由于a’、b’所成的角的大小与点O的选择无关,我们就把a’与b’所成的锐角或直角叫做异面直线所成的角. 若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 空间两条直线的位置关系有三种:例1.已知:如图,空间四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形。证明:在△ABD中,因为E,H分别是AB,AD的中点,所以EH//BD,EH= BD,同理,FG//BD,FG= BD,所以EH//FG,EH=FG,所以四边形EFGH是平行四边形。例2.如图:在长方体ABCD-A1B1C1D1中,已知E,F分别是AB , BC 的中点,
求证:EF∥A1C1.证明:连结AC.
在△ABC中, E, F分别是AB, BC 的中点.
所以 EF ∥ AC又因为 AA1∥BB1 且 AA1 = BB1
BB1∥CC1 且 BB1 = CC1所以 AA1∥CC1 且 AA1∥CC1 即四边形AA1C1C是平行四边形所以AC∥A1C1从而 EF∥A1C1.例3. 如图,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD, A1D1的中点.
求证:∠C1E1B1 = ∠CEB.分析:设法证明E1C1∥EC, E1B1∥EB.(1) 下列结论正确的是( )
A.若两个角相等,则这两个角的两边分别平行
B.空间四边形的四个顶点可以在一个平面内
C.空间四边形的两条对角线可以相交
D.空间四边形的两条对角线不相交D练习 题 (2) 下面三个命题, 其中正确的个数是( )
①三条相互平行的直线必共面;
②两组对边分别相等的四边形是平行四边形;
③若四边形有一组对角都是直角,则这个四边形是圆的内接四边形
A. 1个 B. 2个
C. 3个 D. 一个也不正确D(4)若空间四边形的对角线相等,则以它的四条边的中点为顶点的四边形是( )
A.空间四边形 B.菱形
C.正方形 D.梯形(3).空间两个角α、β, α与β的两边对应平行, 且α=600, 则β等( )
A. 60° B. 120°
C. 30° D. 60°或120°DB 5. 设AA1是正方体的一条棱,这个正方体中与AA1 平行的棱共有___条.3C7.如图,已知 AA1, BB1, CC1 ,不共面
且AA1∥BB1, BB1∥CC1 ,AA1=BB1, BB1= CC1.
求证:△ABC ≌ △A1B1C1.
