数学:1.2.2《空间中的平行关系》课件(新人教b版必修2)
文档属性
| 名称 | 数学:1.2.2《空间中的平行关系》课件(新人教b版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-28 00:00:00 | ||
图片预览






文档简介
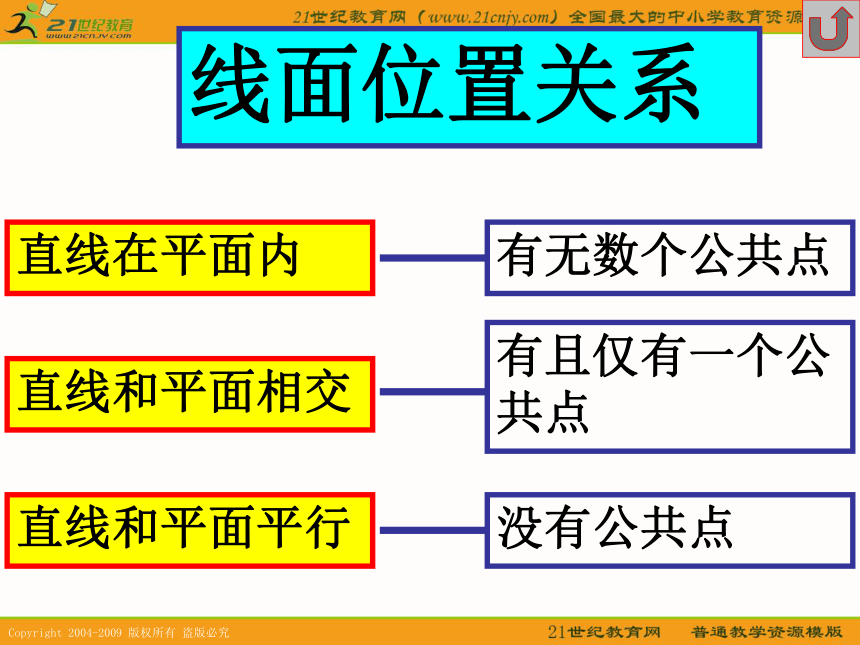
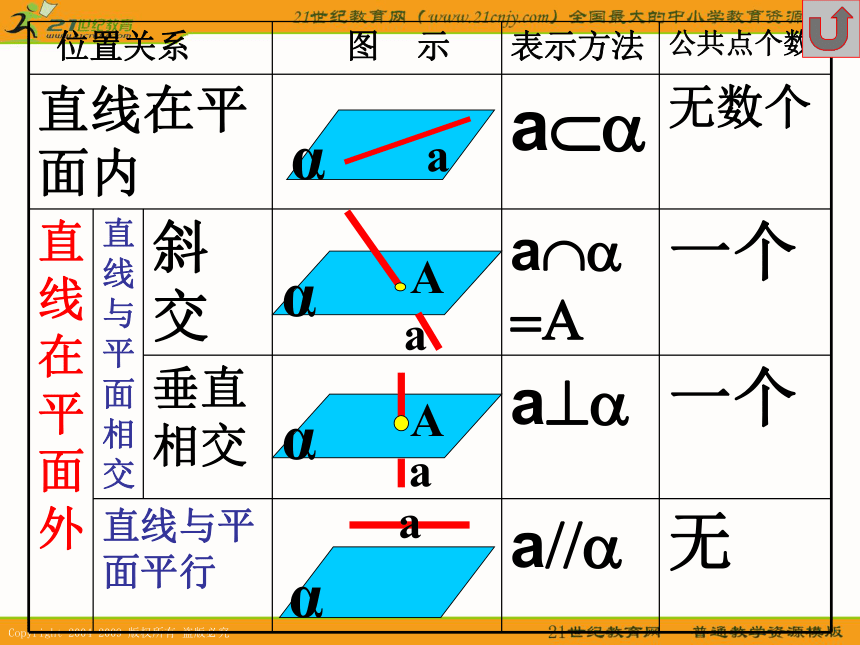
课件34张PPT。空间中的平行关系直线和平面的位置关系直线和平面的平行关系平面和平面的平行关系平面和平面的位置关系直线在平面内直线和平面相交直线和平面平行线面位置关系有无数个公共点有且仅有一个公共点没有公共点αaαaαAAaαa平行于同一平面的二直线的位置关系是 ( )(A) 一定平行(B) 平行或相交(C) 相交(D) 平行,相交,异面D1
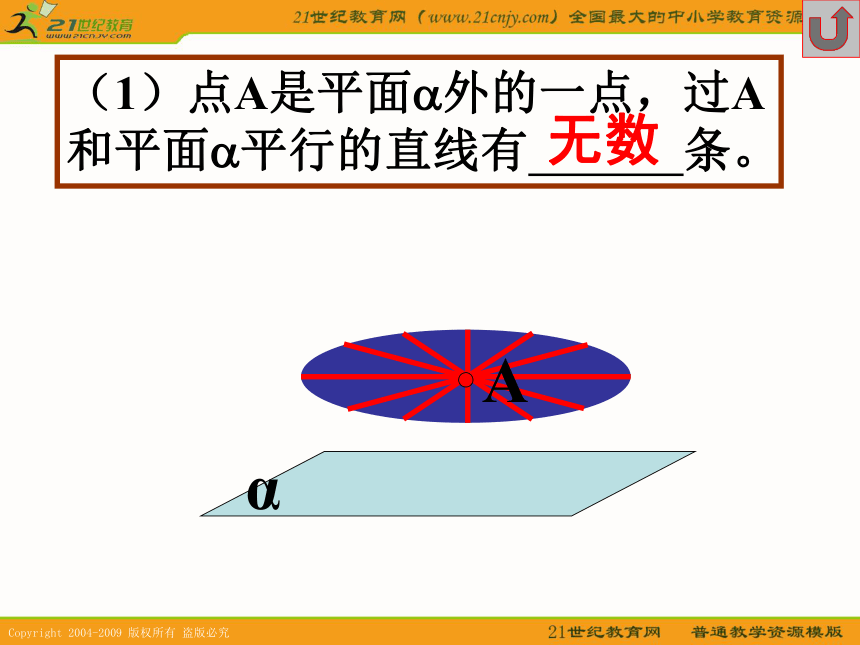
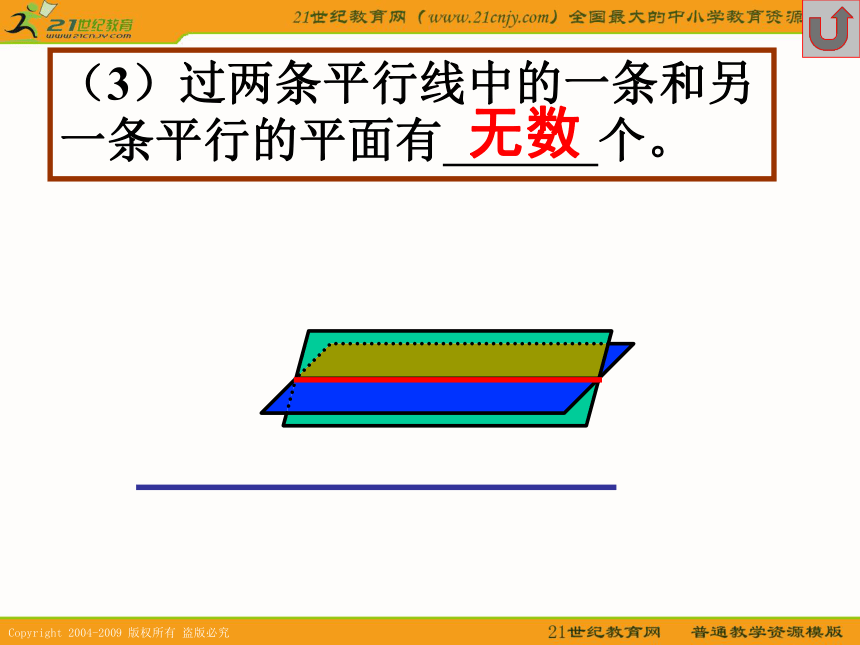
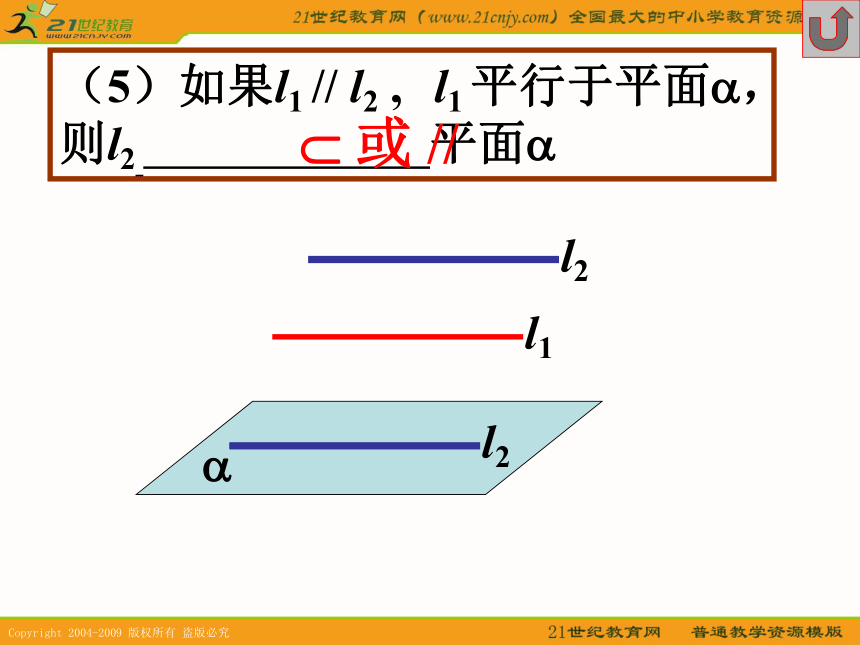
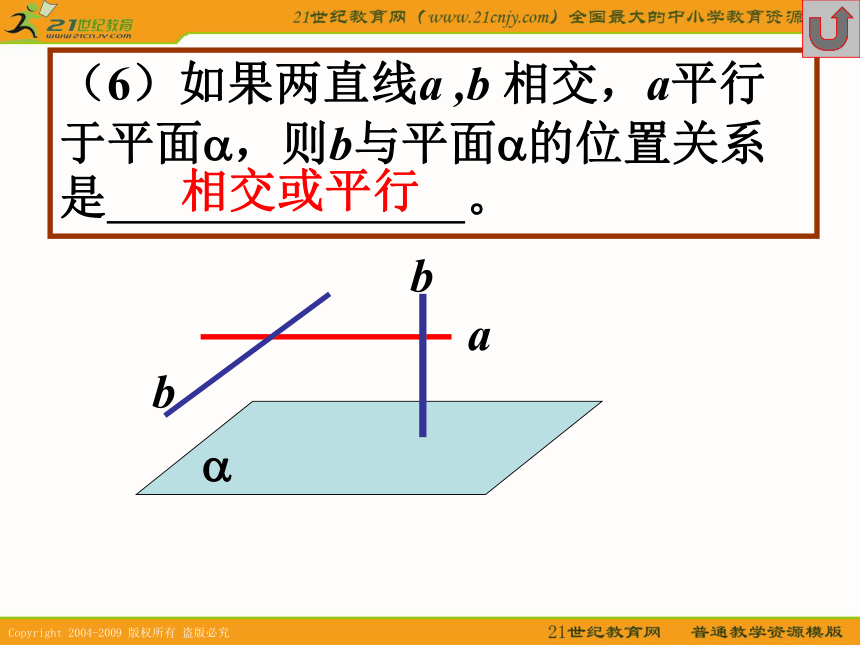
2(1)点A是平面?外的一点,过A和平面?平行的直线有 条。α无数(2)点A是直线l 外的一点,过A和直线l 平行的平面有 个。无数(3)过两条平行线中的一条和另一条平行的平面有 个。无数(4)过两条异面直线中的一条和另一条平行的平面有 个。且仅有一(5)如果l1 // l2 , l1 平行于平面?, 则l2 平面?l1?? 或 //(6)如果两直线a ,b 相交,a平行于平面?,则b与平面?的位置关系是 。a?相交或平行线面平行的判定(1) 定义——直线与平面没有公共点(2) 定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。线面平行判定定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。已知:a??? b??? a//b求证:a//?ab?(1) a,b确定平面?,???=b(2) 假设a与?不平行则a与?有公共点P则P? ???=b(3) 这与已知a//b矛盾(4) ∴a // ??如图,空间四面体P-ABC, M,N分别是面PCA和面PBC的重心 求证:MN//面BCAP∵MN// EF∴ MN //面BCA线线平行线面平行如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵MN // GH∴ MN //面BCE线线平行线面平行如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵△AFN∽ △BNH∴ AN/NH=FN/BN∴ AN/NH=AM/MC∴ MN//CH∴ MN //面BCE在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE∵DB1 // EF∴ DB1 //面A1C1E线线平行线面平行在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1BB1O(1)如果一条直线与一个平面平行,则这条直线与这个平面无公共点(2)如果一条直线与一个平面平行,则这条直线与这个平面内的直线成异面直线或平行直线(3)如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,则这条直线与交线平行。已知:a//?,a??, ? ? ?=b求证:a//b? ? ?=bb ? ?a //?a ? b=?a//b如果平面外的两条平行线中的一条与这个平面平行,则另一条直线与这个平面也平行abc如果一条直线和两个相交平面都平行,则这条直线与它们的交线平行a??l已知:a // ?, a// ? ,? ? ?=l求证:a // labABOMNP如图,a,b是异面直线,O为AB的中点,过点O作平面?与两异面直线a,b都平行MN交平面于点P,求证:MP=PN?l3、4一、两个平面平行的判定方法1、两个平面没有公共点2、一个平面内有两条相交
直线都平行于另一个平面3、都垂直于同一条直线的
两个平面两个平面平行二、两个平面平行的性质判断下列命题是否正确?1、平行于同一直线的两平面平行2、垂直于同一直线的两平面平行3、与同一直线成等角的两平面平行4、垂直于同一平面的两平面平行5、若α∥β,则平面α内任一直线a ∥β例题、如图,在正方体
ABCD-A1B1C1D1 中,
求证:面AB1D1∥面BDC1证明:B1D1∩AB1=B1面AB1D1∥
面BDC1线∥线线∥面面∥面证法2:A1C⊥BDBD∩BC1=BA1C⊥面BDC1面AB1D1
∥面BDC1变形1:如图,在正方体
ABCD-A1B1C1D1 中,
E,F,G分别为A1D1, A1B1,
A1A的中点
求证:面EFG∥面BDC1变形2:若O为BD上的点
求证:OC1 ∥面EFG
O面∥面 由上知
面EFG∥面BDC1线∥面OC1 ∥面EFG变形3:如图,在正方体
ABCD-A1B1C1D1 中,
E,F,M,N分别为A1B1,
A1D1, B1C1, C1D1 的
中点求证:面AEF∥面BDMN
小结: 线
平行
线 线
平行
面 面
平行
面线面平行判定线面平行性质面面平行判定面面平行性质三种平行关系的转化已知:四面体A-BCD,E,F,G分别为AB,AC,AD的中点求证:面EFG∥面BCD练习
2(1)点A是平面?外的一点,过A和平面?平行的直线有 条。α无数(2)点A是直线l 外的一点,过A和直线l 平行的平面有 个。无数(3)过两条平行线中的一条和另一条平行的平面有 个。无数(4)过两条异面直线中的一条和另一条平行的平面有 个。且仅有一(5)如果l1 // l2 , l1 平行于平面?, 则l2 平面?l1?? 或 //(6)如果两直线a ,b 相交,a平行于平面?,则b与平面?的位置关系是 。a?相交或平行线面平行的判定(1) 定义——直线与平面没有公共点(2) 定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。线面平行判定定理——如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。已知:a??? b??? a//b求证:a//?ab?(1) a,b确定平面?,???=b(2) 假设a与?不平行则a与?有公共点P则P? ???=b(3) 这与已知a//b矛盾(4) ∴a // ??如图,空间四面体P-ABC, M,N分别是面PCA和面PBC的重心 求证:MN//面BCAP∵MN// EF∴ MN //面BCA线线平行线面平行如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵MN // GH∴ MN //面BCE线线平行线面平行如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵△AFN∽ △BNH∴ AN/NH=FN/BN∴ AN/NH=AM/MC∴ MN//CH∴ MN //面BCE在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE∵DB1 // EF∴ DB1 //面A1C1E线线平行线面平行在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1BB1O(1)如果一条直线与一个平面平行,则这条直线与这个平面无公共点(2)如果一条直线与一个平面平行,则这条直线与这个平面内的直线成异面直线或平行直线(3)如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,则这条直线与交线平行。已知:a//?,a??, ? ? ?=b求证:a//b? ? ?=bb ? ?a //?a ? b=?a//b如果平面外的两条平行线中的一条与这个平面平行,则另一条直线与这个平面也平行abc如果一条直线和两个相交平面都平行,则这条直线与它们的交线平行a??l已知:a // ?, a// ? ,? ? ?=l求证:a // labABOMNP如图,a,b是异面直线,O为AB的中点,过点O作平面?与两异面直线a,b都平行MN交平面于点P,求证:MP=PN?l3、4一、两个平面平行的判定方法1、两个平面没有公共点2、一个平面内有两条相交
直线都平行于另一个平面3、都垂直于同一条直线的
两个平面两个平面平行二、两个平面平行的性质判断下列命题是否正确?1、平行于同一直线的两平面平行2、垂直于同一直线的两平面平行3、与同一直线成等角的两平面平行4、垂直于同一平面的两平面平行5、若α∥β,则平面α内任一直线a ∥β例题、如图,在正方体
ABCD-A1B1C1D1 中,
求证:面AB1D1∥面BDC1证明:B1D1∩AB1=B1面AB1D1∥
面BDC1线∥线线∥面面∥面证法2:A1C⊥BDBD∩BC1=BA1C⊥面BDC1面AB1D1
∥面BDC1变形1:如图,在正方体
ABCD-A1B1C1D1 中,
E,F,G分别为A1D1, A1B1,
A1A的中点
求证:面EFG∥面BDC1变形2:若O为BD上的点
求证:OC1 ∥面EFG
O面∥面 由上知
面EFG∥面BDC1线∥面OC1 ∥面EFG变形3:如图,在正方体
ABCD-A1B1C1D1 中,
E,F,M,N分别为A1B1,
A1D1, B1C1, C1D1 的
中点求证:面AEF∥面BDMN
小结: 线
平行
线 线
平行
面 面
平行
面线面平行判定线面平行性质面面平行判定面面平行性质三种平行关系的转化已知:四面体A-BCD,E,F,G分别为AB,AC,AD的中点求证:面EFG∥面BCD练习
