1.2 整式的乘法(第1课时 单项式与单项式相乘)课件(共27张PPT) 2024-2025学年北师大版七年级数学下册
文档属性
| 名称 | 1.2 整式的乘法(第1课时 单项式与单项式相乘)课件(共27张PPT) 2024-2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-10 14:06:02 | ||
图片预览








文档简介
(共27张PPT)
北师大版(2024)七年级数学下册 第一章 整式的乘除
1.2 整式的乘法
第1课时 单项式与单项式相乘
目录
学习目标
01
情景导入
02
新知探究
03
课本例题
04
05
课本练习
06
分层练习
08
07
课本习题
课堂小结
学习目标
1. 掌握单项式与单项式相乘的运算法则.(重点)
2. 能够灵活地进行单项式与单项式相乘的运算.(难点)
情景导入
1.同底数幂的乘法:
2.幂的乘方:
3.积的乘方:
aman=am+n
(am)n=amn
(ab)n=anbn
4.同底数幂的除法:
前面学习了哪些幂的运算 运算法则分别是什么
m,n都是正整数
am÷an=am+n
新知探究
一个长方形操场被划分成四个不同的小长方形活动区域,各边的长度如图所示。如何计算整个操场的面积 你是怎样想的 与同伴进行交流。
A
B
C
D
2b
3a
a
3b
可以直接计算整个长方形的面积,也可以分别求出A,B,C,D区域的面积,再相加即可.
尝试思考
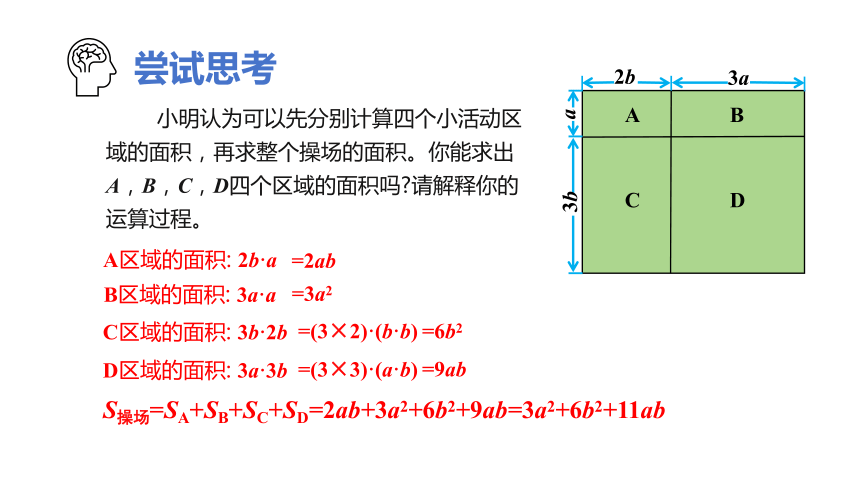
小明认为可以先分别计算四个小活动区域的面积,再求整个操场的面积。你能求出A,B,C,D四个区域的面积吗 请解释你的运算过程。
A
B
C
D
2b
3a
a
3b
A区域的面积: 2b·a
B区域的面积: 3a·a
C区域的面积: 3b·2b
D区域的面积: 3a·3b
=2ab
=3a2
=(3×2)·(b·b)
=6b2
=(3×3)·(a·b)
=9ab
S操场=SA+SB+SC+SD=2ab+3a2+6b2+9ab=3a2+6b2+11ab
操作交流
(1)你能计算abc·b2c,3x2y·2xy3及5a2b2·(-2ab)吗?
(2)一般地,如何进行单项式乘单项式的运算?与同伴进行交流.
abc·b2c=a·(b·b2)·(c·c)=ab3c2.
3x2y·2xy3=(3×2)·(x2·x)·(y·y3)=6x3y4.
5a2b2·(-2ab)=[5×(-2)]·(a2·a)·(b2·b)=-10a3b3.
单项式与单项式相乘
有理数的乘法与同底数幂的乘法
乘法交换律和结合律
转化
知识归纳
单项式与单项式的乘法法则:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
简记为“两相乘,一不变”
单项式乘以单项式的结果仍是单项式.
注意:
①系数相乘;
②相同字母的幂相乘;
③其余字母连同它的指数不变,作为积的因式。
单项式乘单项式的运算法则的推广:
对于三个或三个以上的单项式相乘,单项式乘单项式的运算法则同样适用.
例题讲解
课本例题 例1 计算:
(1)2xy2·xy;
(2)–2a2b3·(–3a);
(3)7xy2z·(2xyz)2;
解:(1)2xy2·xy = (2×)·(xx) ·(y2y) = x2y3 ;
(2)–2a2b3·(–3a) = [(–2)×(–3)]·(a2a)·b3 = 6a3b3;
(4)(–3ab)· a2c·(–2abc3) 。
例题讲解
课本例题 例1 计算:
(1)2xy2·xy;
(2)–2a2b3·(–3a);
(3)7xy2z·(2xyz)2;
(4)(–3ab)· a2c·(–2abc3) 。
解:(3)7xy2z·(2xyz)2=7xy2z·4x2y2z2=(7×4)·(xx2)·(y2y2)·(zz2)
=28x3y4z3;
(4)(–3ab)· a2c·(–2abc3)=[(–3)××(–2)]·(aa2a)·(bb)·(cc3)
= 2a4b2c4。
例题讲解
补充例题 例1
已知 (–2axby2c)·(3xb-1y) = 12x11y7,求 a + b + c 的值。
解:因为 (– 2axby2c)·(3xb-1y) = 12x11y7,
所以 – 6ax2b-1y2c+1 = 12x11y7,
所以 – 6a = 12,2b – 1 = 11,2c + 1 = 7,
所以 a = – 2,b = 6,c = 3,
所以 a + b + c = – 2 + 6 + 3 = 7。
例题讲解
补充例题 例2
已知一个长方体包装箱,长为3a m,宽为2b m,高为ab m.
(1)求这个包装箱的体积;
(2)如果给这个包装箱的外表面都喷上油漆,那么共需喷多少平方米的油漆
解:因为3a·2b·ab=6a2b2(m3),
所以这个包装箱的体积为6a2b2 m3.
解:包装箱的表面积为2(3a·2b+3a·ab+2b·ab)=(12ab+6a2b+4ab2)m2,
所以共需喷(12ab+6a2b+4ab2)m2的油漆.
观察思考
新课讲授
如图,一幅边长为 a m 的正方形风景画,上下各留有 a m 的空白区域作装饰,中间画面的面积是多少平方米
解:a·(a- a-a)
=a·a
=a2 (m2)
答:中间画面的面积是a2平方米。
随堂练习
(1)5x3·2x2y; (2)–3ab·(–4b2) ; (3)3ab·2a;
(4)yz·2y2z2 ;
(5)(2x2y)3·(–4xy2); (6)a3b·6a5b2c·(–ac2)2。
1.计算:
解:(1)5x3·2x2y = (5×2)·(x3x2)·y=10x5y;
(2)–3ab·(–4b2)=[(–3)×(–4)]·a·(bb2)=12ab3;
(3) 3ab·2a = (3×2)·(aa)·b=6a2b;
(4) yz·2y2z2 =2·(yy2)·(zz2)=2y3z3;
(5)(2x2y)3·(–4xy2)=(8x6y3) ·(–4xy2)=[8×(–4)]·(x6x)·(y3y2)= –32x7y5;
(6)a3b·6a5b2c·(–ac2)2=a3b·6a5b2c·(a2c4)=(×6)·(a3a5a2)·(bb2)·(cc4)
=2a10b3c5。
分层练习
基础题
1.填空: 。
5
3
2.[2024运城期中] 下列计算中,正确的是( )
A
A. B.
C. D.
3. [2024益阳模拟] 化简 的结果是( )
A
A. B. C. D.
4. 如果,那么 内应填的代数式是( )
C
A. B. C. D.
5. 下列运算正确的是( )
D
A. B.
C. D.
6.如果单项式与 之和仍是单项式,那么这两个
单项式的积为( )
A
A. B. C. D.
7. [2024青岛模拟] 已知单项式与的积为 ,
那么 ( )
C
A. 11 B. 5 C. 1 D.
8. 已知两个单项式的积是 ,则这两个单项式可以是
_____________________________.(写出一对即可)
和(答案不唯一)
9.计算:
(1) ;
解:原式 。
(2) ;
原式 。
(3) 。
原式
。
10.计算:
(1) ;
【解】原式 .
(2) ;
原式 .
(3) .
原式 .
11.一个三角形的底边长为,底边上的高的长为 ,则它的面积为
____。
12.某同学家的住房结构如图所示,他家打算把卧室和客厅铺上地板,请
你帮他算一算,至少需要地板的面积是______。
综合应用题
13.阅读下列运算过程,回答问题。
①
②
。 ③
(1)上述解答过程有错误,从第____步开始错误,原因是
______________________________;
①
弄错乘方运算和乘法运算的顺序
(2)请写出正确的运算过程。
解:正确的运算过程如下:
。
14. 某市环保局欲将一个长为 ,宽为,高为 的
长方体废水池中的满池废水注入正方体贮水池净化.
(1)这些废水能否刚好装满一个正方体贮水池?____.
(请填“能”或“不能”)
(2)若能,则该正方体贮水池的棱长为_____ .
能
15.[2024寿光期中] 先化简,再求值:
,其中 ,
, 。
解:
。
当,, 时,
原式 。
16. 已知单项式与 的积与是同类项,
求, 的值.
【解】 .
因为与 是同类项,
所以,,解得, .
创新拓展题
17.小明计算一道整式乘法题: 由于小明将第一个
单项式中的抄成了 ,将第二个单项式中的抄成了,
结果得到 .
(1)根据上述信息,分别计算出, 的值;
【解】因为,
所以, .解得, .
(2)请你计算出这道整式乘法题的正确答案.
【解】因为, ,
所以 .
课堂小结
单项式与
单项式相乘
转化为同底数幂的运算
注意
实质
(1)不要出现漏乘现象;
(2)有乘方运算,先算乘方,再算单项式相乘.
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
法则
北师大版(2024)七年级数学下册 第一章 整式的乘除
1.2 整式的乘法
第1课时 单项式与单项式相乘
目录
学习目标
01
情景导入
02
新知探究
03
课本例题
04
05
课本练习
06
分层练习
08
07
课本习题
课堂小结
学习目标
1. 掌握单项式与单项式相乘的运算法则.(重点)
2. 能够灵活地进行单项式与单项式相乘的运算.(难点)
情景导入
1.同底数幂的乘法:
2.幂的乘方:
3.积的乘方:
aman=am+n
(am)n=amn
(ab)n=anbn
4.同底数幂的除法:
前面学习了哪些幂的运算 运算法则分别是什么
m,n都是正整数
am÷an=am+n
新知探究
一个长方形操场被划分成四个不同的小长方形活动区域,各边的长度如图所示。如何计算整个操场的面积 你是怎样想的 与同伴进行交流。
A
B
C
D
2b
3a
a
3b
可以直接计算整个长方形的面积,也可以分别求出A,B,C,D区域的面积,再相加即可.
尝试思考
小明认为可以先分别计算四个小活动区域的面积,再求整个操场的面积。你能求出A,B,C,D四个区域的面积吗 请解释你的运算过程。
A
B
C
D
2b
3a
a
3b
A区域的面积: 2b·a
B区域的面积: 3a·a
C区域的面积: 3b·2b
D区域的面积: 3a·3b
=2ab
=3a2
=(3×2)·(b·b)
=6b2
=(3×3)·(a·b)
=9ab
S操场=SA+SB+SC+SD=2ab+3a2+6b2+9ab=3a2+6b2+11ab
操作交流
(1)你能计算abc·b2c,3x2y·2xy3及5a2b2·(-2ab)吗?
(2)一般地,如何进行单项式乘单项式的运算?与同伴进行交流.
abc·b2c=a·(b·b2)·(c·c)=ab3c2.
3x2y·2xy3=(3×2)·(x2·x)·(y·y3)=6x3y4.
5a2b2·(-2ab)=[5×(-2)]·(a2·a)·(b2·b)=-10a3b3.
单项式与单项式相乘
有理数的乘法与同底数幂的乘法
乘法交换律和结合律
转化
知识归纳
单项式与单项式的乘法法则:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
简记为“两相乘,一不变”
单项式乘以单项式的结果仍是单项式.
注意:
①系数相乘;
②相同字母的幂相乘;
③其余字母连同它的指数不变,作为积的因式。
单项式乘单项式的运算法则的推广:
对于三个或三个以上的单项式相乘,单项式乘单项式的运算法则同样适用.
例题讲解
课本例题 例1 计算:
(1)2xy2·xy;
(2)–2a2b3·(–3a);
(3)7xy2z·(2xyz)2;
解:(1)2xy2·xy = (2×)·(xx) ·(y2y) = x2y3 ;
(2)–2a2b3·(–3a) = [(–2)×(–3)]·(a2a)·b3 = 6a3b3;
(4)(–3ab)· a2c·(–2abc3) 。
例题讲解
课本例题 例1 计算:
(1)2xy2·xy;
(2)–2a2b3·(–3a);
(3)7xy2z·(2xyz)2;
(4)(–3ab)· a2c·(–2abc3) 。
解:(3)7xy2z·(2xyz)2=7xy2z·4x2y2z2=(7×4)·(xx2)·(y2y2)·(zz2)
=28x3y4z3;
(4)(–3ab)· a2c·(–2abc3)=[(–3)××(–2)]·(aa2a)·(bb)·(cc3)
= 2a4b2c4。
例题讲解
补充例题 例1
已知 (–2axby2c)·(3xb-1y) = 12x11y7,求 a + b + c 的值。
解:因为 (– 2axby2c)·(3xb-1y) = 12x11y7,
所以 – 6ax2b-1y2c+1 = 12x11y7,
所以 – 6a = 12,2b – 1 = 11,2c + 1 = 7,
所以 a = – 2,b = 6,c = 3,
所以 a + b + c = – 2 + 6 + 3 = 7。
例题讲解
补充例题 例2
已知一个长方体包装箱,长为3a m,宽为2b m,高为ab m.
(1)求这个包装箱的体积;
(2)如果给这个包装箱的外表面都喷上油漆,那么共需喷多少平方米的油漆
解:因为3a·2b·ab=6a2b2(m3),
所以这个包装箱的体积为6a2b2 m3.
解:包装箱的表面积为2(3a·2b+3a·ab+2b·ab)=(12ab+6a2b+4ab2)m2,
所以共需喷(12ab+6a2b+4ab2)m2的油漆.
观察思考
新课讲授
如图,一幅边长为 a m 的正方形风景画,上下各留有 a m 的空白区域作装饰,中间画面的面积是多少平方米
解:a·(a- a-a)
=a·a
=a2 (m2)
答:中间画面的面积是a2平方米。
随堂练习
(1)5x3·2x2y; (2)–3ab·(–4b2) ; (3)3ab·2a;
(4)yz·2y2z2 ;
(5)(2x2y)3·(–4xy2); (6)a3b·6a5b2c·(–ac2)2。
1.计算:
解:(1)5x3·2x2y = (5×2)·(x3x2)·y=10x5y;
(2)–3ab·(–4b2)=[(–3)×(–4)]·a·(bb2)=12ab3;
(3) 3ab·2a = (3×2)·(aa)·b=6a2b;
(4) yz·2y2z2 =2·(yy2)·(zz2)=2y3z3;
(5)(2x2y)3·(–4xy2)=(8x6y3) ·(–4xy2)=[8×(–4)]·(x6x)·(y3y2)= –32x7y5;
(6)a3b·6a5b2c·(–ac2)2=a3b·6a5b2c·(a2c4)=(×6)·(a3a5a2)·(bb2)·(cc4)
=2a10b3c5。
分层练习
基础题
1.填空: 。
5
3
2.[2024运城期中] 下列计算中,正确的是( )
A
A. B.
C. D.
3. [2024益阳模拟] 化简 的结果是( )
A
A. B. C. D.
4. 如果,那么 内应填的代数式是( )
C
A. B. C. D.
5. 下列运算正确的是( )
D
A. B.
C. D.
6.如果单项式与 之和仍是单项式,那么这两个
单项式的积为( )
A
A. B. C. D.
7. [2024青岛模拟] 已知单项式与的积为 ,
那么 ( )
C
A. 11 B. 5 C. 1 D.
8. 已知两个单项式的积是 ,则这两个单项式可以是
_____________________________.(写出一对即可)
和(答案不唯一)
9.计算:
(1) ;
解:原式 。
(2) ;
原式 。
(3) 。
原式
。
10.计算:
(1) ;
【解】原式 .
(2) ;
原式 .
(3) .
原式 .
11.一个三角形的底边长为,底边上的高的长为 ,则它的面积为
____。
12.某同学家的住房结构如图所示,他家打算把卧室和客厅铺上地板,请
你帮他算一算,至少需要地板的面积是______。
综合应用题
13.阅读下列运算过程,回答问题。
①
②
。 ③
(1)上述解答过程有错误,从第____步开始错误,原因是
______________________________;
①
弄错乘方运算和乘法运算的顺序
(2)请写出正确的运算过程。
解:正确的运算过程如下:
。
14. 某市环保局欲将一个长为 ,宽为,高为 的
长方体废水池中的满池废水注入正方体贮水池净化.
(1)这些废水能否刚好装满一个正方体贮水池?____.
(请填“能”或“不能”)
(2)若能,则该正方体贮水池的棱长为_____ .
能
15.[2024寿光期中] 先化简,再求值:
,其中 ,
, 。
解:
。
当,, 时,
原式 。
16. 已知单项式与 的积与是同类项,
求, 的值.
【解】 .
因为与 是同类项,
所以,,解得, .
创新拓展题
17.小明计算一道整式乘法题: 由于小明将第一个
单项式中的抄成了 ,将第二个单项式中的抄成了,
结果得到 .
(1)根据上述信息,分别计算出, 的值;
【解】因为,
所以, .解得, .
(2)请你计算出这道整式乘法题的正确答案.
【解】因为, ,
所以 .
课堂小结
单项式与
单项式相乘
转化为同底数幂的运算
注意
实质
(1)不要出现漏乘现象;
(2)有乘方运算,先算乘方,再算单项式相乘.
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
法则
同课章节目录
