7.3 同底数幂的除法 (第2课时 零指数幂与负整数指数幂)课件(共32张PPT) 2024-2025学年苏科版七年级数学下册
文档属性
| 名称 | 7.3 同底数幂的除法 (第2课时 零指数幂与负整数指数幂)课件(共32张PPT) 2024-2025学年苏科版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-10 14:12:25 | ||
图片预览











文档简介
(共32张PPT)
苏科版(2024)七年级数学下册 第七章 幂的运算
7.3 同底数幂的除法
第2课时 零指数幂与负整数指数幂
目录
学习目标
01
情景导入
02
新知探究
03
课本例题
04
05
课本练习
06
分层练习
08
07
课本习题
课堂小结
学习目标
1. 了解(a≠0,n为正整数)的规定;
2. 会计算底数为负数的负整数指数幂;
3. 在对“规定”的合理性做出解释的过程中,感受从特殊到一般、从具体到抽象的思考问题的方法.
情景导入
前面我们学习了同底数幂相除的运算性质:
同底数幂相除,底数不变,指数相减.
那么,当m=n,m<n时,还能用同底数幂的除法运算性质
am ÷an =am-n进行计算吗?
新知探究
当m=n时,由除法的意义可知1.为了使上述性质仍然成立,我们规定:
任何不等于0的数的0次幂等于1.
用符号表示为: .
于是, .
也即,当m=n时, 仍然成立.
任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数.
用符号表为:
特别地,
为了使仍然成立,我们规定:
当m在式子 中,如果令m=0,那么
规定了零指数幂、负整数指数幂的意义后,同底数幂的除法运算性质可以扩展为:
根据这样的规定,当m例题讲解
课本例题 例2 用小数或分数表示下列各数:
解:
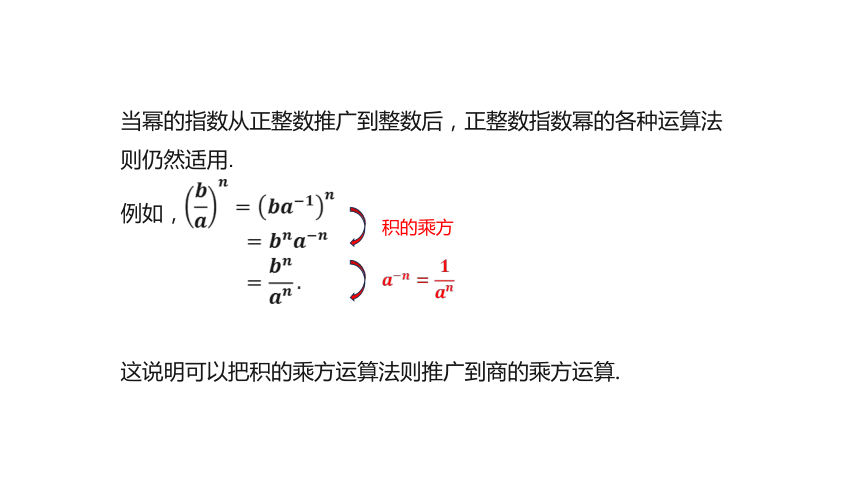
当幂的指数从正整数推广到整数后,正整数指数幂的各种运算法则仍然适用.
例如,
这说明可以把积的乘方运算法则推广到商的乘方运算.
积的乘方
例题讲解
课本例题 例3 计算
例题讲解
(4)2x=,则 x= ;
(2)当 x 时,(x+5)0有意义;
(1)(x-3)0成立的条件是 ;
补充例题 例1 填空:
x≠3
≠-5
≠-
-3
10
-4
(3)若(3x+1)-3有意义,则 x ;
(5)x-1=,则 x= ;
(6)10x=0.0001,则 x= ;
例题讲解
补充例题 例2
计算:-(3×2-4)0+(- )-4-4-2×(-)-3.
解:-(3×2-4)0+(-)-4-4-2×(-)-3
=-1+16- ×(-64)
=15+4
=19.
4-2==,(-)-3==-64
或 (-)-3 =(-4)3=-64.
课堂练习
1.用小数或分数表示下列各数:
解
2. 把下列各数写成负整数指数幂的形式:
解
3. 计算:
解
分层练习
1.若(a-2)0=1,则a的取值范围是( D )
A.a>2 B.a=2
C.a<2 D.a≠2
【点拨】
零指数幂的底数不能为0.
D
基础题
2.[2023·雅安]计算20-1的结果是( D )
A.-1 B.1
C.19 D.0
D
3.[2023·黄冈]计算:(-1)2+= .
2
4.[2024南京玄武区期末] 计算 的结果是( )
A
A.B.C.3 D.
5.下列运算正确的是( )
D
A. B.
C. D.
6.若有意义,则 的取值范围是( )
D
A. B.C.或D.且
7.[2024常州天宁区二模] 下列运算结果最大的是( )
A
A.B.C. D.
8.若(x-3)0-2(3x-6)-2有意义,则x的取值范围是( B )
A.x>3
B.x≠3且x≠2
C.x≠3或x≠2
D.x<2
B
9.[2023·永州改编]下列各式计算结果正确的是( D )
A.3x+2x=5x2 B.x6÷x2=x3
C.(2x)2=2x2 D.2-1=
【点拨】
3x+2x=5x,故选项A不正确;
x6÷x2=x4,故选项
B不正确;(2x)2=4x2,故选项C不正确;
2-1=,故选项D正确.
D
10.计算:
(1) _ _;
(2) _ _;
(3) _ ___;
(4) __;
(5) _____;
(6) __;
(7) ___;
(8) ___;
(9) __________.
1
1
11.[2023·泰州]若a≠0,则下列计算正确的是( A )
A.(-a)0=1 B.a6÷a3=a2
C.a-1=-a D.a6-a3=a3
A
易错点 对零指数幂的意义理解不透而出错
12.若x满足(x-2)x+1=1,则整数x的值为 .
-1或3或1
①x+1=0,且x-2≠0,解得x=-1;
②x-2=1,解得x=3;
③x-2=-1,且x+1为偶数,解得x=1.
综上,整数x的值为-1或3或1.
【点拨】
由题意可知分三种情况:
13.[2024苏州吴江区月考] 计算:
(1) ;
解:原式 .
(2) ;
解:原式 .
(3) ;
解:原式 .
(4) .
解:原式 .
综合应用题
14. 在物理学中,表示电流大小的单位有千安 、
安培、毫安、微安等,其中 ,
, .若某新能源电动汽车的充电电流为
,则 等于( )
D
A.B.C. D.
15.已知,,,,则, ,
, 的大小关系是( )
A
A. B.
C. D.
[解析] 点拨:因为, ,
,,所以,故选 .
16.计算:
(1)|-3|+22-(π-1)0;
(2)+(-2)3++|-2|;
(3)÷-+3-1.
【解】原式=3+4-1=6.
原式=1-8+3+2=-2.
原式=÷-1+=1-1+=.
17.(1)已知,则 ____;
(2)已知,则 ___;
(3)已知,, ,
,则 _________.
1
18.小明学习了幂的运算后做这样一道题:若,求 的值.
他解出来的结果为 ,老师说小明考虑问题不全面,聪明的你能帮
助小明解这道题吗?结果是______________.
或1或
19.定义一种新运算:,例如 .
若,则 ____.
[解析] 点拨:若,则 ,所以
.所以 .
20.[2024无锡新吴区月考] 已知,, ,
请用“ ”把它们按从小到大的顺序连接起来,并说明理由.
解:.理由:因为 ,
,, ,
所以 .
所以 .
创新拓展题
21. [新考法 类比猜想法](1)观察下列各式:
① 24÷23=24-3=21;② 24÷22=24-2=22;
③ 24÷2=24-1=23;④ 24÷20=24-0=24.
由此可猜想:
24÷2-1= ;24÷2-2= .
24-(-1)=25
24-(-2)=26
(2)上面各式表明:在am÷an=am-n中,m,n除了可以表示
正整数外,还可以表示 .
零和负整数
(3)利用上面的结论计算:
① 33÷3-7; ②÷.
【解】原式=33-(-7)=310.
原式==-.
22. 阅读下面的材料:
求 的值.
解:设 ,①
则 ,②
,得.所以原式 .
请你仿此计算:
(1) ;
解:设 ,①
则 ,②
,得 ,所以.所以原式 .
(2)( 为大于1的正整数).
解:设 ,①
则 ,②
,得,所以 .所以原式 .
课堂小结
一个性质
由特殊到一般的思考问题的方法
二个幂
同底幂的除法运算法则: am÷an=am–n(a≠0,m、n为整数)
零指数幂
a0 =1 (a≠0)
负指数幂
一个方法
同底数幂除法的运算性质
适用于一切整数指数幂
苏科版(2024)七年级数学下册 第七章 幂的运算
7.3 同底数幂的除法
第2课时 零指数幂与负整数指数幂
目录
学习目标
01
情景导入
02
新知探究
03
课本例题
04
05
课本练习
06
分层练习
08
07
课本习题
课堂小结
学习目标
1. 了解(a≠0,n为正整数)的规定;
2. 会计算底数为负数的负整数指数幂;
3. 在对“规定”的合理性做出解释的过程中,感受从特殊到一般、从具体到抽象的思考问题的方法.
情景导入
前面我们学习了同底数幂相除的运算性质:
同底数幂相除,底数不变,指数相减.
那么,当m=n,m<n时,还能用同底数幂的除法运算性质
am ÷an =am-n进行计算吗?
新知探究
当m=n时,由除法的意义可知1.为了使上述性质仍然成立,我们规定:
任何不等于0的数的0次幂等于1.
用符号表示为: .
于是, .
也即,当m=n时, 仍然成立.
任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数.
用符号表为:
特别地,
为了使仍然成立,我们规定:
当m
规定了零指数幂、负整数指数幂的意义后,同底数幂的除法运算性质可以扩展为:
根据这样的规定,当m
课本例题 例2 用小数或分数表示下列各数:
解:
当幂的指数从正整数推广到整数后,正整数指数幂的各种运算法则仍然适用.
例如,
这说明可以把积的乘方运算法则推广到商的乘方运算.
积的乘方
例题讲解
课本例题 例3 计算
例题讲解
(4)2x=,则 x= ;
(2)当 x 时,(x+5)0有意义;
(1)(x-3)0成立的条件是 ;
补充例题 例1 填空:
x≠3
≠-5
≠-
-3
10
-4
(3)若(3x+1)-3有意义,则 x ;
(5)x-1=,则 x= ;
(6)10x=0.0001,则 x= ;
例题讲解
补充例题 例2
计算:-(3×2-4)0+(- )-4-4-2×(-)-3.
解:-(3×2-4)0+(-)-4-4-2×(-)-3
=-1+16- ×(-64)
=15+4
=19.
4-2==,(-)-3==-64
或 (-)-3 =(-4)3=-64.
课堂练习
1.用小数或分数表示下列各数:
解
2. 把下列各数写成负整数指数幂的形式:
解
3. 计算:
解
分层练习
1.若(a-2)0=1,则a的取值范围是( D )
A.a>2 B.a=2
C.a<2 D.a≠2
【点拨】
零指数幂的底数不能为0.
D
基础题
2.[2023·雅安]计算20-1的结果是( D )
A.-1 B.1
C.19 D.0
D
3.[2023·黄冈]计算:(-1)2+= .
2
4.[2024南京玄武区期末] 计算 的结果是( )
A
A.B.C.3 D.
5.下列运算正确的是( )
D
A. B.
C. D.
6.若有意义,则 的取值范围是( )
D
A. B.C.或D.且
7.[2024常州天宁区二模] 下列运算结果最大的是( )
A
A.B.C. D.
8.若(x-3)0-2(3x-6)-2有意义,则x的取值范围是( B )
A.x>3
B.x≠3且x≠2
C.x≠3或x≠2
D.x<2
B
9.[2023·永州改编]下列各式计算结果正确的是( D )
A.3x+2x=5x2 B.x6÷x2=x3
C.(2x)2=2x2 D.2-1=
【点拨】
3x+2x=5x,故选项A不正确;
x6÷x2=x4,故选项
B不正确;(2x)2=4x2,故选项C不正确;
2-1=,故选项D正确.
D
10.计算:
(1) _ _;
(2) _ _;
(3) _ ___;
(4) __;
(5) _____;
(6) __;
(7) ___;
(8) ___;
(9) __________.
1
1
11.[2023·泰州]若a≠0,则下列计算正确的是( A )
A.(-a)0=1 B.a6÷a3=a2
C.a-1=-a D.a6-a3=a3
A
易错点 对零指数幂的意义理解不透而出错
12.若x满足(x-2)x+1=1,则整数x的值为 .
-1或3或1
①x+1=0,且x-2≠0,解得x=-1;
②x-2=1,解得x=3;
③x-2=-1,且x+1为偶数,解得x=1.
综上,整数x的值为-1或3或1.
【点拨】
由题意可知分三种情况:
13.[2024苏州吴江区月考] 计算:
(1) ;
解:原式 .
(2) ;
解:原式 .
(3) ;
解:原式 .
(4) .
解:原式 .
综合应用题
14. 在物理学中,表示电流大小的单位有千安 、
安培、毫安、微安等,其中 ,
, .若某新能源电动汽车的充电电流为
,则 等于( )
D
A.B.C. D.
15.已知,,,,则, ,
, 的大小关系是( )
A
A. B.
C. D.
[解析] 点拨:因为, ,
,,所以,故选 .
16.计算:
(1)|-3|+22-(π-1)0;
(2)+(-2)3++|-2|;
(3)÷-+3-1.
【解】原式=3+4-1=6.
原式=1-8+3+2=-2.
原式=÷-1+=1-1+=.
17.(1)已知,则 ____;
(2)已知,则 ___;
(3)已知,, ,
,则 _________.
1
18.小明学习了幂的运算后做这样一道题:若,求 的值.
他解出来的结果为 ,老师说小明考虑问题不全面,聪明的你能帮
助小明解这道题吗?结果是______________.
或1或
19.定义一种新运算:,例如 .
若,则 ____.
[解析] 点拨:若,则 ,所以
.所以 .
20.[2024无锡新吴区月考] 已知,, ,
请用“ ”把它们按从小到大的顺序连接起来,并说明理由.
解:.理由:因为 ,
,, ,
所以 .
所以 .
创新拓展题
21. [新考法 类比猜想法](1)观察下列各式:
① 24÷23=24-3=21;② 24÷22=24-2=22;
③ 24÷2=24-1=23;④ 24÷20=24-0=24.
由此可猜想:
24÷2-1= ;24÷2-2= .
24-(-1)=25
24-(-2)=26
(2)上面各式表明:在am÷an=am-n中,m,n除了可以表示
正整数外,还可以表示 .
零和负整数
(3)利用上面的结论计算:
① 33÷3-7; ②÷.
【解】原式=33-(-7)=310.
原式==-.
22. 阅读下面的材料:
求 的值.
解:设 ,①
则 ,②
,得.所以原式 .
请你仿此计算:
(1) ;
解:设 ,①
则 ,②
,得 ,所以.所以原式 .
(2)( 为大于1的正整数).
解:设 ,①
则 ,②
,得,所以 .所以原式 .
课堂小结
一个性质
由特殊到一般的思考问题的方法
二个幂
同底幂的除法运算法则: am÷an=am–n(a≠0,m、n为整数)
零指数幂
a0 =1 (a≠0)
负指数幂
一个方法
同底数幂除法的运算性质
适用于一切整数指数幂
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
