7.3 数据的描述(第3课时)课件(共46张PPT) 2024-2025学年青岛版七年级数学下册
文档属性
| 名称 | 7.3 数据的描述(第3课时)课件(共46张PPT) 2024-2025学年青岛版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 74.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-10 14:14:29 | ||
图片预览









文档简介
(共46张PPT)
第7章 数据的收集、整理与描述
7.3 数据的描述(3)
学习目标
1. 了解组距、频数、频数直方图等基本概念;
2. 掌握用频数直方图描述数据分布情况的基本步骤,能从频数直方图中获取信息。
问题情境
我们学习了哪些描述数据的方法
它们分别有什么特点
思考与交流
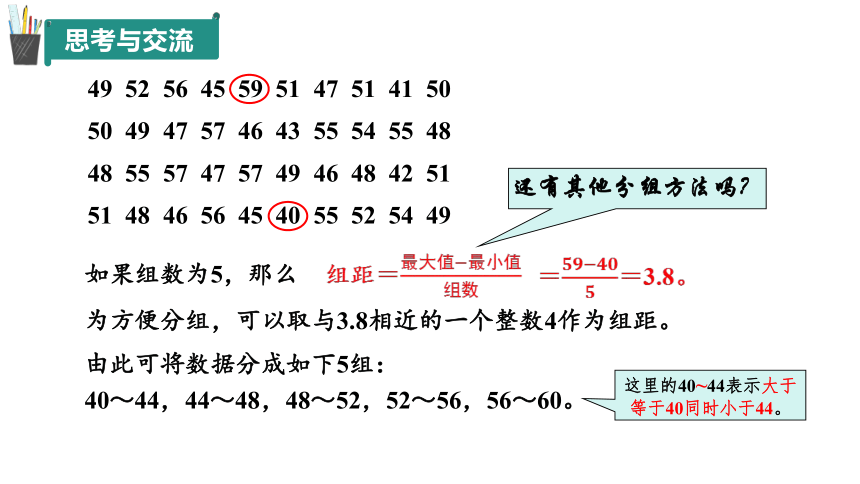
为预估试验田中玉米的长势情况,研究人员对处于生长期的玉米株高进行监测。为降低监测成本,研究人员选取部分玉米,收集了这些玉米株高(单位:cm)的数据:
49 52 56 45 59 51 47 51 41 50
50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51
51 48 46 56 45 40 55 52 54 49
抽取的玉米株高的分布情况如何?
思考与交流
49 52 56 45 59 51 47 51 41 50
50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51
51 48 46 56 45 40 55 52 54 49
为了预估大部分玉米的株高范围,需要先了解抽取的玉米株高范围的分布情况,即哪些株高范围的玉米比较多,哪些株高范围的玉米比较少。
这就需要对上述数据进行适当地分组整理。
思考与交流
(1) 求数据中最大值与最小值的差。
在上面的数据中,玉米株高的最大值是59,最小值是40,
它们的差为
59-40=19。
思考与交流
(2) 确定组数和组距。
将从小到大排列的数据分段,每段中的数据称为一组数据,组的个数称为组数。一般地,样本容量在100以内时,可将数据分成5至12组。每个小组的两个端点之间的距离称为组距。根据解决问题的需要,每组的组距可以相同,也可以不同,通常采用等距分组。
思考与交流
49 52 56 45 59 51 47 51 41 50
50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51
51 48 46 56 45 40 55 52 54 49
如果组数为5,那么
组距=
==3.8。
由此可将数据分成如下5组:
40~44,44~48,48~52,52~56,56~60。
为方便分组,可以取与3.8相近的一个整数4作为组距。
还有其他分组方法吗?
这里的40~44表示大于等于40同时小于44。
思考与交流
数据分组时,组数太少,不能充分显示数据的分布情况;组数太多,容易把性质相近的同类数据分散到各组,也不能较好地显示数据分布的特征和规律。
思考与交流
分组时,根据给定的组数,可以确定组距。也可以先定出组距,再确定组数。
(1)组数的决定方法:设数据总数目为n,一般地,当n≤50时,分为5~8组;当50<n≤100时,分为8~12组。
(2)分点的两种确定方法:
①数据不落在分点上:若数据均为整数,则取某一分组区间的最小值减去0.5作为该分组区间的左分点数据;若数据是保留小数点后一位的数,则取某一分组区间的最小值减去0.05作为该分组区间的左分点数据,以此类推。
②数据落在分点上:需要对每个分组区间的端点值属于哪个组做出规定。 例如分组为:130≤x<140,140≤x<150等。
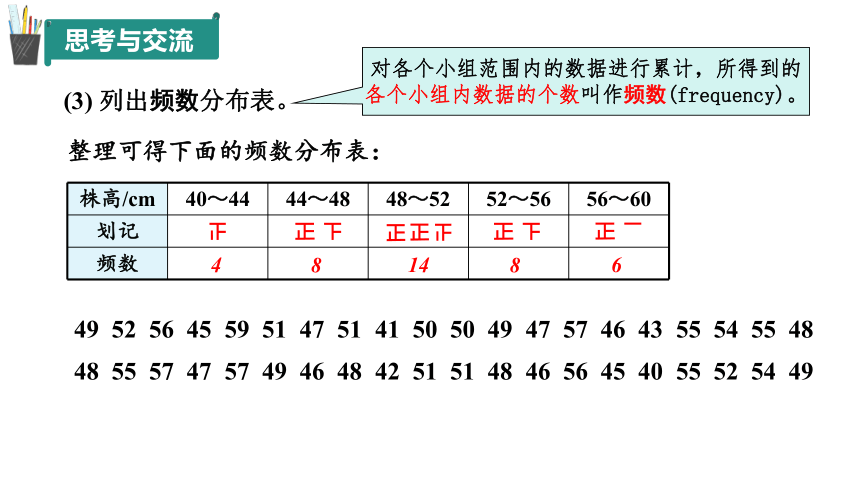
株高/cm 40~44 44~48 48~52 52~56 56~60
划记
频数
思考与交流
(3) 列出频数分布表。
对各个小组范围内的数据进行累计,所得到的各个小组内数据的个数叫作频数(frequency)。
整理可得下面的频数分布表:
49 52 56 45 59 51 47 51 41 50 50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51 51 48 46 56 45 40 55 52 54 49
4
8
14
8
6
思考与交流
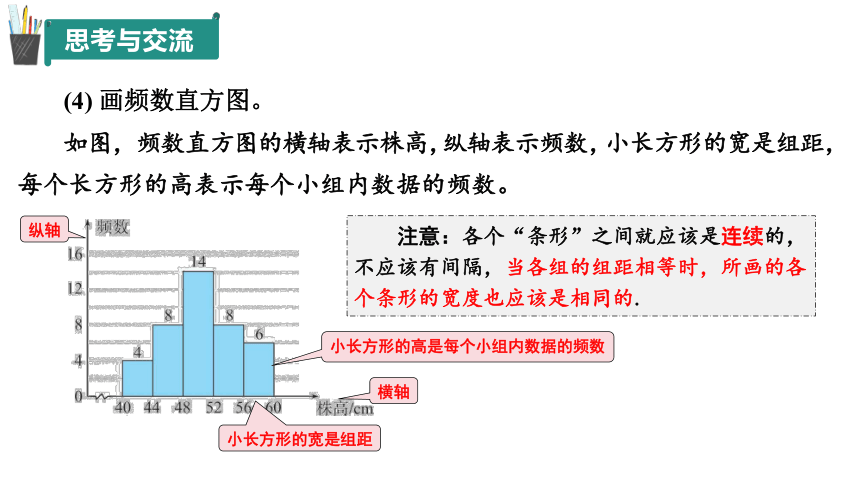
(4) 画频数直方图。
每个长方形的高表示每个小组内数据的频数。
横轴
如图,频数直方图的横轴表示株高,
纵轴表示频数,
纵轴
小长方形的宽是组距
小长方形的宽是组距,
小长方形的高是每个小组内数据的频数
注意:各个“条形”之间就应该是连续的,不应该有间隔,当各组的组距相等时,所画的各个条形的宽度也应该是相同的.
思考与交流
(4) 画频数直方图。
每个长方形的高表示每个小组内数据的频数。
如图,频数直方图的横轴表示株高,
纵轴表示频数,
小长方形的宽是组距,
通过左图可以直接比较各组频数的差异,即组间玉米株数的差异,但从中看不到每组内玉米株高的具体数据。
思考与交流
根据下面的频数直方图,你对抽取的玉米株高的分布情况作出怎样的估计?
从图中看到,株高范围在48~52 cm内的株数最多,有14株,在40~44 cm内的株数最少,有4株。玉米株高大部分集中在44~56 cm之间。
概括与表达
根据频数的分布画出的条形统计图叫作频数直方图(frequency histogram)。
讨论与归纳
用频数直方图描述数据分布情况的基本步骤是什么?
③ 列出频数分布表;
① 求数据中最大值与最小值的差;
② 确定组数和组距;
④ 以横轴表示数据,纵轴表示频数,画出频数直方图。
例题讲解
例1 某中学为了解全校学生课外阅读的情况,随机调查了50名学生一周内平均每天课外阅读的时间(单位:min),调查的数据如下:
30 10 23 26 42 43 48 18 52 31 33 34 26 44 32 21 45 35 22 34
35 27 39 47 26 37 35 28 32 35 48 23 15 34 36 21 32 46 19 38
44 34 44 13 46 34 39 43 59 25
列出频数分布表,画出频数直方图。
例题讲解
解:(1) 求数据中最大值与最小值的差。
59-10=49。
数据的最大值是59,最小值是10,它们的差是
(2) 确定组数和组距。
如果取组数为5,那么组距为
=9.8。
所以将数据分成如下5组:
10~20,20~30,30~40,40~50,50~60。
取与9.8相近的一个整数10作为组距。
例题讲解
组别 1 2 3 4 5
时间/min 10~20 20~30 30~40 40~50 50~60
频数 5 11 20 12 2
(3) 列出频数分布表。
例题讲解
(4) 画频数直方图。
讨论与交流
条形统计图与频数直方图有什么区别和联系?
(1)联系:用途都是可以直观地表示出具体数量。频数直方图是特殊的条形统计图。
(3)绘制的形式不同:条形统计图各条形分开;频数直方图的条形连在一起。
(2)区别:条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况。
新知巩固
为了解七年级学生的体能状况,某学校体育老师随机调查了32名学生1 min内蹲起的次数,数据如下:
48 22 54 55 37 35 26 38 51 47 38 32 23 48 32 52
23 46 35 43 37 30 25 43 42 34 21 30 34 38 37 48
列出样本的频数分布表,画出频数直方图。
解:最大值与最小值的差为55-21=34。取组距为5。则34÷5=6.8。
所以分成7组。列频数分布表如下:
新知巩固
组别 1 2 3 4 5 6 7
次数 21~25 25~30 30~35 35~40 40~45 45~50 50~55
频数 5 2 5 8 3 5 4
次数
频数
21
25
30
35
40
45
50
55
画频数直方图:
拓展与延伸
例2 镇政府想了解李家庄130户家庭的经济情况,从中随机抽取了部分家庭进行调查,获得了他们的年收入x(单位:万元),并对数据(年收入)进行整理、描述和分析,下面给出了部分信息。
被抽取的部分家庭年收入的频数分布直方图和扇形统计图如图所示
(数据分组:A:0.9≤x<1.3,B:1.3≤x<1.7,C:1.7≤x<2.1,D:2.1≤x<2.5,E:2.5≤x<2.9,F:2.9≤x<3.3).
拓展与延伸
根据以上信息,回答下列问题:
(1)将两个统计图补充完整;
解:(1)抽查的家庭总数为3÷15%=20(户),
家庭年收入在2.1≤x<2.5这一组的户数为
20-(3+6+3+2+1)=5(户),
家庭年收入在2.1≤x<2.5这一组所占
的百分比为×100%=25%,
两统计图补充如图:
5
25
拓展与延伸
解:(2)130×=52(户)。
即估计李家庄有52户家庭年收入不低于1.7万元且不足2.5万元。
根据以上信息,回答下列问题:
(2)估计李家庄有多少户家庭年收入不低于1.7万元且不足2.5万元。
1.绘制频数直方图的基本步骤。
2.从频数直方图中获取信息。
课堂检测
基础过关
1.在频数分布表中,各小组的频数之和 ( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
B
课堂检测
基础过关
2.为了解公园用地面积x (单位:公顷)的基本情况,某地随机调查了本地50个公园的用地面积,按照0<x≤4,4<x≤8,8<x≤12,12<x≤16,16<x≤20的分组绘制了如图所示的频数分布直方图,下列说法正确的是 ( )
B
A.a的值为20
B.用地面积在8<x≤12这一组的公园个数最多
C.用地面积在4<x≤8这一组的公园个数最少
D.这50个公园中有一半以上的公园用地面积超过12公顷
课堂检测
基础过关
3.统计得到的一组数据有80个,其中最大值为139,最小值为48,取组距为10,则可分成________。
10组
4.某班40名学生体重的频数分布直方图(不完整)如图所示,组距为_____kg。
5
kg
课堂检测
基础过关
5.某地区随机抽调了一部分市民进行了一次法律知识测试,测试成绩(得分取整数)进行整理后分成五组,并绘制成频数直方图:
(1)这次活动共抽取了多少人测试?
(2)测试成绩的整体分布情况怎样?
解:(1)根据题意得:3+12+18+9+6=48(人),
答:这次活动共抽取了48人测试;
(2)根据统计图可知:测试成绩为70至80分的人数
最多,不及格和90分以上的人相对较少。
课堂检测
基础过关
6.为了调查居民的生活水平,有关部门对某个地区5个街道的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.6 3.5 2.3 6.5 2.2 1.9 6.8 4.8 5.0 4.7 2.3
1.5 3.1 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8 3.0
5.1 7.0 3.1 2.9 4.4 5.8 3.8 3.7 3.3 5.2 4.1
4.2 4.8 3.0 4.0 4.6 6.0 2.4 3.3 6.1 5.0 4.9
3.0 3.1 7.2 1.8 5.0 1.9
将数据适当分组,并绘制相应的频数直方图。
课堂检测
基础过关
解:第一步,计算最大值与最小值的差:
在所给的数据中,最大值是7.2,最小值是1.5,它们的差是7.2-1.5=5.7。
第二步,决定组距与组数:
由于最大值与最小值的差是5.7,如果取组距为1,那么由于,可分成6组,
组数合适,于是取组距为1,组数为6。
课堂检测
基础过关
分组 频数
10
10
11
10
5
4
合计 50
第三步,列频数分布表:
课堂检测
基础过关
第四步,画频数直方图:
课堂检测
能力提升
1.对频数分布直方图的下列认识,不正确的是( )
A.每小组条形图的横宽等于这组的组距
B.每小组条形图的纵高等于这组的频数
C.每小组条形图的面积等于这组的频数
D.所有小组条形图的个数等于数据分组整理的组数
C
课堂检测
能力提升
2.“俭以养德”是中华民族的优秀传统,时代中学为了对全校学生零花钱的使用进行正确引导,随机抽取50名学生,对他们一周的零花钱数额进行了统计,并根据调查结果绘制了如右不完整的频数分布表和扇形统计图.
关于这次调查,下列说法正确的是( )
A.总体为50名学生一周的零花钱数额
B.五组对应扇形的圆心角度数为36°
C.在这次调查中,四组的频数为6
D.若该校共有学生1500人,则估计该校
零花钱数额不超过20元的人数为1200
B
组别 零花钱数额x/元 频数
一 x≤10
二 10<x≤15 12
三 15<x≤20 15
四 20<x≤25 a
五 x>25 5
课堂检测
3. 某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8。则下列说法:
① 该班有50名同学参赛;
② 第五组的百分比为16%;
③ 成绩在70~80分的人数最多;
④ 80分以上的学生有14名,
其中正确的有_____个。
3
能力提升
课堂检测
能力提升
4. 如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有______人。
20
课堂检测
能力提升
5.从蔬菜大棚中收集到50株西红柿秧上小西红柿的个数:
28 62 54 29 32 47 68 27 55 43
36 79 46 54 25 82 16 39 32 64
61 59 67 56 45 74 49 36 39 52
85 65 48 58 59 64 91 67 54 57
68 54 71 26 59 47 58 52 52 70
请按组距为10将数据分组,列出频数分布表。画出频数分布直方图,分析数据分布的情况。
课堂检测
能力提升
解:频数分布表:
个数 划记 频数
一 1
正丅 7
正 5
正正 13
正正丅 12
正 8
丅 2
丅 2
合计 50
课堂检测
能力提升
频数分布直方图:
课堂检测
能力提升
从统计图表中可以看出,一株西红柿秧上结出西红柿的个数在45~65范围的最多,约占总株数的一半;其次,个数在25~35和65~75的共15株,占总株数的30%;个数在25以下的只有1株,占总株数的2%;个数在75以上的有4株,占总株数的8%。
课堂检测
能力提升
6.为落实视力保护工作,某校组织七年级学生开展了视力保健活动。活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据:
4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动前被测查学生视力数据:
课堂检测
能力提升
活动后被测查学生视力频数分布表
分组 频数
4.0≤x<4.2 1
4.2≤x<4.4 2
4.4≤x<4.6 b
4.6≤x<4.8 7
4.8≤x<5.0 12
5.0≤x<5.2 4
根据以上信息回答下列问题:
课堂检测
能力提升
(1)填空:a=________,b=________;
5
4
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少;
解:七年级600名学生活动后视力达标的人数为600×=320。
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.
解:答案不唯一,能说明问题即可。比如:
视力在4.8≤x<5.2的被测查学生活动前有11人,活动后有16人,人数明显增加,
说明视力保健活动的效果比较好。
第7章 数据的收集、整理与描述
7.3 数据的描述(3)
学习目标
1. 了解组距、频数、频数直方图等基本概念;
2. 掌握用频数直方图描述数据分布情况的基本步骤,能从频数直方图中获取信息。
问题情境
我们学习了哪些描述数据的方法
它们分别有什么特点
思考与交流
为预估试验田中玉米的长势情况,研究人员对处于生长期的玉米株高进行监测。为降低监测成本,研究人员选取部分玉米,收集了这些玉米株高(单位:cm)的数据:
49 52 56 45 59 51 47 51 41 50
50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51
51 48 46 56 45 40 55 52 54 49
抽取的玉米株高的分布情况如何?
思考与交流
49 52 56 45 59 51 47 51 41 50
50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51
51 48 46 56 45 40 55 52 54 49
为了预估大部分玉米的株高范围,需要先了解抽取的玉米株高范围的分布情况,即哪些株高范围的玉米比较多,哪些株高范围的玉米比较少。
这就需要对上述数据进行适当地分组整理。
思考与交流
(1) 求数据中最大值与最小值的差。
在上面的数据中,玉米株高的最大值是59,最小值是40,
它们的差为
59-40=19。
思考与交流
(2) 确定组数和组距。
将从小到大排列的数据分段,每段中的数据称为一组数据,组的个数称为组数。一般地,样本容量在100以内时,可将数据分成5至12组。每个小组的两个端点之间的距离称为组距。根据解决问题的需要,每组的组距可以相同,也可以不同,通常采用等距分组。
思考与交流
49 52 56 45 59 51 47 51 41 50
50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51
51 48 46 56 45 40 55 52 54 49
如果组数为5,那么
组距=
==3.8。
由此可将数据分成如下5组:
40~44,44~48,48~52,52~56,56~60。
为方便分组,可以取与3.8相近的一个整数4作为组距。
还有其他分组方法吗?
这里的40~44表示大于等于40同时小于44。
思考与交流
数据分组时,组数太少,不能充分显示数据的分布情况;组数太多,容易把性质相近的同类数据分散到各组,也不能较好地显示数据分布的特征和规律。
思考与交流
分组时,根据给定的组数,可以确定组距。也可以先定出组距,再确定组数。
(1)组数的决定方法:设数据总数目为n,一般地,当n≤50时,分为5~8组;当50<n≤100时,分为8~12组。
(2)分点的两种确定方法:
①数据不落在分点上:若数据均为整数,则取某一分组区间的最小值减去0.5作为该分组区间的左分点数据;若数据是保留小数点后一位的数,则取某一分组区间的最小值减去0.05作为该分组区间的左分点数据,以此类推。
②数据落在分点上:需要对每个分组区间的端点值属于哪个组做出规定。 例如分组为:130≤x<140,140≤x<150等。
株高/cm 40~44 44~48 48~52 52~56 56~60
划记
频数
思考与交流
(3) 列出频数分布表。
对各个小组范围内的数据进行累计,所得到的各个小组内数据的个数叫作频数(frequency)。
整理可得下面的频数分布表:
49 52 56 45 59 51 47 51 41 50 50 49 47 57 46 43 55 54 55 48
48 55 57 47 57 49 46 48 42 51 51 48 46 56 45 40 55 52 54 49
4
8
14
8
6
思考与交流
(4) 画频数直方图。
每个长方形的高表示每个小组内数据的频数。
横轴
如图,频数直方图的横轴表示株高,
纵轴表示频数,
纵轴
小长方形的宽是组距
小长方形的宽是组距,
小长方形的高是每个小组内数据的频数
注意:各个“条形”之间就应该是连续的,不应该有间隔,当各组的组距相等时,所画的各个条形的宽度也应该是相同的.
思考与交流
(4) 画频数直方图。
每个长方形的高表示每个小组内数据的频数。
如图,频数直方图的横轴表示株高,
纵轴表示频数,
小长方形的宽是组距,
通过左图可以直接比较各组频数的差异,即组间玉米株数的差异,但从中看不到每组内玉米株高的具体数据。
思考与交流
根据下面的频数直方图,你对抽取的玉米株高的分布情况作出怎样的估计?
从图中看到,株高范围在48~52 cm内的株数最多,有14株,在40~44 cm内的株数最少,有4株。玉米株高大部分集中在44~56 cm之间。
概括与表达
根据频数的分布画出的条形统计图叫作频数直方图(frequency histogram)。
讨论与归纳
用频数直方图描述数据分布情况的基本步骤是什么?
③ 列出频数分布表;
① 求数据中最大值与最小值的差;
② 确定组数和组距;
④ 以横轴表示数据,纵轴表示频数,画出频数直方图。
例题讲解
例1 某中学为了解全校学生课外阅读的情况,随机调查了50名学生一周内平均每天课外阅读的时间(单位:min),调查的数据如下:
30 10 23 26 42 43 48 18 52 31 33 34 26 44 32 21 45 35 22 34
35 27 39 47 26 37 35 28 32 35 48 23 15 34 36 21 32 46 19 38
44 34 44 13 46 34 39 43 59 25
列出频数分布表,画出频数直方图。
例题讲解
解:(1) 求数据中最大值与最小值的差。
59-10=49。
数据的最大值是59,最小值是10,它们的差是
(2) 确定组数和组距。
如果取组数为5,那么组距为
=9.8。
所以将数据分成如下5组:
10~20,20~30,30~40,40~50,50~60。
取与9.8相近的一个整数10作为组距。
例题讲解
组别 1 2 3 4 5
时间/min 10~20 20~30 30~40 40~50 50~60
频数 5 11 20 12 2
(3) 列出频数分布表。
例题讲解
(4) 画频数直方图。
讨论与交流
条形统计图与频数直方图有什么区别和联系?
(1)联系:用途都是可以直观地表示出具体数量。频数直方图是特殊的条形统计图。
(3)绘制的形式不同:条形统计图各条形分开;频数直方图的条形连在一起。
(2)区别:条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况。
新知巩固
为了解七年级学生的体能状况,某学校体育老师随机调查了32名学生1 min内蹲起的次数,数据如下:
48 22 54 55 37 35 26 38 51 47 38 32 23 48 32 52
23 46 35 43 37 30 25 43 42 34 21 30 34 38 37 48
列出样本的频数分布表,画出频数直方图。
解:最大值与最小值的差为55-21=34。取组距为5。则34÷5=6.8。
所以分成7组。列频数分布表如下:
新知巩固
组别 1 2 3 4 5 6 7
次数 21~25 25~30 30~35 35~40 40~45 45~50 50~55
频数 5 2 5 8 3 5 4
次数
频数
21
25
30
35
40
45
50
55
画频数直方图:
拓展与延伸
例2 镇政府想了解李家庄130户家庭的经济情况,从中随机抽取了部分家庭进行调查,获得了他们的年收入x(单位:万元),并对数据(年收入)进行整理、描述和分析,下面给出了部分信息。
被抽取的部分家庭年收入的频数分布直方图和扇形统计图如图所示
(数据分组:A:0.9≤x<1.3,B:1.3≤x<1.7,C:1.7≤x<2.1,D:2.1≤x<2.5,E:2.5≤x<2.9,F:2.9≤x<3.3).
拓展与延伸
根据以上信息,回答下列问题:
(1)将两个统计图补充完整;
解:(1)抽查的家庭总数为3÷15%=20(户),
家庭年收入在2.1≤x<2.5这一组的户数为
20-(3+6+3+2+1)=5(户),
家庭年收入在2.1≤x<2.5这一组所占
的百分比为×100%=25%,
两统计图补充如图:
5
25
拓展与延伸
解:(2)130×=52(户)。
即估计李家庄有52户家庭年收入不低于1.7万元且不足2.5万元。
根据以上信息,回答下列问题:
(2)估计李家庄有多少户家庭年收入不低于1.7万元且不足2.5万元。
1.绘制频数直方图的基本步骤。
2.从频数直方图中获取信息。
课堂检测
基础过关
1.在频数分布表中,各小组的频数之和 ( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
B
课堂检测
基础过关
2.为了解公园用地面积x (单位:公顷)的基本情况,某地随机调查了本地50个公园的用地面积,按照0<x≤4,4<x≤8,8<x≤12,12<x≤16,16<x≤20的分组绘制了如图所示的频数分布直方图,下列说法正确的是 ( )
B
A.a的值为20
B.用地面积在8<x≤12这一组的公园个数最多
C.用地面积在4<x≤8这一组的公园个数最少
D.这50个公园中有一半以上的公园用地面积超过12公顷
课堂检测
基础过关
3.统计得到的一组数据有80个,其中最大值为139,最小值为48,取组距为10,则可分成________。
10组
4.某班40名学生体重的频数分布直方图(不完整)如图所示,组距为_____kg。
5
kg
课堂检测
基础过关
5.某地区随机抽调了一部分市民进行了一次法律知识测试,测试成绩(得分取整数)进行整理后分成五组,并绘制成频数直方图:
(1)这次活动共抽取了多少人测试?
(2)测试成绩的整体分布情况怎样?
解:(1)根据题意得:3+12+18+9+6=48(人),
答:这次活动共抽取了48人测试;
(2)根据统计图可知:测试成绩为70至80分的人数
最多,不及格和90分以上的人相对较少。
课堂检测
基础过关
6.为了调查居民的生活水平,有关部门对某个地区5个街道的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.6 3.5 2.3 6.5 2.2 1.9 6.8 4.8 5.0 4.7 2.3
1.5 3.1 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8 3.0
5.1 7.0 3.1 2.9 4.4 5.8 3.8 3.7 3.3 5.2 4.1
4.2 4.8 3.0 4.0 4.6 6.0 2.4 3.3 6.1 5.0 4.9
3.0 3.1 7.2 1.8 5.0 1.9
将数据适当分组,并绘制相应的频数直方图。
课堂检测
基础过关
解:第一步,计算最大值与最小值的差:
在所给的数据中,最大值是7.2,最小值是1.5,它们的差是7.2-1.5=5.7。
第二步,决定组距与组数:
由于最大值与最小值的差是5.7,如果取组距为1,那么由于,可分成6组,
组数合适,于是取组距为1,组数为6。
课堂检测
基础过关
分组 频数
10
10
11
10
5
4
合计 50
第三步,列频数分布表:
课堂检测
基础过关
第四步,画频数直方图:
课堂检测
能力提升
1.对频数分布直方图的下列认识,不正确的是( )
A.每小组条形图的横宽等于这组的组距
B.每小组条形图的纵高等于这组的频数
C.每小组条形图的面积等于这组的频数
D.所有小组条形图的个数等于数据分组整理的组数
C
课堂检测
能力提升
2.“俭以养德”是中华民族的优秀传统,时代中学为了对全校学生零花钱的使用进行正确引导,随机抽取50名学生,对他们一周的零花钱数额进行了统计,并根据调查结果绘制了如右不完整的频数分布表和扇形统计图.
关于这次调查,下列说法正确的是( )
A.总体为50名学生一周的零花钱数额
B.五组对应扇形的圆心角度数为36°
C.在这次调查中,四组的频数为6
D.若该校共有学生1500人,则估计该校
零花钱数额不超过20元的人数为1200
B
组别 零花钱数额x/元 频数
一 x≤10
二 10<x≤15 12
三 15<x≤20 15
四 20<x≤25 a
五 x>25 5
课堂检测
3. 某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8。则下列说法:
① 该班有50名同学参赛;
② 第五组的百分比为16%;
③ 成绩在70~80分的人数最多;
④ 80分以上的学生有14名,
其中正确的有_____个。
3
能力提升
课堂检测
能力提升
4. 如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有______人。
20
课堂检测
能力提升
5.从蔬菜大棚中收集到50株西红柿秧上小西红柿的个数:
28 62 54 29 32 47 68 27 55 43
36 79 46 54 25 82 16 39 32 64
61 59 67 56 45 74 49 36 39 52
85 65 48 58 59 64 91 67 54 57
68 54 71 26 59 47 58 52 52 70
请按组距为10将数据分组,列出频数分布表。画出频数分布直方图,分析数据分布的情况。
课堂检测
能力提升
解:频数分布表:
个数 划记 频数
一 1
正丅 7
正 5
正正 13
正正丅 12
正 8
丅 2
丅 2
合计 50
课堂检测
能力提升
频数分布直方图:
课堂检测
能力提升
从统计图表中可以看出,一株西红柿秧上结出西红柿的个数在45~65范围的最多,约占总株数的一半;其次,个数在25~35和65~75的共15株,占总株数的30%;个数在25以下的只有1株,占总株数的2%;个数在75以上的有4株,占总株数的8%。
课堂检测
能力提升
6.为落实视力保护工作,某校组织七年级学生开展了视力保健活动。活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据:
4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动前被测查学生视力数据:
课堂检测
能力提升
活动后被测查学生视力频数分布表
分组 频数
4.0≤x<4.2 1
4.2≤x<4.4 2
4.4≤x<4.6 b
4.6≤x<4.8 7
4.8≤x<5.0 12
5.0≤x<5.2 4
根据以上信息回答下列问题:
课堂检测
能力提升
(1)填空:a=________,b=________;
5
4
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少;
解:七年级600名学生活动后视力达标的人数为600×=320。
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.
解:答案不唯一,能说明问题即可。比如:
视力在4.8≤x<5.2的被测查学生活动前有11人,活动后有16人,人数明显增加,
说明视力保健活动的效果比较好。
同课章节目录
