沪教版八年级数学下册 22.3.1 特殊的平行四边形--矩形(含解析)
文档属性
| 名称 | 沪教版八年级数学下册 22.3.1 特殊的平行四边形--矩形(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-11 00:00:00 | ||
图片预览



文档简介
22.3.1 特殊的平行四边形--矩形
一、单选题
1.下列性质中,矩形具有而一般平行四边形不具有的是( ).
A.对边相等 B.对角相等 C.对角线相等 D.对边平行
2.如图,矩形ABCD的对角线,则BD的长为( )
A.3cm B.4cm C.5cm D.6cm
3.如图,矩形的对角线、相交于点,,,则矩形的对角线长为( )
A. B. C. D.
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
5.在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是( )
A.AB=CD,AD=BC,AC=BD B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,AC⊥BD D.∠A=∠B=90°,AC=BD
6.已知四边形ABCD的对角线相交于点O,且OA=OB=OC=OD,那么这个四边形是( )
A.是中心对称图形,但不是轴对称图形 B.是轴对称图形,但不是中心对称图形
C.既是中心对称图形,又是轴对称图形 D.既不是中心对称图形,又不是轴对称图形
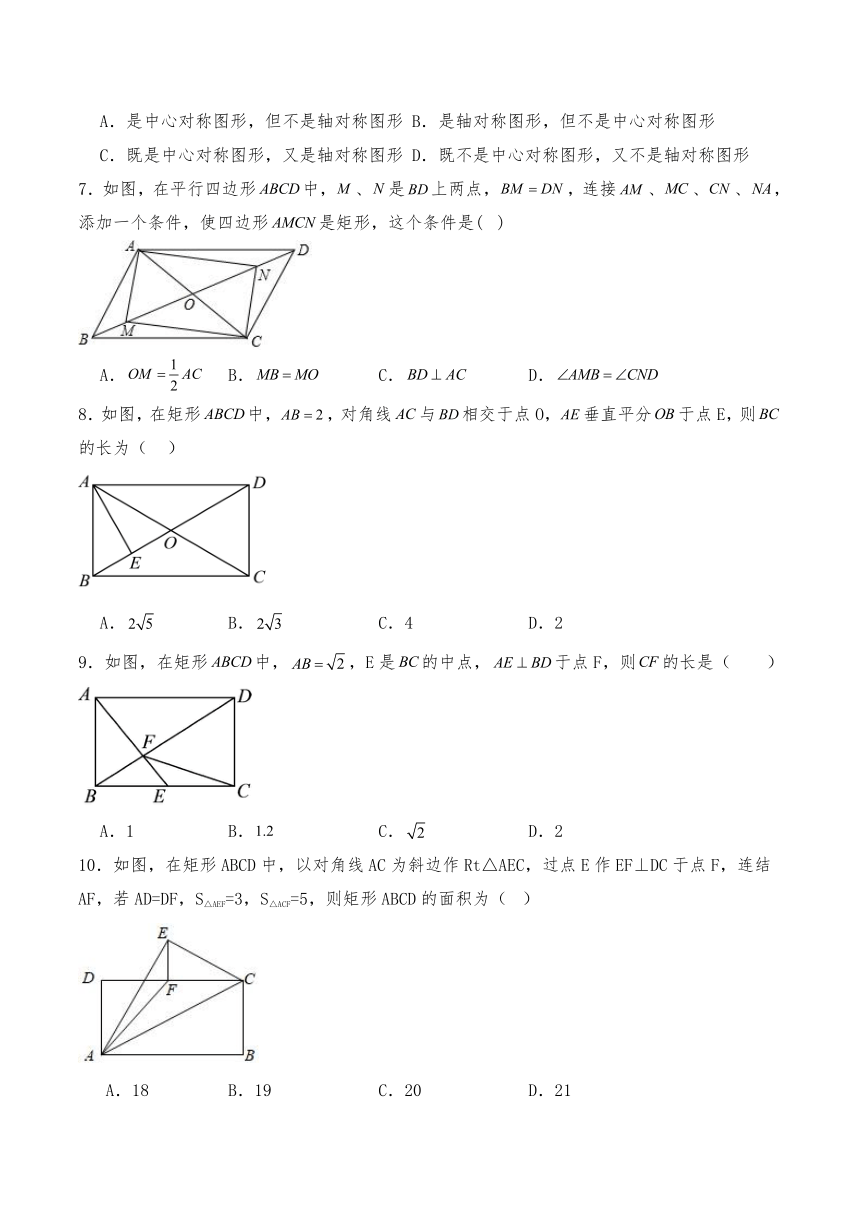
7.如图,在平行四边形中,、是上两点,,连接、、、,添加一个条件,使四边形是矩形,这个条件是( )
A. B. C. D.
8.如图,在矩形中,,对角线与相交于点O,垂直平分于点E,则的长为( )
A. B. C.4 D.2
9.如图,在矩形中,,E是的中点,于点F,则的长是( )
A.1 B. C. D.2
10.如图,在矩形ABCD中,以对角线AC为斜边作Rt△AEC,过点E作EF⊥DC于点F,连结AF,若AD=DF,S△AEF=3,S△ACF=5,则矩形ABCD的面积为( )
A.18 B.19 C.20 D.21
二、填空题
11.矩形的两条对角线的夹角为,较短的边长为,则对角线长为 .
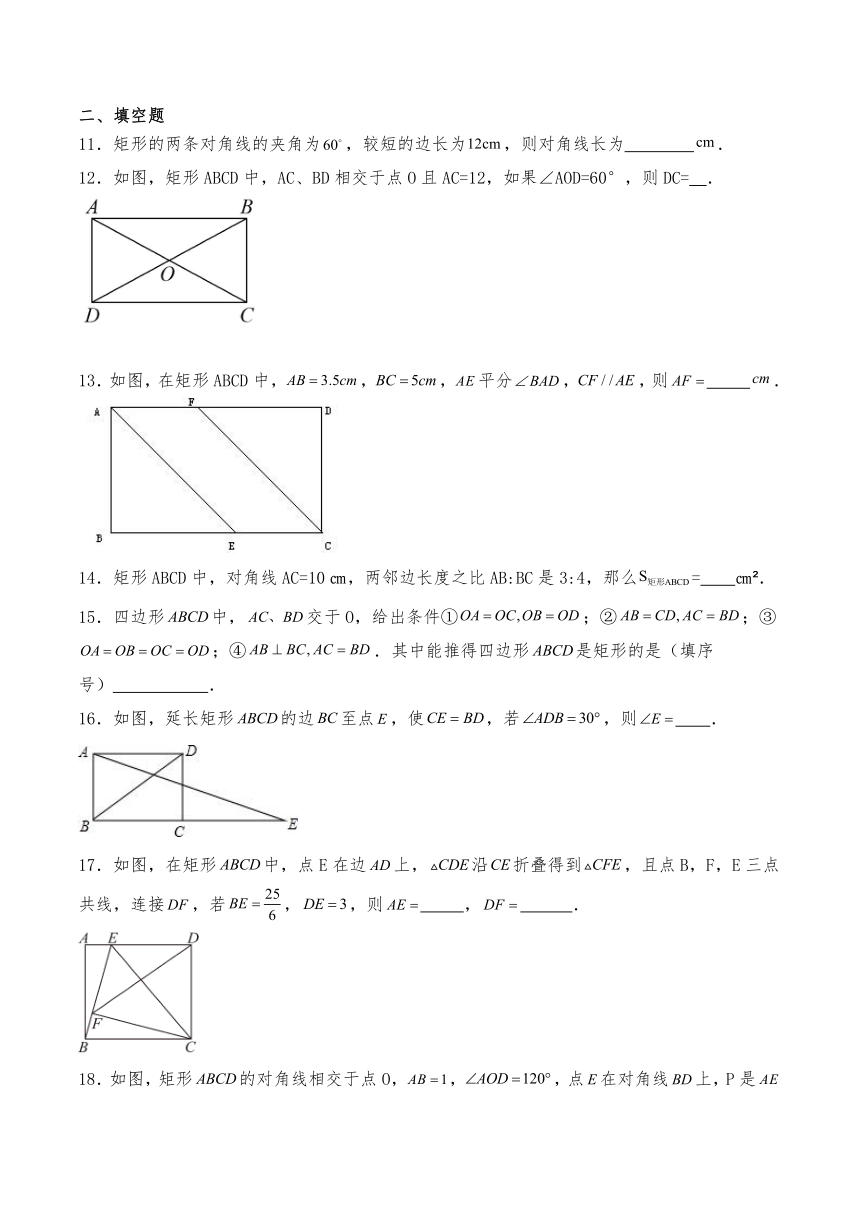
12.如图,矩形ABCD中,AC、BD相交于点O且AC=12,如果∠AOD=60°,则DC= .
13.如图,在矩形ABCD中,,,平分,,则 .
14.矩形ABCD中,对角线AC=10㎝,两邻边长度之比AB:BC是3:4,那么= ㎝ .
15.四边形中,交于O,给出条件①;②;③;④.其中能推得四边形是矩形的是(填序号) .
16.如图,延长矩形的边至点,使,若,则 .
17.如图,在矩形中,点E在边上,沿折叠得到,且点B,F,E三点共线,连接,若,,则 , .
18.如图,矩形的对角线相交于点O,,,点在对角线上,P是的中点,的最小值是 .
三、解答题
19.已知:如图,四边形是矩形,,对角线与相交于点O.
求证:
(1);
(2).
20.如图 ABCD,四个内角的平分线相交于E、F、G、H四个点;
求证:四边形EFGH是矩形.
21.如图,在中,为边上的中线,延长至E,使,连接,.
(1)试判断四边形的形状;
(2)当满足什么条件时,四边形是矩形?
22.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠DAB,CF=3,BF=4,求DF长.
23.如图,矩形ABCD的对角线相交于点,且.
(1)求证:四边形是矩形;
(2)点在上,连接,若,求的面积.
24.如图,在矩形中,,,动点P从点A开始沿边以的速度运动,动点Q从点C开始沿边以的速度运动.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动.设动点的运动时间为.
(1)用含t的代数式表示 ;
(2)若四边形为矩形,求t的值;
(3)是否存在t值,使线段的长为?若存在,直接写出t的值;若不存在,说明理由.
25.如图,在矩形中,是边上一点,连接,过点作交于点,连接.
(1)如图1,若,求证:.
(2)如图2,若恰好是边的中点,求证:.
(3)在(2)的条件下,当,时,求的值.
26.如图,在矩形中,,,点E是上一点.将沿折叠后,得到.点F在矩形内部,延长交于点G.
(1)如图①,当点E是中点时,求的长;
(2)如图②,在(1)的条件下,当矩形变化为平行四边形时,求证:;
(3)如图③,在矩形中,当点F落在矩形对角线上时,的长是
27.如图1,点是矩形边上一点(不与点,重合),直线与的延长线交于点.将沿直线折叠得到,点在矩形的内部,延长交直线于点.
(1)证明:;
(2)如图2,连接,若,,求周长的最小值;
(3)如图3,连接交于点,点是的中点,当时,请判断与的数量关系,并说明理由.
答案
一、单选题
1.C
【分析】由矩形的性质和平行四边形的性质即可得出结论.
【解析】解:∵矩形的对边相等,对角相等,对角线互相平分且相等;
平行四边形的对边相等,对角相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选C.
2.D
【分析】根据矩形的性质可知AC=BD且AO=CO,根据AO=3,求出AC,进一步求BD即可.
【解析】解:∵四边形ABCD是矩形,
∴AC=BD,AO=OC,
∵AO=3cm,
∴AC=2AO=6cm,
∴BD=6cm.
故选:D.
3.C
【分析】根据矩形性质得出,,,,推出,求出等边三角形,求出,即可得出答案.
【解析】,
,
四边形是矩形,
,,,,
,
,
是等边三角形,
,
,
,.
故选C.
4.B
【分析】根据矩形的性质可得OA=OD,从而得到∠ADO=55°,再由,即可求解.
【解析】解:在矩形ABCD中,OA=OD,
∴∠ADO=∠DAO,
∵∠AOB=∠ADO+∠DAO,,
∴∠ADO=55°,
∵,即∠AED=90°,
∴∠DAE=35°.
故选:B
5.C
【解析】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,
∴A正确;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
又,
∴四边形ABCD是矩形,
∴B正确;
∵∠A=∠C,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴C不正确;
如图所示:
在和中,
∴BC=AD,
∴四边形ABCD是平行四边形,
又 ∴四边形ABCD是矩形,
∴D正确;
故选:C
6.C
【分析】先根据已知条件OA=OB=OC=OD,可知四边形ABCD的对角线相等且互相平分,得出四边形ABCD是矩形,然后根据矩形的对称性,得出结果.
【解析】解:如图所示:
∵四边形ABCD的对角线相交于点O且OA=OB=OC=OD,
∴OA=OC,OB=OD;AC=BD,
∴四边形ABCD是矩形,
∴四边形ABCD既是轴对称图形,又是中心对称图形.
故选:C.
7.A
【分析】由平行四边形的性质可知:,,再证明即可证明四边形是平行四边形.
【解析】∵四边形是平行四边形,
∴,,
∵对角线上的两点、满足,
∴,即,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形.
故选:A.
8.B
【分析】此题考查了矩形的性质、线段垂直平分线的性质以及勾股定理,由矩形的性质和线段垂直平分线的性质证出,得出,由勾股定理求出即可.
【解析】解:∵四边形是矩形,
∴,,,
∴,
∵垂直平分,
∴,
∵,
∴,
∴,
故选:B.
9.C
【分析】延长交于点M,可证得,从而得到,进而得到,再由直角三角形的性质,即可求解.
【解析】解:如图,延长交于点M,
∵E是的中点,
∴,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∴,
∵,即,
∴,
故选:C
10.B
【分析】过点E作EG垂直AD延长线于点G,然后通过已知三角形的面积得到EF和FC的比值,从而设EF和FC的长度分别为3b和5b,AD和DF的长度为a,然后利用Rt△GEA,Rt△EFC,Rt△CEA,Rt△DAC中的勾股定理得到a与b的关系,再利用△AEF的面积求出a和b的值,最后求矩形ABCD的面积.
【解析】解:过点E作EG⊥AD交AD的延长线与G
∵EF⊥DC
∴ ,
∵DF=AD
∴EF:CF=3∶5
设EF=3b,CF=5b,AD=DF=a
∵∠G=90°,∠EFD=90°,∠GDF=90°
∴四边形EFDG是矩形
∴GE=DF=a,GD=EF=3b
在Rt△GEA中,
在Rt△EFC中,
在Rt△CEA中,
∴
=
=
在Rt△DAC中,
∴=
∴
∵b>0
∴
∴
∴
∴a=
∴
故选:B.
二、填空题
11.24
【分析】根据矩形对角线相等且互相平分性质和题中条件得△AOB为等边三角形,即可得到矩形对角线一半长,进而求解即可.
【解析】解:如图所示,
∵四边形ABCD是矩形,AC,BD是对角线,
∴AC=BD,
OA=OB=OD=OC=BD=AC,
在△AOB中,OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
OA=OB=AB=12cm,
则BD=2OB=2×12=24(cm),
故答案为24.
12.
【分析】根据矩形的对角线互相平分且相等可得OA=OD,然后判断出△AOD是等边三角形,再根据勾股定理解答即可.
【解析】解:∵四边形ABCD是矩形,
∴OA=OD=AC=×12=6,∠ADC=90°,
∵∠AOD=60°,
∴△AOD是等边三角形,
∴AD=OA=6,
∴.
故答案为:.
13.1.5.
【分析】根据题意画出图形,由题意得出△CDF是等腰直角三角形即可得出DF的长,从而得出AF.
【解析】由题意画出图形如下:
∵ABCD是矩形,
∴AD=BC=5cm,CD=AB=3.5cm,
∵AE平分∠BAD,CF∥AE,
∴△ABE和△CDF是等腰直角三角形,
∴DF=CD=3.5cm,
∴AF=AD-AF=1.5cm.
故答案为:1.5.
14.48
【分析】根据题意,画出图形,设AB=3xcm,BC=4xcm,根据勾股定理列出方程即可求出x,从而求出AB和BC,最后根据矩形的面积公式计算即可.
【解析】解:如下图所示,设AB=3xcm,BC=4xcm,
根据勾股定理AB2+BC2=AC2
即,
解得:x=2或-2(不符合实际,舍去)
∴AB=6cm,BC=8cm
∴=cm2
故答案为:48.
15.③
【分析】由矩形的判定、平行四边形的判定与性质分别对各个选项进行判断即可.
【解析】①∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,不符合题意;
②,
不能判定四边形ABCD是矩形,不符合题意;
③∵OA=OB=OC=OD,
∴四边形ABCD是平行四边形,
∴AC=BD,
∴平行四边形ABCD是矩形,符合题意;
④,
不能推出四边形ABCD是矩形,不符合题意;
故答案为:③.
16.15°
【分析】连接AC,由矩形性质可得∠E=∠DAE、BD=AC=CE,知∠E=∠CAE,而∠ADB=∠CAD=30°,可得∠E度数.
【解析】解:连接AC,
∵四边形ABCD是矩形,
∴AC=BD,AD=AD,AB=CD,
∴△ABD≌△DCA,
∴∠ADB=∠CAD=30°,
∵AD∥BE,
∴∠E=∠DAE,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠CAD=∠CAE+∠DAE,
∴∠E+∠E=30°,即∠E=15°,
故答案为:15°.
17.
【分析】本题考查勾股定理,矩形的性质,折叠的性质,掌握矩形的性质是解题的关键.设交于H,,,根据勾股定理得到,,解得,,然后根据三角形的面积求出解题即可.
【解析】解:设交于H,如图:
设,,
∵沿折叠得到,
∴,,
∵,
∴,
在中,,
∴①,
在中,,
∴②,
①②联立解得,或(舍去),
∴,,
∴;
,
∵沿折叠得到,
∴,,
∴,
∴,
∴;
故答案为:,.
18.
【分析】此题重点考查矩形的性质、轴对称的性质、等边三角形的判定与性质、三角形的中位线定理、直角三角形中30°角所对的直角边等于斜边的一半、勾股定理、两点之间线段最短等知识,正确地作出所需要的辅助线是解题的关键.取的中点F,再作B关于的对称点H,与交于点G,连接,求出,再利用三角形的三边关系可得答案.
【解析】解:取的中点F,作直线,
∵点P是的中点,
∴,
∴,
作点B关于直线的对称点H,连接交直线于点G,连接,
∵垂直平分,
∴,,
∵四边形是矩形,,
∴,,,,
∴,
∵,
∴,
∴是等边三角形,
∴,,
∴,,
∴,
∴,
∴,
∴,
∵,
∴,
∴PO+PB的最小值为,
故答案为:.
三、解答题
19.证明:(1)∵四边形是矩形,
∴(矩形的对角相等),
(矩形的对边平行).
∴.
又∵,
∴.
∴;
(2)∵四边形是矩形,
∴(矩形的对边相等).
在和中,
∵,,
∴.
∴.
20.解:∵GA平分∠BAD,GB平分∠ABC,
∴∠GAB=∠BAD,∠GBA=∠ABC,
∵ ABCD中,∠DAB+∠ABC=180°,
∴∠GAB+∠GBA=(∠DAB+∠ABC)=90°,
即∠AGB=90°,
同理可得,∠DEC=90°,∠AHD=90°=∠EHG,
∴四边形EFGH是矩形.
21.解:(1)四边形ABEC是平行四边形;理由如下:
∵AD为BC边上的中线,
∴BD=CD,
∵DE=AD,
∴四边形ABEC是平行四边形(对角线互相平分的四边形是平行四边形);
(2)当∠BAC=90°,四边形ABEC是矩形;理由如下:
∵四边形ABEC是平行四边形,∠BAC=90°,
∴四边形ABEC是矩形(有一个角是直角的平行四边形是矩形).
22.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.
23.(1)证明:,
,
,
∵在矩形ABCD中,
∴,
,
,
四边形是矩形.
(2)解:∵在矩形中,,
,
.
由(1)可知,,
,
,
,
.
24.(1)∵动点P从点A开始沿边以的速度运动,
∴,
又∵,
∴.
故答案为:;
(2)∵四边形是矩形,
∴,
由题意得,, ,
当四边形为矩形时,,
∴,
∴.
(3)当时,如图1,过点Q作于E,
∴,,
当时,,
∴,
解得:;
当时,如图2,过点Q作于E,
∴,
当时,,
∴,
解得:;
∴或9.
25.(1)解:∵,
∴,
∵四边形为矩形,
∴,,
.
∵,
,
,
;
(2)证明:如图,延长交于点M,
在矩形中,,
∴,
∴E点为的中点,
∴,
,
,
,
∴,
∴C是的中点,
∵,
.
(3)解:如图,连接,
∵,,
∴,
,
∴,,
∴.
26.(1)连接,如图①,
∵是的中点,
∴,
∵沿折叠后,得到,
∴,,
∴,
∴,
在和中,
,
∴,
∴;
设,则,
在中,,
∴,
解得,,
即;
(2)延长交的延长线于点,如图②,
∵四边形是平行四边形,
∴,
∴,
∵是的中点,
∴,
又,
∴,
∴,
由折叠得,
∴,,
∴
∴,即;
(3)如图③,在中,,
即,
由折叠得,,
∴,
设,则,
在中,,
即,
解得,,
即.
故答案为:.
27.(1)证明:∵四边形是矩形,
∴,
∴,
由折叠得,
∴,
∴;
(2)解:由折叠得,,
∴的周长为,
如图1,连接,,
∵,
∴当点恰好位于对角线上时,最小,
在中,由勾股定理得,
∴的最小值为,
∴周长的最小值为;
(3)解:与HG的数量关系是,理由如下:
如图2,由折叠可知,,,过点作,交于点.
∵,
∴,
∴,
∴,
∴点是的中点,
∵,即,
∴,
∵,
∴.
∴.
∴.
∵点为中点,点是中点,
∴,.
∴.
∴,
∴.
一、单选题
1.下列性质中,矩形具有而一般平行四边形不具有的是( ).
A.对边相等 B.对角相等 C.对角线相等 D.对边平行
2.如图,矩形ABCD的对角线,则BD的长为( )
A.3cm B.4cm C.5cm D.6cm
3.如图,矩形的对角线、相交于点,,,则矩形的对角线长为( )
A. B. C. D.
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
5.在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是( )
A.AB=CD,AD=BC,AC=BD B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,AC⊥BD D.∠A=∠B=90°,AC=BD
6.已知四边形ABCD的对角线相交于点O,且OA=OB=OC=OD,那么这个四边形是( )
A.是中心对称图形,但不是轴对称图形 B.是轴对称图形,但不是中心对称图形
C.既是中心对称图形,又是轴对称图形 D.既不是中心对称图形,又不是轴对称图形
7.如图,在平行四边形中,、是上两点,,连接、、、,添加一个条件,使四边形是矩形,这个条件是( )
A. B. C. D.
8.如图,在矩形中,,对角线与相交于点O,垂直平分于点E,则的长为( )
A. B. C.4 D.2
9.如图,在矩形中,,E是的中点,于点F,则的长是( )
A.1 B. C. D.2
10.如图,在矩形ABCD中,以对角线AC为斜边作Rt△AEC,过点E作EF⊥DC于点F,连结AF,若AD=DF,S△AEF=3,S△ACF=5,则矩形ABCD的面积为( )
A.18 B.19 C.20 D.21
二、填空题
11.矩形的两条对角线的夹角为,较短的边长为,则对角线长为 .
12.如图,矩形ABCD中,AC、BD相交于点O且AC=12,如果∠AOD=60°,则DC= .
13.如图,在矩形ABCD中,,,平分,,则 .
14.矩形ABCD中,对角线AC=10㎝,两邻边长度之比AB:BC是3:4,那么= ㎝ .
15.四边形中,交于O,给出条件①;②;③;④.其中能推得四边形是矩形的是(填序号) .
16.如图,延长矩形的边至点,使,若,则 .
17.如图,在矩形中,点E在边上,沿折叠得到,且点B,F,E三点共线,连接,若,,则 , .
18.如图,矩形的对角线相交于点O,,,点在对角线上,P是的中点,的最小值是 .
三、解答题
19.已知:如图,四边形是矩形,,对角线与相交于点O.
求证:
(1);
(2).
20.如图 ABCD,四个内角的平分线相交于E、F、G、H四个点;
求证:四边形EFGH是矩形.
21.如图,在中,为边上的中线,延长至E,使,连接,.
(1)试判断四边形的形状;
(2)当满足什么条件时,四边形是矩形?
22.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠DAB,CF=3,BF=4,求DF长.
23.如图,矩形ABCD的对角线相交于点,且.
(1)求证:四边形是矩形;
(2)点在上,连接,若,求的面积.
24.如图,在矩形中,,,动点P从点A开始沿边以的速度运动,动点Q从点C开始沿边以的速度运动.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动.设动点的运动时间为.
(1)用含t的代数式表示 ;
(2)若四边形为矩形,求t的值;
(3)是否存在t值,使线段的长为?若存在,直接写出t的值;若不存在,说明理由.
25.如图,在矩形中,是边上一点,连接,过点作交于点,连接.
(1)如图1,若,求证:.
(2)如图2,若恰好是边的中点,求证:.
(3)在(2)的条件下,当,时,求的值.
26.如图,在矩形中,,,点E是上一点.将沿折叠后,得到.点F在矩形内部,延长交于点G.
(1)如图①,当点E是中点时,求的长;
(2)如图②,在(1)的条件下,当矩形变化为平行四边形时,求证:;
(3)如图③,在矩形中,当点F落在矩形对角线上时,的长是
27.如图1,点是矩形边上一点(不与点,重合),直线与的延长线交于点.将沿直线折叠得到,点在矩形的内部,延长交直线于点.
(1)证明:;
(2)如图2,连接,若,,求周长的最小值;
(3)如图3,连接交于点,点是的中点,当时,请判断与的数量关系,并说明理由.
答案
一、单选题
1.C
【分析】由矩形的性质和平行四边形的性质即可得出结论.
【解析】解:∵矩形的对边相等,对角相等,对角线互相平分且相等;
平行四边形的对边相等,对角相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选C.
2.D
【分析】根据矩形的性质可知AC=BD且AO=CO,根据AO=3,求出AC,进一步求BD即可.
【解析】解:∵四边形ABCD是矩形,
∴AC=BD,AO=OC,
∵AO=3cm,
∴AC=2AO=6cm,
∴BD=6cm.
故选:D.
3.C
【分析】根据矩形性质得出,,,,推出,求出等边三角形,求出,即可得出答案.
【解析】,
,
四边形是矩形,
,,,,
,
,
是等边三角形,
,
,
,.
故选C.
4.B
【分析】根据矩形的性质可得OA=OD,从而得到∠ADO=55°,再由,即可求解.
【解析】解:在矩形ABCD中,OA=OD,
∴∠ADO=∠DAO,
∵∠AOB=∠ADO+∠DAO,,
∴∠ADO=55°,
∵,即∠AED=90°,
∴∠DAE=35°.
故选:B
5.C
【解析】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,
∴A正确;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
又,
∴四边形ABCD是矩形,
∴B正确;
∵∠A=∠C,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴C不正确;
如图所示:
在和中,
∴BC=AD,
∴四边形ABCD是平行四边形,
又 ∴四边形ABCD是矩形,
∴D正确;
故选:C
6.C
【分析】先根据已知条件OA=OB=OC=OD,可知四边形ABCD的对角线相等且互相平分,得出四边形ABCD是矩形,然后根据矩形的对称性,得出结果.
【解析】解:如图所示:
∵四边形ABCD的对角线相交于点O且OA=OB=OC=OD,
∴OA=OC,OB=OD;AC=BD,
∴四边形ABCD是矩形,
∴四边形ABCD既是轴对称图形,又是中心对称图形.
故选:C.
7.A
【分析】由平行四边形的性质可知:,,再证明即可证明四边形是平行四边形.
【解析】∵四边形是平行四边形,
∴,,
∵对角线上的两点、满足,
∴,即,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形.
故选:A.
8.B
【分析】此题考查了矩形的性质、线段垂直平分线的性质以及勾股定理,由矩形的性质和线段垂直平分线的性质证出,得出,由勾股定理求出即可.
【解析】解:∵四边形是矩形,
∴,,,
∴,
∵垂直平分,
∴,
∵,
∴,
∴,
故选:B.
9.C
【分析】延长交于点M,可证得,从而得到,进而得到,再由直角三角形的性质,即可求解.
【解析】解:如图,延长交于点M,
∵E是的中点,
∴,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∴,
∵,即,
∴,
故选:C
10.B
【分析】过点E作EG垂直AD延长线于点G,然后通过已知三角形的面积得到EF和FC的比值,从而设EF和FC的长度分别为3b和5b,AD和DF的长度为a,然后利用Rt△GEA,Rt△EFC,Rt△CEA,Rt△DAC中的勾股定理得到a与b的关系,再利用△AEF的面积求出a和b的值,最后求矩形ABCD的面积.
【解析】解:过点E作EG⊥AD交AD的延长线与G
∵EF⊥DC
∴ ,
∵DF=AD
∴EF:CF=3∶5
设EF=3b,CF=5b,AD=DF=a
∵∠G=90°,∠EFD=90°,∠GDF=90°
∴四边形EFDG是矩形
∴GE=DF=a,GD=EF=3b
在Rt△GEA中,
在Rt△EFC中,
在Rt△CEA中,
∴
=
=
在Rt△DAC中,
∴=
∴
∵b>0
∴
∴
∴
∴a=
∴
故选:B.
二、填空题
11.24
【分析】根据矩形对角线相等且互相平分性质和题中条件得△AOB为等边三角形,即可得到矩形对角线一半长,进而求解即可.
【解析】解:如图所示,
∵四边形ABCD是矩形,AC,BD是对角线,
∴AC=BD,
OA=OB=OD=OC=BD=AC,
在△AOB中,OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
OA=OB=AB=12cm,
则BD=2OB=2×12=24(cm),
故答案为24.
12.
【分析】根据矩形的对角线互相平分且相等可得OA=OD,然后判断出△AOD是等边三角形,再根据勾股定理解答即可.
【解析】解:∵四边形ABCD是矩形,
∴OA=OD=AC=×12=6,∠ADC=90°,
∵∠AOD=60°,
∴△AOD是等边三角形,
∴AD=OA=6,
∴.
故答案为:.
13.1.5.
【分析】根据题意画出图形,由题意得出△CDF是等腰直角三角形即可得出DF的长,从而得出AF.
【解析】由题意画出图形如下:
∵ABCD是矩形,
∴AD=BC=5cm,CD=AB=3.5cm,
∵AE平分∠BAD,CF∥AE,
∴△ABE和△CDF是等腰直角三角形,
∴DF=CD=3.5cm,
∴AF=AD-AF=1.5cm.
故答案为:1.5.
14.48
【分析】根据题意,画出图形,设AB=3xcm,BC=4xcm,根据勾股定理列出方程即可求出x,从而求出AB和BC,最后根据矩形的面积公式计算即可.
【解析】解:如下图所示,设AB=3xcm,BC=4xcm,
根据勾股定理AB2+BC2=AC2
即,
解得:x=2或-2(不符合实际,舍去)
∴AB=6cm,BC=8cm
∴=cm2
故答案为:48.
15.③
【分析】由矩形的判定、平行四边形的判定与性质分别对各个选项进行判断即可.
【解析】①∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,不符合题意;
②,
不能判定四边形ABCD是矩形,不符合题意;
③∵OA=OB=OC=OD,
∴四边形ABCD是平行四边形,
∴AC=BD,
∴平行四边形ABCD是矩形,符合题意;
④,
不能推出四边形ABCD是矩形,不符合题意;
故答案为:③.
16.15°
【分析】连接AC,由矩形性质可得∠E=∠DAE、BD=AC=CE,知∠E=∠CAE,而∠ADB=∠CAD=30°,可得∠E度数.
【解析】解:连接AC,
∵四边形ABCD是矩形,
∴AC=BD,AD=AD,AB=CD,
∴△ABD≌△DCA,
∴∠ADB=∠CAD=30°,
∵AD∥BE,
∴∠E=∠DAE,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠CAD=∠CAE+∠DAE,
∴∠E+∠E=30°,即∠E=15°,
故答案为:15°.
17.
【分析】本题考查勾股定理,矩形的性质,折叠的性质,掌握矩形的性质是解题的关键.设交于H,,,根据勾股定理得到,,解得,,然后根据三角形的面积求出解题即可.
【解析】解:设交于H,如图:
设,,
∵沿折叠得到,
∴,,
∵,
∴,
在中,,
∴①,
在中,,
∴②,
①②联立解得,或(舍去),
∴,,
∴;
,
∵沿折叠得到,
∴,,
∴,
∴,
∴;
故答案为:,.
18.
【分析】此题重点考查矩形的性质、轴对称的性质、等边三角形的判定与性质、三角形的中位线定理、直角三角形中30°角所对的直角边等于斜边的一半、勾股定理、两点之间线段最短等知识,正确地作出所需要的辅助线是解题的关键.取的中点F,再作B关于的对称点H,与交于点G,连接,求出,再利用三角形的三边关系可得答案.
【解析】解:取的中点F,作直线,
∵点P是的中点,
∴,
∴,
作点B关于直线的对称点H,连接交直线于点G,连接,
∵垂直平分,
∴,,
∵四边形是矩形,,
∴,,,,
∴,
∵,
∴,
∴是等边三角形,
∴,,
∴,,
∴,
∴,
∴,
∴,
∵,
∴,
∴PO+PB的最小值为,
故答案为:.
三、解答题
19.证明:(1)∵四边形是矩形,
∴(矩形的对角相等),
(矩形的对边平行).
∴.
又∵,
∴.
∴;
(2)∵四边形是矩形,
∴(矩形的对边相等).
在和中,
∵,,
∴.
∴.
20.解:∵GA平分∠BAD,GB平分∠ABC,
∴∠GAB=∠BAD,∠GBA=∠ABC,
∵ ABCD中,∠DAB+∠ABC=180°,
∴∠GAB+∠GBA=(∠DAB+∠ABC)=90°,
即∠AGB=90°,
同理可得,∠DEC=90°,∠AHD=90°=∠EHG,
∴四边形EFGH是矩形.
21.解:(1)四边形ABEC是平行四边形;理由如下:
∵AD为BC边上的中线,
∴BD=CD,
∵DE=AD,
∴四边形ABEC是平行四边形(对角线互相平分的四边形是平行四边形);
(2)当∠BAC=90°,四边形ABEC是矩形;理由如下:
∵四边形ABEC是平行四边形,∠BAC=90°,
∴四边形ABEC是矩形(有一个角是直角的平行四边形是矩形).
22.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形BFDE是矩形,
∴∠BFD=90°,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∵AB∥DC,
∴∠DFA=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵AD=BC,
∴DF=BC,
∴DF=5.
23.(1)证明:,
,
,
∵在矩形ABCD中,
∴,
,
,
四边形是矩形.
(2)解:∵在矩形中,,
,
.
由(1)可知,,
,
,
,
.
24.(1)∵动点P从点A开始沿边以的速度运动,
∴,
又∵,
∴.
故答案为:;
(2)∵四边形是矩形,
∴,
由题意得,, ,
当四边形为矩形时,,
∴,
∴.
(3)当时,如图1,过点Q作于E,
∴,,
当时,,
∴,
解得:;
当时,如图2,过点Q作于E,
∴,
当时,,
∴,
解得:;
∴或9.
25.(1)解:∵,
∴,
∵四边形为矩形,
∴,,
.
∵,
,
,
;
(2)证明:如图,延长交于点M,
在矩形中,,
∴,
∴E点为的中点,
∴,
,
,
,
∴,
∴C是的中点,
∵,
.
(3)解:如图,连接,
∵,,
∴,
,
∴,,
∴.
26.(1)连接,如图①,
∵是的中点,
∴,
∵沿折叠后,得到,
∴,,
∴,
∴,
在和中,
,
∴,
∴;
设,则,
在中,,
∴,
解得,,
即;
(2)延长交的延长线于点,如图②,
∵四边形是平行四边形,
∴,
∴,
∵是的中点,
∴,
又,
∴,
∴,
由折叠得,
∴,,
∴
∴,即;
(3)如图③,在中,,
即,
由折叠得,,
∴,
设,则,
在中,,
即,
解得,,
即.
故答案为:.
27.(1)证明:∵四边形是矩形,
∴,
∴,
由折叠得,
∴,
∴;
(2)解:由折叠得,,
∴的周长为,
如图1,连接,,
∵,
∴当点恰好位于对角线上时,最小,
在中,由勾股定理得,
∴的最小值为,
∴周长的最小值为;
(3)解:与HG的数量关系是,理由如下:
如图2,由折叠可知,,,过点作,交于点.
∵,
∴,
∴,
∴,
∴点是的中点,
∵,即,
∴,
∵,
∴.
∴.
∴.
∵点为中点,点是中点,
∴,.
∴.
∴,
∴.
