人教版七年级数学上册试题 第一章 有理数章节复习卷(含解析)
文档属性
| 名称 | 人教版七年级数学上册试题 第一章 有理数章节复习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-11 14:51:03 | ||
图片预览




文档简介
第一章 有理数(章节复习卷)
一、单选题
1.下表是我国几个城市某年一月份的平均气温.其中气温最低的城市是( )
城市 北京 武汉 广州 哈尔滨
平均气温(单位:)
A.北京 B.武汉 C.广州 D.哈尔滨
2.下列各式中成立的是( )
A. B.
C. D.
3.有理数a,b在数轴上对应的位置如图所示,则正确的( )
A. B. C. D.
4.下列说法中,正确的是( )
A.0是绝对值最小的整数 B.互为相反数的两个数之积为1
C.有理数包括正有理数和负有理数 D.一个有理数的平方总是正数
5.如图,小明在写作业时不慎将两滴墨水滴在数轴上,对于结论Ⅰ和Ⅱ,下列判断正确的是( )
结论Ⅰ:墨水遮住了绝对值不大于3的所有整数;结论Ⅱ:墨水遮住的整数之和为3
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ对Ⅱ不对 D.Ⅰ不对Ⅱ对
6.对于有理数a,b有下列几种说法:
①若a+b=0,则a与b互为相反数,②若a+b<0,则a与b异号,
③a+b>0,若a,b同号,则ab>0,④若|a|>|b|,且a,b同号,则a+b>0,
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
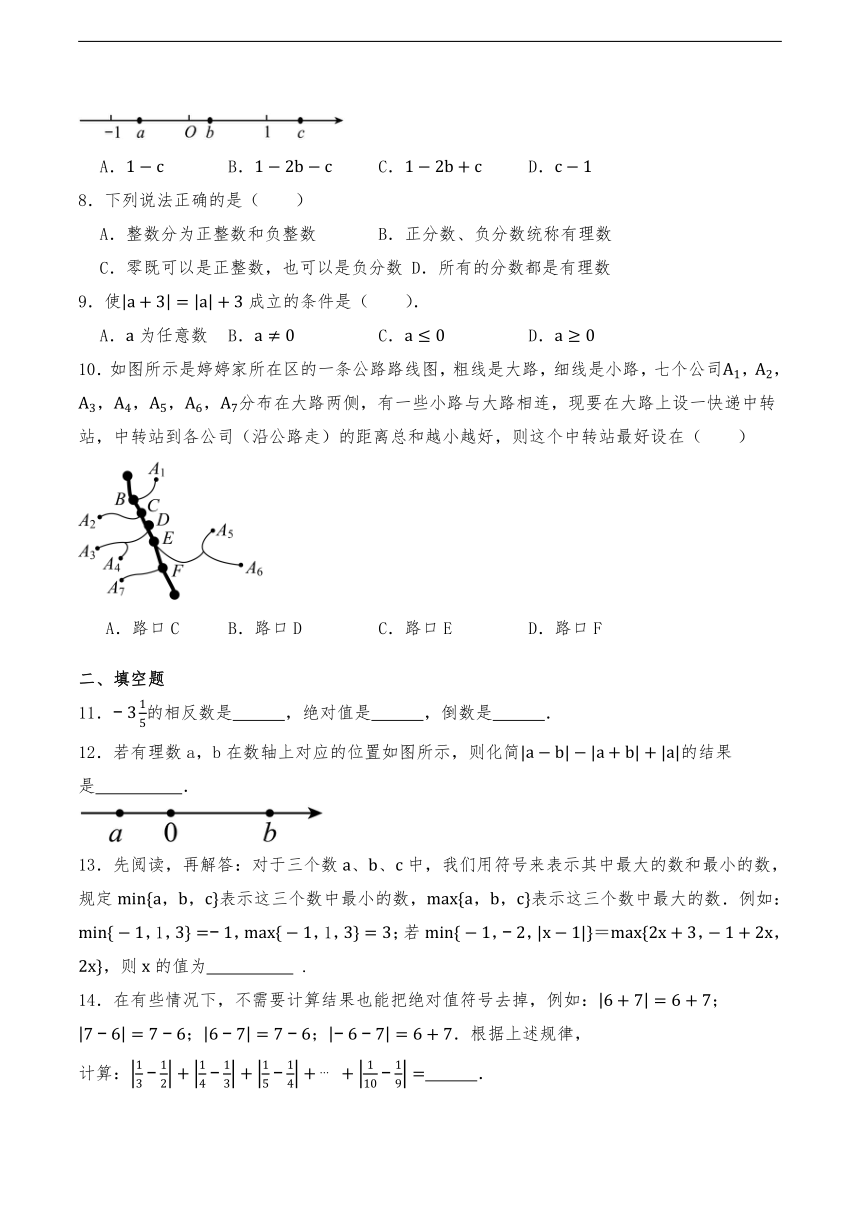
7.有理数在数轴上的位置如图所示.则式子的值是( )
A. B. C. D.
8.下列说法正确的是( )
A.整数分为正整数和负整数 B.正分数、负分数统称有理数
C.零既可以是正整数,也可以是负分数 D.所有的分数都是有理数
9.使成立的条件是( ).
A.为任意数 B. C. D.
10.如图所示是婷婷家所在区的一条公路路线图,粗线是大路,细线是小路,七个公司,,,,,,分布在大路两侧,有一些小路与大路相连,现要在大路上设一快递中转站,中转站到各公司(沿公路走)的距离总和越小越好,则这个中转站最好设在( )
A.路口C B.路口D C.路口E D.路口F
二、填空题
11.的相反数是 ,绝对值是 ,倒数是 .
12.若有理数a,b在数轴上对应的位置如图所示,则化简的结果是 .
13.先阅读,再解答:对于三个数、、中,我们用符号来表示其中最大的数和最小的数,规定,,表示这三个数中最小的数,,,表示这三个数中最大的数.例如:,1,,,1,;若,,=,,,则的值为 .
14.在有些情况下,不需要计算结果也能把绝对值符号去掉,例如:;
;;.根据上述规律,
计算: .
15.若的相反数为2,且.则 .
16.如果,且,那么 .
三、解答题
17.若,.
(1)若,求的值;
(2)若,求的值.
18.数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,若x为整数,此时x的取值是 ;
(3)已知|x+1|+|x﹣2|=7时,x的取值是 .
19.画出数轴,在数轴上表示下列各数,并按从小到大用“”把这些数连接起来.
,,,,,.
20.画出数轴,在数轴上表示下列各数,并用“<”连接.
+5,,,,,0
21.七年级2班的3位同学一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点,表示的数都是绝对值为5的数,且点在点在左侧”;
乙说:“点表示负整数且到原点的距离为3,点表示正整数,且,这两个点所表示的数的差是4”;
丙说:“点表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,判断:表示__________;表示__________;表示__________;表示__________;表示__________;
(2)请你画出一条数轴,并在数轴上描出,,,,五个不同的点.
22.在数轴上画出表示下列各数的点:.再将这些数重新排成一行,并用“<”号把它们连接起来.
23.小强早晨跑步,他从自己家出发,向东跑了2km到达小兵家,继续向东跑了1.5km到达小颖家,然后又向西跑了4.5km到达学校,最后又向东跑回到自己家.
(1)以小强家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小兵家,用点B表示出小颖家,用点C表示出学校的位置;
(2)求小兵家与学校之间的距离;
(3)如果小强跑步的速度是250,那么小强跑步一共用了多长时间?
24.如图,点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为,在数轴上A、B两点之间的距离.回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_______,表示和3的两点之间的距离是________.
(2)设点P在数轴上对应的数为x,若,则________.
(3)数轴上表示x和的两点之间的距离为______________.
(4)当整数_________________时,代数式有最小值为________.
(5)当x取何值时,代数式的值等于8 ?(写出过程)
参考答案
一、单选题
1.D
【分析】本题考查了有理数的大小比较,熟练掌握有理数大小比较的法则是解本题的关键.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的反而小.
【详解】解:∵,
∴平均气温最低的城市是哈尔滨.
故选:D.
2.D
【分析】化简有理数的多重符号及化简绝对值解题即可.
【详解】解:A选项,故错误,
B选项,左右不相等,错误,
C选项,故错误,
D选项,故正确,
故选D.
3.D
【分析】本题主要考查了有理数与数轴,根据数轴可得,据此逐一判断即可得到答案.
【详解】解:由数轴可知,,
∴,,
故选:D.
4.A
【分析】本题主要考查了有理数的分类,正负数的概念,相反数和绝对值的意义,根据相关基础知识逐项判断即可.
【详解】解:A、0是绝对值最小的整数,也是绝对值最小的有理数,故本选项符合题意;
B、互为倒数的两个数之积为1,互为相反数的两个数之积是非正数,一定不为1,故本选项不符合题意;
C、有理数包括正有理数和负有理数以及0,故本选项不符合题意;
D、0的平方还是0,不是正数,故本选项不符合题意.
故选A.
5.D
【分析】本题考查了数轴,熟练掌握数轴三要素以及当数轴方向朝右时,右边的数总比左边的大是解题的关键.根据数轴的定义即可得到答案.
【详解】解:依题意得:墨水遮住的部分
故墨水没有遮住-3,所以墨水遮住了绝对值不大于3的所有整数的说法错误,结论Ⅰ错误,
墨水遮住的整数有,整数之和为3,;结论Ⅱ正确.
故选:D
6.B
【分析】①根据相反数的意义:只有符合不同的两个数互为相反数,进行判断即可.
【详解】解:①若a+b=0,则a=-b,即a与b互为相反数,本选项正确;
②若a+b<0,若a=-1,b=-2,a+b=-3<0,但是a与b同号,本选项错误;
③a+b>0,若a与b同号,只有同时为正,故ab>0,本选项正确;
④若|a|>|b|,且a,b同号,例如a=-3,b=-2,满足条件,但是a+b=-5<0,本选项错误.
则正确的结论有2个.
故选:B.
7.A
【分析】本题考查数轴、化简绝对值、整式的加减,先根据数轴得到,进而得到,,,然后化简绝对值和整式的加减求解即可.
【详解】解:由数轴得,
∴,,,
∴
,
故选:A.
8.D
【分析】按有理数的分类解答即可.
【详解】解:、正整数、0、负整数统称为整数,故本选项错误;
、正分数、负分数统称为分数,故本选项错误;
、零既不是正数也不是负数,故本选项错误;
、所有的分数都是有理数,故本选项正确;
故选:D.
9.D
【分析】分,,三种情况,结合绝对值的意义化简绝对值,看等号是否恒成立,从而得出答案.
本题主要考查了含绝对值符号的等式.解决问题的关键是熟练掌握绝对值的化简,分类讨论.
【详解】当时,
,,
等式化为:,
成立;
当时,
,,
等式化为:,
解得:,
不符合题意;
当时,
,,
等式化为:,
矛盾.
故使成立的条件是:.
故选:D.
10.B
【分析】本题主要考查了实际问题中的大小比较,列代数式,整式的加减,根据给定图形,用表示个公司沿小公路到大公路的最近距离之和,,再求出到路口,,,的距离总和,比较大小作答.
【详解】解∶观察图形知,七个公司要到中转站,先都必须沿小公路走到小公路与大公路的连接点,
令到、到、到、到、到、到、到的小公路距离总和为, , , , ,
路口为中转站时,距离总和.
路口为中转站时,距离总和.
路口为中转站时,距离总和 .
路口为中转站时,距离总和,
∴,
∴这个中转站最好设在路口.
故选∶ B.
二、填空题
11.
【分析】根据相反数的性质,互为相反数的两个数和为0;绝对值的定义,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0;倒数的性质,互为倒数的两个数积为1,求解即可.
【详解】解:∵互为相反数的两个数和为0,
的相反数是;
∵一个负数的绝对值是它的相反数,
的绝对值是;
∵互为倒数的两个数积为1,
的倒数是,
故答案为:,,.
12.-3a
【分析】根据数轴可判断,且,进而可判断,,由此化简绝对值即可.
【详解】由数轴可知,且,
∴,,
∴
.
故答案为:-3a.
13.
【分析】根据题意可知:,﹣2,,表示最小的数是﹣2,max{2x+3,﹣1+2x,2x}表示最大的数是2x+3,列方程,解方程可得的值.
【详解】解:∵﹣2<﹣1<,
∴,﹣2,,=﹣2,
∵﹣1+2x<2x<2x+3,
∴max{2x+3,﹣1+2x,2x}=2x+3,
∵,﹣2,,=max{2x+3,﹣1+2x,2x},
∴2x+3=﹣2,
解得:x=,
故答案为:.
14.
【分析】此题主要考查了绝对值的化简,有理数的加减运算,根据绝对值的性质:正数绝对值等于它本身,负数绝对值等于它的相反数,进行计算即可,解题关键是熟练掌握绝对值的性质.
【详解】解:
,
故答案为:.
15.
【分析】本题考查代数式求值,涉及绝对值运算、相反数定义等知识,根据题中条件求出值,代值求解即可得到答案,熟记绝对值及相反数定义是解决问题的关键.
【详解】解:∵的相反数为2,
∴,
∵,
∴,
∴,
故答案为:.
16.或
【分析】由题意可求出,故可分类讨论:①当时,则,从而可化简绝对值求解;②当时,则,同理求解即可.
【详解】解:,且,
.
对的值分类讨论如下:
①当时,
,
,
;
②当时,
,
,
.
故答案为:或.
三、解答题
17.(1)解:∵,,
∴,
又∵,
∴;
①当时,;
②当时,.
综上,的值为或.
(2)解:∵,
∴,
∴,
∴;
①当时,;
②当时,.
综上,的值为8或4.
18.解:(1)①∵数轴上两点A、B表示的数为x、﹣1,
A、B之间的距离可用含x的式子表示为|x+1|;
故答案为:|x+1|;
②依题意有|x+1|=2,
则x+1=﹣2或x+1=2,
解得:x=﹣3或x=1.
故x值为﹣3或1.
故答案为﹣3或1.
(2)当x<-1时,|x+1|+|x﹣2|=﹣x-1-x+2=-2x+1>3,
当-1≤x≤2时,|x+1|+|x﹣2|=x+1-x+2=3,
当x>2时,|x+1|+|x﹣2|=x+1+x-2=2x-1>3,
∴|x+1|+|x﹣2|的最小值为3,此时x的取值是﹣1≤x≤2;
故答案为3;﹣1≤x≤2;
(3)当x<﹣1时,- x-1-x+2=7,
-2x=6,
x=-3,
当-1≤x≤2时,x+1-x+2=7,
得3=7不成立,
当x>2时,x+1+ x﹣2=7.
2 x =8,
解得x =4,
综上所述,x的取值是﹣3或4.
故答案为:﹣3或4.
19.解:如图所示:
.
20.解:,,,
数轴表示如下所示:
∴.
21.(1)解:由甲的描述可得,点所表示的数为,点所表示的数为5,
由乙的描述可得,点所表示的数为,点所表示的数为1,
由丙的描述可得,点所表示的数为0,
故答案为:,5,,1,0;
(2)解:在数轴上表示如图所示:
22.解:,
在数轴上表示各数如下:
用“<”号把它们连接如下:
23.
解:(1)根据题意得:小兵家的位置对应的数为2,小颖家的位置对应的数为3.5,学校的位置对应的数为-1,如图所示:
(2).
答:小兵家与学校之间的距离是3km.
(3),,.
答:小强跑步一共用了36min.
24.(1)数轴上表示2和5两点之间的距离是:,数轴上表示和的两点之间的距离是:;
故答案为:3,4.
(2),
∴,
∴,
故答案为:8或.
(3)x和的两点之间的距离为,
故答案为:.
(4)∵时,
∴,
当时,;
当时,;
故当时,代数式有最小值,且为4,
故当x取整数中的一个时,代数式有最小值为4,
故答案为:0,4.
(5)∵时,
∴,不成立;
当时,;
故,
解得,符合题意;
当时,;
故
解得,符合题意;
综上,或.
一、单选题
1.下表是我国几个城市某年一月份的平均气温.其中气温最低的城市是( )
城市 北京 武汉 广州 哈尔滨
平均气温(单位:)
A.北京 B.武汉 C.广州 D.哈尔滨
2.下列各式中成立的是( )
A. B.
C. D.
3.有理数a,b在数轴上对应的位置如图所示,则正确的( )
A. B. C. D.
4.下列说法中,正确的是( )
A.0是绝对值最小的整数 B.互为相反数的两个数之积为1
C.有理数包括正有理数和负有理数 D.一个有理数的平方总是正数
5.如图,小明在写作业时不慎将两滴墨水滴在数轴上,对于结论Ⅰ和Ⅱ,下列判断正确的是( )
结论Ⅰ:墨水遮住了绝对值不大于3的所有整数;结论Ⅱ:墨水遮住的整数之和为3
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ对Ⅱ不对 D.Ⅰ不对Ⅱ对
6.对于有理数a,b有下列几种说法:
①若a+b=0,则a与b互为相反数,②若a+b<0,则a与b异号,
③a+b>0,若a,b同号,则ab>0,④若|a|>|b|,且a,b同号,则a+b>0,
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
7.有理数在数轴上的位置如图所示.则式子的值是( )
A. B. C. D.
8.下列说法正确的是( )
A.整数分为正整数和负整数 B.正分数、负分数统称有理数
C.零既可以是正整数,也可以是负分数 D.所有的分数都是有理数
9.使成立的条件是( ).
A.为任意数 B. C. D.
10.如图所示是婷婷家所在区的一条公路路线图,粗线是大路,细线是小路,七个公司,,,,,,分布在大路两侧,有一些小路与大路相连,现要在大路上设一快递中转站,中转站到各公司(沿公路走)的距离总和越小越好,则这个中转站最好设在( )
A.路口C B.路口D C.路口E D.路口F
二、填空题
11.的相反数是 ,绝对值是 ,倒数是 .
12.若有理数a,b在数轴上对应的位置如图所示,则化简的结果是 .
13.先阅读,再解答:对于三个数、、中,我们用符号来表示其中最大的数和最小的数,规定,,表示这三个数中最小的数,,,表示这三个数中最大的数.例如:,1,,,1,;若,,=,,,则的值为 .
14.在有些情况下,不需要计算结果也能把绝对值符号去掉,例如:;
;;.根据上述规律,
计算: .
15.若的相反数为2,且.则 .
16.如果,且,那么 .
三、解答题
17.若,.
(1)若,求的值;
(2)若,求的值.
18.数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,若x为整数,此时x的取值是 ;
(3)已知|x+1|+|x﹣2|=7时,x的取值是 .
19.画出数轴,在数轴上表示下列各数,并按从小到大用“”把这些数连接起来.
,,,,,.
20.画出数轴,在数轴上表示下列各数,并用“<”连接.
+5,,,,,0
21.七年级2班的3位同学一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点,表示的数都是绝对值为5的数,且点在点在左侧”;
乙说:“点表示负整数且到原点的距离为3,点表示正整数,且,这两个点所表示的数的差是4”;
丙说:“点表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,判断:表示__________;表示__________;表示__________;表示__________;表示__________;
(2)请你画出一条数轴,并在数轴上描出,,,,五个不同的点.
22.在数轴上画出表示下列各数的点:.再将这些数重新排成一行,并用“<”号把它们连接起来.
23.小强早晨跑步,他从自己家出发,向东跑了2km到达小兵家,继续向东跑了1.5km到达小颖家,然后又向西跑了4.5km到达学校,最后又向东跑回到自己家.
(1)以小强家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小兵家,用点B表示出小颖家,用点C表示出学校的位置;
(2)求小兵家与学校之间的距离;
(3)如果小强跑步的速度是250,那么小强跑步一共用了多长时间?
24.如图,点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为,在数轴上A、B两点之间的距离.回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_______,表示和3的两点之间的距离是________.
(2)设点P在数轴上对应的数为x,若,则________.
(3)数轴上表示x和的两点之间的距离为______________.
(4)当整数_________________时,代数式有最小值为________.
(5)当x取何值时,代数式的值等于8 ?(写出过程)
参考答案
一、单选题
1.D
【分析】本题考查了有理数的大小比较,熟练掌握有理数大小比较的法则是解本题的关键.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的反而小.
【详解】解:∵,
∴平均气温最低的城市是哈尔滨.
故选:D.
2.D
【分析】化简有理数的多重符号及化简绝对值解题即可.
【详解】解:A选项,故错误,
B选项,左右不相等,错误,
C选项,故错误,
D选项,故正确,
故选D.
3.D
【分析】本题主要考查了有理数与数轴,根据数轴可得,据此逐一判断即可得到答案.
【详解】解:由数轴可知,,
∴,,
故选:D.
4.A
【分析】本题主要考查了有理数的分类,正负数的概念,相反数和绝对值的意义,根据相关基础知识逐项判断即可.
【详解】解:A、0是绝对值最小的整数,也是绝对值最小的有理数,故本选项符合题意;
B、互为倒数的两个数之积为1,互为相反数的两个数之积是非正数,一定不为1,故本选项不符合题意;
C、有理数包括正有理数和负有理数以及0,故本选项不符合题意;
D、0的平方还是0,不是正数,故本选项不符合题意.
故选A.
5.D
【分析】本题考查了数轴,熟练掌握数轴三要素以及当数轴方向朝右时,右边的数总比左边的大是解题的关键.根据数轴的定义即可得到答案.
【详解】解:依题意得:墨水遮住的部分
故墨水没有遮住-3,所以墨水遮住了绝对值不大于3的所有整数的说法错误,结论Ⅰ错误,
墨水遮住的整数有,整数之和为3,;结论Ⅱ正确.
故选:D
6.B
【分析】①根据相反数的意义:只有符合不同的两个数互为相反数,进行判断即可.
【详解】解:①若a+b=0,则a=-b,即a与b互为相反数,本选项正确;
②若a+b<0,若a=-1,b=-2,a+b=-3<0,但是a与b同号,本选项错误;
③a+b>0,若a与b同号,只有同时为正,故ab>0,本选项正确;
④若|a|>|b|,且a,b同号,例如a=-3,b=-2,满足条件,但是a+b=-5<0,本选项错误.
则正确的结论有2个.
故选:B.
7.A
【分析】本题考查数轴、化简绝对值、整式的加减,先根据数轴得到,进而得到,,,然后化简绝对值和整式的加减求解即可.
【详解】解:由数轴得,
∴,,,
∴
,
故选:A.
8.D
【分析】按有理数的分类解答即可.
【详解】解:、正整数、0、负整数统称为整数,故本选项错误;
、正分数、负分数统称为分数,故本选项错误;
、零既不是正数也不是负数,故本选项错误;
、所有的分数都是有理数,故本选项正确;
故选:D.
9.D
【分析】分,,三种情况,结合绝对值的意义化简绝对值,看等号是否恒成立,从而得出答案.
本题主要考查了含绝对值符号的等式.解决问题的关键是熟练掌握绝对值的化简,分类讨论.
【详解】当时,
,,
等式化为:,
成立;
当时,
,,
等式化为:,
解得:,
不符合题意;
当时,
,,
等式化为:,
矛盾.
故使成立的条件是:.
故选:D.
10.B
【分析】本题主要考查了实际问题中的大小比较,列代数式,整式的加减,根据给定图形,用表示个公司沿小公路到大公路的最近距离之和,,再求出到路口,,,的距离总和,比较大小作答.
【详解】解∶观察图形知,七个公司要到中转站,先都必须沿小公路走到小公路与大公路的连接点,
令到、到、到、到、到、到、到的小公路距离总和为, , , , ,
路口为中转站时,距离总和.
路口为中转站时,距离总和.
路口为中转站时,距离总和 .
路口为中转站时,距离总和,
∴,
∴这个中转站最好设在路口.
故选∶ B.
二、填空题
11.
【分析】根据相反数的性质,互为相反数的两个数和为0;绝对值的定义,一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0;倒数的性质,互为倒数的两个数积为1,求解即可.
【详解】解:∵互为相反数的两个数和为0,
的相反数是;
∵一个负数的绝对值是它的相反数,
的绝对值是;
∵互为倒数的两个数积为1,
的倒数是,
故答案为:,,.
12.-3a
【分析】根据数轴可判断,且,进而可判断,,由此化简绝对值即可.
【详解】由数轴可知,且,
∴,,
∴
.
故答案为:-3a.
13.
【分析】根据题意可知:,﹣2,,表示最小的数是﹣2,max{2x+3,﹣1+2x,2x}表示最大的数是2x+3,列方程,解方程可得的值.
【详解】解:∵﹣2<﹣1<,
∴,﹣2,,=﹣2,
∵﹣1+2x<2x<2x+3,
∴max{2x+3,﹣1+2x,2x}=2x+3,
∵,﹣2,,=max{2x+3,﹣1+2x,2x},
∴2x+3=﹣2,
解得:x=,
故答案为:.
14.
【分析】此题主要考查了绝对值的化简,有理数的加减运算,根据绝对值的性质:正数绝对值等于它本身,负数绝对值等于它的相反数,进行计算即可,解题关键是熟练掌握绝对值的性质.
【详解】解:
,
故答案为:.
15.
【分析】本题考查代数式求值,涉及绝对值运算、相反数定义等知识,根据题中条件求出值,代值求解即可得到答案,熟记绝对值及相反数定义是解决问题的关键.
【详解】解:∵的相反数为2,
∴,
∵,
∴,
∴,
故答案为:.
16.或
【分析】由题意可求出,故可分类讨论:①当时,则,从而可化简绝对值求解;②当时,则,同理求解即可.
【详解】解:,且,
.
对的值分类讨论如下:
①当时,
,
,
;
②当时,
,
,
.
故答案为:或.
三、解答题
17.(1)解:∵,,
∴,
又∵,
∴;
①当时,;
②当时,.
综上,的值为或.
(2)解:∵,
∴,
∴,
∴;
①当时,;
②当时,.
综上,的值为8或4.
18.解:(1)①∵数轴上两点A、B表示的数为x、﹣1,
A、B之间的距离可用含x的式子表示为|x+1|;
故答案为:|x+1|;
②依题意有|x+1|=2,
则x+1=﹣2或x+1=2,
解得:x=﹣3或x=1.
故x值为﹣3或1.
故答案为﹣3或1.
(2)当x<-1时,|x+1|+|x﹣2|=﹣x-1-x+2=-2x+1>3,
当-1≤x≤2时,|x+1|+|x﹣2|=x+1-x+2=3,
当x>2时,|x+1|+|x﹣2|=x+1+x-2=2x-1>3,
∴|x+1|+|x﹣2|的最小值为3,此时x的取值是﹣1≤x≤2;
故答案为3;﹣1≤x≤2;
(3)当x<﹣1时,- x-1-x+2=7,
-2x=6,
x=-3,
当-1≤x≤2时,x+1-x+2=7,
得3=7不成立,
当x>2时,x+1+ x﹣2=7.
2 x =8,
解得x =4,
综上所述,x的取值是﹣3或4.
故答案为:﹣3或4.
19.解:如图所示:
.
20.解:,,,
数轴表示如下所示:
∴.
21.(1)解:由甲的描述可得,点所表示的数为,点所表示的数为5,
由乙的描述可得,点所表示的数为,点所表示的数为1,
由丙的描述可得,点所表示的数为0,
故答案为:,5,,1,0;
(2)解:在数轴上表示如图所示:
22.解:,
在数轴上表示各数如下:
用“<”号把它们连接如下:
23.
解:(1)根据题意得:小兵家的位置对应的数为2,小颖家的位置对应的数为3.5,学校的位置对应的数为-1,如图所示:
(2).
答:小兵家与学校之间的距离是3km.
(3),,.
答:小强跑步一共用了36min.
24.(1)数轴上表示2和5两点之间的距离是:,数轴上表示和的两点之间的距离是:;
故答案为:3,4.
(2),
∴,
∴,
故答案为:8或.
(3)x和的两点之间的距离为,
故答案为:.
(4)∵时,
∴,
当时,;
当时,;
故当时,代数式有最小值,且为4,
故当x取整数中的一个时,代数式有最小值为4,
故答案为:0,4.
(5)∵时,
∴,不成立;
当时,;
故,
解得,符合题意;
当时,;
故
解得,符合题意;
综上,或.
同课章节目录
