人教版七年级数学下册 期末综合检测卷 (含解析)
文档属性
| 名称 | 人教版七年级数学下册 期末综合检测卷 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 485.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-11 14:52:43 | ||
图片预览




文档简介
期末综合检测卷
一、单选题(本题共10个小题,每小题3分,共30分)
1.在实数﹣,,0.333……,,,,0.1010010001……中,无理数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,在数轴上的点 A、点 B 之间表示整数的点有( )
A.2 个 B.3 个 C.4 个 D.5 个
3.已知是二元一次方程5x+3y=1的一组解,则m的值是( )
A. B.3 C. D.
4.在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A. B. C. D.
5.如图,若点A表示数为.则( )
A. B. C. D.
6.不等式组的解集是( )
A. B. C. D.
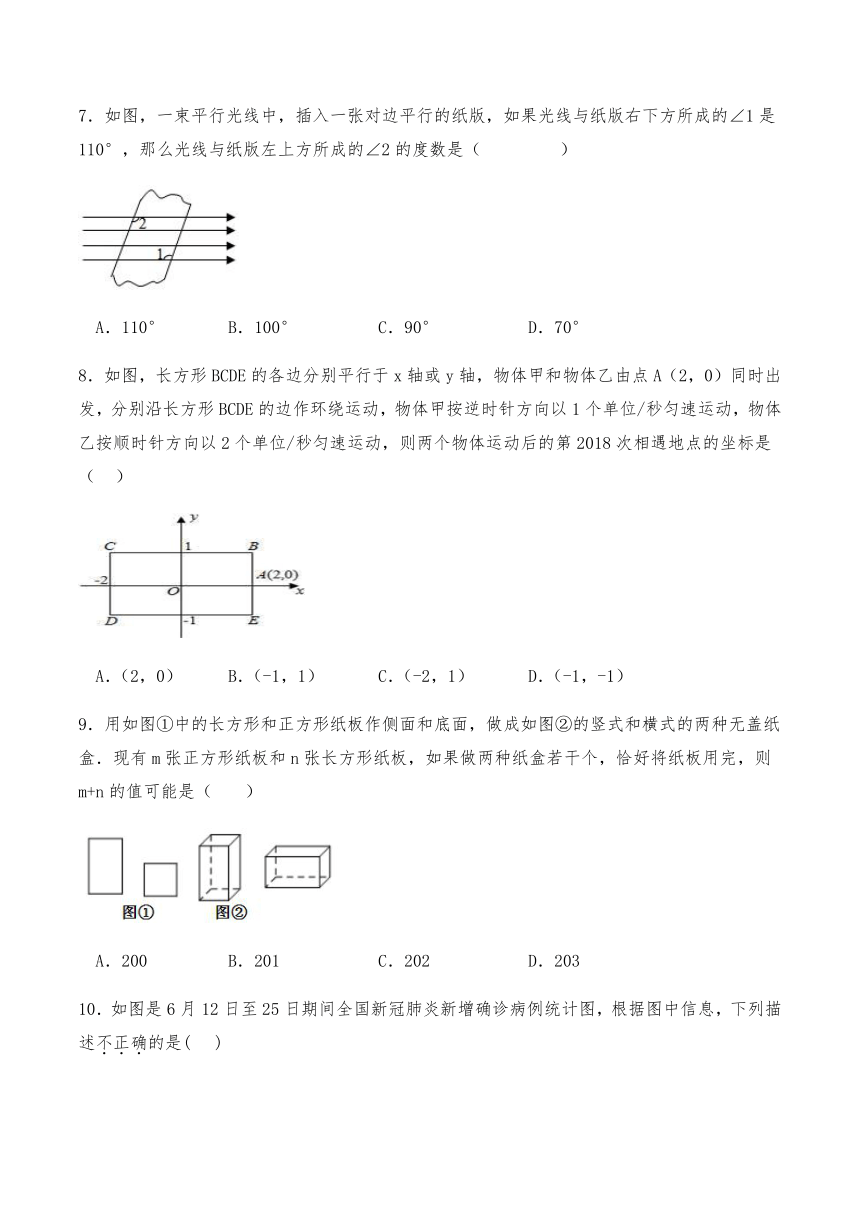
7.如图,一束平行光线中,插入一张对边平行的纸版,如果光线与纸版右下方所成的∠1是110°,那么光线与纸版左上方所成的∠2的度数是( )
A.110° B.100° C.90° D.70°
8.如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,分别沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
9.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.200 B.201 C.202 D.203
10.如图是6月12日至25日期间全国新冠肺炎新增确诊病例统计图,根据图中信息,下列描述不正确的是( )
A.13日新增确诊病例数最多 B.21日新增确诊病例数与24日相同
C.新增确诊病例数最少出现在12日 D.13日后新增确诊病例数持续下降
二、填空题(本题共8个小题,每题3分,共24分)
11.已知a,b 是有理数,且满足,那么a=________,b =________.
12.的算术平方根为__________;的倒数是__________;__________.
13.已知实数a,b在数轴上的位置如图所示,则化简的结果是______ .
14.已知关于x、y的方程组与有相同的解,则的值为________.
15.关于x的不等式组的解集如图所示,则m的值为________.
16.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为________.
17.如图,将6个大小、形状完全相同的小长方形放置在大长方形中,所标尺寸如图所示(单位:cm),则图中含有阴影部分的总面积为 _____cm2.
18.某中学随机抽查了50名学生,了解他们平均每天的睡眠时间,结果如下表所示:
时间(小时) 6 7 8 9
人数 3 6 32 9
根据学生睡眠管理相关规定﹐初中学生平均每天睡眠时间不低于8小时,该校共有学生2000人,试估计该校学生睡眠时间符合要求的约有______人.
三、解答题(本题共7个小题,19-23每题5分,24小题8分,25每题13分,共46分)
19.计算:
(1) (2)
20.解方程组
(1) (2)
21.解不等式组:,并把不等式组的解集表示在数轴上.
22.如图,在边长为1个单位长度的网格中,△ABC的三个顶点均在格点上.
(1)将△ABC先向右平移5个单位,再向上平移3个单位,得到△A1B1C1,画出平移后的△A1B1C1;
(2)建立适当的平面直角坐标系,使得点A的坐标为(﹣4,1);
(3)在(2)的条件下,直接写出点C1的坐标.
23.2021年5月19日,国家航天局发布我国首次火星探测天问一号任务探测器着陆过程两器分离和着陆后火星车拍摄的影像.我县某校以此为背景开展关于火星知识的问答竞赛.为奖励在竞赛中表现优异的学生,学校准备一次性购买,两种航天器模型作为奖品.已知购买1个模型和1个模型共需159元;购买3个模型和2个模型共需374元.
(1)求1个模型和1个模型的价格;
(2)根据学校实际情况,需一次性购买模型和模型共20个,但要求购买模型的数量多于12个,且不超过模型的3倍.请你给出一种费用最少的方案,并求出该方案所需的费用.
24.9月16日,2020线上智博会举行西部(重庆)科学城新闻发布会.会上透露,西部(重庆)科学城是“科 学家的家、创业者的城”,力争到2035年,全面建成具有全国影响力的科技创新中心核心区.为了解民众 对科学城相关知识的知晓程度,某公司派甲、乙两人各随机调查20名群众,填写了对科学城相关知识的调查问卷(满分为10分),得分用表示(为整数),数据分组为 A:0≤<2,B:2≤<4,C:4≤<6,D:6≤<8,E:8≤≤10).对问卷得分进行整理分析,给出了下面部分信息:
甲问卷得分的扇形统计图
乙问卷得分频数分布直方图(人数)
两组问卷得分的平均数,中位数,众数,满分率如下表:
平均数(分) 中位数(分) 众数(分) 满分率
甲公司 5.15 6 5%
乙公司 5.55 6 5%
甲公司B组占10%,E组占30%,A圆心角度数;
甲公司分数在C、D组的数据为:6,4,4,6,6,7,6,5;乙公司E组所有数据之和为58.
根据以上信息,解答下列问题:
(1)扇形统计图中= 度,信息表中的中位数= 分,众数= 分;
(2)通过以上数据分析,你认为 公司问卷调查的成绩更好,理由是 ;(写一条即可)
(3)若分数大于等于6即为合格,请估计问卷调查1600名群众中合格的人数是多少?
25.综合与探究
综合与实践课上,同学们以“一个含角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线,,且,三角形是直角三角形,,,
操作发现:
(1)如图1.,求的度数;
(2)如图2.创新小组的同学把直线向上平移,并把的位置改变,发现,请说明理由.
实践探究:
(3)填密小组在创新小组发现的结论的基础上,将图2中的图形继续变化得到图3,平分,此时发现与又存在新的数量关系,请写出与的数量关系并说明理由.
答案
一、单选题
1.B
【分析】无限不循环小数是无理数,根据无理数的定义逐一分析即可.
【详解】解:在实数﹣,,0.333……,,,,0.1010010001……中,
都是有理数,
无理数有:
故选B
2.C
【分析】先估算出-与的取值范围,再进行解答即可.
【详解】解:∵1<2<4,
∴1<<2,
∴-2<-<-1;
∵4<7<9,
∴2<<3,
∴点A和点B之间表示整数的点有-1,0,1,2共4个.
故选:C.
3.A
【分析】把代入5x+3y=1即可求出m的值.
【详解】解:把代入5x+3y=1,得
10+3m=1,
∴m=-3,
故选A.
4.C
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数以及点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵第二象限的点P到x轴的距离是2,到y轴的距离是3,
∴点P的横坐标是-3,纵坐标是2,
∴点P的坐标为(-3,2).
故选:C.
5.D
【分析】根据点A在数轴上的位置可得出关于x的一元一次不等式组,解之即可求解.
【详解】解:由数轴可知,1<x+1<2,
∴0<x<1,
故选:D.
6.B
【分析】利用解一元一次不等式组的一般步骤求解即可.
【详解】解:
解不等式①得:,
解不等式②得: ,
故不等式组的解集为.
故选:B.
7.A
【分析】根据AB∥CD,BC∥AD,分别得到∠1+∠ADC=180°,∠2+∠ADC=180°,因此∠1=∠2,即可求解.
【详解】解:如图:
∵AB∥CD,
∴∠1+∠ADC=180°,
∵BC∥AD,
∴∠2+∠ADC=180°,
∴∠1=∠2.
∵∠1=110°,
∴∠2=110°.
故选:A.
8.D
【分析】利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙的运动速度是物体甲的2倍,求得每一次相遇的地点,找出规律即可解答.
【详解】解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4,物体乙行的路程为12×=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇;
此时甲乙回到原出发点,则每相遇三次,甲乙两物体回到出发点,
∵,
故两个物体运动后的第2018次相遇地点是第二次相遇地点,即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇,此时相遇点的坐标为(-1,-1)
故选:D.
9.A
【分析】分别设做了竖式无盖纸盒x个,横式无盖纸盒y个,列二元一次方程组,把两个方程的两边分别相加得,易知的值一定是5的倍数,本题即解答.
【详解】解:设做成竖式无盖纸盒x个,横式无盖纸盒y个,根据题意列方程组得:
,
则两式相加得
,
∵x、y 都是正整数
∴一定是5的倍数;
∵200、201、202、203四个数中,只有200是5的倍数,
∴的值可能是200.
故选A.
10.D
【分析】直接利用折线统计图进行分别分析,即可得出答案.
【详解】解:A、∵13日新增确诊病例数最多,
∴选项A不符合题意;
B、∵21日新增确诊病例数与24日相同,
∴选项B不符合题意;
C、∵新增确诊病例数最少出现在12日,
∴选项C不符合题意;
D、由折线图知,13日后新增确诊病例数并不是持续下降,
∴选项D错误,符合题意;
故选:D.
二、填空题
11. -2 -1
【分析】利用平方与算术平方根的非负性即可解决.
【详解】解:∵,,且
∴,
∴,
故答案为:-2,-1
12. 2
【分析】根据算术平方根,倒数和绝对值的意义求解即可.
【详解】解:∵,4的算术平方根为2,
∴的算术平方根为2;
的倒数是;
,
,
故答案为:2;;.
13.b
【分析】根据图示,可得:,据此求出的结果是多少即可.
【详解】解:,
.
故答案为:.
14.3
【分析】由题意可知方程组与有相同的解,由可得x+y=3,再由可得a(x+y)+b(x+y)=9,即可求a+b的值.
【详解】解:∵方程组与有相同的解,
∴方程组与的解相同,
中①+②得,
中,③+④ 得a(x+y)+b(x+y)=9,
将代入,得,
∴,
故答案为:3.
15.2
【分析】先根据数轴写出解集,再解不等式组,即可得出结果
【详解】解:
解得:
由题意可知:x≤1
∴m-1=1
m=2
故答案为:2
16.18°
【分析】根据平角及已知条件可得,由平行线的性质可得,结合图形求解即可得.
【详解】解:∵,,
∴,
∵四边形AEGH为矩形,
∴,
∴,
∵,
∴,
故答案为:.
17.44
【分析】设小长方形的长为xcm,宽为ycm,根据长方形的对边相等,列出二元一次方程组,解之得出x,y的值,再利用阴影部分的面积=大长方形的面积﹣6×小长方形的面积,即可得出答案.
【详解】解:设小长方形的长为xcm,宽为ycm,
依题意得:,
解得:,
∴图中阴影部分的总面积=14×(6+2y)﹣6xy
=14×(6+2×2)﹣6×8×2=44(cm2).
故答案为:44.
18.1640
【分析】用总人数乘以样本中睡眠时间符合要求的人数所占比例即可.
【详解】解:人
故答案为:1640.
三、解答题
19.(1)解:原式=,
;
(2)解:原式,
=6.
20.解:(1)
①得:,
③+②得:,
解得:x=2.
将x=2代入①中,
解得:y=-1.
∴方程组的解为:.
(2),
去括号整理得:,
①得:③,
②得:④,
④-③得:15y=15,y=1.
将y=1代入①得:x=2.
∴方程组的解为:.
21.解:
,
由①得;
由②得;
数轴表示为:
所以,原不等式组的解集是.
22.(1)解:如图,△A1B1C1即为所求;
(2)
解:平面直角坐标系如图所示;
(3)解:由图象得:点C1的坐标(3,2).
23.解:(1)设1个A模型的价格为x元,1个B模型的价格为y元,
依题意得:,
解得:.
答:1个A模型的价格为56元,1个B模型的价格为103元.
(2)设购买A模型m个,则购买B模型(20-m)个,
依题意得:,
解得:12<m≤15.
又∵m为整数,
∴m可以为13,14,15,
∴共有3种购买方案,
方案1:购买A模型13个,B模型7个,所需费用为56×13+103×7=728+721=1449(元);
方案2:购买A模型14个,B模型6个,所需费用为56×14+103×6=784+618=1402(元);
方案3:购买A模型15个,B模型5个,所需费用为56×15+103×5=840+515=1355(元).
∵1449>1402>1355,
∴方案3购买A模型15个,B模型5个费用最少,最少费用为1355元.
24.解:(1)扇形图中:B组: ,E组:;
又∵甲公司分数在C、D组的数据为:6,4,4,6,6,7,6,5;共8人,
故A组为:20-2-6-8=4(人),
则 ;
∵A,B两组有6人,总共20人,故中位数在C组故n=6,
又频数直方图中数据最多的为E组:205%=1,故1人满分,
另外六人分数总分为58-10=48分,
则该6人均分为8分,
又∵该组最低分为8分,故众数也是8
故答案为:72°,6,8;
(2)根据表格可知乙公司较好,乙公司众数较甲公司的大,即成绩比较优秀;
(3)甲公司:
∵甲公司分数在C、D组的数据为:6,4,4,6,6,7,6,5,大于等于6的共5人,
E组占30%为:,
∴问卷调查1600名群众中合格的人数是: ,
乙公司:
∵中位数是6,故大于等于6的为D,E两组,
∴问卷调查1600名群众中合格的人数是:,
答:甲公司问卷调查1600名群众中合格的人数是人;乙公司问卷调查1600名群众中合格的人数是800人;.
25.解:(1)如图1 ,,
,
,
;
图1
(2)理由如下:如图2. 过点作,
图2
,
,
,
,
,
,
;
(3),
图3
理由如下:如图3,过点作,
平分,
,
,
又,
,
,
,
,
又 ,
,
.
一、单选题(本题共10个小题,每小题3分,共30分)
1.在实数﹣,,0.333……,,,,0.1010010001……中,无理数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,在数轴上的点 A、点 B 之间表示整数的点有( )
A.2 个 B.3 个 C.4 个 D.5 个
3.已知是二元一次方程5x+3y=1的一组解,则m的值是( )
A. B.3 C. D.
4.在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A. B. C. D.
5.如图,若点A表示数为.则( )
A. B. C. D.
6.不等式组的解集是( )
A. B. C. D.
7.如图,一束平行光线中,插入一张对边平行的纸版,如果光线与纸版右下方所成的∠1是110°,那么光线与纸版左上方所成的∠2的度数是( )
A.110° B.100° C.90° D.70°
8.如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,分别沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
9.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.200 B.201 C.202 D.203
10.如图是6月12日至25日期间全国新冠肺炎新增确诊病例统计图,根据图中信息,下列描述不正确的是( )
A.13日新增确诊病例数最多 B.21日新增确诊病例数与24日相同
C.新增确诊病例数最少出现在12日 D.13日后新增确诊病例数持续下降
二、填空题(本题共8个小题,每题3分,共24分)
11.已知a,b 是有理数,且满足,那么a=________,b =________.
12.的算术平方根为__________;的倒数是__________;__________.
13.已知实数a,b在数轴上的位置如图所示,则化简的结果是______ .
14.已知关于x、y的方程组与有相同的解,则的值为________.
15.关于x的不等式组的解集如图所示,则m的值为________.
16.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为________.
17.如图,将6个大小、形状完全相同的小长方形放置在大长方形中,所标尺寸如图所示(单位:cm),则图中含有阴影部分的总面积为 _____cm2.
18.某中学随机抽查了50名学生,了解他们平均每天的睡眠时间,结果如下表所示:
时间(小时) 6 7 8 9
人数 3 6 32 9
根据学生睡眠管理相关规定﹐初中学生平均每天睡眠时间不低于8小时,该校共有学生2000人,试估计该校学生睡眠时间符合要求的约有______人.
三、解答题(本题共7个小题,19-23每题5分,24小题8分,25每题13分,共46分)
19.计算:
(1) (2)
20.解方程组
(1) (2)
21.解不等式组:,并把不等式组的解集表示在数轴上.
22.如图,在边长为1个单位长度的网格中,△ABC的三个顶点均在格点上.
(1)将△ABC先向右平移5个单位,再向上平移3个单位,得到△A1B1C1,画出平移后的△A1B1C1;
(2)建立适当的平面直角坐标系,使得点A的坐标为(﹣4,1);
(3)在(2)的条件下,直接写出点C1的坐标.
23.2021年5月19日,国家航天局发布我国首次火星探测天问一号任务探测器着陆过程两器分离和着陆后火星车拍摄的影像.我县某校以此为背景开展关于火星知识的问答竞赛.为奖励在竞赛中表现优异的学生,学校准备一次性购买,两种航天器模型作为奖品.已知购买1个模型和1个模型共需159元;购买3个模型和2个模型共需374元.
(1)求1个模型和1个模型的价格;
(2)根据学校实际情况,需一次性购买模型和模型共20个,但要求购买模型的数量多于12个,且不超过模型的3倍.请你给出一种费用最少的方案,并求出该方案所需的费用.
24.9月16日,2020线上智博会举行西部(重庆)科学城新闻发布会.会上透露,西部(重庆)科学城是“科 学家的家、创业者的城”,力争到2035年,全面建成具有全国影响力的科技创新中心核心区.为了解民众 对科学城相关知识的知晓程度,某公司派甲、乙两人各随机调查20名群众,填写了对科学城相关知识的调查问卷(满分为10分),得分用表示(为整数),数据分组为 A:0≤<2,B:2≤<4,C:4≤<6,D:6≤<8,E:8≤≤10).对问卷得分进行整理分析,给出了下面部分信息:
甲问卷得分的扇形统计图
乙问卷得分频数分布直方图(人数)
两组问卷得分的平均数,中位数,众数,满分率如下表:
平均数(分) 中位数(分) 众数(分) 满分率
甲公司 5.15 6 5%
乙公司 5.55 6 5%
甲公司B组占10%,E组占30%,A圆心角度数;
甲公司分数在C、D组的数据为:6,4,4,6,6,7,6,5;乙公司E组所有数据之和为58.
根据以上信息,解答下列问题:
(1)扇形统计图中= 度,信息表中的中位数= 分,众数= 分;
(2)通过以上数据分析,你认为 公司问卷调查的成绩更好,理由是 ;(写一条即可)
(3)若分数大于等于6即为合格,请估计问卷调查1600名群众中合格的人数是多少?
25.综合与探究
综合与实践课上,同学们以“一个含角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线,,且,三角形是直角三角形,,,
操作发现:
(1)如图1.,求的度数;
(2)如图2.创新小组的同学把直线向上平移,并把的位置改变,发现,请说明理由.
实践探究:
(3)填密小组在创新小组发现的结论的基础上,将图2中的图形继续变化得到图3,平分,此时发现与又存在新的数量关系,请写出与的数量关系并说明理由.
答案
一、单选题
1.B
【分析】无限不循环小数是无理数,根据无理数的定义逐一分析即可.
【详解】解:在实数﹣,,0.333……,,,,0.1010010001……中,
都是有理数,
无理数有:
故选B
2.C
【分析】先估算出-与的取值范围,再进行解答即可.
【详解】解:∵1<2<4,
∴1<<2,
∴-2<-<-1;
∵4<7<9,
∴2<<3,
∴点A和点B之间表示整数的点有-1,0,1,2共4个.
故选:C.
3.A
【分析】把代入5x+3y=1即可求出m的值.
【详解】解:把代入5x+3y=1,得
10+3m=1,
∴m=-3,
故选A.
4.C
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数以及点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵第二象限的点P到x轴的距离是2,到y轴的距离是3,
∴点P的横坐标是-3,纵坐标是2,
∴点P的坐标为(-3,2).
故选:C.
5.D
【分析】根据点A在数轴上的位置可得出关于x的一元一次不等式组,解之即可求解.
【详解】解:由数轴可知,1<x+1<2,
∴0<x<1,
故选:D.
6.B
【分析】利用解一元一次不等式组的一般步骤求解即可.
【详解】解:
解不等式①得:,
解不等式②得: ,
故不等式组的解集为.
故选:B.
7.A
【分析】根据AB∥CD,BC∥AD,分别得到∠1+∠ADC=180°,∠2+∠ADC=180°,因此∠1=∠2,即可求解.
【详解】解:如图:
∵AB∥CD,
∴∠1+∠ADC=180°,
∵BC∥AD,
∴∠2+∠ADC=180°,
∴∠1=∠2.
∵∠1=110°,
∴∠2=110°.
故选:A.
8.D
【分析】利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙的运动速度是物体甲的2倍,求得每一次相遇的地点,找出规律即可解答.
【详解】解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4,物体乙行的路程为12×=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇;
此时甲乙回到原出发点,则每相遇三次,甲乙两物体回到出发点,
∵,
故两个物体运动后的第2018次相遇地点是第二次相遇地点,即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇,此时相遇点的坐标为(-1,-1)
故选:D.
9.A
【分析】分别设做了竖式无盖纸盒x个,横式无盖纸盒y个,列二元一次方程组,把两个方程的两边分别相加得,易知的值一定是5的倍数,本题即解答.
【详解】解:设做成竖式无盖纸盒x个,横式无盖纸盒y个,根据题意列方程组得:
,
则两式相加得
,
∵x、y 都是正整数
∴一定是5的倍数;
∵200、201、202、203四个数中,只有200是5的倍数,
∴的值可能是200.
故选A.
10.D
【分析】直接利用折线统计图进行分别分析,即可得出答案.
【详解】解:A、∵13日新增确诊病例数最多,
∴选项A不符合题意;
B、∵21日新增确诊病例数与24日相同,
∴选项B不符合题意;
C、∵新增确诊病例数最少出现在12日,
∴选项C不符合题意;
D、由折线图知,13日后新增确诊病例数并不是持续下降,
∴选项D错误,符合题意;
故选:D.
二、填空题
11. -2 -1
【分析】利用平方与算术平方根的非负性即可解决.
【详解】解:∵,,且
∴,
∴,
故答案为:-2,-1
12. 2
【分析】根据算术平方根,倒数和绝对值的意义求解即可.
【详解】解:∵,4的算术平方根为2,
∴的算术平方根为2;
的倒数是;
,
,
故答案为:2;;.
13.b
【分析】根据图示,可得:,据此求出的结果是多少即可.
【详解】解:,
.
故答案为:.
14.3
【分析】由题意可知方程组与有相同的解,由可得x+y=3,再由可得a(x+y)+b(x+y)=9,即可求a+b的值.
【详解】解:∵方程组与有相同的解,
∴方程组与的解相同,
中①+②得,
中,③+④ 得a(x+y)+b(x+y)=9,
将代入,得,
∴,
故答案为:3.
15.2
【分析】先根据数轴写出解集,再解不等式组,即可得出结果
【详解】解:
解得:
由题意可知:x≤1
∴m-1=1
m=2
故答案为:2
16.18°
【分析】根据平角及已知条件可得,由平行线的性质可得,结合图形求解即可得.
【详解】解:∵,,
∴,
∵四边形AEGH为矩形,
∴,
∴,
∵,
∴,
故答案为:.
17.44
【分析】设小长方形的长为xcm,宽为ycm,根据长方形的对边相等,列出二元一次方程组,解之得出x,y的值,再利用阴影部分的面积=大长方形的面积﹣6×小长方形的面积,即可得出答案.
【详解】解:设小长方形的长为xcm,宽为ycm,
依题意得:,
解得:,
∴图中阴影部分的总面积=14×(6+2y)﹣6xy
=14×(6+2×2)﹣6×8×2=44(cm2).
故答案为:44.
18.1640
【分析】用总人数乘以样本中睡眠时间符合要求的人数所占比例即可.
【详解】解:人
故答案为:1640.
三、解答题
19.(1)解:原式=,
;
(2)解:原式,
=6.
20.解:(1)
①得:,
③+②得:,
解得:x=2.
将x=2代入①中,
解得:y=-1.
∴方程组的解为:.
(2),
去括号整理得:,
①得:③,
②得:④,
④-③得:15y=15,y=1.
将y=1代入①得:x=2.
∴方程组的解为:.
21.解:
,
由①得;
由②得;
数轴表示为:
所以,原不等式组的解集是.
22.(1)解:如图,△A1B1C1即为所求;
(2)
解:平面直角坐标系如图所示;
(3)解:由图象得:点C1的坐标(3,2).
23.解:(1)设1个A模型的价格为x元,1个B模型的价格为y元,
依题意得:,
解得:.
答:1个A模型的价格为56元,1个B模型的价格为103元.
(2)设购买A模型m个,则购买B模型(20-m)个,
依题意得:,
解得:12<m≤15.
又∵m为整数,
∴m可以为13,14,15,
∴共有3种购买方案,
方案1:购买A模型13个,B模型7个,所需费用为56×13+103×7=728+721=1449(元);
方案2:购买A模型14个,B模型6个,所需费用为56×14+103×6=784+618=1402(元);
方案3:购买A模型15个,B模型5个,所需费用为56×15+103×5=840+515=1355(元).
∵1449>1402>1355,
∴方案3购买A模型15个,B模型5个费用最少,最少费用为1355元.
24.解:(1)扇形图中:B组: ,E组:;
又∵甲公司分数在C、D组的数据为:6,4,4,6,6,7,6,5;共8人,
故A组为:20-2-6-8=4(人),
则 ;
∵A,B两组有6人,总共20人,故中位数在C组故n=6,
又频数直方图中数据最多的为E组:205%=1,故1人满分,
另外六人分数总分为58-10=48分,
则该6人均分为8分,
又∵该组最低分为8分,故众数也是8
故答案为:72°,6,8;
(2)根据表格可知乙公司较好,乙公司众数较甲公司的大,即成绩比较优秀;
(3)甲公司:
∵甲公司分数在C、D组的数据为:6,4,4,6,6,7,6,5,大于等于6的共5人,
E组占30%为:,
∴问卷调查1600名群众中合格的人数是: ,
乙公司:
∵中位数是6,故大于等于6的为D,E两组,
∴问卷调查1600名群众中合格的人数是:,
答:甲公司问卷调查1600名群众中合格的人数是人;乙公司问卷调查1600名群众中合格的人数是800人;.
25.解:(1)如图1 ,,
,
,
;
图1
(2)理由如下:如图2. 过点作,
图2
,
,
,
,
,
,
;
(3),
图3
理由如下:如图3,过点作,
平分,
,
,
又,
,
,
,
,
又 ,
,
.
同课章节目录
