人教版七年级数学下册 10.3 实际问题与二元一次方程组同步练习(含解析)
文档属性
| 名称 | 人教版七年级数学下册 10.3 实际问题与二元一次方程组同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 385.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-11 14:53:19 | ||
图片预览



文档简介
10.3 实际问题与二元一次方程组
一、单选题
1.为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组( )
A. B.
C. D.
2.图①,图②都是由8个一样的小长方形拼成的,且图②中的阴影部分(正方形)的面积为1,设每块小长方形地砖的长为xcm,宽为ycm,下列方程组正确的是( )
A. B. C. D.
3.将一副三角板按如图方式摆放,且的度数比的度数多10°,若设, ,则可得方程组为( )
A. B.
C. D.
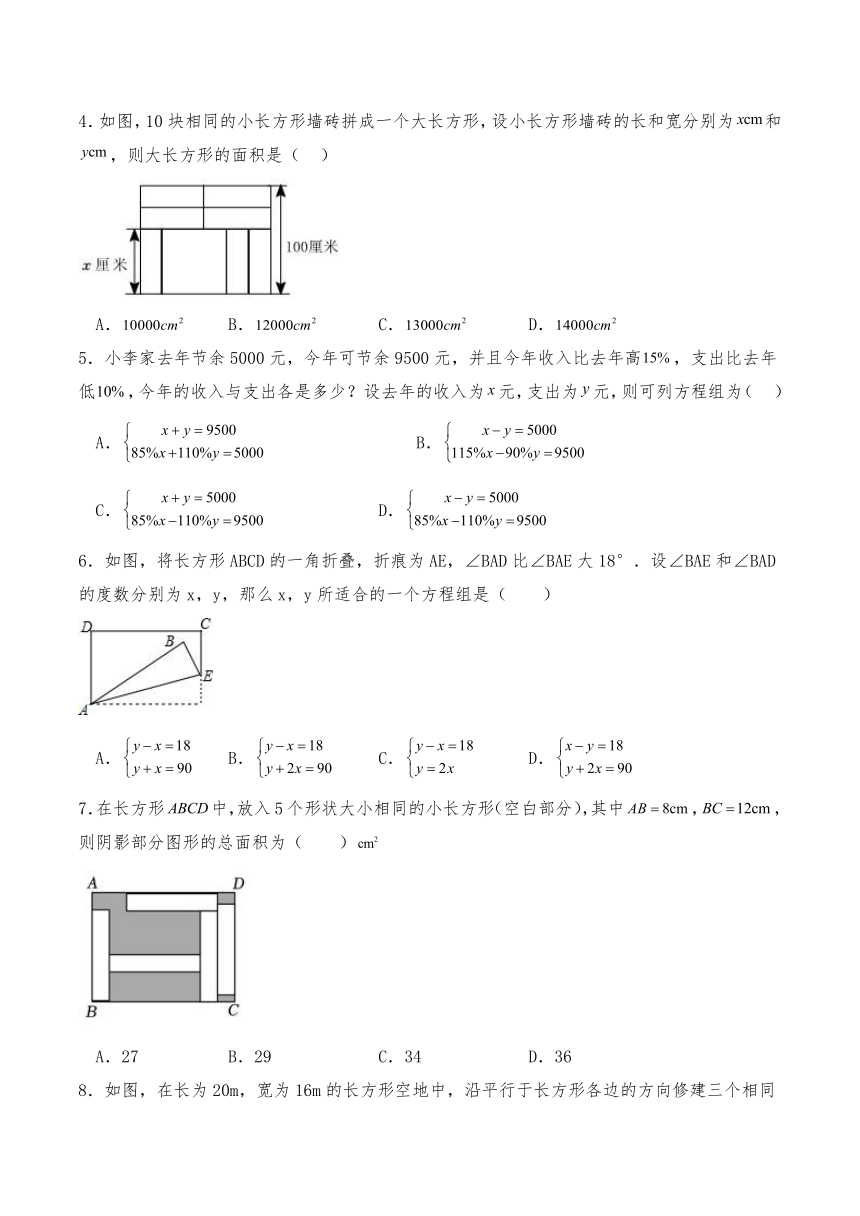
4.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为和,则大长方形的面积是( )
A. B. C. D.
5.小李家去年节余5000元,今年可节余9500元,并且今年收入比去年高,支出比去年低,今年的收入与支出各是多少?设去年的收入为元,支出为元,则可列方程组为( )
A. B.
C. D.
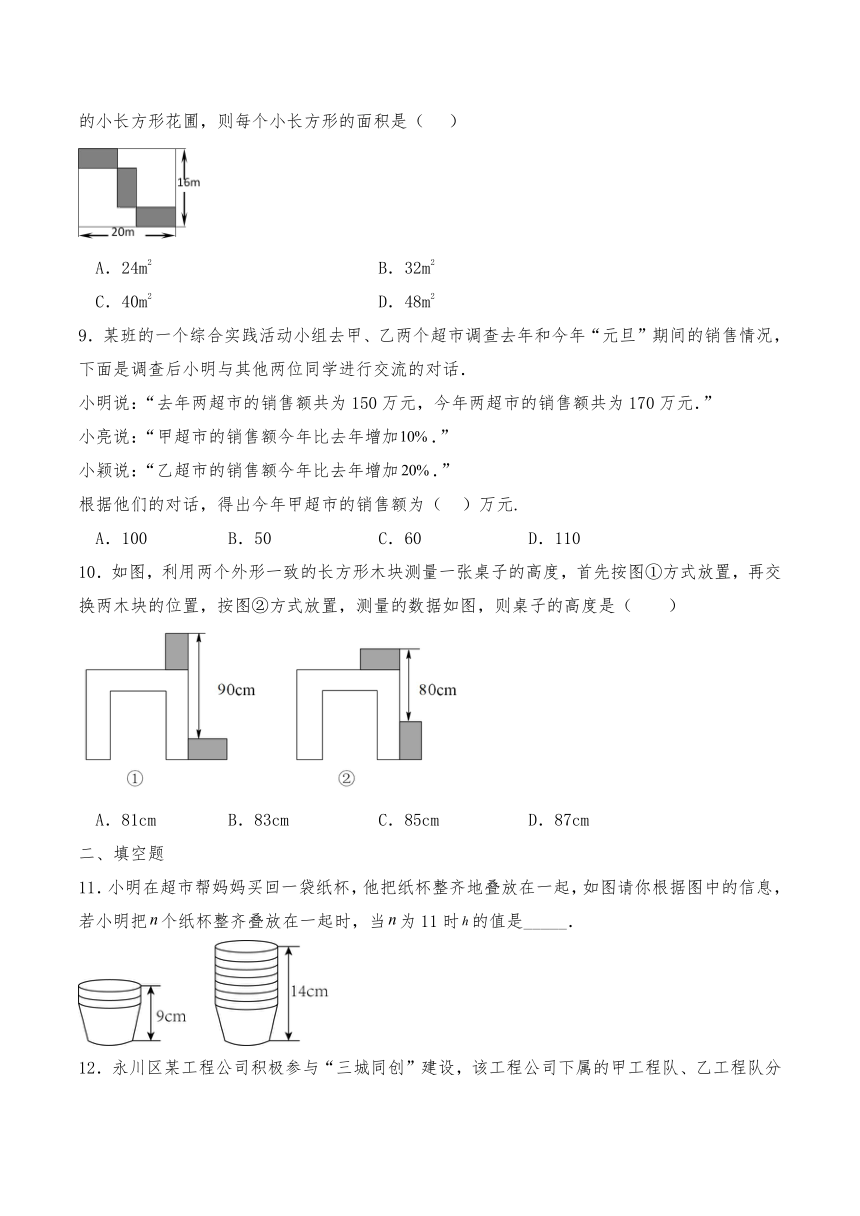
6.如图,将长方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大18°.设∠BAE和∠BAD的度数分别为x,y,那么x,y所适合的一个方程组是( )
A. B. C. D.
7.在长方形中,放入5个形状大小相同的小长方形(空白部分),其中,,则阴影部分图形的总面积为( )
A.27 B.29 C.34 D.36
8.如图,在长为20m,宽为16m的长方形空地中,沿平行于长方形各边的方向修建三个相同的小长方形花圃,则每个小长方形的面积是( )
A.24m2 B.32m2
C.40m2 D.48m2
9.某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年“元旦”期间的销售情况,下面是调查后小明与其他两位同学进行交流的对话.
小明说:“去年两超市的销售额共为150万元,今年两超市的销售额共为170万元.”
小亮说:“甲超市的销售额今年比去年增加.”
小颖说:“乙超市的销售额今年比去年增加.”
根据他们的对话,得出今年甲超市的销售额为( )万元.
A.100 B.50 C.60 D.110
10.如图,利用两个外形一致的长方形木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.81cm B.83cm C.85cm D.87cm
二、填空题
11.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把个纸杯整齐叠放在一起时,当为11时的值是_____.
12.永川区某工程公司积极参与“三城同创”建设,该工程公司下属的甲工程队、乙工程队分别承包了三城的A工程、B工程,甲工程队晴天需要14天完成,雨天工作效率下降30%;乙工程队晴天需15天完成,雨天工作效率下降20%,实际上两个工程队同时开工,同时完工,两个工程队各工作了______天.
13.某地准备对一段长1200米的河道进行消淤疏通.若甲工程队先用4天单独完成其中一部分河道的疏通任务,剩余下的任务由乙工程队单独完成需要9天;若甲工程队先单独工作8天,剩余下的任务由乙工程队单独完成需要3天.设甲工程队平均每天疏通河道x米,乙工程队每天疏通河道y米,则x+y=_____米.
14.已知两个角的两边分别平行,并且这两个角的差是20°,则这两个角分别等于_____.
15.在如图所示的长方形中放置了8个大小和形状完全相同的小长方形,设每个小长方形的长为x,宽为y,根据图中提供的数据,列方程组_______.
16.某商场购进商品后,加价40%作为销售价.五一期间,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元.则两种商品进价分别为________元.
17.如图长方形ABCD由5个部分组成,其中1、3部分是两个相同大小的正方形,2、4部分是两个相同大小的长方形,5部分是小正方形.若AB=9cm,BC=14cm,则5部分的面积为_____cm2.
18.年冬,重庆新冠疫情期间,某火锅店举办“云端火锅,共抗疫情”活动,将火锅底料及菜品打包成“便利火锅包”送至附近小区大门处,由居民自行前往提取.根据菜品种类分为A、、三类,三个品类成本价分别是元,元,元.且A类和类火锅的标价一样,该店对这三个品类全部打折销售.若三个品类的销量相同,则火锅店能获得的利润,此时A品类利润率为.若A、、三类销量之比是,则火锅店销售A、、类便利火锅包的总利润率为_______.(利润率)
三、解答题
19.通道县政府为把双江镇建设成国家级文明县城,现有一段长为180 m的街道需要整治,甲、乙两个工程队先后接力完成:甲工程队每天整治12 m,乙工程队每天整治8 m,共用时20天.问甲、乙两工程队分别整治了多少米?
20.甲乙两人同时加工一批零件,前3小时两人共加工126件,后5小时中甲先花了1小时修理工具,之后甲每小时比以前多加工10件,结果在后5小时内,甲比乙多加工了10件.甲、乙两人原来每小时各加工多少件?
21.如图,长方形ABCD中放置9个形状、大小都相同的小长方形,相关数据图中所示,则图中阴影部分的面积为多少.
22.列二元一次方程组解应用题:一个长方形的长减少,宽增加,就成为一个正方形,并且这两个图形的面积相等.这个长方形的长、宽各是多少?
23.某商店决定购进A、B两种纪念品出售,若购进A种纪念品件,B种纪念品5件,则需要元;若购进A种纪念品5件,B种纪念品件,则需要元.
(1)求A、B两种纪念品的购进单价;
(2)已知商店购进两种纪念品件,共花费元,两种纪念品均标每件元出售,其中有5件B种纪念品以七五折售出,求这件纪念品的销售利润.
24.某商场从厂家购进了两种品牌篮球共80个,已知购买品牌篮球的总价比购买品牌篮球总价的2倍还多200元,品牌篮球每个进价100元,品牌篮球每个进价80元.
(1)求购进两种品牌篮球各多少个?
(2)在销售过程中,品牌篮球每个售价150元,售出30个后出现滞销;商场决定打折出售剩余的品牌篮球,品牌篮球每个按进价加价20%销售,很快全部售出,两种品牌篮球全部售出后共获利2080元,求品牌篮球打几折出售?
答案
一、单选题
1.A
【分析】根据河道总长为180米和A、B两个工程小组共用时20天这两个等量关系列出方程,组成方程组即可求解.
【详解】解:设A工程小组整治河道x米,B工程小组整治河道y米,依题意可得:
,
故选:A.
2.A
【分析】利用长方形的对边相等及图2中的阴影部分(正方形)的面积为1(边长为1),即可得出关于x,y的二元一次方程组.
【详解】解:由图①可得:3x=5y;
由图②可得:2y x=1,
∴可得方程组
故选A.
3.B
【分析】根据等量关系:①三角板中最大的角是,从图中可看出,
②∠1比∠2的度数大 ,则.
【详解】解:由图可知: ,
又∵的度数比的度数多10°,
∴,
∵设, ,
∴联立,得到方程组: .
故选:B.
4.B
【分析】根据长方形的对边相等,可得出关于x,y的二元一次方程组,解之即可得出x,y的值,再将其代入中即可求出结论.
【详解】解∶根据题意,得,
解得,
∴,
∴大长方形的面积为.
故选:B.
5.B
【分析】根据题意可得等量关系:①去年的收入为元去年的支出元结余5000元;②今年的收入今年的支出今年可结余9500元,根据等量关系列出方程组即可.
【详解】解:设去年的收入为元,支出为元,根据题意可得:
,
故选:B.
6.B
【分析】首先根据题意可得等量关系:①∠BAD-∠BAE大18°;②∠BAD+2∠BAE=90°,根据等量关系列出方程组即可.
【详解】解:设∠BAE和∠BAD的度数分别为x°和y°,
依题意可列方程组:.
故选B.
7.D
【分析】设小长方形的长为,宽为,根据图形中大长方形的长和宽列二元一次方程组,求出x和y的值,即可解决问题.
【详解】解:设小长方形的长为,宽为,
根据题意,得:,
解得:,
∴每个小长方形的面积为,
∴阴影部分的面积,
故选:D.
8.B
【分析】由图在进行平移后可得两个小长方形的长+一个小长方形的宽=20m,两个小长方形的宽+一个小长方形的长=16m由此可设方程组进行解答.
【详解】解:设小长方形的长为xm,宽为ym,
则根据图形可得,
解得,
∴小长方形的面积为:48=32m.
故选B.
9.D
【分析】设甲超市去年销售额为x万元,乙超市去年销售额为y万元,根据题意列出方程组求解后,再求出甲超市今年的销售额即可.
【详解】解:设甲超市去年销售额为x万元,乙超市去年销售额为y万元,
根据题意,得:
,,
,
解得:,
所以今年甲超市销售额为.
故选:D.
10.C
【分析】设桌子的高度为xcm,长方体木块的长比宽长ycm,观察图①、图②,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【详解】设桌子的高度为xcm,长方体木块的长比宽长ycm,
根据题意得:,
解得:.
故选:C
二、填空题:
11.17cm
【分析】根据题意可知,单独一个纸杯的高度加三个纸杯叠放在一起高出单独一个纸杯的高度等于9,单独一个纸杯的高度加8个纸杯叠放在一起高出单独一个纸杯的高度等于14,根据这两个等量关系,可列出方程组,再求解.
【详解】解:设每两个纸杯叠放在一起比单独的一个纸杯增高,单独一个纸杯的高度为
由题意得
解得,
则个纸杯叠放在一起时的高度为:,
当时,其高度为:.
故答案为:.
12.17
【分析】设晴天工作x天,雨天工作y天,根据题意列出二元一次方程组求解即可.
【详解】解:设晴天工作x天,雨天工作y天,
根据题意得:,
解得:,
∴两个工程队各工作了x+y=17天,
故答案为17.
13.200
【分析】设甲工程队平均每天疏通河道x米,乙工程队每天疏通河道y米,根据题意可得,甲4天,乙9天完成任务,甲8天,乙3天完成任务,据此列方程组求解.
【详解】解:设甲工程队平均每天疏通河道x米,乙工程队每天疏通河道y米,
由题意得,,
解得:,则x+y=120+80=200(米).
故答案为200.
14.100°或80°
【分析】根据如果两个角的两边分别平行,那么这两个角相等或互补,即可列出方程组,解方程组即可求解.
【详解】解:设这两个角分别为x°,y°(假定x>y),由题意得:
,
解得x=100,y=80.
故这两个角是100°和80°,
故答案为:100°,80°.
15.
【分析】设小长方形的长为x,宽为y,根据长方形ABCD的长为17,宽的两种不同的表达式列出方程组即可得解;
【详解】解:设小长方形的长为x,宽为y,根据题意得:
,
整理得:;
故答案为:
16.200,200
【分析】设甲、乙两种商品的进价分别为x元、y元,然后根据“某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元”列方程组求解即可.
【详解】解:设甲、乙两种商品的进价分别为x元、y元.
由题意可得:
解得 .
故答案为200、200.
17.
【分析】设未知数,分别设1、3部分的大正方形边长为acm,5部分的小方形为bcm,由图可知,则2和4的长为(a+b)cm,宽为(a-b)cm,由AB=9cm,BC=14cm,可列出二元一次方程组,解出a、b,根据正方形的面积公式即可求出答案.
【详解】解:设1、3部分的大正方形边长为acm,5部分的小方形为bcm,则2和4的长为(a+b)cm,宽为(a-b)cm,得:
∵,,
∴
解得:,
∴5部分的面积 cm2
故答案为:.
18.
【分析】可设A、B、C三类的标价分别为x元,x元,y元,根据所给的条件可列出三元一次方程组,解方程组得出相应的x,y的值,从而可求解.
【详解】解:设A、B、C三类的标价分别为x元,x元,y元,依题意得:
,
解得:,
故B类的利润率为:,
C类的利润率为:,
当A、B、C三类销量之比是,则火锅店销售A、B、C类便利火锅包的总利润率为:
.
故答案为:.
三、解答题:
19.解:设甲、乙两工程队分别整治了米和米,
根据题意列方程得 ,
解得,
答:甲工程队整治了60米,乙工程队整治了120米.
20.解:设甲、乙两人原来每小时分别加工、件.
依题意得,
解方程得.
答:甲、乙两人原来每小时分别加工20,22件.
21.解:设小长方形的长为x,宽为y,依题意有
,
解得:,
9×(4+1×3)-5×1×9
=9×7-45
=63-45
=18.
答:图中阴影部分的面积为18.
22.解:设长方形的长、宽各是,,
由题意列方程组,得
解这个方程组,得
答:长方形的长、宽分别是、.
23.(1)设A种纪念品的购进单价为x元,B种纪念品的购进单价为y元,
根据题意,得
解得
答:A种纪念品的购进单价为15元,B种纪念品的购进单价为13元.
(2)设购进A种纪念品m件,B种纪念品n件,
依题意,得
所以
售完利润为:(元)
答:这32件纪念品的销售利润为元.
24.(1)解:设购进品牌篮球个,则购进品牌篮球个,
,
解得,
故购进品牌篮球50个,购进品牌篮球30个;
(2)解:设品牌篮球打折出售,依题意有:
,
即:,
解得:,
故品牌篮球打7折出售.
一、单选题
1.为打造三墩五里塘河河道风光带,现有一段长为180米的河道整治任务,由A、B两个工程小组先后接力完成,A工程小组每天整治12米,B工程小组每天整治8米,共用时20天,设A工程小组整治河道x米,B工程小组整治河道y米,依题意可列方程组( )
A. B.
C. D.
2.图①,图②都是由8个一样的小长方形拼成的,且图②中的阴影部分(正方形)的面积为1,设每块小长方形地砖的长为xcm,宽为ycm,下列方程组正确的是( )
A. B. C. D.
3.将一副三角板按如图方式摆放,且的度数比的度数多10°,若设, ,则可得方程组为( )
A. B.
C. D.
4.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为和,则大长方形的面积是( )
A. B. C. D.
5.小李家去年节余5000元,今年可节余9500元,并且今年收入比去年高,支出比去年低,今年的收入与支出各是多少?设去年的收入为元,支出为元,则可列方程组为( )
A. B.
C. D.
6.如图,将长方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大18°.设∠BAE和∠BAD的度数分别为x,y,那么x,y所适合的一个方程组是( )
A. B. C. D.
7.在长方形中,放入5个形状大小相同的小长方形(空白部分),其中,,则阴影部分图形的总面积为( )
A.27 B.29 C.34 D.36
8.如图,在长为20m,宽为16m的长方形空地中,沿平行于长方形各边的方向修建三个相同的小长方形花圃,则每个小长方形的面积是( )
A.24m2 B.32m2
C.40m2 D.48m2
9.某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年“元旦”期间的销售情况,下面是调查后小明与其他两位同学进行交流的对话.
小明说:“去年两超市的销售额共为150万元,今年两超市的销售额共为170万元.”
小亮说:“甲超市的销售额今年比去年增加.”
小颖说:“乙超市的销售额今年比去年增加.”
根据他们的对话,得出今年甲超市的销售额为( )万元.
A.100 B.50 C.60 D.110
10.如图,利用两个外形一致的长方形木块测量一张桌子的高度,首先按图①方式放置,再交换两木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.81cm B.83cm C.85cm D.87cm
二、填空题
11.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把个纸杯整齐叠放在一起时,当为11时的值是_____.
12.永川区某工程公司积极参与“三城同创”建设,该工程公司下属的甲工程队、乙工程队分别承包了三城的A工程、B工程,甲工程队晴天需要14天完成,雨天工作效率下降30%;乙工程队晴天需15天完成,雨天工作效率下降20%,实际上两个工程队同时开工,同时完工,两个工程队各工作了______天.
13.某地准备对一段长1200米的河道进行消淤疏通.若甲工程队先用4天单独完成其中一部分河道的疏通任务,剩余下的任务由乙工程队单独完成需要9天;若甲工程队先单独工作8天,剩余下的任务由乙工程队单独完成需要3天.设甲工程队平均每天疏通河道x米,乙工程队每天疏通河道y米,则x+y=_____米.
14.已知两个角的两边分别平行,并且这两个角的差是20°,则这两个角分别等于_____.
15.在如图所示的长方形中放置了8个大小和形状完全相同的小长方形,设每个小长方形的长为x,宽为y,根据图中提供的数据,列方程组_______.
16.某商场购进商品后,加价40%作为销售价.五一期间,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元.则两种商品进价分别为________元.
17.如图长方形ABCD由5个部分组成,其中1、3部分是两个相同大小的正方形,2、4部分是两个相同大小的长方形,5部分是小正方形.若AB=9cm,BC=14cm,则5部分的面积为_____cm2.
18.年冬,重庆新冠疫情期间,某火锅店举办“云端火锅,共抗疫情”活动,将火锅底料及菜品打包成“便利火锅包”送至附近小区大门处,由居民自行前往提取.根据菜品种类分为A、、三类,三个品类成本价分别是元,元,元.且A类和类火锅的标价一样,该店对这三个品类全部打折销售.若三个品类的销量相同,则火锅店能获得的利润,此时A品类利润率为.若A、、三类销量之比是,则火锅店销售A、、类便利火锅包的总利润率为_______.(利润率)
三、解答题
19.通道县政府为把双江镇建设成国家级文明县城,现有一段长为180 m的街道需要整治,甲、乙两个工程队先后接力完成:甲工程队每天整治12 m,乙工程队每天整治8 m,共用时20天.问甲、乙两工程队分别整治了多少米?
20.甲乙两人同时加工一批零件,前3小时两人共加工126件,后5小时中甲先花了1小时修理工具,之后甲每小时比以前多加工10件,结果在后5小时内,甲比乙多加工了10件.甲、乙两人原来每小时各加工多少件?
21.如图,长方形ABCD中放置9个形状、大小都相同的小长方形,相关数据图中所示,则图中阴影部分的面积为多少.
22.列二元一次方程组解应用题:一个长方形的长减少,宽增加,就成为一个正方形,并且这两个图形的面积相等.这个长方形的长、宽各是多少?
23.某商店决定购进A、B两种纪念品出售,若购进A种纪念品件,B种纪念品5件,则需要元;若购进A种纪念品5件,B种纪念品件,则需要元.
(1)求A、B两种纪念品的购进单价;
(2)已知商店购进两种纪念品件,共花费元,两种纪念品均标每件元出售,其中有5件B种纪念品以七五折售出,求这件纪念品的销售利润.
24.某商场从厂家购进了两种品牌篮球共80个,已知购买品牌篮球的总价比购买品牌篮球总价的2倍还多200元,品牌篮球每个进价100元,品牌篮球每个进价80元.
(1)求购进两种品牌篮球各多少个?
(2)在销售过程中,品牌篮球每个售价150元,售出30个后出现滞销;商场决定打折出售剩余的品牌篮球,品牌篮球每个按进价加价20%销售,很快全部售出,两种品牌篮球全部售出后共获利2080元,求品牌篮球打几折出售?
答案
一、单选题
1.A
【分析】根据河道总长为180米和A、B两个工程小组共用时20天这两个等量关系列出方程,组成方程组即可求解.
【详解】解:设A工程小组整治河道x米,B工程小组整治河道y米,依题意可得:
,
故选:A.
2.A
【分析】利用长方形的对边相等及图2中的阴影部分(正方形)的面积为1(边长为1),即可得出关于x,y的二元一次方程组.
【详解】解:由图①可得:3x=5y;
由图②可得:2y x=1,
∴可得方程组
故选A.
3.B
【分析】根据等量关系:①三角板中最大的角是,从图中可看出,
②∠1比∠2的度数大 ,则.
【详解】解:由图可知: ,
又∵的度数比的度数多10°,
∴,
∵设, ,
∴联立,得到方程组: .
故选:B.
4.B
【分析】根据长方形的对边相等,可得出关于x,y的二元一次方程组,解之即可得出x,y的值,再将其代入中即可求出结论.
【详解】解∶根据题意,得,
解得,
∴,
∴大长方形的面积为.
故选:B.
5.B
【分析】根据题意可得等量关系:①去年的收入为元去年的支出元结余5000元;②今年的收入今年的支出今年可结余9500元,根据等量关系列出方程组即可.
【详解】解:设去年的收入为元,支出为元,根据题意可得:
,
故选:B.
6.B
【分析】首先根据题意可得等量关系:①∠BAD-∠BAE大18°;②∠BAD+2∠BAE=90°,根据等量关系列出方程组即可.
【详解】解:设∠BAE和∠BAD的度数分别为x°和y°,
依题意可列方程组:.
故选B.
7.D
【分析】设小长方形的长为,宽为,根据图形中大长方形的长和宽列二元一次方程组,求出x和y的值,即可解决问题.
【详解】解:设小长方形的长为,宽为,
根据题意,得:,
解得:,
∴每个小长方形的面积为,
∴阴影部分的面积,
故选:D.
8.B
【分析】由图在进行平移后可得两个小长方形的长+一个小长方形的宽=20m,两个小长方形的宽+一个小长方形的长=16m由此可设方程组进行解答.
【详解】解:设小长方形的长为xm,宽为ym,
则根据图形可得,
解得,
∴小长方形的面积为:48=32m.
故选B.
9.D
【分析】设甲超市去年销售额为x万元,乙超市去年销售额为y万元,根据题意列出方程组求解后,再求出甲超市今年的销售额即可.
【详解】解:设甲超市去年销售额为x万元,乙超市去年销售额为y万元,
根据题意,得:
,,
,
解得:,
所以今年甲超市销售额为.
故选:D.
10.C
【分析】设桌子的高度为xcm,长方体木块的长比宽长ycm,观察图①、图②,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【详解】设桌子的高度为xcm,长方体木块的长比宽长ycm,
根据题意得:,
解得:.
故选:C
二、填空题:
11.17cm
【分析】根据题意可知,单独一个纸杯的高度加三个纸杯叠放在一起高出单独一个纸杯的高度等于9,单独一个纸杯的高度加8个纸杯叠放在一起高出单独一个纸杯的高度等于14,根据这两个等量关系,可列出方程组,再求解.
【详解】解:设每两个纸杯叠放在一起比单独的一个纸杯增高,单独一个纸杯的高度为
由题意得
解得,
则个纸杯叠放在一起时的高度为:,
当时,其高度为:.
故答案为:.
12.17
【分析】设晴天工作x天,雨天工作y天,根据题意列出二元一次方程组求解即可.
【详解】解:设晴天工作x天,雨天工作y天,
根据题意得:,
解得:,
∴两个工程队各工作了x+y=17天,
故答案为17.
13.200
【分析】设甲工程队平均每天疏通河道x米,乙工程队每天疏通河道y米,根据题意可得,甲4天,乙9天完成任务,甲8天,乙3天完成任务,据此列方程组求解.
【详解】解:设甲工程队平均每天疏通河道x米,乙工程队每天疏通河道y米,
由题意得,,
解得:,则x+y=120+80=200(米).
故答案为200.
14.100°或80°
【分析】根据如果两个角的两边分别平行,那么这两个角相等或互补,即可列出方程组,解方程组即可求解.
【详解】解:设这两个角分别为x°,y°(假定x>y),由题意得:
,
解得x=100,y=80.
故这两个角是100°和80°,
故答案为:100°,80°.
15.
【分析】设小长方形的长为x,宽为y,根据长方形ABCD的长为17,宽的两种不同的表达式列出方程组即可得解;
【详解】解:设小长方形的长为x,宽为y,根据题意得:
,
整理得:;
故答案为:
16.200,200
【分析】设甲、乙两种商品的进价分别为x元、y元,然后根据“某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元”列方程组求解即可.
【详解】解:设甲、乙两种商品的进价分别为x元、y元.
由题意可得:
解得 .
故答案为200、200.
17.
【分析】设未知数,分别设1、3部分的大正方形边长为acm,5部分的小方形为bcm,由图可知,则2和4的长为(a+b)cm,宽为(a-b)cm,由AB=9cm,BC=14cm,可列出二元一次方程组,解出a、b,根据正方形的面积公式即可求出答案.
【详解】解:设1、3部分的大正方形边长为acm,5部分的小方形为bcm,则2和4的长为(a+b)cm,宽为(a-b)cm,得:
∵,,
∴
解得:,
∴5部分的面积 cm2
故答案为:.
18.
【分析】可设A、B、C三类的标价分别为x元,x元,y元,根据所给的条件可列出三元一次方程组,解方程组得出相应的x,y的值,从而可求解.
【详解】解:设A、B、C三类的标价分别为x元,x元,y元,依题意得:
,
解得:,
故B类的利润率为:,
C类的利润率为:,
当A、B、C三类销量之比是,则火锅店销售A、B、C类便利火锅包的总利润率为:
.
故答案为:.
三、解答题:
19.解:设甲、乙两工程队分别整治了米和米,
根据题意列方程得 ,
解得,
答:甲工程队整治了60米,乙工程队整治了120米.
20.解:设甲、乙两人原来每小时分别加工、件.
依题意得,
解方程得.
答:甲、乙两人原来每小时分别加工20,22件.
21.解:设小长方形的长为x,宽为y,依题意有
,
解得:,
9×(4+1×3)-5×1×9
=9×7-45
=63-45
=18.
答:图中阴影部分的面积为18.
22.解:设长方形的长、宽各是,,
由题意列方程组,得
解这个方程组,得
答:长方形的长、宽分别是、.
23.(1)设A种纪念品的购进单价为x元,B种纪念品的购进单价为y元,
根据题意,得
解得
答:A种纪念品的购进单价为15元,B种纪念品的购进单价为13元.
(2)设购进A种纪念品m件,B种纪念品n件,
依题意,得
所以
售完利润为:(元)
答:这32件纪念品的销售利润为元.
24.(1)解:设购进品牌篮球个,则购进品牌篮球个,
,
解得,
故购进品牌篮球50个,购进品牌篮球30个;
(2)解:设品牌篮球打折出售,依题意有:
,
即:,
解得:,
故品牌篮球打7折出售.
同课章节目录
