流程图

课件15张PPT。流程图 处理事情的过程，可以按先后次序用框图来表示,这样的框图称为工序流程图(又称统筹图）复习 一公司要对某产品进行投资，那么请画出下面两方案的流程图：
方案1:先立项，然后派调研人员依次赴北京、上海、广州调研,待调研人员回来后决定生产数量；
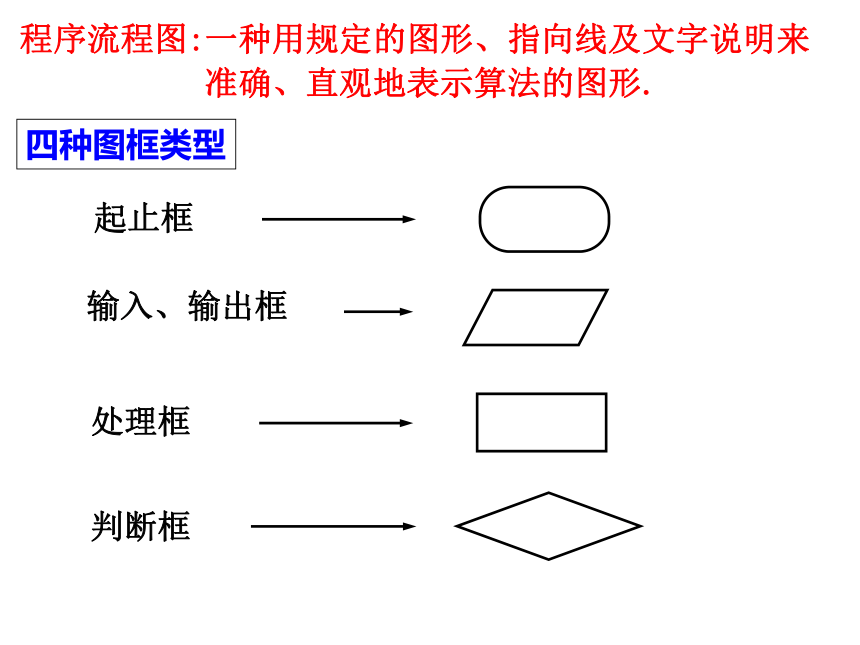
方案2:先立项，然后分别派三组调研人员赴北京、上海、广州调研,以便提前结束调研,尽早投产使产品占领市场.四种图框类型程序流程图:一种用规定的图形、指向线及文字说明来
准确、直观地表示算法的图形.例题讲解例1.试用框图描述一元二次不等式ax2+bx+c>0(a>0)的
求解过程.变.试用框图描述一元二次不等式ax2+bx+c≤0(a>0)的
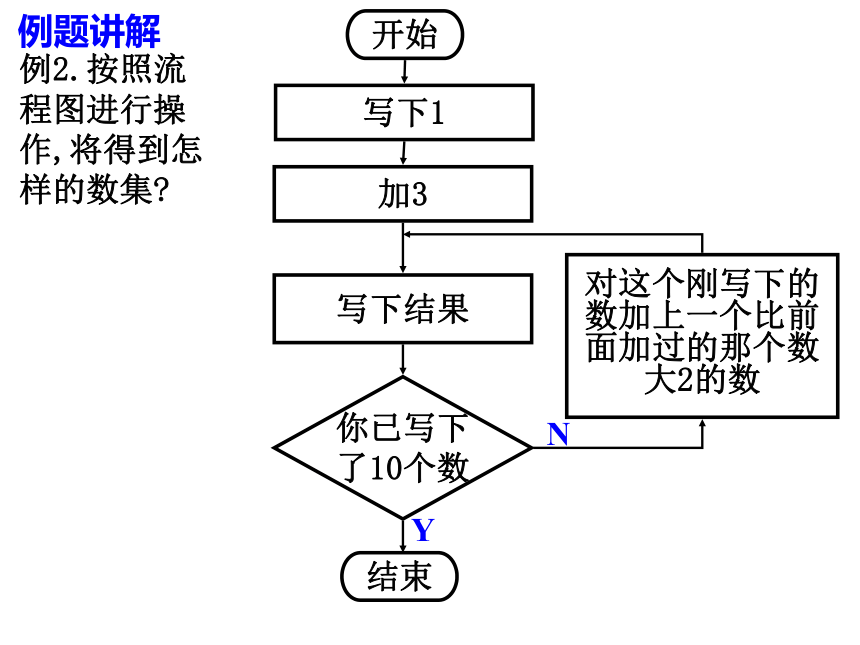
求解过程.例题讲解例2.按照流程图进行操作,将得到怎样的数集?开始写下1加3对这个刚写下的
数加上一个比前
面加过的那个数
大2的数你已写下
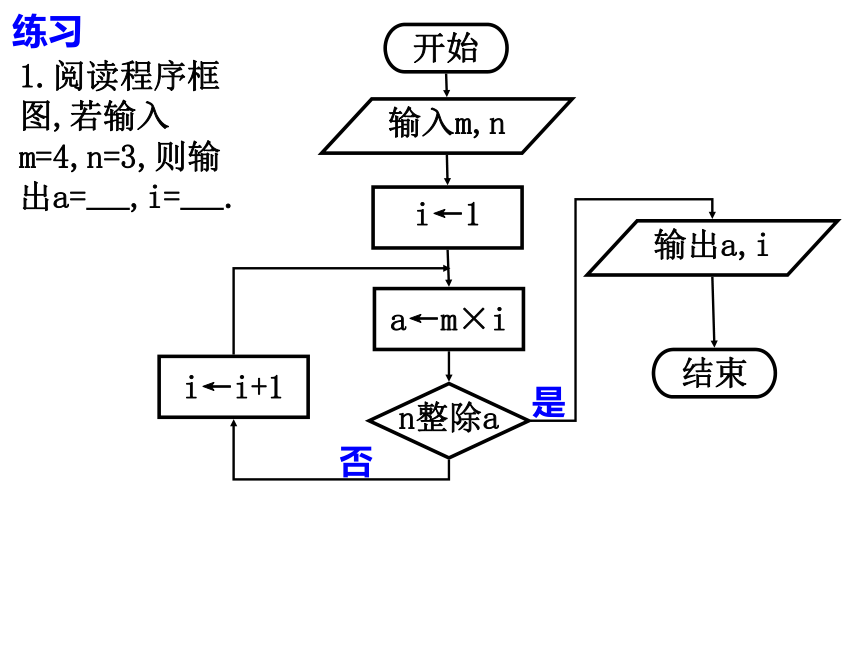
了10个数写下结果结束NY练习1.阅读程序框图,若输入m=4,n=3,则输出a=——,i=——.开始结束输入m,ni←1a←m×in整除a输出a,ii←i+1是否练习2.执行右面的程序,
若p=0.8,则输出的
n=———.开始输入pSx输出x结束x←a是x←bx←c否是否练习4.请设计输出两点连线斜率的程序框图.开始输入x1,x2,y1,y2x1=x2 y1-y2
k←———
x1-x2输出k结束是否输出斜率不存在 运用数学知识与方法解决实际问题的过程就是数学建模的过程,数学建模的过程可以用右面的流程图表示.实际背景提出问题数学模型数学结果检验可用结果不符合实际符合实际修改以“哥尼斯堡七桥问题”为例来体会数学建模的过程.1.实际情景
在18世纪的东普鲁士,有一个叫哥尼斯堡的城市.城中有一条河,河中有两个小岛,河上架有7座桥,把小岛和两岸都连接起来.
2.提出问题
人们常在桥上走过,于是产生了一个有趣的想法:能否一次走遍7座桥,而每座桥只经过1次呢?
尽管许多人绞尽脑汁,但谁也没有找到这样的一条路线.图（1）图（2）图（3）3.建立数学模型
1736年,这件事情传到了瑞士大数学家欧拉的耳朵里,他立即对这个问题产生的兴趣,动手研究起来.作为一个数学家,他的研究方法和一般人不同,他没有去到桥上走走,而是将具体问题转化为一个数学模型.
他用点代表两岸和小岛,用线代表桥,于是那个问题就转化为右图是否能一笔画出来,使得路线不重复.图(3)4.数学结果
能一笔画网络条件是:它要么没有奇点,要么最多只有两个奇点(分别作为起点和终点),而图中所有的点均为奇点,故不能一笔画.5.回到实际问题
找不到一条路线能不重复走遍7座桥. 欧拉对“七桥问题”的研究是图论研究的开始，同时也为拓扑学的研究提供了一个初等的例子.小结：1.流程图
(1)程序流程图：一种用规定的图形、指向线及文字说明
来准确、直观地表示算法的图形.
(2)工序流程图：用于描述处理事情的先后次序的框图.
2.数学建模的过程课本P83 第6,7,8题作业实际应用 公历规定:如果年份数字被4整除而不被100整除,就是润年;如果年份数字被400整除,也是润年;其它的年份都不是闰年.将这个规定用程序框图表示,并验证1980年和2000年是否是闰年.开始输入年份4是否能
整除年份100是否能
整除年份400是否能
整除年份输出“是润年”输出“不是润年”结束否是是是否否