抛物线的简单几何性质(1)
图片预览




文档简介
(共19张PPT)
抛物线的简单几何性质(1)
怀化铁路第一中学 向重新
一、温故知新
(一) 圆锥曲线的统一定义
平面内,到定点F的距离与到定直线l的距离比为常数e的点的轨迹,
当e>1时,是双曲线 .
当0(定点F不在定直线l上)
当e=1时,是抛物线 .
(二) 抛物线的标准方程
(1)开口向右
y2 = 2px (p>0)
(2)开口向左
y2 = -2px (p>0)
(3)开口向上
x2 = 2py (p>0)
(4)开口向下
x2 = -2py (p>0)
范围
1、
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
二、探索新知
如何研究抛物线y2 =2px(p>0)的几何性质
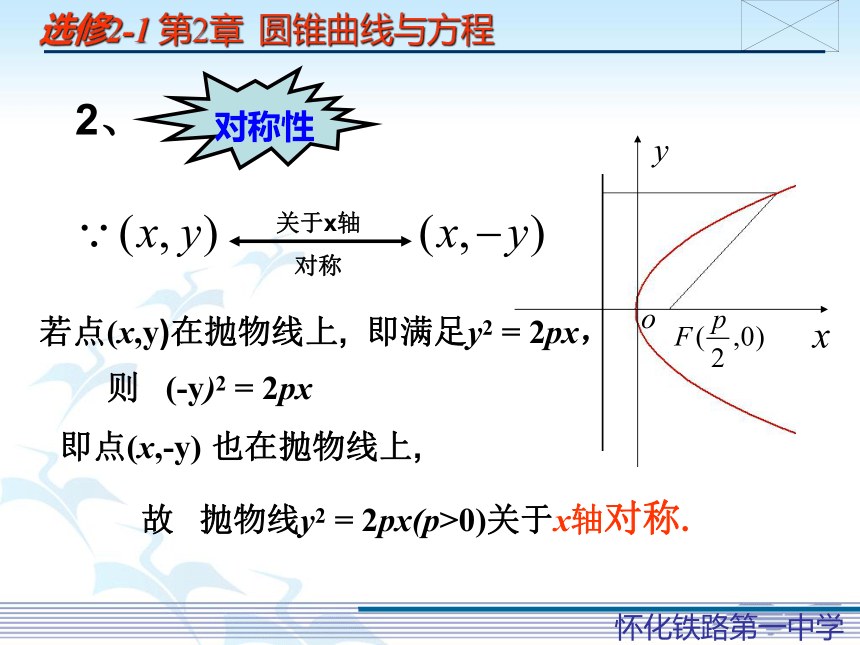
对称性
2、
关于x轴
对称
即点(x,-y) 也在抛物线上,
故 抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
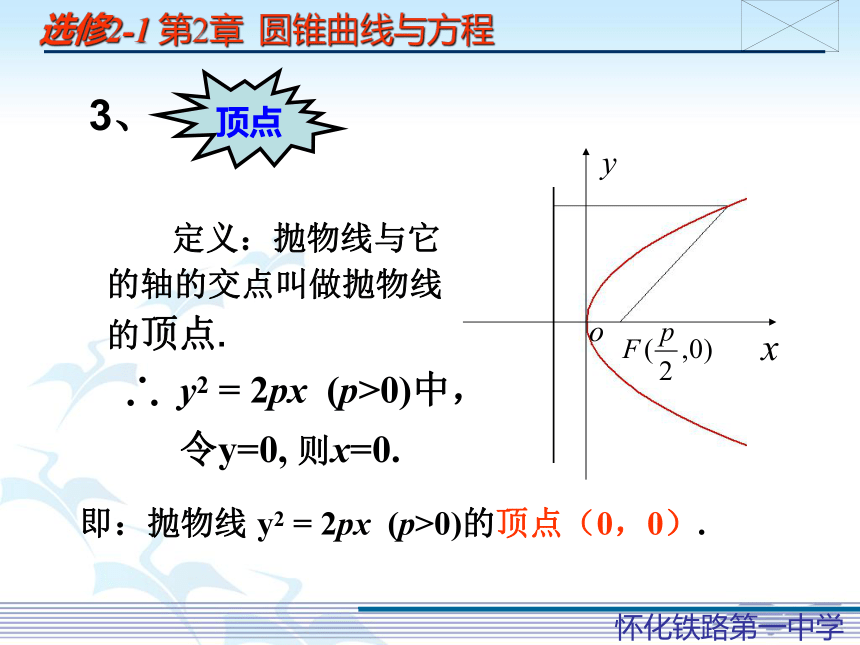
顶点
3、
定义:抛物线与它的轴的交点叫做抛物线的顶点.
y2 = 2px (p>0)中,
令y=0, 则x=0.
即:抛物线 y2 = 2px (p>0)的顶点(0,0).
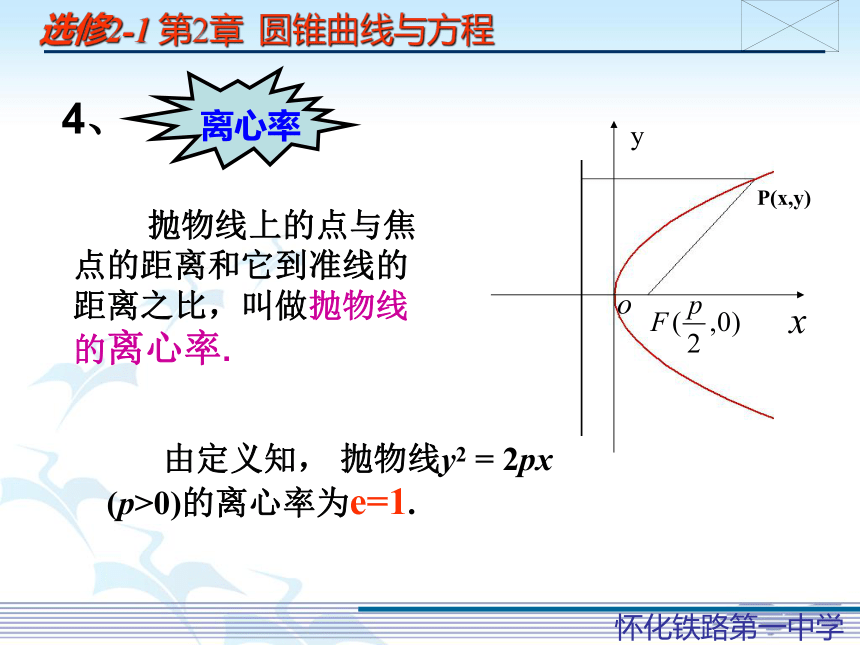
离心率
4、
P(x,y)
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.
x
y
O
F
A
B
y2=2px
2p
过焦点而垂直于对称轴的弦AB,称为抛物线的通径,
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
|AB|=2p
通径
5、
2p越大,抛物线张口越大.
方程 图形 准线 焦点 对称轴
x轴
x轴
y轴
y轴
P(x,y)
P(x,y)
P(x,y)
O
探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是抛物镜面.
抛物镜面:抛物线绕其对称轴旋转而成的曲面.
灯泡放在抛物线的焦点位置上,通过镜面反射就
变成了平行光束,这就是探照灯、汽车前灯、手电筒
的设计原理.
平行光线射到抛物镜面上,经镜面反射后,反射光
线都经过抛物线的焦点,这就是太阳灶能把光能转化为
热能的理论依据.
归纳:
(1)、抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2)、抛物线只有一条对称轴,没有对称中心;
(3)、抛物线只有一个顶点,一个焦点,一条准线;
(4)、抛物线的离心率是确定的,为1,
⑸、抛物线的通径为2P, 2p越大,抛物线的张口越大.
解法1:
例1:斜率为1的直线l 经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点,求线段AB的长.
三、典例精析
由抛物线方程
焦点F的坐标;
又k=1
直线l 的方程;
联立方程
A、B的坐标;
运用两点间的距离公式
求|AB|的值.
运算复杂
解法2:
由已知,
p=2,
焦点F(1,0),
∴直线AB的方程为
联立方程
故 |AB|=8.
O
x
y
例1:斜率为1的直线l 经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点,求线段AB的长.
准线: x=-1,
F
x=-1
A
B
设A(x1, y1)、B (x2, y2), 则
消去y得:
归纳:
O
x
y
F
M
N
(1)、抛物线的焦半径公式
(2)、抛物线的焦点弦长公式
(1)已知点A(-2,3)与抛物线y2=2px (p>0)的焦点
的距离是5,则P= .
(2)抛物线y2=4x 的弦AB垂直x轴,若|AB|= ,则
焦点到AB的距离为 .
4
2
(3)已知直线x-y=2与抛物线y2=4x 交于A、B两点,
那么线段AB的中点 坐标是 .
课堂练习
y
x
o
例2、正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px (p>0)上,求这个三角形的边长.
解:如图,设正三角形OAB的顶点A、B在抛物线上,且坐标分别为(x1,y1)、(x2,y2), 则
y12=2px1
y22=2px2
分析:
观察图形,正三角形和抛物线都是轴对称图形,
点A、B关于x轴对称,
必须加以证明!
即证A、B的横坐标相等,纵坐标互为相反数.
A
B
又|OA|=|OB|,所以x12+y12=x22+y22
y
x
o
A
B
由此可得|y1|=|y2|,
∵ x1>0,x2>0,2p>0, ∴ x1=x2
所以由
即线段AB关于x轴对称,
因为x轴垂直于AB,
(x1-x2)(x1+x2+2p)=0.
(x12-x22)+2p(x1-x2)=0,
即 :x12-x22+2px1-2px2=0,
又|OA|=|OB|,所以x12+y12=x22+y22
1、一个正三角形的三个顶点,都在抛物线
上,其中一个顶点为坐标原点,则这个三角形的
面积为 .
课堂练习
五、归纳总结
抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
抛物线只有一条对称轴,没有对称中心;
抛物线的离心率是1;
抛物线只有一个顶点;
抛物线的通径为2P,通径越大抛物线的张口越大.
1、范围:
2、对称性:
3、顶点:
4、离心率:
5、通径:
6、光学性质:
从焦点出发的光线,通过抛物线反射就变成了平行光束.
抛物线的简单几何性质(1)
怀化铁路第一中学 向重新
一、温故知新
(一) 圆锥曲线的统一定义
平面内,到定点F的距离与到定直线l的距离比为常数e的点的轨迹,
当e>1时,是双曲线 .
当0
当e=1时,是抛物线 .
(二) 抛物线的标准方程
(1)开口向右
y2 = 2px (p>0)
(2)开口向左
y2 = -2px (p>0)
(3)开口向上
x2 = 2py (p>0)
(4)开口向下
x2 = -2py (p>0)
范围
1、
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
二、探索新知
如何研究抛物线y2 =2px(p>0)的几何性质
对称性
2、
关于x轴
对称
即点(x,-y) 也在抛物线上,
故 抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
顶点
3、
定义:抛物线与它的轴的交点叫做抛物线的顶点.
y2 = 2px (p>0)中,
令y=0, 则x=0.
即:抛物线 y2 = 2px (p>0)的顶点(0,0).
离心率
4、
P(x,y)
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.
x
y
O
F
A
B
y2=2px
2p
过焦点而垂直于对称轴的弦AB,称为抛物线的通径,
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
|AB|=2p
通径
5、
2p越大,抛物线张口越大.
方程 图形 准线 焦点 对称轴
x轴
x轴
y轴
y轴
P(x,y)
P(x,y)
P(x,y)
O
探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是抛物镜面.
抛物镜面:抛物线绕其对称轴旋转而成的曲面.
灯泡放在抛物线的焦点位置上,通过镜面反射就
变成了平行光束,这就是探照灯、汽车前灯、手电筒
的设计原理.
平行光线射到抛物镜面上,经镜面反射后,反射光
线都经过抛物线的焦点,这就是太阳灶能把光能转化为
热能的理论依据.
归纳:
(1)、抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2)、抛物线只有一条对称轴,没有对称中心;
(3)、抛物线只有一个顶点,一个焦点,一条准线;
(4)、抛物线的离心率是确定的,为1,
⑸、抛物线的通径为2P, 2p越大,抛物线的张口越大.
解法1:
例1:斜率为1的直线l 经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点,求线段AB的长.
三、典例精析
由抛物线方程
焦点F的坐标;
又k=1
直线l 的方程;
联立方程
A、B的坐标;
运用两点间的距离公式
求|AB|的值.
运算复杂
解法2:
由已知,
p=2,
焦点F(1,0),
∴直线AB的方程为
联立方程
故 |AB|=8.
O
x
y
例1:斜率为1的直线l 经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点,求线段AB的长.
准线: x=-1,
F
x=-1
A
B
设A(x1, y1)、B (x2, y2), 则
消去y得:
归纳:
O
x
y
F
M
N
(1)、抛物线的焦半径公式
(2)、抛物线的焦点弦长公式
(1)已知点A(-2,3)与抛物线y2=2px (p>0)的焦点
的距离是5,则P= .
(2)抛物线y2=4x 的弦AB垂直x轴,若|AB|= ,则
焦点到AB的距离为 .
4
2
(3)已知直线x-y=2与抛物线y2=4x 交于A、B两点,
那么线段AB的中点 坐标是 .
课堂练习
y
x
o
例2、正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px (p>0)上,求这个三角形的边长.
解:如图,设正三角形OAB的顶点A、B在抛物线上,且坐标分别为(x1,y1)、(x2,y2), 则
y12=2px1
y22=2px2
分析:
观察图形,正三角形和抛物线都是轴对称图形,
点A、B关于x轴对称,
必须加以证明!
即证A、B的横坐标相等,纵坐标互为相反数.
A
B
又|OA|=|OB|,所以x12+y12=x22+y22
y
x
o
A
B
由此可得|y1|=|y2|,
∵ x1>0,x2>0,2p>0, ∴ x1=x2
所以由
即线段AB关于x轴对称,
因为x轴垂直于AB,
(x1-x2)(x1+x2+2p)=0.
(x12-x22)+2p(x1-x2)=0,
即 :x12-x22+2px1-2px2=0,
又|OA|=|OB|,所以x12+y12=x22+y22
1、一个正三角形的三个顶点,都在抛物线
上,其中一个顶点为坐标原点,则这个三角形的
面积为 .
课堂练习
五、归纳总结
抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
抛物线只有一条对称轴,没有对称中心;
抛物线的离心率是1;
抛物线只有一个顶点;
抛物线的通径为2P,通径越大抛物线的张口越大.
1、范围:
2、对称性:
3、顶点:
4、离心率:
5、通径:
6、光学性质:
从焦点出发的光线,通过抛物线反射就变成了平行光束.
