6.1平行四边形及其性质第1课时课件(共21张PPT)
文档属性
| 名称 | 6.1平行四边形及其性质第1课时课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 169.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-28 00:00:00 | ||
图片预览








文档简介
课件21张PPT。§6.1平行四边形及其性质(1) 第六章:平行四边形请同学们认真阅读课本第4页,完成以下内容:1、什么叫平行四边形?怎么表示?如何读法?两组对边分别平行的四边形叫做平行四边形.平行四边形不相邻的两个顶
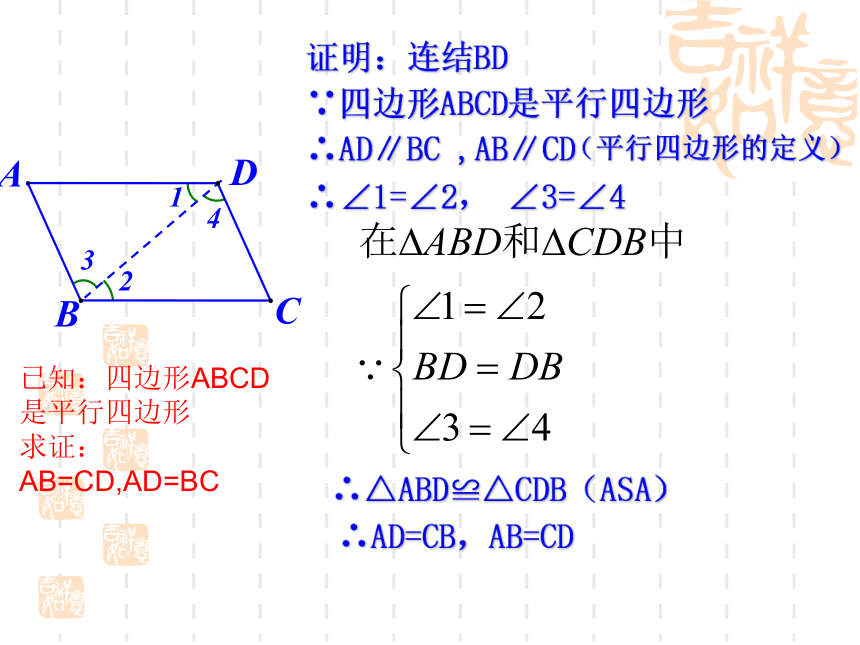
点连成的线段叫它的对角线.如图2所示的四边形ABCD是平行四边形.读作:平行四边形ABCD几何语言:∵四边形ABCD是平行四边形∴四边形ABCD是平行四边形平行四边形对边分别平行的四边形对平行四边形的理解:猜想:平行四边形的对边有什么样的关系?平行四边形对边相等.(1)根据题意,画出图形。(2)结合图形,写出已知、求证。(3)找出由已知推出求证的途径,写出证明。二证明:连结BD
∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形的定义)∴∠1=∠2, ∠3=∠4∴△ABD≌△CDB(ASA)∴AD=CB,AB=CD
4123DCBA已知:四边形ABCD是平行四边形
求证:AB=CD,AD=BC例1:(1)夹在两条平行直线间的平行线段相等。(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等。如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:∵ 四边形ABCD是平行四边形
∴CD=AB=8m, AD=BC(平行四边形对边相等)
又AB+BC+CD+AD=36,
即2AB+2BC=36
∴ AD=BC=10m练习1:8cm如图,若BE平分∠ABC,则ED= .4cm5cm5cm4cm练习2:平行线角平分线等腰三角形+猜想:平行四边形的对角有什么样的关系?平行四边形对角相等.证明:连结BD
∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形定义)∴∠1=∠2, ∠3=∠4(两直线平行,
内错角相等)∴△ABD≌△CDB(ASA)∴AD=CB,AB=CD(全等三角形对应边相等)
∠A=∠C (全等三角形对应角相等)
∵∠1=∠2, ∠3=∠4∴∠1+∠4=∠2+∠3(等式性质)即∠ABC=∠ADC∴ ∠A=∠C,∠ABC=∠ADC4123DCBA已知:四边形ABCD是平行四边形
求证:∠A=∠C,∠ABC=∠ADC
平行四边形的性质定理2:平行四边形对角相等.例2:如图,在平行四边形ABCD中,已知 ∠A=50°,求其他各内角。解∵四边形ABCD是平行四边形
∴ ∠C= ∠A=50°∵AD‖BC
∴∠D=∠B=130° -∠C= 50°
(平行四边形对角相等).∴ ∠B=180°-∠A=180°-50°=130° 练习3、给出四边形ABCD的四个内角∠A、∠B、∠C、∠D的度数之比,则比为哪一组时,四边形ABCD为平行四边形( )
A1:2:3:4 B2:2:3:4
C2:3:2:3 D2:3:3:2C练习4:练习4.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;(2)边AB,BC的长度.解:(1)∵四边形ABCD是平行四边形∴∠B=∠ADC(平行四边形对角相等)
AB∥CD(平行四边形对边平行)∴∠B+∠BCD=180°
(两直线平行,同旁内角互补)∵∠B=56°∴∠ADC=∠B=56°∠BCD=180°-∠B=180°-56°=124°(2)∵四边形ABCD是平行四边形∴AD=BC,AB=CD(平行四边形对边相等)∵AD=30,CD=25 ∴BC=30,AB=25.练习5:挑战自我练习6:课本第6页的练习课堂小结:
2、平行四边形有哪些性质?1、什么是平行四边形?
性质2:平行四边形对角相等.两组对边分别平行的四边形叫做平行四边形.性质1:平行四边形对边相等.
点连成的线段叫它的对角线.如图2所示的四边形ABCD是平行四边形.读作:平行四边形ABCD几何语言:∵四边形ABCD是平行四边形∴四边形ABCD是平行四边形平行四边形对边分别平行的四边形对平行四边形的理解:猜想:平行四边形的对边有什么样的关系?平行四边形对边相等.(1)根据题意,画出图形。(2)结合图形,写出已知、求证。(3)找出由已知推出求证的途径,写出证明。二证明:连结BD
∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形的定义)∴∠1=∠2, ∠3=∠4∴△ABD≌△CDB(ASA)∴AD=CB,AB=CD
4123DCBA已知:四边形ABCD是平行四边形
求证:AB=CD,AD=BC例1:(1)夹在两条平行直线间的平行线段相等。(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等。如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:∵ 四边形ABCD是平行四边形
∴CD=AB=8m, AD=BC(平行四边形对边相等)
又AB+BC+CD+AD=36,
即2AB+2BC=36
∴ AD=BC=10m练习1:8cm如图,若BE平分∠ABC,则ED= .4cm5cm5cm4cm练习2:平行线角平分线等腰三角形+猜想:平行四边形的对角有什么样的关系?平行四边形对角相等.证明:连结BD
∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形定义)∴∠1=∠2, ∠3=∠4(两直线平行,
内错角相等)∴△ABD≌△CDB(ASA)∴AD=CB,AB=CD(全等三角形对应边相等)
∠A=∠C (全等三角形对应角相等)
∵∠1=∠2, ∠3=∠4∴∠1+∠4=∠2+∠3(等式性质)即∠ABC=∠ADC∴ ∠A=∠C,∠ABC=∠ADC4123DCBA已知:四边形ABCD是平行四边形
求证:∠A=∠C,∠ABC=∠ADC
平行四边形的性质定理2:平行四边形对角相等.例2:如图,在平行四边形ABCD中,已知 ∠A=50°,求其他各内角。解∵四边形ABCD是平行四边形
∴ ∠C= ∠A=50°∵AD‖BC
∴∠D=∠B=130° -∠C= 50°
(平行四边形对角相等).∴ ∠B=180°-∠A=180°-50°=130° 练习3、给出四边形ABCD的四个内角∠A、∠B、∠C、∠D的度数之比,则比为哪一组时,四边形ABCD为平行四边形( )
A1:2:3:4 B2:2:3:4
C2:3:2:3 D2:3:3:2C练习4:练习4.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;(2)边AB,BC的长度.解:(1)∵四边形ABCD是平行四边形∴∠B=∠ADC(平行四边形对角相等)
AB∥CD(平行四边形对边平行)∴∠B+∠BCD=180°
(两直线平行,同旁内角互补)∵∠B=56°∴∠ADC=∠B=56°∠BCD=180°-∠B=180°-56°=124°(2)∵四边形ABCD是平行四边形∴AD=BC,AB=CD(平行四边形对边相等)∵AD=30,CD=25 ∴BC=30,AB=25.练习5:挑战自我练习6:课本第6页的练习课堂小结:
2、平行四边形有哪些性质?1、什么是平行四边形?
性质2:平行四边形对角相等.两组对边分别平行的四边形叫做平行四边形.性质1:平行四边形对边相等.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
