2.4线段的垂直平分线课件(共18张PPT)
文档属性
| 名称 | 2.4线段的垂直平分线课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 164.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-28 00:00:00 | ||
图片预览




文档简介
课件18张PPT。§2.4.1线段的垂直平分线上节课我们学会了什么?一个图形的一部分,以某条直线为对称轴,经过轴对称能与图形的另一部分___________,这样的图形叫做_________________.重合轴对称图形二轴对称图形和轴对称的区别与联系区别:轴对称图形是指一个具有特殊形状的图形;两个图形关于某一条直线成轴对称是指两个图形的特殊形状和位置关系。联系: ①都有一条直线,都沿直线折叠重合;②若把轴对称图形沿对称轴分成两部分,则这两个图形关于这条直线成轴对称;若把两个关于某直线成轴对称的图形看作一个整体,则它就是一个轴对称图形。一 轴对称图形的定义实验与探究如图,在纸上画一条线段AB,通过对折后点A与点B重合,思考下列问题,与同学交流。
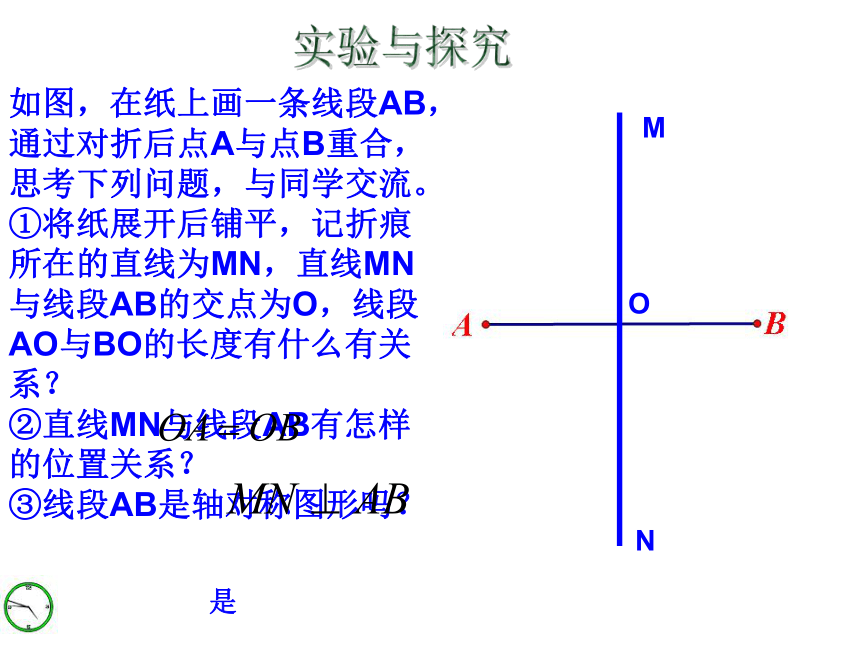
①将纸展开后铺平,记折痕所在的直线为MN,直线MN与线段AB的交点为O,线段AO与BO的长度有什么有关系?
②直线MN与线段AB有怎样的位置关系?
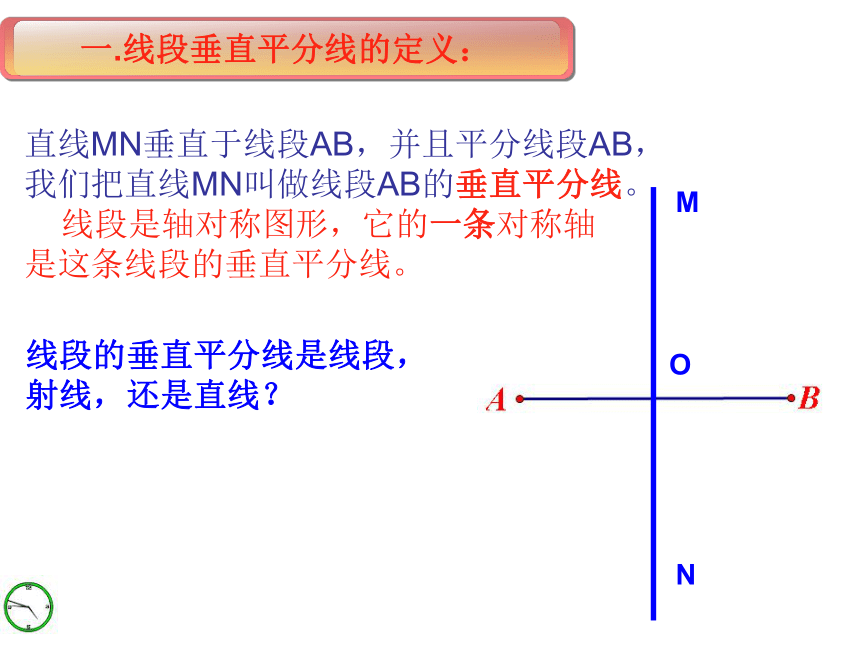
③线段AB是轴对称图形吗?MNO是直线MN垂直于线段AB,并且平分线段AB,
我们把直线MN叫做线段AB的垂直平分线。
线段是轴对称图形,它的一条对称轴
是这条线段的垂直平分线。MON线段的垂直平分线是线段,
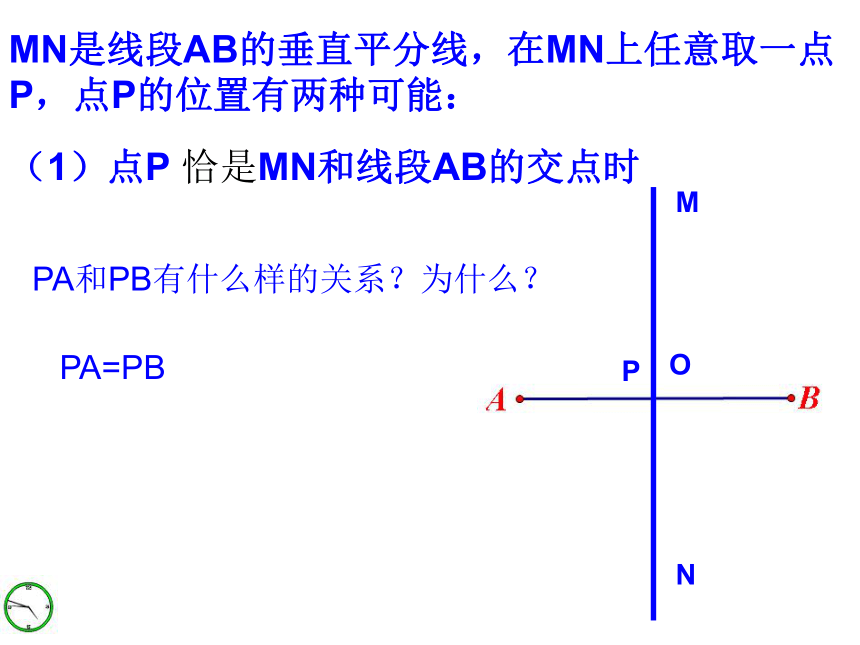
射线,还是直线?MONMN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:(1)点P 恰是MN和线段AB的交点时PPA和PB有什么样的关系?为什么?PA=PBMNMN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:(2)点P 不在线段AB上时PPA和PB有什么样的关系?为什么?PA=PB线段垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等综合(1)(2)可得:一.线段垂直平分线的性质线段垂直平分线上的点到线段两端的距离相等。MNPO几何语言1:∵PC⊥AB,AC=BC(已知)∴PA=PB(线段垂直平分线上的点到线段两端的距离相等。 )几何语言2:∵MN垂直平分AB(已知)∴PA=PB(线段垂直平分线上的点到线段两端点的距离相等。 )例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:PA=PB=PC;证明:
∵MN垂直平分AB
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.练习1:课本练习1和2看作业精编22页结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:PA=PB=PC;证明:
∵MN垂直平分AB
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.以点P为圆心,PA为半径,圆恰好经过三个顶点,此圆称为△ABC的外接圆,因此圆心称为外心。外心的性质是什么?到三角形三个顶点的距离相等。到三角形三个顶点的距离相等的点是什么的交点?三角形三条边垂直平分线的交点。这节课我们学会了什么?直线MN垂直于线段AB,并且平分线段AB,
我们把直线MN叫做线段AB的垂直平分线。
线段是轴对称图形,它的一条对称轴
是这条线段的垂直平分线。二 线段垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等习题1.2 A组
①将纸展开后铺平,记折痕所在的直线为MN,直线MN与线段AB的交点为O,线段AO与BO的长度有什么有关系?
②直线MN与线段AB有怎样的位置关系?
③线段AB是轴对称图形吗?MNO是直线MN垂直于线段AB,并且平分线段AB,
我们把直线MN叫做线段AB的垂直平分线。
线段是轴对称图形,它的一条对称轴
是这条线段的垂直平分线。MON线段的垂直平分线是线段,
射线,还是直线?MONMN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:(1)点P 恰是MN和线段AB的交点时PPA和PB有什么样的关系?为什么?PA=PBMNMN是线段AB的垂直平分线,在MN上任意取一点P,点P的位置有两种可能:(2)点P 不在线段AB上时PPA和PB有什么样的关系?为什么?PA=PB线段垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等综合(1)(2)可得:一.线段垂直平分线的性质线段垂直平分线上的点到线段两端的距离相等。MNPO几何语言1:∵PC⊥AB,AC=BC(已知)∴PA=PB(线段垂直平分线上的点到线段两端的距离相等。 )几何语言2:∵MN垂直平分AB(已知)∴PA=PB(线段垂直平分线上的点到线段两端点的距离相等。 )例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:PA=PB=PC;证明:
∵MN垂直平分AB
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.练习1:课本练习1和2看作业精编22页结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:PA=PB=PC;证明:
∵MN垂直平分AB
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.以点P为圆心,PA为半径,圆恰好经过三个顶点,此圆称为△ABC的外接圆,因此圆心称为外心。外心的性质是什么?到三角形三个顶点的距离相等。到三角形三个顶点的距离相等的点是什么的交点?三角形三条边垂直平分线的交点。这节课我们学会了什么?直线MN垂直于线段AB,并且平分线段AB,
我们把直线MN叫做线段AB的垂直平分线。
线段是轴对称图形,它的一条对称轴
是这条线段的垂直平分线。二 线段垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等习题1.2 A组
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
