青岛版七年级数学上册1.2几何图形课件(28张PPT)
文档属性
| 名称 | 青岛版七年级数学上册1.2几何图形课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 353.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-29 00:00:00 | ||
图片预览






文档简介
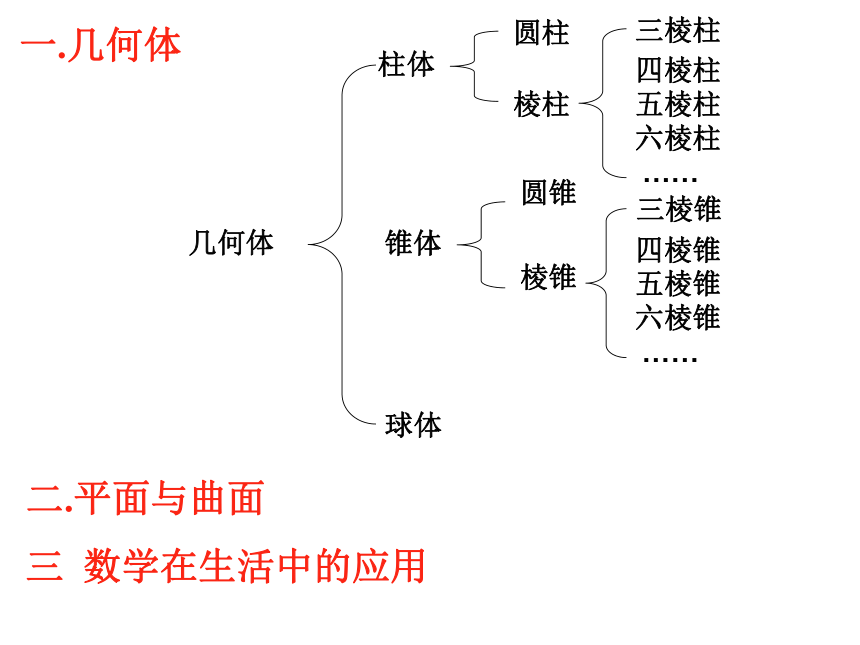
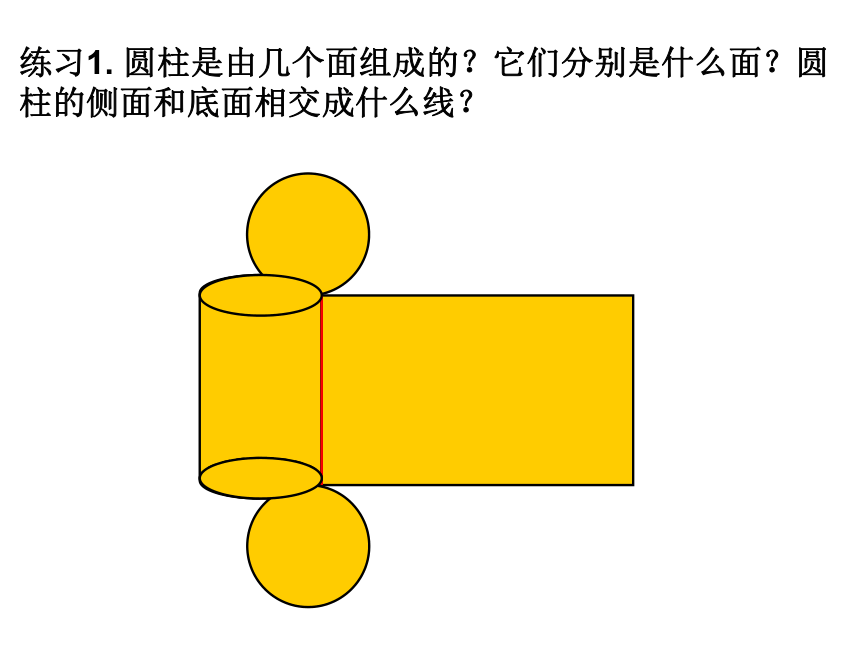
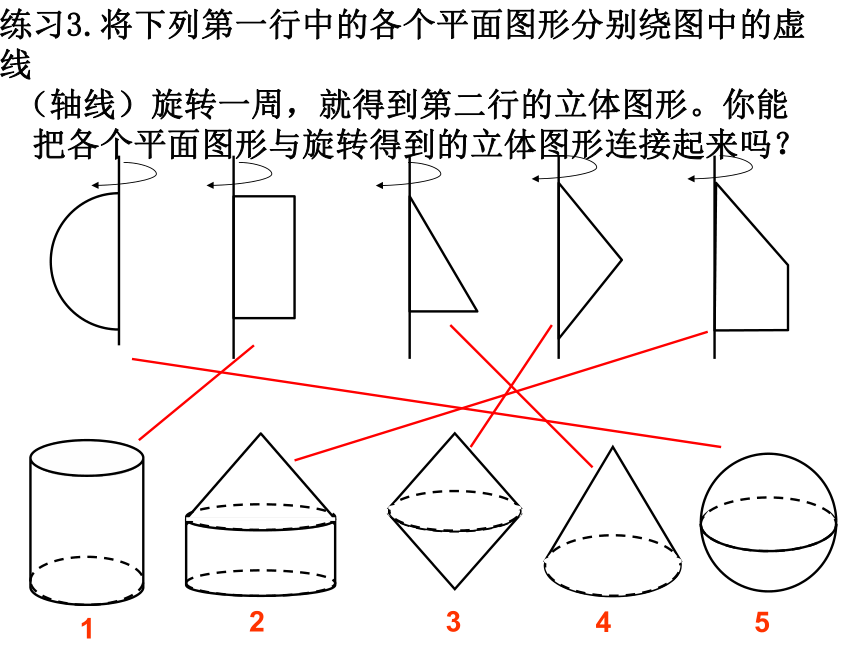
课件28张PPT。§1.2 几何图形上节课我们学习了什么?一.几何体二.平面与曲面三 数学在生活中的应用几何体柱体锥体球体圆柱棱柱三棱柱四棱柱五棱柱六棱柱……圆锥棱锥三棱锥四棱锥五棱锥六棱锥……阅读第7页的“观察与思考”并回答下面的问题。一.几何体的构成元素练习1. 圆柱是由几个面组成的?它们分别是什么面?圆柱的侧面和底面相交成什么线?观察下面的图片,你发现了什么?点动成线面动成体线动成面OABA旋转门做课本第9页的练习第1题和第2题。练习2:练习3.将下列第一行中的各个平面图形分别绕图中的虚线
(轴线)旋转一周,就得到第二行的立体图形。你能
把各个平面图形与旋转得到的立体图形连接起来吗?12345三 正方体的表面展开图 例3:将包装盒沿它的某些棱剪开,并铺在平面上。得到一个怎样的平面图形?如果展开的方法不同,得到的图形相同吗?动手做一做,然后画一画。你能得到多少种平面图形?与同学交流。
1234第一类,中间四连方,两侧各一个,共六种。称为“141”型.第二类,中间三连方,两侧各有一、二个,共三种。称为“231” 第三类, 阶梯型两行只能有1个正方形相连.2,2,2型3,3型不能出现田字格!!!××判断下列图形能不能折成正方体?(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)四. 找对面题型你还记得正方体的展开图怎样找对面吗?例4:隔面有面是对面,隔面无面就拐弯123456123456当堂训练1. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数相等,求:271练习4:2.“坚”在下,“就”在后,胜利在哪里? “胜”在上,
“利”在前! 3.由带标志的正方体图去判断是否属于它的展开图
如下图,正方体三个侧面分别画有不同图案,
它的展开图可以是( ).C一.几何体的构成元素点,线,面,体。点动成线面动成体线动成面二.三 . 正方体的表面展开图隔面有面是对面,隔面无面就拐弯四. 正方体的表面展开图找对面的规律11种
(轴线)旋转一周,就得到第二行的立体图形。你能
把各个平面图形与旋转得到的立体图形连接起来吗?12345三 正方体的表面展开图 例3:将包装盒沿它的某些棱剪开,并铺在平面上。得到一个怎样的平面图形?如果展开的方法不同,得到的图形相同吗?动手做一做,然后画一画。你能得到多少种平面图形?与同学交流。
1234第一类,中间四连方,两侧各一个,共六种。称为“141”型.第二类,中间三连方,两侧各有一、二个,共三种。称为“231” 第三类, 阶梯型两行只能有1个正方形相连.2,2,2型3,3型不能出现田字格!!!××判断下列图形能不能折成正方体?(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)四. 找对面题型你还记得正方体的展开图怎样找对面吗?例4:隔面有面是对面,隔面无面就拐弯123456123456当堂训练1. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数相等,求:271练习4:2.“坚”在下,“就”在后,胜利在哪里? “胜”在上,
“利”在前! 3.由带标志的正方体图去判断是否属于它的展开图
如下图,正方体三个侧面分别画有不同图案,
它的展开图可以是( ).C一.几何体的构成元素点,线,面,体。点动成线面动成体线动成面二.三 . 正方体的表面展开图隔面有面是对面,隔面无面就拐弯四. 正方体的表面展开图找对面的规律11种
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
