锐角三角函数--正弦
图片预览


文档简介
课件13张PPT。义务教育课程标准实验教科书(数学)九年级下册锐角三角函数
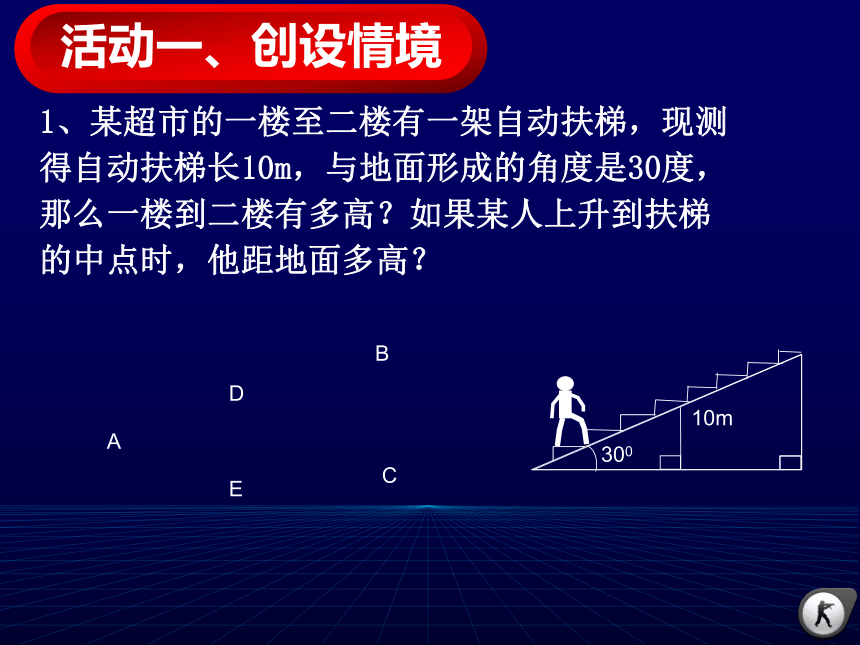
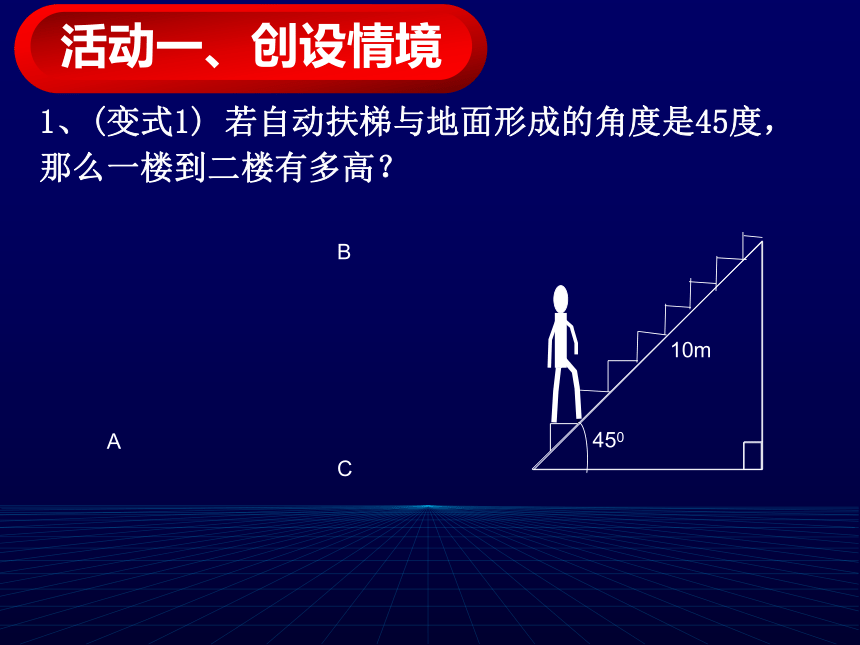
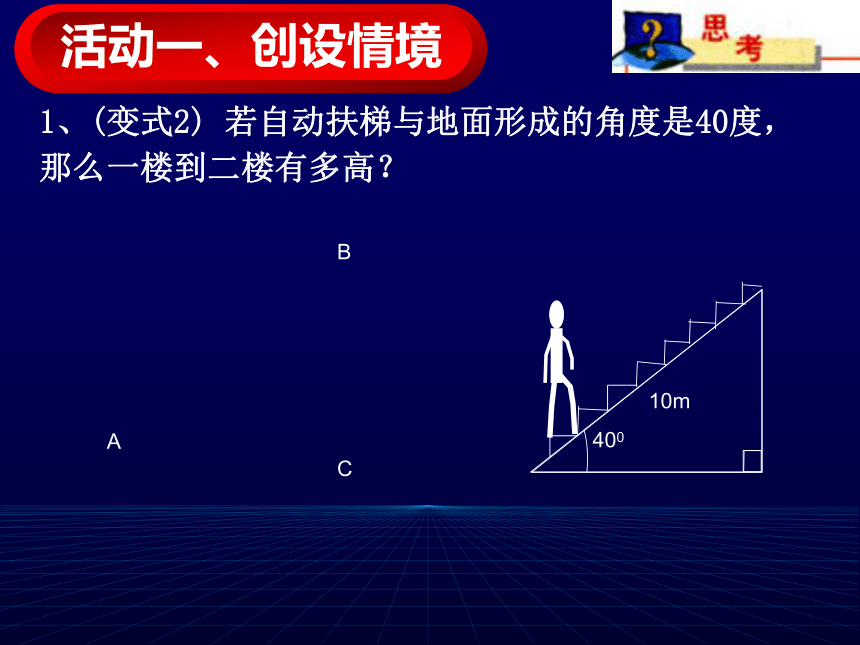
正弦新余四中 周峰1、某超市的一楼至二楼有一架自动扶梯,现测得自动扶梯长10m,与地面形成的角度是30度,那么一楼到二楼有多高?如果某人上升到扶梯的中点时,他距地面多高? 活动一、创设情境ABCDE1、(变式1) 若自动扶梯与地面形成的角度是45度,那么一楼到二楼有多高?45010mABC活动一、创设情境1、(变式2) 若自动扶梯与地面形成的角度是40度,那么一楼到二楼有多高?40010mABC活动一、创设情境 1、请同学们画一个含30度角的直角三角形,测量30度角的对边和斜边的长度,并计算它们的比值 。
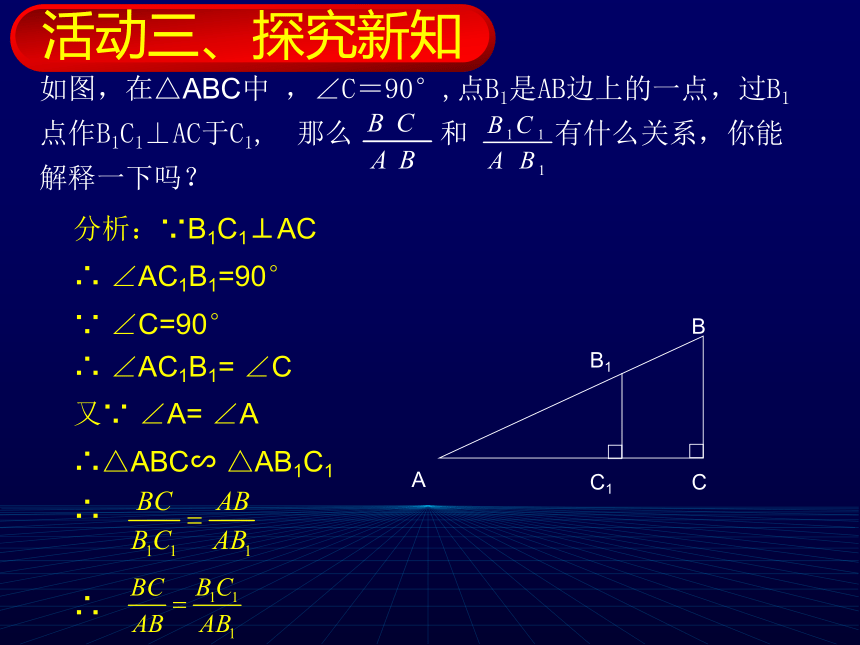
2、请同学们画一个含40度角的直角三角形,测量40度角的对边与斜边的长度,并计算它们的比值。活动2活动二、实践探索如图,在△ABC中 ,∠C=90°,点B1是AB边上的一点,过B1点作B1C1⊥AC于C1, 那么 和 有什么关系,你能解释一下吗?活动三、探究新知分析:∵B1C1⊥AC
∴ ∠AC1B1=90°
∵ ∠C=90°
∴ ∠AC1B1= ∠C
又∵ ∠A= ∠A
∴△ABC∽ △AB1C1
∴
∴
在Rt?ABC中,∠C=900,我们把锐角A的对边与斜边的比值叫做∠A的正弦,记作sinA
即
A注意事项:1、 sinA不是sin 与A的乘积,而是一个整体;
2、正弦的三种表示方式:sinA、sin56°、sin∠DEF;
3、sinA是线段之间的一个比值,没有单位。
4、相同或相等的锐角,它们的正弦值也相等。活动三、探究新知如图,在Rt?ABC中,∠C=900,求sinA和sinB的值。例题活动四、例题分析解:1、抢答题(1)如图、在Rt?ABC中, ∠C=900,则
①sin300= ,sin600 = 。
②sin450= 。
活动五、巩固练习(2)如图,已知点P的坐标是(3、 ),
则sinα的值是 。(3)如图、在Rt?ABC中, CD是斜边AB上的高,则下列线段比中不等于 sinA的是( )2、在Rt?ABC中, ∠C=900,BC=2, ,求AC的长。
3、在Rt?ABC中, ∠C=900, sinA= , 求sinB的值。 D活动五、巩固练习 1、学生小结
(1)这堂课学习的主要内容是什么?
(2)在这堂课中应注意哪些问题?
(3)这堂课中我有哪些收获和看法与大家交流。
活动六、归纳小结(1)在直角三角形中当锐角固定时,它的对边与斜边的比值也是固定的,进而得出正弦函数的定义,即在Rt?ABC中,我们把锐角A的对边与斜边的比值叫做角A的正弦,记作sinA
即
(2)这节课我们探讨的是锐角三角函数中正弦函数,它反映的是直角三角形中当锐角固定时,它的对边与斜边的比值也固定,那么我们可以想象一下锐角的邻边与斜边的比值是否固定?对边与邻边的比值是否固定?活动六、归纳小结2、教师小结谢谢大家光临指导!谢谢大家光临指导!2009.10
正弦新余四中 周峰1、某超市的一楼至二楼有一架自动扶梯,现测得自动扶梯长10m,与地面形成的角度是30度,那么一楼到二楼有多高?如果某人上升到扶梯的中点时,他距地面多高? 活动一、创设情境ABCDE1、(变式1) 若自动扶梯与地面形成的角度是45度,那么一楼到二楼有多高?45010mABC活动一、创设情境1、(变式2) 若自动扶梯与地面形成的角度是40度,那么一楼到二楼有多高?40010mABC活动一、创设情境 1、请同学们画一个含30度角的直角三角形,测量30度角的对边和斜边的长度,并计算它们的比值 。
2、请同学们画一个含40度角的直角三角形,测量40度角的对边与斜边的长度,并计算它们的比值。活动2活动二、实践探索如图,在△ABC中 ,∠C=90°,点B1是AB边上的一点,过B1点作B1C1⊥AC于C1, 那么 和 有什么关系,你能解释一下吗?活动三、探究新知分析:∵B1C1⊥AC
∴ ∠AC1B1=90°
∵ ∠C=90°
∴ ∠AC1B1= ∠C
又∵ ∠A= ∠A
∴△ABC∽ △AB1C1
∴
∴
在Rt?ABC中,∠C=900,我们把锐角A的对边与斜边的比值叫做∠A的正弦,记作sinA
即
A注意事项:1、 sinA不是sin 与A的乘积,而是一个整体;
2、正弦的三种表示方式:sinA、sin56°、sin∠DEF;
3、sinA是线段之间的一个比值,没有单位。
4、相同或相等的锐角,它们的正弦值也相等。活动三、探究新知如图,在Rt?ABC中,∠C=900,求sinA和sinB的值。例题活动四、例题分析解:1、抢答题(1)如图、在Rt?ABC中, ∠C=900,则
①sin300= ,sin600 = 。
②sin450= 。
活动五、巩固练习(2)如图,已知点P的坐标是(3、 ),
则sinα的值是 。(3)如图、在Rt?ABC中, CD是斜边AB上的高,则下列线段比中不等于 sinA的是( )2、在Rt?ABC中, ∠C=900,BC=2, ,求AC的长。
3、在Rt?ABC中, ∠C=900, sinA= , 求sinB的值。 D活动五、巩固练习 1、学生小结
(1)这堂课学习的主要内容是什么?
(2)在这堂课中应注意哪些问题?
(3)这堂课中我有哪些收获和看法与大家交流。
活动六、归纳小结(1)在直角三角形中当锐角固定时,它的对边与斜边的比值也是固定的,进而得出正弦函数的定义,即在Rt?ABC中,我们把锐角A的对边与斜边的比值叫做角A的正弦,记作sinA
即
(2)这节课我们探讨的是锐角三角函数中正弦函数,它反映的是直角三角形中当锐角固定时,它的对边与斜边的比值也固定,那么我们可以想象一下锐角的邻边与斜边的比值是否固定?对边与邻边的比值是否固定?活动六、归纳小结2、教师小结谢谢大家光临指导!谢谢大家光临指导!2009.10
