必修1最值求法

函数最值（值域）的求法
求函数最值的常用方法有：直接法、公式法、配方法、单调法、换元法、判别式法、图象法、数形结合法、分离常数法等.
温馨提示：函数的最值问题实质上是函数的值域问题，因此求函数最值的方法，也是求函数的值域的方法，只是答题的方式有所差异。
1、直接法：从自变量x的范围出发，推出y=f(x)的取值范围，从而求得最值。
例1：求函数的最值。
解：∵，∴，
∴函数的最小值为1。
2、公式法：求二次函数的最值时（对称轴在定义域内），应用最值公式，直接写出其最值。
EX:求函数y=x2+x的最小值。
注意：函数的最大（小）值，实际上是函数图像的最高（低）点的纵坐标，因而可借助函数图像的直观性，可得到函数的最值。
3、配方法：二次函数的有关性质、图象作出分析，特别是求某一给定区间的最值与值域。此方法一般可解决形如 (a≠0)的函数的值域与最值。
例2：求函数（）的最值。
解：，
∵，∴，∴
∴，∴
∴函数（）的最小值为，最大值为5。
4、单调法：先判断函数的单调性，再利用单调性求最值。
一般，我们常用到下面的结论：
①如果函数f(x)在区间(a,b]上单调递减，在区间[b,c)上单调递增，则函数y=f(x)在x=b处有最小值f(b)。
②如果函数f(x)在区间(a,b]上单调递增，在区间[b,c)上单调递减，则函数y=f(x)在x=b处有最大值f(b)。
③如果函数f(x)在闭区间[a,b]上单调递增(减)，则在区间的两端点处分别取得最小(大)值和最大(小)值.
注意:任意一个单调函数在其限定的闭区间上存在最值，并在两个端点处取得。但是，要注意是函数的单调性改变的点是不是在这个限定的闭区间内，不要单纯的认为 f(a) 、f(b)分别就是最大值和最小值。
例3 已知函数 ，求函数的最值。
具体答案见课本31页。
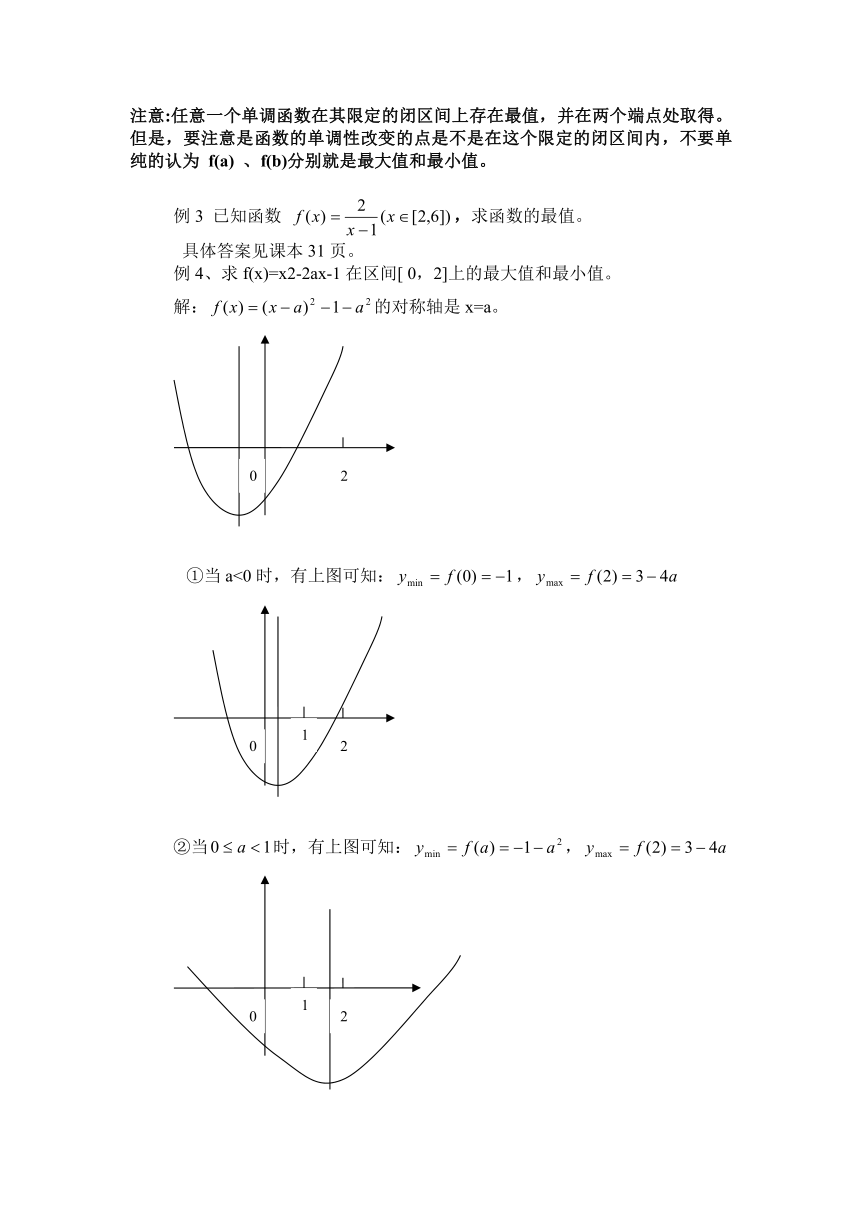
例4、求f(x)=x2-2ax-1在区间[ 0，2]上的最大值和最小值。
解：的对称轴是x=a。
①当a<0时，有上图可知：，
②当时，有上图可知：，
③当时，，
④当时，，
5、换元法：运用代数代换，将所给函数化成值域容易确定的另一函数，从而求得原函数的最值，形如（、、、均为常数，且）的函数常用此法求解。常用设 ，利用换元法转化为求二次函数等常见函数的最值问题，此时要注意换元后函数的定义域。
例5：求函数的最值。
解：令（），则，
∴
当，即时，，无最小值。
6、图像法：能够画出函数的图象，可以依据函数最值的几何意义，借助图象写出最值。其步骤是：①画函数的图象；②观察函数的图象，找出图象的最高点和最低点，并确定它们的纵坐标；③由最高点和最低点的纵坐标写出函数的最值。
例6：求函数的最值。
解：∵ ，
∴的图像如图所示，
由图像知：函数的最小值为8。
7、数形结合：如果函数的解析式含有绝对值或根号，那么能将函数的解析式赋予几何意义，结合图形利用其几何意义求最值。
其步骤是：①对函数的解析式赋予几何意义;②将函数的最值问题转化成几何问题；③应用几何知识求最值。
例7：求函数的最值。
函数的解析式的几何意义是：P是数轴上的任意一点，P到的对应点A、B的距离的和，即，如图所示：
观察数轴，可得，即函数由最小值2，无最大值。
0
1
P A P B P
2
0
1
2
0
1
2
0
1
2
0