沪教版七年级数学下册 16.1 相交线(含解析)
文档属性
| 名称 | 沪教版七年级数学下册 16.1 相交线(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-11 22:57:05 | ||
图片预览



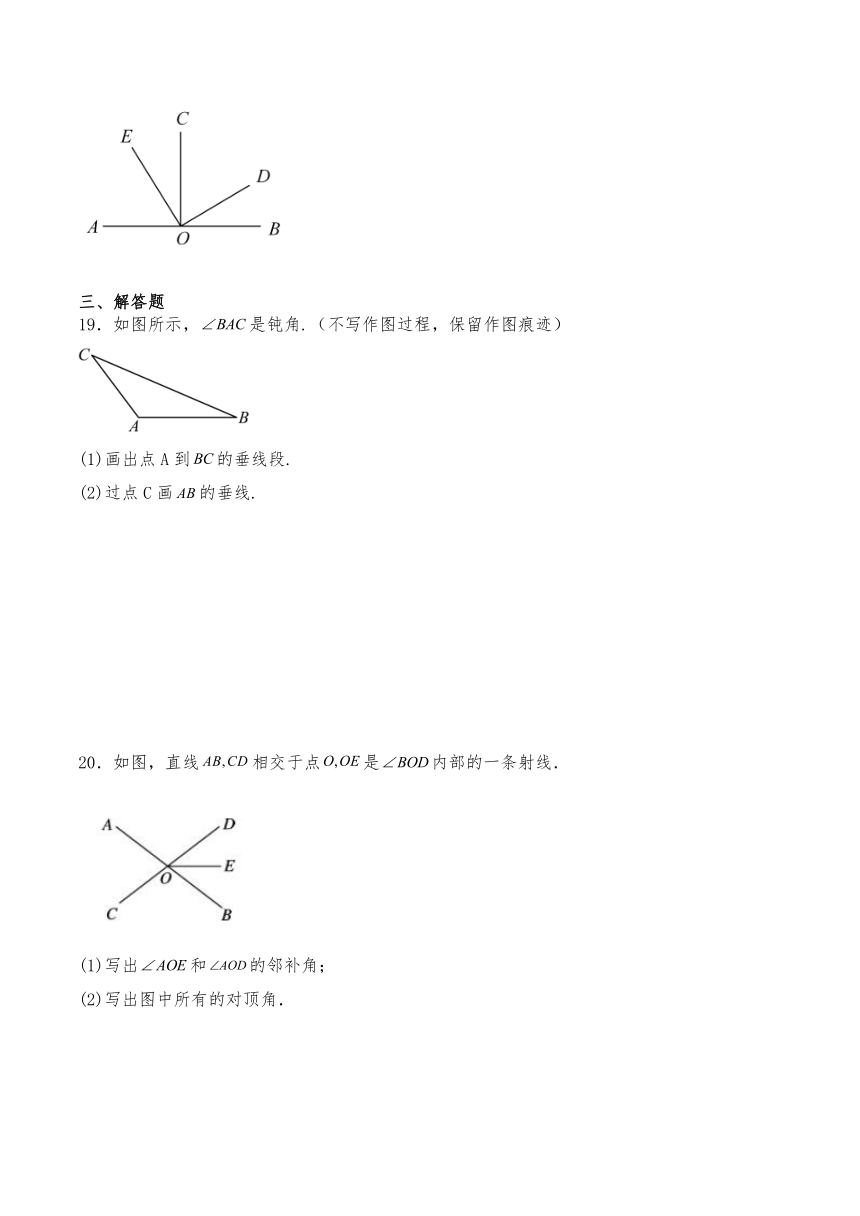
文档简介
16.1 相交线
一、单选题
1.下面四个图形中,与是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
2.下列图形中,∠1与∠2互为邻补角的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.互补的两个角是邻补角 B.相等的角必是对顶角
C.对顶角一定相等 D.若两个角不是对顶角,则这两个角不相等
4.如图,已知直线与相交于点F,平分,若,则度数是( )
A. B. C. D.
5.如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型,固定木条a,转动木条b,当减小时,下列说法正确的是( )
A.增大 B.增大 C.减小 D.与的和增大
6.下列说法中正确的个数有( )
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短.
(2)画一条直线的垂线段可以画无数条.
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离.
A.1个 B.2个 C.3个 D.4个
7.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3的度数为( )
A.90° B.180° C.270° D.360°
8.如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=∠COE,∠DOE=72°.则∠COE的度数是( )
A.36° B.72° C.44° D.56°
9.如图,为直线上一点,,OE平分,OG平分,OF平分,下列结论:①;②与互补;③;④,其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
10.如图,2条直线 最多有=1个交点,3条直线最多有=3个交点,4条直线最多有=6个交点,……由此猜想,8条直线最多有___个交点.
A.32 B.16 C.28 D.40
二、填空题
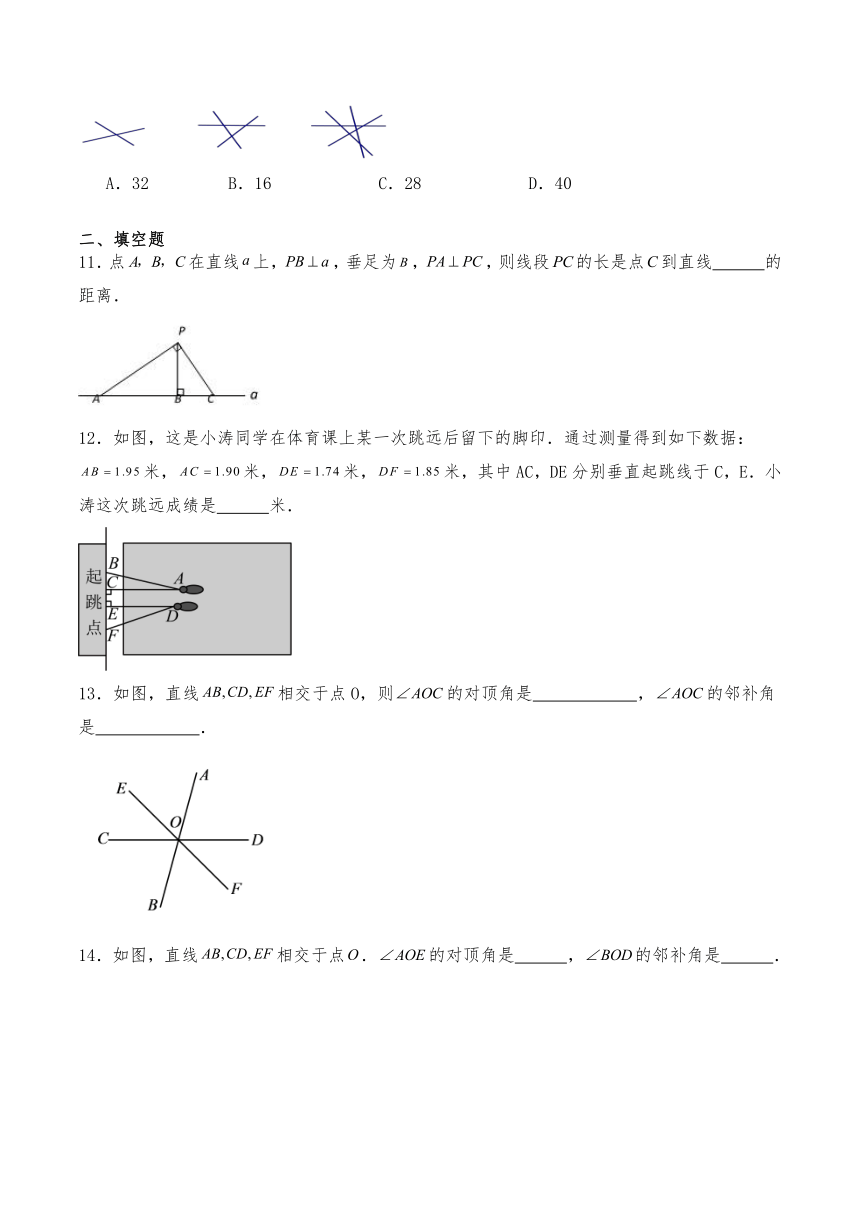
11.点在直线上,,垂足为,,则线段的长是点到直线 的距离.
12.如图,这是小涛同学在体育课上某一次跳远后留下的脚印.通过测量得到如下数据:米,米,米,米,其中AC,DE分别垂直起跳线于C,E.小涛这次跳远成绩是 米.
13.如图,直线相交于点O,则的对顶角是 ,的邻补角是 .
14.如图,直线相交于点.的对顶角是 ,的邻补角是 .
15.如图,点O是直线上一点,,是的平分线,则的度数是 °.
16.如图,直线、相交于点O,平分,平分,且,则的度数为 .
17.如图,直线相交于点O,.
(1)图中的对顶角有 对;
(2)的邻补角是 ;
(3)如果,,那么 .
18.如图,已知直线,作,垂足为,在内部,在内部,且,,则的度数为 .
三、解答题
19.如图所示,是钝角.(不写作图过程,保留作图痕迹)
(1)画出点A到的垂线段.
(2)过点C画的垂线.
20.如图,直线相交于点是内部的一条射线.
(1)写出和的邻补角;
(2)写出图中所有的对顶角.
21.如图,已知于,于.
(1)点到直线的距离是线段_______的长;
(2)点到直线的距离是线段_______的长;
(3)线段的长表示点到直线_______距离;
(4)线段的长表示点到直线_______距离;
(5)线段的长表示点_______到直线______距离;
(6)线段的长表示点_______到直线______距离;
22.如图,直线和直线相交于点,平分.
(1)写出图中的对顶角______,和两个邻补角______;
(2)若,求的度数.
23.按下列要求画图并填空:如图,直线AB与CD相交于点O,P是CD上的一点.
(1)过点P画出CD的垂线,交直线AB于点E;
(2)过点P画PF⊥AB,垂足为点F;
(3)点O到直线PE的距离是线段 的长;
(4)点P到直线CD的距离为 .
24.按下列要求画图并填空:如图,
(1)过点A画直线BC的平行线AD;
(2)过点B画直线AD的垂线段,垂足为点E;
(3)若点B到直线AD的距离为4,BC=2,则= .
25.如图,直线与相交于点,,,射线平分,求的度数.
26.如图,直线AB,CD相交于点O,OA平分.
(1)的对顶角为________;
(2)若,求的度数;
(3)若,求的度数.
27.如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.
解:∵∠BOD=∠AOC(对顶角相等),∠AOC=60°( )
∴∠ = °
∵OE平分∠BOD( 已知 )
∴∠BOE=∠ = °( )
∵OF⊥OE( 已知 )
∴∠EOF= °( )
∵∠BOF+∠BOE=∠EOF
∴∠BOF= °.
28.如图,直线、相交于点,平分,.
(1)求的度数;
(2)若,是否平分?
29.如图,直线与相交于点.
(1)若,求,的度数;
(2)若,求,的度数(用含的式子表示).
30.点O是直线AB上的一点,射线OC从OA出发绕点O顺时针方向旋转,旋转到OB停止,设(),射线,作射线OE平分.
(1)如图1,若,且OD在直线AB的上方,求的度数(要求写出简单的几何推理过程).
(2)射线OC顺时针旋转一定的角度得到图2,当射线OD在直线AB的下方时,其他条件不变,请你用含的代数式表示的度数,(要求写出简单的几何推理过程).
(3)射线OC从OA出发绕点O顺时针方向旋转到OB,在旋转过程中你发现与()之间有怎样的数量关系?请你直接用含的代数式表示的度数.
答案
一、单选题
1.B
【分析】根据对顶角的定义作出判断即可.
【解析】解:根据对顶角的定义可知:只有第三个图中的两个角是对顶角,其它都不是.
故选:B.
2.D
【分析】依据邻补角的定义进行判断即可.
【解析】解:.两个角不存在公共边,故不是邻补角,故不符合题意;
、两个角不存在公共边,故不是邻补角,故不符合题意;
、两个角不存在公共边,故不是邻补角,故不符合题意;
、两个角是邻补角,故符合题意.
故选:D.
3.C
【分析】根据邻补角定义、对顶角定义和性质逐项判断解答即可.
【解析】A.有一条边是公共边,另一边互为反向延长线的两个角是邻补角,故A不符合题意.
B.对顶角指角的两边互为反向的延长线的两个角,相等的角不一定是对顶角,故B不符合题意.
C.根据对顶角的性质,对顶角一定相等,故C符合题意.
D.例如等腰三角形的底角不是对顶角,但两个底角相等,故D不符合题意.
故选:C.
4.C
【分析】本题考查了角平分线的定义及对顶角相等等知识点.先根据角平分线的定义得出,再根据对顶角相等即可得出答案.
【解析】解:∵平分,
∴,
∴.
故选:C.
5.A
【分析】根据对顶角和邻补角的定义逐项判断即可.
【解析】解:A、和是邻补角,当减小时,增加,故选项正确,符合题意;
B、和是对顶角,当减小时,也减小,故选项错误,不符合题意;
C、和是邻补角,当减小时,增加,故选项错误,不符合题意;
D、和都与是邻补角,当减小时,和都增加,与的和增大,故选项错误,不符合题意;
故选:A.
6.C
【解析】解:(1)连接直线外一点与直线上各点的所有线段中,垂线段最短,故此选项正确;
∵在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,经过的点不确定,可以画无数条,
故(2)(3)选项正确;
∵从直线外一点到这条直线的垂线段的长叫做点到直线的距离,故(4)选项错误;
∴正确的选项是(1)(2)(3),共3个,
故选:C.
7.B
【分析】根据对顶角的性质:对顶角相等,邻补角的性质:邻补角互补,进行求解即可.
【解析】解:∵∠1与∠2是对顶角,
∴∠1=∠2,
∵∠1与∠3是邻补角,
∴∠1+∠3=180°,
∴∠2+∠3=180°.
故选B.
8.B
【分析】设∠EOB=x度,∠EOC=2x度,把角用未知数表示出来,建立x的方程,用代数方法解几何问题是一种常用的方法.
【解析】解:设∠EOB=x,则∠EOC=2x,
则∠BOD=(180°-3x),
则∠BOE+∠BOD=∠DOE,
即x+(180°-3x)=72°,
解得x=36°,
故∠EOC=2x=72°.
故选B.
9.C
【分析】设,根据题意得出,,则,根据平分线的定义得出,然后逐项分析判断即可求解.
【解析】解:设,∵OE平分,
∴,
∴,则,
∵OG平分,OF平分,
∴
∴,故①正确;
∵,∵未知,
故②不正确;
,故③正确;
,故④正确,
故选:C.
10.C
【分析】由题目所给信息进行分析后找出规律,归纳为一般性公式即可得到答案.
【解析】由题目所给信息进行分析总结可得,
n条直线最多交点个数M= ,
当n=8时,=28,
故选C.
二、填空题
11.
【分析】本题主要考查了点到直线的距离,根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,进行判断即可,熟练掌握点到直线的距离是解此题的关键.
【解析】解:,
线段的长是点到直线的距离,
故答案为:.
12.
【分析】此题主要考查了垂线段最短,正确理解题意是解题关键.直接利用跳远成绩应该是垂线段最短距离进而得出答案.
【解析】解:由题意可得:小涛同学这次跳远的成绩应该是的长米.
故答案为:.
13. / 和
【分析】对顶角:有公共顶点且两条边都互为反向延长线的两个角称为对顶角.邻补角的定义:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,叫做邻补角.根据这两个定义求解即可.
【解析】解:的对顶角是;
的邻补角是,;
故答案为:;,.
14. 或
【分析】根据对顶角定义,结合图形可知的对顶角是;根据邻补角定义,结合图形可知的邻补角是或,从而得到答案.
【解析】解:由图可知,的对顶角是;的邻补角是或,
故答案为:;或.
15.25
【分析】本题考查与角平分线有关的计算.先求出的度数,进而求出的度数,利用,进行计算即可.正确的识图,找准线段之间的和差关系,是解题的关键.
【解析】解:∵,
∴,,
∵是的平分线,
∴,
∴;
故答案为:25.
16.
【分析】首先根据平分,可得,再根据,计算出和的度数,然后计算出的度数,再根据角平分线的定义可得.
【解析】解:∵平分,
∴,
∵,,
∴,,
∴,
∵平分,
∴.
故答案为:
17. 2 、 /38度
【分析】根据对顶角的定义及性质、邻补角的定义及性质分析解答即可.
【解析】解:(1)图中的对顶角有和;和;共2对,
故答案为:2;
(2)的邻补角是、,
故答案为:、;
(3)∵,
∴,
∵,
∴,
故答案为:.
18.
【分析】由垂直可知,,再利用已知条件,得出,进而求得,即可求出的度数.
【解析】解:,
,
,,
,
,
,
,
,
,
,
故答案为:.
三、解答题
19.(1)如图,线段即为点A到的垂线段,
(2)如图,线段即为所作的垂线,
20.(1)的邻补角为的邻补角为
(2)与互为对顶角,与互为对顶角
21.(1)∵,
∴点到直线的距离是线段的长;
故答案为:.
(2)∵,
∴点到直线的距离是线段的长;
故答案为:.
(3)∵,
∴线段的长表示点到直线距离;
故答案为: .
(4)∵,
∴线段的长表示点到直线距离;
故答案为:.
(5)∵,
∴线段的长表示点到直线距离;
故答案为:,.
(6)∵,
∴线段的长表示点到直线距离;
故答案为:,.
22.(1)解:的对顶角是,
∵,
∴的邻补角是,
故答案为:,.
(2)解:∵,平分,
∴,
∴,
∵,
∴,
∴的度数为.
23.(1)解:如图,直线PE即为所求;
(2)解:如图,直线PF即为所求;
(3)解:点O到直线PE的距离是线段OP的长.
故答案为:OP;
(4)解:由图可知,点P到直线CD的距离为0,
故答案为:0.
24.解:(1)如图:AD即为所求
(2)如图: BE即为所求
(3)因为BC//AD,所以三角形ABC的高为4cm;
所以;
故答案为4
25.解:射线平分,
,
由于,可设,则,
又,
,
,
,
解得,
,
答:的度数为
26.解:(1)
(2)因为OA平分,,
所以.
又因为,
所以.
(3)因为,,
所以,.
由(2)可得.
27.解:∵∠BOD=∠AOC(对顶角相等),∠AOC=60°(已知),
∴∠BOD=60°,
∵OE平分∠BOD(已知),
∴∠BOE=∠BOD=30°(角平分线的定义),
∵OF⊥OE(已知),
∴∠EOF=90°(垂直定义),
∵∠BOF+∠BOE=∠EOF,
∴∠BOF=60°.
故答案为:已知;BOD;60;BOD;30;角平分线的定义;90;垂直定义;60.
28.(1)解:解:∵,
∴,
又∵平分,
∴;
(2)解:平分,理由为:
∵,
∴,
∴,
∴,
∴,
∴平分.
29.(1)∵,,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
(2)根据对顶角相等有:,,
∵,,
∴,,
∴.
30.(1)解:∵OD⊥OC,
∴∠COD=90°,
∵,即,
∴,
∵OE平分∠BOD,
∴.
(2),
,
∵OD⊥OC,
∴∠COD=90°,
∴
∵OE平分∠BOD,
∴.
(3)①当,OD在直线AB的上方时,如图所示:
,
∵OE平分∠BOD,
∴,
即.
②当,OD在直线AB的下方时,如图所示:
∵,
∴,
∵OE平分∠BOD,
∴,
即.
③当,OD在直线AB的上方时,如图所示:
,
,
∵OE平分∠BOD,
∴,
即.
④当,OD在直线AB的下方时,如图所示:
∵,
,
∵OE平分∠BOD,
∴,
即.
综上分析可知,即或即或即或即.
一、单选题
1.下面四个图形中,与是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
2.下列图形中,∠1与∠2互为邻补角的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.互补的两个角是邻补角 B.相等的角必是对顶角
C.对顶角一定相等 D.若两个角不是对顶角,则这两个角不相等
4.如图,已知直线与相交于点F,平分,若,则度数是( )
A. B. C. D.
5.如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型,固定木条a,转动木条b,当减小时,下列说法正确的是( )
A.增大 B.增大 C.减小 D.与的和增大
6.下列说法中正确的个数有( )
(1)直线外一点与直线上各点连接的所有线段中,垂线段最短.
(2)画一条直线的垂线段可以画无数条.
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离.
A.1个 B.2个 C.3个 D.4个
7.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3的度数为( )
A.90° B.180° C.270° D.360°
8.如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=∠COE,∠DOE=72°.则∠COE的度数是( )
A.36° B.72° C.44° D.56°
9.如图,为直线上一点,,OE平分,OG平分,OF平分,下列结论:①;②与互补;③;④,其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
10.如图,2条直线 最多有=1个交点,3条直线最多有=3个交点,4条直线最多有=6个交点,……由此猜想,8条直线最多有___个交点.
A.32 B.16 C.28 D.40
二、填空题
11.点在直线上,,垂足为,,则线段的长是点到直线 的距离.
12.如图,这是小涛同学在体育课上某一次跳远后留下的脚印.通过测量得到如下数据:米,米,米,米,其中AC,DE分别垂直起跳线于C,E.小涛这次跳远成绩是 米.
13.如图,直线相交于点O,则的对顶角是 ,的邻补角是 .
14.如图,直线相交于点.的对顶角是 ,的邻补角是 .
15.如图,点O是直线上一点,,是的平分线,则的度数是 °.
16.如图,直线、相交于点O,平分,平分,且,则的度数为 .
17.如图,直线相交于点O,.
(1)图中的对顶角有 对;
(2)的邻补角是 ;
(3)如果,,那么 .
18.如图,已知直线,作,垂足为,在内部,在内部,且,,则的度数为 .
三、解答题
19.如图所示,是钝角.(不写作图过程,保留作图痕迹)
(1)画出点A到的垂线段.
(2)过点C画的垂线.
20.如图,直线相交于点是内部的一条射线.
(1)写出和的邻补角;
(2)写出图中所有的对顶角.
21.如图,已知于,于.
(1)点到直线的距离是线段_______的长;
(2)点到直线的距离是线段_______的长;
(3)线段的长表示点到直线_______距离;
(4)线段的长表示点到直线_______距离;
(5)线段的长表示点_______到直线______距离;
(6)线段的长表示点_______到直线______距离;
22.如图,直线和直线相交于点,平分.
(1)写出图中的对顶角______,和两个邻补角______;
(2)若,求的度数.
23.按下列要求画图并填空:如图,直线AB与CD相交于点O,P是CD上的一点.
(1)过点P画出CD的垂线,交直线AB于点E;
(2)过点P画PF⊥AB,垂足为点F;
(3)点O到直线PE的距离是线段 的长;
(4)点P到直线CD的距离为 .
24.按下列要求画图并填空:如图,
(1)过点A画直线BC的平行线AD;
(2)过点B画直线AD的垂线段,垂足为点E;
(3)若点B到直线AD的距离为4,BC=2,则= .
25.如图,直线与相交于点,,,射线平分,求的度数.
26.如图,直线AB,CD相交于点O,OA平分.
(1)的对顶角为________;
(2)若,求的度数;
(3)若,求的度数.
27.如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.
解:∵∠BOD=∠AOC(对顶角相等),∠AOC=60°( )
∴∠ = °
∵OE平分∠BOD( 已知 )
∴∠BOE=∠ = °( )
∵OF⊥OE( 已知 )
∴∠EOF= °( )
∵∠BOF+∠BOE=∠EOF
∴∠BOF= °.
28.如图,直线、相交于点,平分,.
(1)求的度数;
(2)若,是否平分?
29.如图,直线与相交于点.
(1)若,求,的度数;
(2)若,求,的度数(用含的式子表示).
30.点O是直线AB上的一点,射线OC从OA出发绕点O顺时针方向旋转,旋转到OB停止,设(),射线,作射线OE平分.
(1)如图1,若,且OD在直线AB的上方,求的度数(要求写出简单的几何推理过程).
(2)射线OC顺时针旋转一定的角度得到图2,当射线OD在直线AB的下方时,其他条件不变,请你用含的代数式表示的度数,(要求写出简单的几何推理过程).
(3)射线OC从OA出发绕点O顺时针方向旋转到OB,在旋转过程中你发现与()之间有怎样的数量关系?请你直接用含的代数式表示的度数.
答案
一、单选题
1.B
【分析】根据对顶角的定义作出判断即可.
【解析】解:根据对顶角的定义可知:只有第三个图中的两个角是对顶角,其它都不是.
故选:B.
2.D
【分析】依据邻补角的定义进行判断即可.
【解析】解:.两个角不存在公共边,故不是邻补角,故不符合题意;
、两个角不存在公共边,故不是邻补角,故不符合题意;
、两个角不存在公共边,故不是邻补角,故不符合题意;
、两个角是邻补角,故符合题意.
故选:D.
3.C
【分析】根据邻补角定义、对顶角定义和性质逐项判断解答即可.
【解析】A.有一条边是公共边,另一边互为反向延长线的两个角是邻补角,故A不符合题意.
B.对顶角指角的两边互为反向的延长线的两个角,相等的角不一定是对顶角,故B不符合题意.
C.根据对顶角的性质,对顶角一定相等,故C符合题意.
D.例如等腰三角形的底角不是对顶角,但两个底角相等,故D不符合题意.
故选:C.
4.C
【分析】本题考查了角平分线的定义及对顶角相等等知识点.先根据角平分线的定义得出,再根据对顶角相等即可得出答案.
【解析】解:∵平分,
∴,
∴.
故选:C.
5.A
【分析】根据对顶角和邻补角的定义逐项判断即可.
【解析】解:A、和是邻补角,当减小时,增加,故选项正确,符合题意;
B、和是对顶角,当减小时,也减小,故选项错误,不符合题意;
C、和是邻补角,当减小时,增加,故选项错误,不符合题意;
D、和都与是邻补角,当减小时,和都增加,与的和增大,故选项错误,不符合题意;
故选:A.
6.C
【解析】解:(1)连接直线外一点与直线上各点的所有线段中,垂线段最短,故此选项正确;
∵在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,经过的点不确定,可以画无数条,
故(2)(3)选项正确;
∵从直线外一点到这条直线的垂线段的长叫做点到直线的距离,故(4)选项错误;
∴正确的选项是(1)(2)(3),共3个,
故选:C.
7.B
【分析】根据对顶角的性质:对顶角相等,邻补角的性质:邻补角互补,进行求解即可.
【解析】解:∵∠1与∠2是对顶角,
∴∠1=∠2,
∵∠1与∠3是邻补角,
∴∠1+∠3=180°,
∴∠2+∠3=180°.
故选B.
8.B
【分析】设∠EOB=x度,∠EOC=2x度,把角用未知数表示出来,建立x的方程,用代数方法解几何问题是一种常用的方法.
【解析】解:设∠EOB=x,则∠EOC=2x,
则∠BOD=(180°-3x),
则∠BOE+∠BOD=∠DOE,
即x+(180°-3x)=72°,
解得x=36°,
故∠EOC=2x=72°.
故选B.
9.C
【分析】设,根据题意得出,,则,根据平分线的定义得出,然后逐项分析判断即可求解.
【解析】解:设,∵OE平分,
∴,
∴,则,
∵OG平分,OF平分,
∴
∴,故①正确;
∵,∵未知,
故②不正确;
,故③正确;
,故④正确,
故选:C.
10.C
【分析】由题目所给信息进行分析后找出规律,归纳为一般性公式即可得到答案.
【解析】由题目所给信息进行分析总结可得,
n条直线最多交点个数M= ,
当n=8时,=28,
故选C.
二、填空题
11.
【分析】本题主要考查了点到直线的距离,根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,进行判断即可,熟练掌握点到直线的距离是解此题的关键.
【解析】解:,
线段的长是点到直线的距离,
故答案为:.
12.
【分析】此题主要考查了垂线段最短,正确理解题意是解题关键.直接利用跳远成绩应该是垂线段最短距离进而得出答案.
【解析】解:由题意可得:小涛同学这次跳远的成绩应该是的长米.
故答案为:.
13. / 和
【分析】对顶角:有公共顶点且两条边都互为反向延长线的两个角称为对顶角.邻补角的定义:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,叫做邻补角.根据这两个定义求解即可.
【解析】解:的对顶角是;
的邻补角是,;
故答案为:;,.
14. 或
【分析】根据对顶角定义,结合图形可知的对顶角是;根据邻补角定义,结合图形可知的邻补角是或,从而得到答案.
【解析】解:由图可知,的对顶角是;的邻补角是或,
故答案为:;或.
15.25
【分析】本题考查与角平分线有关的计算.先求出的度数,进而求出的度数,利用,进行计算即可.正确的识图,找准线段之间的和差关系,是解题的关键.
【解析】解:∵,
∴,,
∵是的平分线,
∴,
∴;
故答案为:25.
16.
【分析】首先根据平分,可得,再根据,计算出和的度数,然后计算出的度数,再根据角平分线的定义可得.
【解析】解:∵平分,
∴,
∵,,
∴,,
∴,
∵平分,
∴.
故答案为:
17. 2 、 /38度
【分析】根据对顶角的定义及性质、邻补角的定义及性质分析解答即可.
【解析】解:(1)图中的对顶角有和;和;共2对,
故答案为:2;
(2)的邻补角是、,
故答案为:、;
(3)∵,
∴,
∵,
∴,
故答案为:.
18.
【分析】由垂直可知,,再利用已知条件,得出,进而求得,即可求出的度数.
【解析】解:,
,
,,
,
,
,
,
,
,
,
故答案为:.
三、解答题
19.(1)如图,线段即为点A到的垂线段,
(2)如图,线段即为所作的垂线,
20.(1)的邻补角为的邻补角为
(2)与互为对顶角,与互为对顶角
21.(1)∵,
∴点到直线的距离是线段的长;
故答案为:.
(2)∵,
∴点到直线的距离是线段的长;
故答案为:.
(3)∵,
∴线段的长表示点到直线距离;
故答案为: .
(4)∵,
∴线段的长表示点到直线距离;
故答案为:.
(5)∵,
∴线段的长表示点到直线距离;
故答案为:,.
(6)∵,
∴线段的长表示点到直线距离;
故答案为:,.
22.(1)解:的对顶角是,
∵,
∴的邻补角是,
故答案为:,.
(2)解:∵,平分,
∴,
∴,
∵,
∴,
∴的度数为.
23.(1)解:如图,直线PE即为所求;
(2)解:如图,直线PF即为所求;
(3)解:点O到直线PE的距离是线段OP的长.
故答案为:OP;
(4)解:由图可知,点P到直线CD的距离为0,
故答案为:0.
24.解:(1)如图:AD即为所求
(2)如图: BE即为所求
(3)因为BC//AD,所以三角形ABC的高为4cm;
所以;
故答案为4
25.解:射线平分,
,
由于,可设,则,
又,
,
,
,
解得,
,
答:的度数为
26.解:(1)
(2)因为OA平分,,
所以.
又因为,
所以.
(3)因为,,
所以,.
由(2)可得.
27.解:∵∠BOD=∠AOC(对顶角相等),∠AOC=60°(已知),
∴∠BOD=60°,
∵OE平分∠BOD(已知),
∴∠BOE=∠BOD=30°(角平分线的定义),
∵OF⊥OE(已知),
∴∠EOF=90°(垂直定义),
∵∠BOF+∠BOE=∠EOF,
∴∠BOF=60°.
故答案为:已知;BOD;60;BOD;30;角平分线的定义;90;垂直定义;60.
28.(1)解:解:∵,
∴,
又∵平分,
∴;
(2)解:平分,理由为:
∵,
∴,
∴,
∴,
∴,
∴平分.
29.(1)∵,,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
(2)根据对顶角相等有:,,
∵,,
∴,,
∴.
30.(1)解:∵OD⊥OC,
∴∠COD=90°,
∵,即,
∴,
∵OE平分∠BOD,
∴.
(2),
,
∵OD⊥OC,
∴∠COD=90°,
∴
∵OE平分∠BOD,
∴.
(3)①当,OD在直线AB的上方时,如图所示:
,
∵OE平分∠BOD,
∴,
即.
②当,OD在直线AB的下方时,如图所示:
∵,
∴,
∵OE平分∠BOD,
∴,
即.
③当,OD在直线AB的上方时,如图所示:
,
,
∵OE平分∠BOD,
∴,
即.
④当,OD在直线AB的下方时,如图所示:
∵,
,
∵OE平分∠BOD,
∴,
即.
综上分析可知,即或即或即或即.
同课章节目录
