湖北省北大附中武汉为明实验学校人教版七年级数学下册课件:6.1 平方根(共20张PPT)
文档属性
| 名称 | 湖北省北大附中武汉为明实验学校人教版七年级数学下册课件:6.1 平方根(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 213.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-29 00:00:00 | ||
图片预览







文档简介
课件20张PPT。6.1 平方根第六章 实 数情境引入合作探究课堂小结课后作业第3课时 平方根首页1.什么叫做算术平方根?2.判断下列各数有没有算术平方根,如果有请求出它们的算术平方根。
100;1; ; 0; -0.0025; (-3)2 ; -25; 首页3.什么叫乘方?什么叫幂? 答:求相同因数的积的运算叫做乘方;乘方的运算结果叫做幂。(1)32= ,(-3)2= ;(2) , ;(3)(0.8)2= ,(-0.8)2= 。90.640.644. 填空9首页显然 乘方是已知底数和指数,求幂。如: 32已知底数3及指数2,求幂9。 反过来:如果已知一个数平方等于9,怎样求这个数?
即知已指数2及幂9,求底数?首页如果一个数的平方等于9,这个数是多少?由于 ,
所以这个数是3或-3.首页根据上面的研究过程填表:如果我们把 分别叫做
的平方根,你能类比算术平方根的概念,
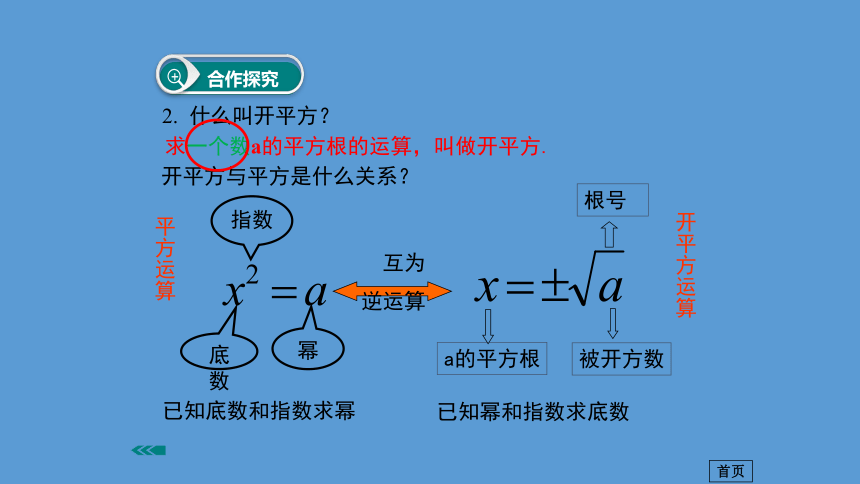
给出平方根的概念吗?首页 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 x2=a ,那么x 叫做a的平方根.因为3 、-3的平方都等于9,我们把3及-3叫做9的平方根。1、什么叫平方根首页2. 什么叫开平方? 求一个数a的平方根的运算,叫做开平方.开平方与平方是什么关系?a的平方根底数幂被开方数 互为
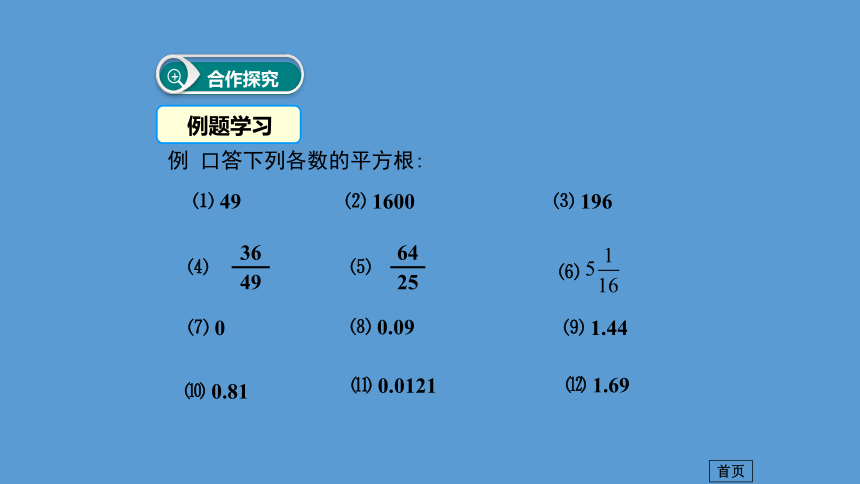
逆运算指数根号已知底数和指数求幂已知幂和指数求底数平方运算开平方运算首页例 口答下列各数的平方根: ⑴ 49 ⑵ 1600 ⑶ 196 ⑺ 0 ⑻ 0.09 ⑼ 1.44 ⑽ 0.81 ⑾ 0.0121 ⑿ 1.69 ⑹ 首页例2 判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是±8;
(5)-16的平方根是-4.首页1、4的平方根是什么?
2、0 的平方根是多少?
3、-4有没有平方根?为什么? 4、正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
从以上你发现平方根有什么特点?首页(1)正数的平方根有两个,它们互为相反数;
(2)0的平方根就是0 ;(3)负数没有平方根.平方根的性质首页表示a的正的平方根表示a 的负的平方根记作说一说各表示什么意义?表示7的正的平方根表示7的负的平方根表示7的平方根a﹙ a≥0 ﹚的平方根表示为一个非负数的平方根的表示方法:算术平方根首页2根指数被开方数读作:
二次根号m简写为:
读作:
根号m(m≥0)根号首页解(1)(2) 例3 求下列各式的值:(1)(2)(3) (3)首页例4 判断下列各式计算是否正确,并说明理由.首页例5 求下列各式的值:解:(1) ; (2) ; (3) .合作探究首页平方根与算术平方根的联系与区别:联系 (1)具有包含关系:平方根包含算术平方根,算术平方根是平方根的一种。(2) 存在条件相同:平方根和算术平方根都具有非负性
(3) 0的平方根和算术平方根都是0。区别(1) 定义不同: “如果一个数X的平方等于a,那么这个数x叫做a的平方根”,
“如果一个正数x的平方等于a,即 x2 =a,那么这个正数x叫做a的算术平方根”。
(2)个数不同:一个正数有两个平方根,而一个正数的算术平方根只有一个;
(3)表示方法不同:正数a的算术平方根表示为 ,而正数a的平方根表示为±课堂小结首页1、平方根(二次方根)和开平方的定义
2、平方根的性质
3、平方根的表示方法:正数a的平方根可以
用符号“ ”表示读作“正、负根号a”
4、被开方数的取值范围:符号“ ”
只有a≥0时有意义, a≤0时无意义。
5、平方根与算术平方根的联系与区别。见《新观察》本课作业首页
100;1; ; 0; -0.0025; (-3)2 ; -25; 首页3.什么叫乘方?什么叫幂? 答:求相同因数的积的运算叫做乘方;乘方的运算结果叫做幂。(1)32= ,(-3)2= ;(2) , ;(3)(0.8)2= ,(-0.8)2= 。90.640.644. 填空9首页显然 乘方是已知底数和指数,求幂。如: 32已知底数3及指数2,求幂9。 反过来:如果已知一个数平方等于9,怎样求这个数?
即知已指数2及幂9,求底数?首页如果一个数的平方等于9,这个数是多少?由于 ,
所以这个数是3或-3.首页根据上面的研究过程填表:如果我们把 分别叫做
的平方根,你能类比算术平方根的概念,
给出平方根的概念吗?首页 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 x2=a ,那么x 叫做a的平方根.因为3 、-3的平方都等于9,我们把3及-3叫做9的平方根。1、什么叫平方根首页2. 什么叫开平方? 求一个数a的平方根的运算,叫做开平方.开平方与平方是什么关系?a的平方根底数幂被开方数 互为
逆运算指数根号已知底数和指数求幂已知幂和指数求底数平方运算开平方运算首页例 口答下列各数的平方根: ⑴ 49 ⑵ 1600 ⑶ 196 ⑺ 0 ⑻ 0.09 ⑼ 1.44 ⑽ 0.81 ⑾ 0.0121 ⑿ 1.69 ⑹ 首页例2 判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是±8;
(5)-16的平方根是-4.首页1、4的平方根是什么?
2、0 的平方根是多少?
3、-4有没有平方根?为什么? 4、正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
从以上你发现平方根有什么特点?首页(1)正数的平方根有两个,它们互为相反数;
(2)0的平方根就是0 ;(3)负数没有平方根.平方根的性质首页表示a的正的平方根表示a 的负的平方根记作说一说各表示什么意义?表示7的正的平方根表示7的负的平方根表示7的平方根a﹙ a≥0 ﹚的平方根表示为一个非负数的平方根的表示方法:算术平方根首页2根指数被开方数读作:
二次根号m简写为:
读作:
根号m(m≥0)根号首页解(1)(2) 例3 求下列各式的值:(1)(2)(3) (3)首页例4 判断下列各式计算是否正确,并说明理由.首页例5 求下列各式的值:解:(1) ; (2) ; (3) .合作探究首页平方根与算术平方根的联系与区别:联系 (1)具有包含关系:平方根包含算术平方根,算术平方根是平方根的一种。(2) 存在条件相同:平方根和算术平方根都具有非负性
(3) 0的平方根和算术平方根都是0。区别(1) 定义不同: “如果一个数X的平方等于a,那么这个数x叫做a的平方根”,
“如果一个正数x的平方等于a,即 x2 =a,那么这个正数x叫做a的算术平方根”。
(2)个数不同:一个正数有两个平方根,而一个正数的算术平方根只有一个;
(3)表示方法不同:正数a的算术平方根表示为 ,而正数a的平方根表示为±课堂小结首页1、平方根(二次方根)和开平方的定义
2、平方根的性质
3、平方根的表示方法:正数a的平方根可以
用符号“ ”表示读作“正、负根号a”
4、被开方数的取值范围:符号“ ”
只有a≥0时有意义, a≤0时无意义。
5、平方根与算术平方根的联系与区别。见《新观察》本课作业首页
