初中数学沪教版(五四学制)八年级下册 12.4 平面向量及其加减运算 (含解析)
文档属性
| 名称 | 初中数学沪教版(五四学制)八年级下册 12.4 平面向量及其加减运算 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 646.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览




文档简介
第四节 平面向量及其加减运算
一、单选题
1.下列判断中,不正确的是( )
A. B.
C.如果,那么 D.
2.如果点、在线段上,,那么下列结论中正确的是( )
A.与是相等向量 B.与是相等向量
C.与是相反向量 D.与是平行向量
3.如图,四边形是平行四边形,下列说法正确的是( )
A.与是相等向量 B.与是相等向量
C.与是相反向量 D.与是平行向量
4.如图,点在平行四边形的边上,,下列结论中正确的是( )
A.与是相等的向量 B.与是相等的向量
C.与互为相反向量 D.与是平行向量
5.分别以正方形的四个顶点为起点与终点的所有有向线段能表示的不同向量有( )
A.个 B.个 C.个 D.个
6.式子化简结果是( )
A. B. C. D.
7.如图,在矩形ABCD中,=
A. B.
C. D.
8.已知四边形是矩形,点是对角线与的交点.下列四种说法:①向量与向量是相等的向量;②向量与向量是互为相反的向量;③向量与向量是相等的向量;④向量与向量是平行向量.其中正确的个数为( )
A.1 B.2 C.3 D.4
9.如图,在正六边形中,等于( )
A. B. C. D.
10.下列命题中,真命题的个数为( )
①方向相同 ②方向相反
③有相等的模 ④方向相同
A.0 B.1 C.2 D.3
二、填空题
11.计算: .
12.在菱形中,已知,,那么 (结果用向量,的式子表示).
13.在□ABCD中,O是对角线的交点,那么 .
14.化简:()-()= .
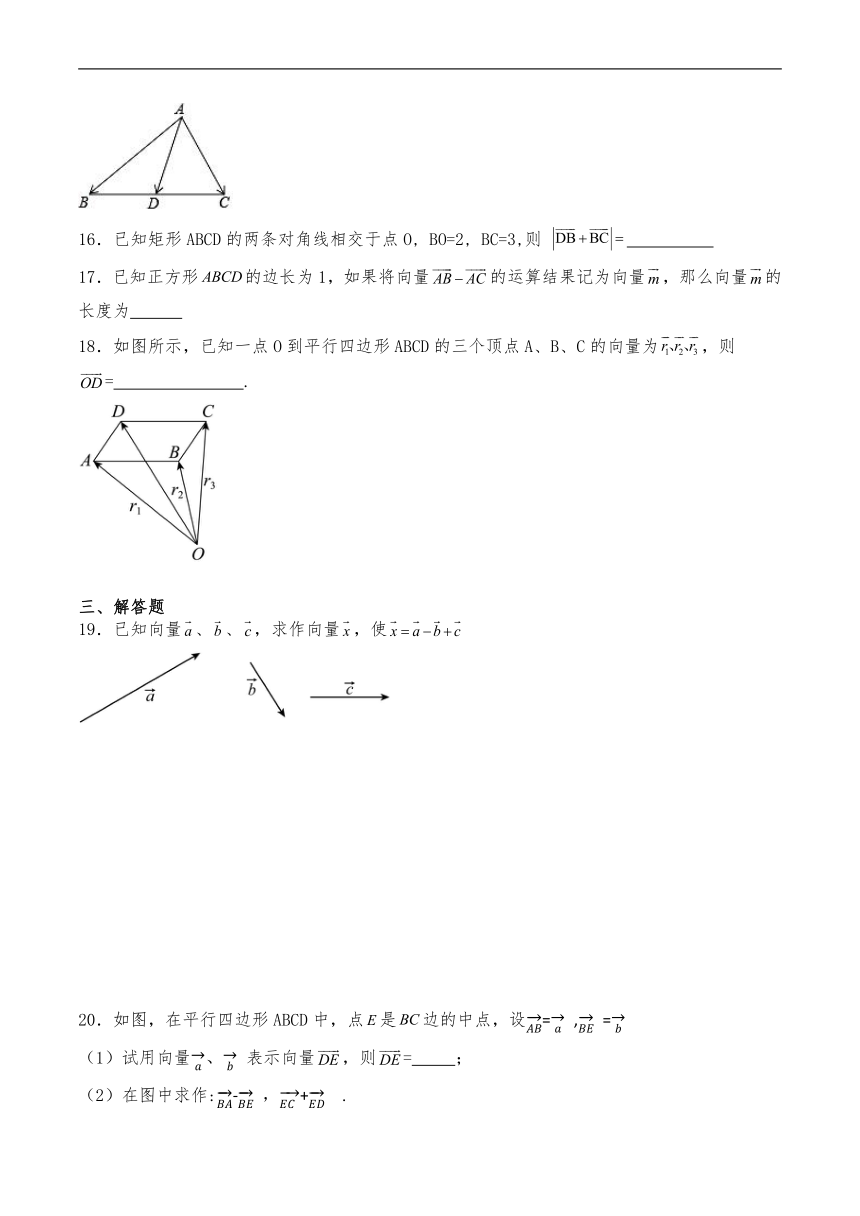
15.如图,在△ABC中,AD是边BC上的中线,设向量=,=,如果用向量,表示向量,那么向量可以表示为 .
16.已知矩形ABCD的两条对角线相交于点O, BO=2, BC=3,则
17.已知正方形的边长为1,如果将向量的运算结果记为向量,那么向量的长度为
18.如图所示,已知一点O到平行四边形ABCD的三个顶点A、B、C的向量为,则= .
三、解答题
19.已知向量、、,求作向量,使
20.如图,在平行四边形ABCD中,点是边的中点,设= , =
(1)试用向量、 表示向量,则= ;
(2)在图中求作:- ,+ .
(保留作图痕迹,不要求写作法,但要写出结果)
21.如图,在 ABCD中,对角线AC与BD相交于点O,设,.
(1)试用向量,表示下列向量:= ;= ;
(2)求作:.(保留作图痕迹,写出结果,不要求写作法).
22.如图,、、分别为等边三角形的边、、的中点,在以、、、、、为起点或终点的向量中,求出与平行的向量.
23.如图,在ABCD中,AB∥CD,AD=BC,∠B=60°,AC平分∠DAB.
(1)求∠ACB的度数;
(2)如果AD=1,请直接写出向量和向量的模.
24.如图,已知:在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF
(1)在图中画出向量的差向量并填空: .
(2)图中与平行的向量是 .
(3)若,用 表示=
25.材料一,在平面里有两点,,若为起点,为终点,则把有方向且有长度的线段叫做向量,记为:,并且可用坐标表示这个向量,表示方法为:
,向量的长度可以表示成
例如:,则,
即所以
材料二:若,,则
若时,则⊥ .
根据材料解决下列问题:
已知中,,,
(1)=________ ___________
(2)当时,求证:是直角三角形.
(3)若,,求使恒成立的的取值范围.
答案
一、单选题
1.C
【分析】根据向量是既有方向又有大小的量,向量的加法满足所有的加法运算定律,逐项进行分析判断即可.
【解析】解:A.,故A正确,不符合题意;
B.,故B正确,不符合题意;
C.如果,那么或,故C错误,符合题意;
D.,故D正确,不符合题意.
故选:C.
2.D
【解析】解:点、在线段上,,
.
A、与方向相反,,故本选项错误;
B、与方向相反,,故本选项错误;
C、相反向量是方向相反,模相等的两向量,而,与不是相反向量,故本选项错误;
D、与共线,与是平行向量,故本选项正确.
故选:.
由点、在线段上,,可得,然后根据相等向量、相反向量与平行向量的定义,即可求得答案.注意排除法的应用.
3.B
【解析】解:四边形是平行四边形,
,,
与是等向量.
故选:.
根据等向量的定义判断即可.
4.D
【解析】解:、与是相等的向量,错误它们方向不同,本选项不符合题意.
B、与是相等的向量,错误它们方向不同,本选项不符合题意.
C、与互为相反向量,错误数量不相等,本选项不符合题意.
D、与是平行向量,本选项符合题意.
故选:.
根据相等向量,平行向量的定义一一判断即可.
5.C
【解析】本题考查了相等向量的定义,向量的几何意义,考查了计算能力,属于基础题.本题考查了相等向量的定义,向量的几何意义,考查了计算能力,属于基础题.
可画出图形,然后写出以正方形的四个顶点为起点与终点的所有有向线段能表示的不同向量,然后即可得出正确的选项.
解:如图,以正方形的四个顶点为起点与终点的所有有向线段能表示的不同向量为:
,共个.
故选:
6.B
【解析】根据向量的线性运算法则,准确化简,即可求解.
由
.
故选:B.
7.B
【解析】由题意,
故选B.
8.C
【分析】利用矩形的性质,相等向量,平行向量的定义一一判断即可.
【解析】解:如图:
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,OA=OC,OB=OD,
∴①向量与向量是相等的向量,正确.
②向量与向量是互为相反的向量,正确.
③向量与向量是相等的向量;错误.
④向量与向量是平行向量.正确.
故选:C.
9.A
【解析】根据相等向量和向量加法运算直接计算即可.
,.
故选:A.
10.C
【分析】直接利用向量共线的基本性质逐一核对四个命题得答案.
【解析】解:对于①,若,则方向相同,①正确;
对于②,若,则方向相反,②正确;
对于③,若,则方向相反,但的模不一定,③错误;
对于④,若,则能推出的方向相同,但的方向相同,得到④错误.
所以正确命题的个数是2个,故选:C.
二、填空题
11.
【分析】根据平面向量的加减法计算即可.
【解析】解:
=,
=,
故答案为:.
12.
【分析】根据菱形的性质可知,,然后利用即可得出答案.
【解析】∵四边形是菱形,
∴,
∵,,
∴
∴
故答案为:.
13.
【分析】由向量的平行四边形法则及相等向量的概念可得答案.
【解析】解:因为:□ABCD,
所以,,
所以:.
故答案为:.
14..
【解析】由去括号的法则可得:=,然后由加法的交换律与结合律可得:,继而求得答案.
解:====.
故答案为.
15.+
【分析】如图,延长AD到E,使得DE=AD,连接BE,CE.证明四边形ABEC是平行四边形,利用三角形法则求出即可解决问题.
【解析】解:如图,延长AD到E,使得DE=AD,连接BE,CE.
∵AD=DE,BD=CD,
∴四边形ABEC是平行四边形,
∴,
∵,
∴.
故答案为:+.
16.
【分析】首先利用矩形的性质和勾股定理求出CD的长度,然后根据即可得出结果.
【解析】解:在矩形ABCD中,BO=2, BC=3,
∴BD=4,
∴,
∴=,
故答案为.
17.1
【分析】利用向量的三角形法则直接求得答案.
【解析】如图:
∵-==且||=1,
∴||=1.
故答案为1.
18.
【分析】利用向量的线性运算,结合平行四边形的性质,即可求得结论.
【解析】解:∵如图:
∴.
三、解答题
19.如图所示,即为所求.
20.解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是BC的中点,
∴BE=EC,
∵,,.
∴;
(2)如图:
,,
向量,向量即为所求.
21.解:(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD,OA=OC,
∴===﹣,
==﹣﹣.
故答案为:﹣,﹣﹣.
(2)如图,延长BC到E,使得CE=BC,则即为所求.
22.解:∵、分别为等边三角形的边、的中点,
∴EF∥BC
∴与平行的向量有、、、、、.
23.(1)∵CD∥AB,AD=BC,
∴四边形ABCD是等腰梯形,
∴∠DAB=∠B=60°,
∵AC平分∠DAB,
∴∠CAB=∠DAB=30°,
∴∠B+∠CAB=90°,
∴∠ACB=90°.
(2)∵CD∥AB,
∴∠DCA=∠CAB=∠CAD=30°,
∴AD=CD=BC=1,
在Rt△ABC中,∵∠CAB=30°,∠ACB=90°,
∴AB=2BC=2,
∵,
∴向量和向量的模分别为1和2.
24.解:(1),
画出向量的差如图:
(2)连接AC交BD于点O,
在平行四边形ABCD中,OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
∴AE∥CF,
∴与平行的向量是:,,
故答案为,;
(3)∵,
∴,即.
故答案为.
25.(1)∵A( 3,3),B(8,4),
∴AB=(8 ( 3),4 3),即AB=(11,1),
|AB|=
故答案为:(11,1);
(2)当x=2时,A( 3,3),B(8,4),C(2, 2)
此时AB2=( 3 8)2+(4 3)2=122,
AC2=( 3 2)2+[3 ( 2)]2=50,BC2=(2 8)2+( 2 4)2=72.
得AB2=AC2+BC2
∴△ABC是直角三角形.
(3)∵A( 3,3),B(8,4),C(x, x)
∴AB=(11,1),AC=(x+3, x 3),BC=(x 8, x 4)
∴a=AB AC=11x+33 x 3=10x+30
b=AC BC=x2 5x 24+x2+7x+12=2x2+2x 12
∴a+b=10x+30+2x2+2x 12=2x2+12x+18
∴由a+b>m 2得到:2x2+12x+18>m 2
即:m<2x2+12x+20
∴m<2(x+3)2+2
∵2(x+3)2+2 2.
∴m<2
∴使a+b>m 2恒成立的m的取值范围是:m<2
故答案为:m<2
一、单选题
1.下列判断中,不正确的是( )
A. B.
C.如果,那么 D.
2.如果点、在线段上,,那么下列结论中正确的是( )
A.与是相等向量 B.与是相等向量
C.与是相反向量 D.与是平行向量
3.如图,四边形是平行四边形,下列说法正确的是( )
A.与是相等向量 B.与是相等向量
C.与是相反向量 D.与是平行向量
4.如图,点在平行四边形的边上,,下列结论中正确的是( )
A.与是相等的向量 B.与是相等的向量
C.与互为相反向量 D.与是平行向量
5.分别以正方形的四个顶点为起点与终点的所有有向线段能表示的不同向量有( )
A.个 B.个 C.个 D.个
6.式子化简结果是( )
A. B. C. D.
7.如图,在矩形ABCD中,=
A. B.
C. D.
8.已知四边形是矩形,点是对角线与的交点.下列四种说法:①向量与向量是相等的向量;②向量与向量是互为相反的向量;③向量与向量是相等的向量;④向量与向量是平行向量.其中正确的个数为( )
A.1 B.2 C.3 D.4
9.如图,在正六边形中,等于( )
A. B. C. D.
10.下列命题中,真命题的个数为( )
①方向相同 ②方向相反
③有相等的模 ④方向相同
A.0 B.1 C.2 D.3
二、填空题
11.计算: .
12.在菱形中,已知,,那么 (结果用向量,的式子表示).
13.在□ABCD中,O是对角线的交点,那么 .
14.化简:()-()= .
15.如图,在△ABC中,AD是边BC上的中线,设向量=,=,如果用向量,表示向量,那么向量可以表示为 .
16.已知矩形ABCD的两条对角线相交于点O, BO=2, BC=3,则
17.已知正方形的边长为1,如果将向量的运算结果记为向量,那么向量的长度为
18.如图所示,已知一点O到平行四边形ABCD的三个顶点A、B、C的向量为,则= .
三、解答题
19.已知向量、、,求作向量,使
20.如图,在平行四边形ABCD中,点是边的中点,设= , =
(1)试用向量、 表示向量,则= ;
(2)在图中求作:- ,+ .
(保留作图痕迹,不要求写作法,但要写出结果)
21.如图,在 ABCD中,对角线AC与BD相交于点O,设,.
(1)试用向量,表示下列向量:= ;= ;
(2)求作:.(保留作图痕迹,写出结果,不要求写作法).
22.如图,、、分别为等边三角形的边、、的中点,在以、、、、、为起点或终点的向量中,求出与平行的向量.
23.如图,在ABCD中,AB∥CD,AD=BC,∠B=60°,AC平分∠DAB.
(1)求∠ACB的度数;
(2)如果AD=1,请直接写出向量和向量的模.
24.如图,已知:在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF
(1)在图中画出向量的差向量并填空: .
(2)图中与平行的向量是 .
(3)若,用 表示=
25.材料一,在平面里有两点,,若为起点,为终点,则把有方向且有长度的线段叫做向量,记为:,并且可用坐标表示这个向量,表示方法为:
,向量的长度可以表示成
例如:,则,
即所以
材料二:若,,则
若时,则⊥ .
根据材料解决下列问题:
已知中,,,
(1)=________ ___________
(2)当时,求证:是直角三角形.
(3)若,,求使恒成立的的取值范围.
答案
一、单选题
1.C
【分析】根据向量是既有方向又有大小的量,向量的加法满足所有的加法运算定律,逐项进行分析判断即可.
【解析】解:A.,故A正确,不符合题意;
B.,故B正确,不符合题意;
C.如果,那么或,故C错误,符合题意;
D.,故D正确,不符合题意.
故选:C.
2.D
【解析】解:点、在线段上,,
.
A、与方向相反,,故本选项错误;
B、与方向相反,,故本选项错误;
C、相反向量是方向相反,模相等的两向量,而,与不是相反向量,故本选项错误;
D、与共线,与是平行向量,故本选项正确.
故选:.
由点、在线段上,,可得,然后根据相等向量、相反向量与平行向量的定义,即可求得答案.注意排除法的应用.
3.B
【解析】解:四边形是平行四边形,
,,
与是等向量.
故选:.
根据等向量的定义判断即可.
4.D
【解析】解:、与是相等的向量,错误它们方向不同,本选项不符合题意.
B、与是相等的向量,错误它们方向不同,本选项不符合题意.
C、与互为相反向量,错误数量不相等,本选项不符合题意.
D、与是平行向量,本选项符合题意.
故选:.
根据相等向量,平行向量的定义一一判断即可.
5.C
【解析】本题考查了相等向量的定义,向量的几何意义,考查了计算能力,属于基础题.本题考查了相等向量的定义,向量的几何意义,考查了计算能力,属于基础题.
可画出图形,然后写出以正方形的四个顶点为起点与终点的所有有向线段能表示的不同向量,然后即可得出正确的选项.
解:如图,以正方形的四个顶点为起点与终点的所有有向线段能表示的不同向量为:
,共个.
故选:
6.B
【解析】根据向量的线性运算法则,准确化简,即可求解.
由
.
故选:B.
7.B
【解析】由题意,
故选B.
8.C
【分析】利用矩形的性质,相等向量,平行向量的定义一一判断即可.
【解析】解:如图:
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,OA=OC,OB=OD,
∴①向量与向量是相等的向量,正确.
②向量与向量是互为相反的向量,正确.
③向量与向量是相等的向量;错误.
④向量与向量是平行向量.正确.
故选:C.
9.A
【解析】根据相等向量和向量加法运算直接计算即可.
,.
故选:A.
10.C
【分析】直接利用向量共线的基本性质逐一核对四个命题得答案.
【解析】解:对于①,若,则方向相同,①正确;
对于②,若,则方向相反,②正确;
对于③,若,则方向相反,但的模不一定,③错误;
对于④,若,则能推出的方向相同,但的方向相同,得到④错误.
所以正确命题的个数是2个,故选:C.
二、填空题
11.
【分析】根据平面向量的加减法计算即可.
【解析】解:
=,
=,
故答案为:.
12.
【分析】根据菱形的性质可知,,然后利用即可得出答案.
【解析】∵四边形是菱形,
∴,
∵,,
∴
∴
故答案为:.
13.
【分析】由向量的平行四边形法则及相等向量的概念可得答案.
【解析】解:因为:□ABCD,
所以,,
所以:.
故答案为:.
14..
【解析】由去括号的法则可得:=,然后由加法的交换律与结合律可得:,继而求得答案.
解:====.
故答案为.
15.+
【分析】如图,延长AD到E,使得DE=AD,连接BE,CE.证明四边形ABEC是平行四边形,利用三角形法则求出即可解决问题.
【解析】解:如图,延长AD到E,使得DE=AD,连接BE,CE.
∵AD=DE,BD=CD,
∴四边形ABEC是平行四边形,
∴,
∵,
∴.
故答案为:+.
16.
【分析】首先利用矩形的性质和勾股定理求出CD的长度,然后根据即可得出结果.
【解析】解:在矩形ABCD中,BO=2, BC=3,
∴BD=4,
∴,
∴=,
故答案为.
17.1
【分析】利用向量的三角形法则直接求得答案.
【解析】如图:
∵-==且||=1,
∴||=1.
故答案为1.
18.
【分析】利用向量的线性运算,结合平行四边形的性质,即可求得结论.
【解析】解:∵如图:
∴.
三、解答题
19.如图所示,即为所求.
20.解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是BC的中点,
∴BE=EC,
∵,,.
∴;
(2)如图:
,,
向量,向量即为所求.
21.解:(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD,OA=OC,
∴===﹣,
==﹣﹣.
故答案为:﹣,﹣﹣.
(2)如图,延长BC到E,使得CE=BC,则即为所求.
22.解:∵、分别为等边三角形的边、的中点,
∴EF∥BC
∴与平行的向量有、、、、、.
23.(1)∵CD∥AB,AD=BC,
∴四边形ABCD是等腰梯形,
∴∠DAB=∠B=60°,
∵AC平分∠DAB,
∴∠CAB=∠DAB=30°,
∴∠B+∠CAB=90°,
∴∠ACB=90°.
(2)∵CD∥AB,
∴∠DCA=∠CAB=∠CAD=30°,
∴AD=CD=BC=1,
在Rt△ABC中,∵∠CAB=30°,∠ACB=90°,
∴AB=2BC=2,
∵,
∴向量和向量的模分别为1和2.
24.解:(1),
画出向量的差如图:
(2)连接AC交BD于点O,
在平行四边形ABCD中,OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
∴AE∥CF,
∴与平行的向量是:,,
故答案为,;
(3)∵,
∴,即.
故答案为.
25.(1)∵A( 3,3),B(8,4),
∴AB=(8 ( 3),4 3),即AB=(11,1),
|AB|=
故答案为:(11,1);
(2)当x=2时,A( 3,3),B(8,4),C(2, 2)
此时AB2=( 3 8)2+(4 3)2=122,
AC2=( 3 2)2+[3 ( 2)]2=50,BC2=(2 8)2+( 2 4)2=72.
得AB2=AC2+BC2
∴△ABC是直角三角形.
(3)∵A( 3,3),B(8,4),C(x, x)
∴AB=(11,1),AC=(x+3, x 3),BC=(x 8, x 4)
∴a=AB AC=11x+33 x 3=10x+30
b=AC BC=x2 5x 24+x2+7x+12=2x2+2x 12
∴a+b=10x+30+2x2+2x 12=2x2+12x+18
∴由a+b>m 2得到:2x2+12x+18>m 2
即:m<2x2+12x+20
∴m<2(x+3)2+2
∵2(x+3)2+2 2.
∴m<2
∴使a+b>m 2恒成立的m的取值范围是:m<2
故答案为:m<2
