22.3 特殊的平行四边形 同步练习(含解析)2024-2025学年八年级下册沪教版(五四学制)(2024)
文档属性
| 名称 | 22.3 特殊的平行四边形 同步练习(含解析)2024-2025学年八年级下册沪教版(五四学制)(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览



文档简介
22.3 特殊的平行四边形
一、单选题
1.正方形具有而矩形不一定具有的性质是( )
A.四个角相等 B.对角线互相垂直
C.对角互补 D.对角线相等
2.如图,在菱形中,对角线,相交于点,若,则的度数为( )
A. B. C. D.
3.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )
A. B. C.9 D.12
4.下面说法正确的是( )
A.有一组邻边相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.矩形的对角线相等 D.对角线互相垂直平分的四边形是正方形
5.如图,正方形的对角线相交于点O,则的度数是( )
A. B. C. D.
6.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
A.5cm B.6cm C.cm D.cm;
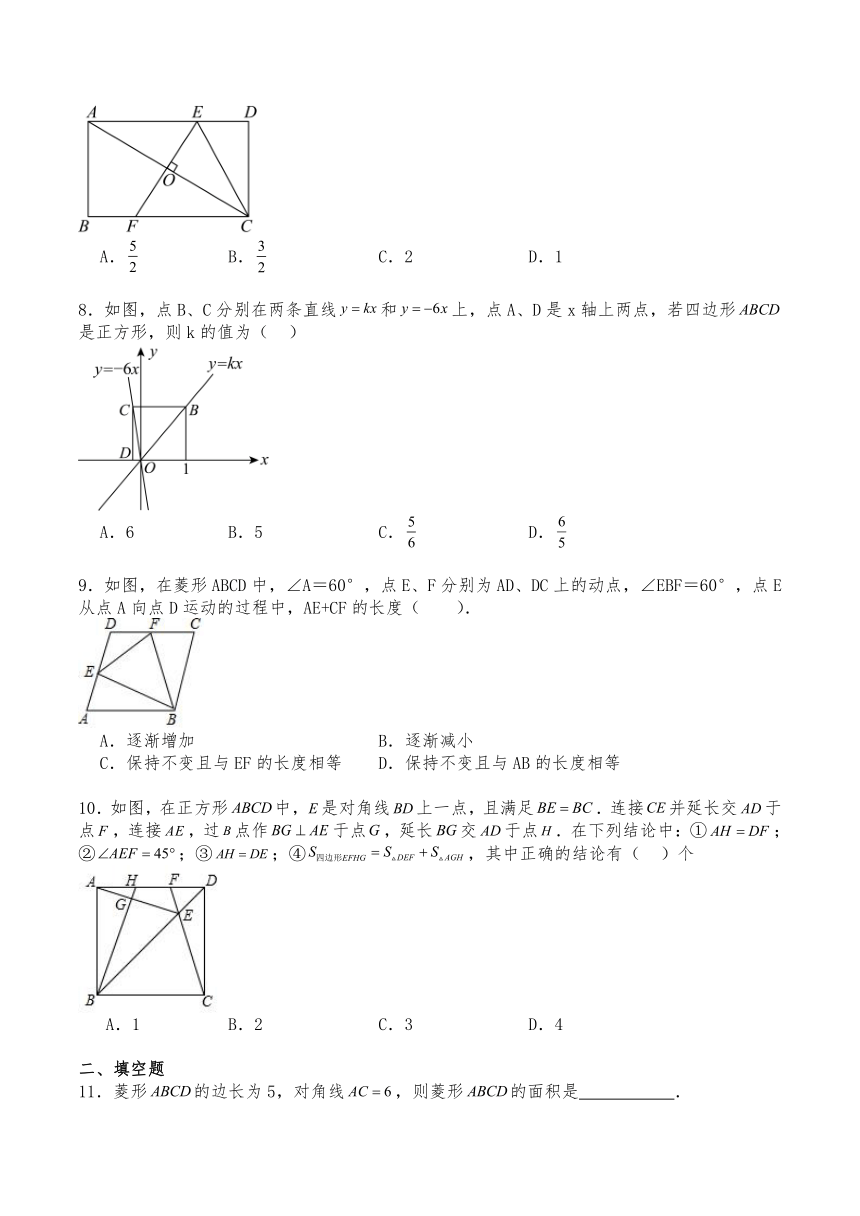
7.如图,矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则△DCE的面积为( )
A. B. C.2 D.1
8.如图,点B、C分别在两条直线和上,点A、D是x轴上两点,若四边形是正方形,则k的值为( )
A.6 B.5 C. D.
9.如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( ).
A.逐渐增加 B.逐渐减小
C.保持不变且与EF的长度相等 D.保持不变且与AB的长度相等
10.如图,在正方形中,是对角线上一点,且满足.连接并延长交于点,连接,过点作于点,延长交于点.在下列结论中:①;②;③;④,其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
11.菱形的边长为5,对角线,则菱形的面积是 .
12.要使矩形ABCD成为正方形,可添加的条件是 (写一个即可).
13.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E=
14.如图,一张长,宽的矩形纸片,将它沿某直线折叠使得A、C重合,则折痕的长为 .
15.如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF= .
16.已知,矩形,点在边上,点在边上,连接、交于点.若,,,.则 .
17.如图,在平面直角坐标系中,四边形是边长为1的正方形,顶点分别在轴的正半轴上.点Q在对角线上,且,连接并延长交边于点P,则点P的坐标为 .
18.如图,有一张矩形纸片,已知,,现将纸片进行如下操作:现将纸片沿折痕进行折叠,使点落在边上的点处,点在上(如图),则 ;然后将绕点旋转到,当过点时旋转停止,则的长度为 .
三、解答题
19.如图,矩形的对角线,相交于点,过点作的平行线交的延长线于点.
(1)求证:.
(2)若,,求的长.
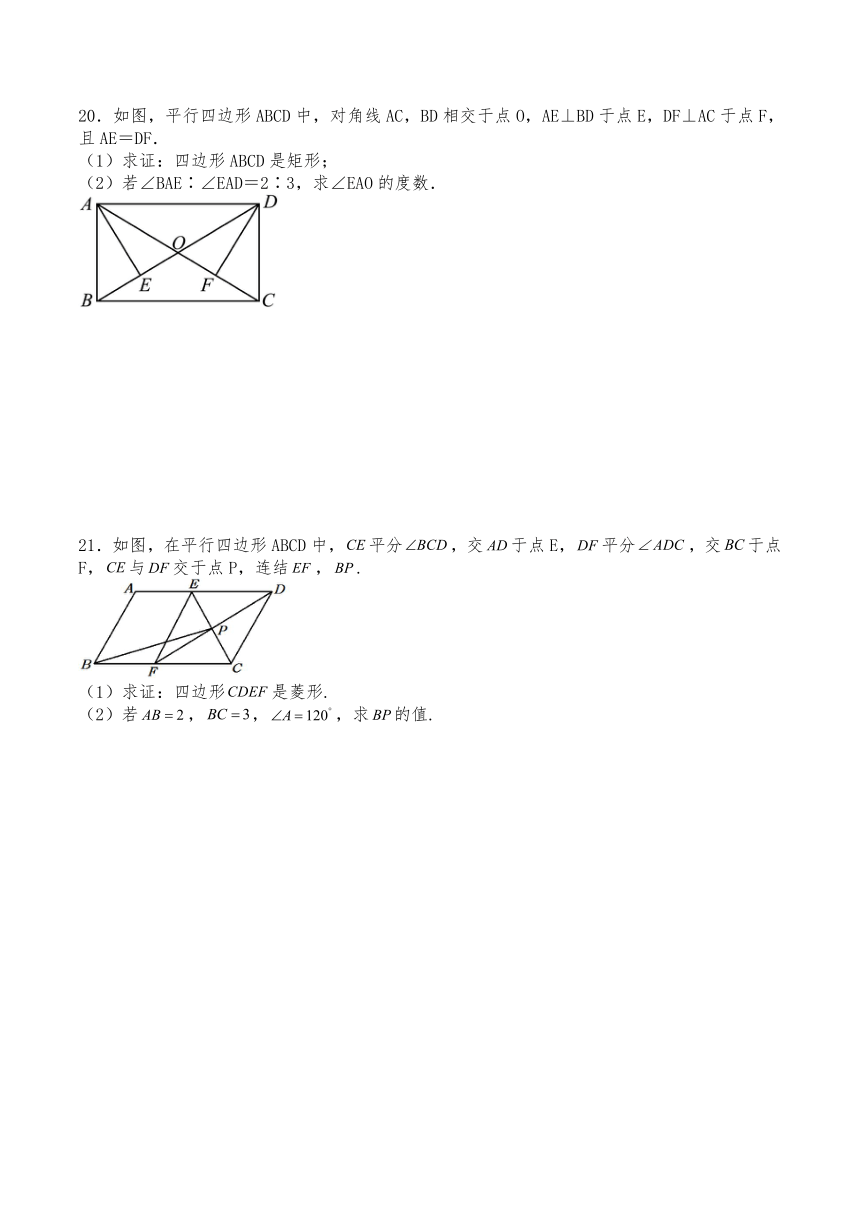
20.如图,平行四边形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F,且AE=DF.
(1)求证:四边形ABCD是矩形;
(2)若∠BAE∶∠EAD=2∶3,求∠EAO的度数.
21.如图,在平行四边形ABCD中,平分,交于点E,平分,交于点F,与交于点P,连结,.
(1)求证:四边形是菱形.
(2)若,,,求的值.
22.如图,在6×6的方格纸中,请按要求作图.
(1)图1中,A,B是方格纸中的格点,以AB为一边作一个矩形ABCD,要求C,D两点也在格点上;
(2)图2中,E,F是方格纸中的格点,以EF为一边作一个菱形EFGH,要求G,H两点也在格点上.
23.已知:如图,在正方形ABCD中,BD为对角线,E、F分别是AD,CD上的点,且AE=CF,连接BE、BF、EF.
(1)求证:EM=FM;
(2)若DE:AE=2:1,设S△ABE=S,求S△BEF(用含S的代数式表示).
24.在正方形ABCD中,AC是对角线,点E在AD边上(不与点A重合),点F在CD边上,连接BE,BF,EF,已知∠DEF=45°.
(1)求证:BE=BF.
(2)设AE=k AD(0<k<1),△ABE的面积为S1,△DEF的面积为S2.
①当k=时,求证:S1=2S2;
②当S2=2S1时,求k的值.
25.如图,在矩形中,,.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是.连接、、.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形是矩形,请说明理由;
(2)当t为何值时,四边形是菱形,请说明理由;
(3)直接写出(2)中菱形的周长和面积,周长是______cm,面积是______.
26.如图,在平行四边形ABCD中,,E,F分别为,的中点,作于点G,的延长线交的延长线于点H.
(1)求证:四边形是菱形.
(2)当时,
①求的长.
②如图2,交于点P,记的面积为,的面积为,则的值为________.
27.如图,在平面直角坐标系中,点A(0,8),点B是x轴的正半轴上的一个动点,连接AB,取AB的中点M,将线段MB绕着点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0)
(1)当t=6时,点M的坐标是______;
(2)求点C的坐标(用含t的代数式表示);
(3)是否存在点B,使四边形AOBD为矩形?若存在,请求出点B的坐标;若不存在,请说明理由;
(4)在点B的运动过程中,平面内是否存在一点N,使得以A、B、N、D为顶点的四边形是菱形?若存在,请直接写出点N的纵坐标(不必要写横坐标);若不存在,请说明理由.
28.正方形中,边长为,点在对角线上,连接,过点作,交直线于点.
(1)如图,当点在边上时,求证:;
(2)当点在的延长线上时,设,面积为,求关于的解析式,并写出定义域;
(3)若,求BM的长.
答案
一、单选题
1.B
【分析】本题考查了正方形和矩形的性质,解决本题的关键是熟记正方形和矩形的性质.对于四边形的性质我们从:①边;②角;③对角线三个方面去理解,因此,只需要根据正方形、矩形的这三个方面性质的不同,即可解答.
【解析】解:根据正方形和矩形的性质对比分析:
①边:有对边与邻边:正方形与矩形对边性质相同,没有区别;邻边性质不同,正方形邻边相等,矩形邻边不相等;
②角:正方形与矩形内角性质相同,对角相等、邻角互补、四个角都是直角;
③对角线:正方形与矩形对角线都相等且互相平分,但正方形对角线相互垂直,而矩形对角线不具有这个特征;
故选:B.
2.B
【分析】根据菱形的性质得到,,再进一步求解即可.
【解析】解:四边形是菱形,
,,
,
,
,
故选B.
3.B
【分析】根据矩形对角线相等且互相平分的性质和题中的条件易得△AOB为等边三角形,即可得到矩形对角线的长,进而求解即可.
【解析】
如图:AB=6,∠AOB=60°,
∵四边形是矩形,AC,BD是对角线,
∴OA=OB=OC=OD=BD=AC,
在△AOB中,OA=OB,∠AOB=60°,
∴OA=OB=AB=6,BD=2OB=12,
∴BC=.
故选:B.
4.C
【分析】根据菱形,矩形,正方形的性质和判定定理,逐个进行判断即可.
【解析】解:A、有一组邻边相等的平行四边形是菱形,故A不正确,不符合题意;
B、对角线互相垂直的平行四边形是菱形,故B不正确,不符合题意;
C、矩形的对角线相等,故C正确,符合题意;
D、对角线相等且互相垂直平分的四边形是正方形,故D不正确,不符合题意;
故选:C.
5.D
【分析】直接利用正方形的性质求解即可.
【解析】解:∵四边形是正方形,
∴,
∴,
故选:D.
6.D
【分析】首先利用菱形的性质结合勾股定理得出BC的长,再利用三角形面积求出答案
【解析】解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC==5(cm),
∵S△ABC=AE×BC=BO×AC
故5AE=24,
解得:AE=(cm).
故选D.
7.B
【分析】由EF垂直平分AC可得AE=CE,设CE=x,则ED=AD﹣AE=4﹣x,在Rt△CDE中,利用勾股定理求出x的长,继而根据三角形的面积公式进行求解即可.
【解析】∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=4,∠D=90°,
∵EO是AC的垂直平分线,
∴AE=CE,
设CE=x,则ED=AD﹣AE=4﹣x,
在Rt△CDE中,CE2=CD2+ED2,
即x2=22+(4﹣x)2,
解得:x=,
即CE的长为,
DE=4﹣=,
所以△DCE的面积=××2=,
故选B.
8.D
【分析】设点,根据正方形的性质可得,再代入求得,再根据,,列方程求解即可.
【解析】解:∵点B、C分别在两条直线和上,
设点,
∵四边形是正方形,
∴,
∴把代入得,,
∴,
∴,,
∴,
∴,
故选:D.
9.D
【分析】证明△ABE≌△DBF(AAS),可得AE=DF;结合图形可知:AE+CF=AB,AB是一定值,从而完成求解.
【解析】连接BD
∵四边形ABCD是菱形,
∴AB=AD=CD,
∵∠A=60°
∴△ABD是等边三角形
∴AB=BD,∠ABD=60°
∵DC∥AB
∴∠CDB=∠ABD=60°
∴∠A=∠CDB
∵∠EBF=60°
∴∠ABE+∠EBD=∠EBD+∠DBF
∴∠ABE=∠DBF
∵
∴△ABE≌△DBF(AAS)
∴AE=DF
∴AE+CF=DF+CF=CD=AB
故选:D.
10.C
【分析】先判断出∠DAE=∠ABH,再判断△ADE≌△CDE得出∠DAE=∠DCE=22.5°,∠ABH=∠DCF,再判断出△ABH≌△DCF从而得到①正确,根据三角形的外角求出∠AEF=45°,得出②正确;结合①②可得DF=DE,根据AH=DF即可得③正确;连接HE,判断出S△EFH≠S△EFD得出④错误.
【解析】解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在△ABH和△DCF中,
,
∴△ABH≌△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故①②正确;
∵∠FDE=45°,∠DFE=∠FAE+∠AEF=22.5°+45°=67.5°,
∴∠DEF=180°﹣45°﹣67.5°=67.5°,
∴DF=DE,
∵AH=DF,
∴AH=DE,故③正确;
如图,连接HE,
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故④错误,
∴正确的是①②③.
故选:C
二、填空题
11.24
【分析】根据菱形的对角线互相垂直,再利用勾股定理求出另一条对角线的长度,根据菱形的面积计算方法求解即可.
【解析】如图所示,
∵菱形的边长为5,
∴,,
又∵,
∴,
∴,
∴,
∴菱形的面积.
故答案为:24.
12.AB=BC;BC=CD;CD=AD;AD=AB;AC⊥BD(挑选一个即可)
【分析】根据正方形的判定定理进行添加即可.
【解析】从边上添加:有AB=BC,BC=CD,CD=DA,DA=AB(有一组领边相等的矩形为正方形)
从对角线上添加:有AC⊥BD(对角线互相垂直的矩形为正方形).
故答案为:AB=BC;BC=CD;CD=AD;AD=AB;AC⊥BD(挑选一个即可)
13.22.5 °
【分析】由于正方形的对角线平分一组对角,那么∠ACB=45°,即∠ACE=135°,在等腰△CAE中,已知了顶角的度数,即可由三角形内角和定理求得∠E的度数.
【解析】解:正方形对角线平分直角,故∠ACD=45°,
已知DC⊥CE,则∠ACE=∠135°,
又∵CE=AC,
∴∠E==22.5°.
故答案为:22.5°.
14.
【分析】由题意可知,连接,利用翻折的性质可知,,,进而可得,则,设,则,在中由勾股定理可得,列出方程即可求得,在中由勾股定理可得,进而可求得折痕的长度.
【解析】解:由题意可知,,,,
∴,
连接,
由翻折可知,,,,则,
∵,
∴,
∴,
∴,
设,则,
在中由勾股定理可得:,
即:,解得:,即:,
∴在中由勾股定理可得:,
∴.
故答案为:.
15.
【分析】连接OP.由勾股定理得出AC=10,可求得OA=OB=5,由矩形的性质得出S矩形ABCD=AB BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,由S△AOB=S△AOP+S△BOP=OA PE+OB PF=OA(PE+PF)=×5×(PE+PF)=12求得答案.
【解析】解:连接OP,如图:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC,OB=OD,AC=BD,
∴OA=OB,AC==10,
∴S矩形ABCD=AB BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,
∴S△AOB=S△AOP+S△BOP=OA PE+OB PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF=;
故答案为:.
16.6
【分析】过点作,垂足为,交于点H,证明,得出是等腰直角三角形,进而得出四边形是平行四边形,即可求解.
【解析】解:如图所示,过点作,垂足为,交于点H,
∵四边形是矩形,
∴,
∴,
∵,,,
∴,
∴
∴,,
∴是等腰直角三角形,
∴,
∵,
∴,
又∵,
∴四边形是平行四边形,
∴,
∴,
故答案为:6.
17.
【分析】首先根据正方形的性质得到对角线,结合题意推出,并由正方形的性质推出∠BPQ=∠BQP,得到,从而得到,即可得出结论.
【解析】解:∵四边形OABC是边长为1的正方形,
∴根据勾股定理,得对角线,
∵OQ=OC,
∴,∠OCQ=∠OQC,
∵OC//AB,
∴∠OCQ=∠BPQ,
∵∠OQC=∠BQP(对顶角相等),
∴∠BPQ=∠BQP,
∴,
∴,
又 ∵OA=1,
∴点P的坐标为,
故答案为:.
18. 2
【分析】连接,证四边形是正方形,得,进而得,,由勾股定理得,证明()得,,从而点垂直平分,点垂直平分,,最后利用面积公式构造方程即可得解.
【解析】解:∵四边形是矩形,
∴,,,
∵将纸片沿折痕进行折叠,使点落在边上的点处,点在上,
∴,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,
∴,,
∴,
连接,
∵将绕点旋转到,
∴,,
∵,
∴()
∴,,
∴点垂直平分,点垂直平分,
∴,
∴,即,
∴,
故答案为:,.
三、解答题
19.(1)证明:四边形是矩形,
,,
.
,
四边形是平行四边形,
,
.
(2)解:四边形是矩形,
,,
.
∴
,
,
.
20.(1)解:∵,
∴
又∵,
∴△AEO≌△DFO
∴
∵四边形是平行四边形
∴
∴
∴四边形是矩形
(2)解:∵ ,是矩形
∴,
∴在中,
∴在中,
∴在中,
21.(1)∵在平行四边形ABCD中,平分,
∴∠BCE=∠DCE,∠BCE=∠DEC,
∴∠DCE=∠DEC,
∴DE=DC,
∵平分,
∴∠ADF=∠CDF,∠ADF=∠DFC,
∴∠CDF =∠DFC,
∴CF=DC=DE,
∵ED∥FC,
∴四边形是菱形;
(2)作PH⊥BC于点H,
∵∠BAD=120°,
∴∠PCH=60°,
∵四边形是菱形,AB=2,
∴CE=2,
∴CP=1,
∴CH=,PH=,
∵BC=3,
∴BH=,
∴.
22.解:(1)如图1,四边形ABCD即为所求作的矩形;
(2)如图2,四边形EFGH即为所求作的菱形;
.
23.(1)∵四边形ABCD是正方形,
∴,
又∵AE=CF,
∴,
∴是等腰三角形,
又∵,
∴EM=FM;
(2)∵DE:AE=2:1,
∴设,,,
∴,
∴,
同理可求得:,
∴,
∴.
24.(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠BCD=∠D=90°,AB=BC=CD=AD,
在Rt△DEF中,∠DEF=45°,
∴∠DFE=90°-∠DEF=45°=∠DEF,
∴DE=DF,
∴AD- DE=CD -DF,
∴AE=CF,
∴△ABE≌△CBF(SAS),
∴BE=BF;
(2)解:设AD=x,则AB=AD=x,
∵AE=k AD,
∴AE=k x,
∴DE=DF=AD- AE=x -kx=(1-k)x,
∴S1=AE AB=k x x=kx2,
S2=DE DF= [(1-k)x]2=(1-k)2x2,
①当k=时,S1=kx2=x2,
S2=(1-k)2x2=(1-)2x2=x2,
∴S1=2S2;
②当S2=2S1时,2×kx2=(1-k)2x2,
∴k=2+(由于0<k<1,所以,舍去)或k=2-,
即k=2-.
25.(1)解:由题意得,,则,
四边形是矩形,
,,
当时,四边形为矩形,
,
解得,,
故当时,四边形为矩形;
(2)解:由(1)可知,四边形为平行四边形,
当时,四边形为菱形,
即时,四边形为菱形,
解得,,
故当时,四边形为菱形;
(3)解:当时,,
菱形的周长为:,
菱形的面积为:,
故答案为:15;.
26.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E、F分别为BC、AD中点,
∴AF=AD,BE=BC,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AD=2AB,AD=2AF,
∴AB=AF,
∴四边形ABEF是菱形;
(2)①连接AE交BF于点O,
∵四边形ABEF是菱形,
∴AE⊥BF,OB=OF=BE=4,OA=OE=AE,
∴∠AOB=90°,
在Rt△AOB中,OA==3,
∴AE=2OA=6,
∴S菱形ABEF=AE·BF=×6×8=24,
∵E、F分别是BC、AD中点,
∴BE=EC,AF=FD,
∵AD∥BC,
∴四边形ABEF,四边形EFDC都是平行四边形,且底和高相等,
∴S四边形ABEF=S四边形EFDC=24,
∴S四边形ABCD=S四边形ABEF+S四边形EFDC=48,
∵CG⊥AB,
∴S四边形ABEF=AB·CG=5CG=48,∠BGC=90°,
∴CG=,
∵AD=BC=2AB=10,
∴BG=,
∴AG=AB -BG=5-=,
∵四边形ABCD是平行四边形,
∴AB=CD=5,AB∥CD,
∴∠A=∠FDH,∠GCH=∠BGC=90°,
∵F是AD中点,
∴AF=DF,
在△AFG和△DFH中,
,
∴△AFG≌△DFH(ASA),
∴AG=DH=,
∴CH=CD+DH=5+=,
在Rt△GCH中,GH==12;
②过F作FK⊥AB交BA延长线于K,
∴S四边形ABEF=AB·FK=5FK=24,
∴FK=,
∴S△BGF=BG·FK==,
S△BGC=BG·CG==,
∵S2=S△BGC -S△BGP=-S△BGP,
S1=S△BGF -S△BGP=-S△BGP,
∴S2-S1=-=.
27.(1)如图1中,
,,,
,
故答案为:(3,4);
(2)如图1中,作于,轴于.
∵,
,,
,
,,
,
,
,
,,
,
.
(3)存在.
如图2中,作于,轴于.
理由:由题意当时,
,
四边形是平行四边形,
,
四边形是矩形,
,
四边形是矩形,
又∵由(2)得,
即:,解得:.
.
(4)①如图3中,当时,以为对角线可得菱形,此时点在轴上.作BE⊥AC交于点E,
设,,
∵点M是AB的中点,,
∴,
∵,,,
∴,
∴,
∴,
在中,则有,
①②联立,解得:,
,
点的纵坐标为3.
②如图4中,当时,以为对角线可得菱形.此时点的纵坐标为8.
③,
不存在以为对角线的菱形.
综上所述,满足条件的点的纵坐标为3或8.
28.(1)过点作于点,于点,
,
四边形是正方形,
,,
,
,
,
,
,
,
,
;
(2)过点作于点,交于点.
,
在正方形中,,,
四边形为矩形,
,,,
,
,
,
,
在中,,,
,
,
,
又,,
,
,
,
,
,
,
;
(3)当点在边上时,连接,交于,过作于,
在正方形中,,,
,
在中,,则,
∵S BNM= BM NE,,且,
,
∵∠AOB=900,
,
,
,
又,
,
,
,
当点在的延长线上时,同理可得.
一、单选题
1.正方形具有而矩形不一定具有的性质是( )
A.四个角相等 B.对角线互相垂直
C.对角互补 D.对角线相等
2.如图,在菱形中,对角线,相交于点,若,则的度数为( )
A. B. C. D.
3.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )
A. B. C.9 D.12
4.下面说法正确的是( )
A.有一组邻边相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.矩形的对角线相等 D.对角线互相垂直平分的四边形是正方形
5.如图,正方形的对角线相交于点O,则的度数是( )
A. B. C. D.
6.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
A.5cm B.6cm C.cm D.cm;
7.如图,矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则△DCE的面积为( )
A. B. C.2 D.1
8.如图,点B、C分别在两条直线和上,点A、D是x轴上两点,若四边形是正方形,则k的值为( )
A.6 B.5 C. D.
9.如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( ).
A.逐渐增加 B.逐渐减小
C.保持不变且与EF的长度相等 D.保持不变且与AB的长度相等
10.如图,在正方形中,是对角线上一点,且满足.连接并延长交于点,连接,过点作于点,延长交于点.在下列结论中:①;②;③;④,其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
11.菱形的边长为5,对角线,则菱形的面积是 .
12.要使矩形ABCD成为正方形,可添加的条件是 (写一个即可).
13.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,则∠E=
14.如图,一张长,宽的矩形纸片,将它沿某直线折叠使得A、C重合,则折痕的长为 .
15.如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF= .
16.已知,矩形,点在边上,点在边上,连接、交于点.若,,,.则 .
17.如图,在平面直角坐标系中,四边形是边长为1的正方形,顶点分别在轴的正半轴上.点Q在对角线上,且,连接并延长交边于点P,则点P的坐标为 .
18.如图,有一张矩形纸片,已知,,现将纸片进行如下操作:现将纸片沿折痕进行折叠,使点落在边上的点处,点在上(如图),则 ;然后将绕点旋转到,当过点时旋转停止,则的长度为 .
三、解答题
19.如图,矩形的对角线,相交于点,过点作的平行线交的延长线于点.
(1)求证:.
(2)若,,求的长.
20.如图,平行四边形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F,且AE=DF.
(1)求证:四边形ABCD是矩形;
(2)若∠BAE∶∠EAD=2∶3,求∠EAO的度数.
21.如图,在平行四边形ABCD中,平分,交于点E,平分,交于点F,与交于点P,连结,.
(1)求证:四边形是菱形.
(2)若,,,求的值.
22.如图,在6×6的方格纸中,请按要求作图.
(1)图1中,A,B是方格纸中的格点,以AB为一边作一个矩形ABCD,要求C,D两点也在格点上;
(2)图2中,E,F是方格纸中的格点,以EF为一边作一个菱形EFGH,要求G,H两点也在格点上.
23.已知:如图,在正方形ABCD中,BD为对角线,E、F分别是AD,CD上的点,且AE=CF,连接BE、BF、EF.
(1)求证:EM=FM;
(2)若DE:AE=2:1,设S△ABE=S,求S△BEF(用含S的代数式表示).
24.在正方形ABCD中,AC是对角线,点E在AD边上(不与点A重合),点F在CD边上,连接BE,BF,EF,已知∠DEF=45°.
(1)求证:BE=BF.
(2)设AE=k AD(0<k<1),△ABE的面积为S1,△DEF的面积为S2.
①当k=时,求证:S1=2S2;
②当S2=2S1时,求k的值.
25.如图,在矩形中,,.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是.连接、、.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形是矩形,请说明理由;
(2)当t为何值时,四边形是菱形,请说明理由;
(3)直接写出(2)中菱形的周长和面积,周长是______cm,面积是______.
26.如图,在平行四边形ABCD中,,E,F分别为,的中点,作于点G,的延长线交的延长线于点H.
(1)求证:四边形是菱形.
(2)当时,
①求的长.
②如图2,交于点P,记的面积为,的面积为,则的值为________.
27.如图,在平面直角坐标系中,点A(0,8),点B是x轴的正半轴上的一个动点,连接AB,取AB的中点M,将线段MB绕着点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0)
(1)当t=6时,点M的坐标是______;
(2)求点C的坐标(用含t的代数式表示);
(3)是否存在点B,使四边形AOBD为矩形?若存在,请求出点B的坐标;若不存在,请说明理由;
(4)在点B的运动过程中,平面内是否存在一点N,使得以A、B、N、D为顶点的四边形是菱形?若存在,请直接写出点N的纵坐标(不必要写横坐标);若不存在,请说明理由.
28.正方形中,边长为,点在对角线上,连接,过点作,交直线于点.
(1)如图,当点在边上时,求证:;
(2)当点在的延长线上时,设,面积为,求关于的解析式,并写出定义域;
(3)若,求BM的长.
答案
一、单选题
1.B
【分析】本题考查了正方形和矩形的性质,解决本题的关键是熟记正方形和矩形的性质.对于四边形的性质我们从:①边;②角;③对角线三个方面去理解,因此,只需要根据正方形、矩形的这三个方面性质的不同,即可解答.
【解析】解:根据正方形和矩形的性质对比分析:
①边:有对边与邻边:正方形与矩形对边性质相同,没有区别;邻边性质不同,正方形邻边相等,矩形邻边不相等;
②角:正方形与矩形内角性质相同,对角相等、邻角互补、四个角都是直角;
③对角线:正方形与矩形对角线都相等且互相平分,但正方形对角线相互垂直,而矩形对角线不具有这个特征;
故选:B.
2.B
【分析】根据菱形的性质得到,,再进一步求解即可.
【解析】解:四边形是菱形,
,,
,
,
,
故选B.
3.B
【分析】根据矩形对角线相等且互相平分的性质和题中的条件易得△AOB为等边三角形,即可得到矩形对角线的长,进而求解即可.
【解析】
如图:AB=6,∠AOB=60°,
∵四边形是矩形,AC,BD是对角线,
∴OA=OB=OC=OD=BD=AC,
在△AOB中,OA=OB,∠AOB=60°,
∴OA=OB=AB=6,BD=2OB=12,
∴BC=.
故选:B.
4.C
【分析】根据菱形,矩形,正方形的性质和判定定理,逐个进行判断即可.
【解析】解:A、有一组邻边相等的平行四边形是菱形,故A不正确,不符合题意;
B、对角线互相垂直的平行四边形是菱形,故B不正确,不符合题意;
C、矩形的对角线相等,故C正确,符合题意;
D、对角线相等且互相垂直平分的四边形是正方形,故D不正确,不符合题意;
故选:C.
5.D
【分析】直接利用正方形的性质求解即可.
【解析】解:∵四边形是正方形,
∴,
∴,
故选:D.
6.D
【分析】首先利用菱形的性质结合勾股定理得出BC的长,再利用三角形面积求出答案
【解析】解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC==5(cm),
∵S△ABC=AE×BC=BO×AC
故5AE=24,
解得:AE=(cm).
故选D.
7.B
【分析】由EF垂直平分AC可得AE=CE,设CE=x,则ED=AD﹣AE=4﹣x,在Rt△CDE中,利用勾股定理求出x的长,继而根据三角形的面积公式进行求解即可.
【解析】∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=4,∠D=90°,
∵EO是AC的垂直平分线,
∴AE=CE,
设CE=x,则ED=AD﹣AE=4﹣x,
在Rt△CDE中,CE2=CD2+ED2,
即x2=22+(4﹣x)2,
解得:x=,
即CE的长为,
DE=4﹣=,
所以△DCE的面积=××2=,
故选B.
8.D
【分析】设点,根据正方形的性质可得,再代入求得,再根据,,列方程求解即可.
【解析】解:∵点B、C分别在两条直线和上,
设点,
∵四边形是正方形,
∴,
∴把代入得,,
∴,
∴,,
∴,
∴,
故选:D.
9.D
【分析】证明△ABE≌△DBF(AAS),可得AE=DF;结合图形可知:AE+CF=AB,AB是一定值,从而完成求解.
【解析】连接BD
∵四边形ABCD是菱形,
∴AB=AD=CD,
∵∠A=60°
∴△ABD是等边三角形
∴AB=BD,∠ABD=60°
∵DC∥AB
∴∠CDB=∠ABD=60°
∴∠A=∠CDB
∵∠EBF=60°
∴∠ABE+∠EBD=∠EBD+∠DBF
∴∠ABE=∠DBF
∵
∴△ABE≌△DBF(AAS)
∴AE=DF
∴AE+CF=DF+CF=CD=AB
故选:D.
10.C
【分析】先判断出∠DAE=∠ABH,再判断△ADE≌△CDE得出∠DAE=∠DCE=22.5°,∠ABH=∠DCF,再判断出△ABH≌△DCF从而得到①正确,根据三角形的外角求出∠AEF=45°,得出②正确;结合①②可得DF=DE,根据AH=DF即可得③正确;连接HE,判断出S△EFH≠S△EFD得出④错误.
【解析】解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在△ABH和△DCF中,
,
∴△ABH≌△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故①②正确;
∵∠FDE=45°,∠DFE=∠FAE+∠AEF=22.5°+45°=67.5°,
∴∠DEF=180°﹣45°﹣67.5°=67.5°,
∴DF=DE,
∵AH=DF,
∴AH=DE,故③正确;
如图,连接HE,
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故④错误,
∴正确的是①②③.
故选:C
二、填空题
11.24
【分析】根据菱形的对角线互相垂直,再利用勾股定理求出另一条对角线的长度,根据菱形的面积计算方法求解即可.
【解析】如图所示,
∵菱形的边长为5,
∴,,
又∵,
∴,
∴,
∴,
∴菱形的面积.
故答案为:24.
12.AB=BC;BC=CD;CD=AD;AD=AB;AC⊥BD(挑选一个即可)
【分析】根据正方形的判定定理进行添加即可.
【解析】从边上添加:有AB=BC,BC=CD,CD=DA,DA=AB(有一组领边相等的矩形为正方形)
从对角线上添加:有AC⊥BD(对角线互相垂直的矩形为正方形).
故答案为:AB=BC;BC=CD;CD=AD;AD=AB;AC⊥BD(挑选一个即可)
13.22.5 °
【分析】由于正方形的对角线平分一组对角,那么∠ACB=45°,即∠ACE=135°,在等腰△CAE中,已知了顶角的度数,即可由三角形内角和定理求得∠E的度数.
【解析】解:正方形对角线平分直角,故∠ACD=45°,
已知DC⊥CE,则∠ACE=∠135°,
又∵CE=AC,
∴∠E==22.5°.
故答案为:22.5°.
14.
【分析】由题意可知,连接,利用翻折的性质可知,,,进而可得,则,设,则,在中由勾股定理可得,列出方程即可求得,在中由勾股定理可得,进而可求得折痕的长度.
【解析】解:由题意可知,,,,
∴,
连接,
由翻折可知,,,,则,
∵,
∴,
∴,
∴,
设,则,
在中由勾股定理可得:,
即:,解得:,即:,
∴在中由勾股定理可得:,
∴.
故答案为:.
15.
【分析】连接OP.由勾股定理得出AC=10,可求得OA=OB=5,由矩形的性质得出S矩形ABCD=AB BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,由S△AOB=S△AOP+S△BOP=OA PE+OB PF=OA(PE+PF)=×5×(PE+PF)=12求得答案.
【解析】解:连接OP,如图:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC,OB=OD,AC=BD,
∴OA=OB,AC==10,
∴S矩形ABCD=AB BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,
∴S△AOB=S△AOP+S△BOP=OA PE+OB PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF=;
故答案为:.
16.6
【分析】过点作,垂足为,交于点H,证明,得出是等腰直角三角形,进而得出四边形是平行四边形,即可求解.
【解析】解:如图所示,过点作,垂足为,交于点H,
∵四边形是矩形,
∴,
∴,
∵,,,
∴,
∴
∴,,
∴是等腰直角三角形,
∴,
∵,
∴,
又∵,
∴四边形是平行四边形,
∴,
∴,
故答案为:6.
17.
【分析】首先根据正方形的性质得到对角线,结合题意推出,并由正方形的性质推出∠BPQ=∠BQP,得到,从而得到,即可得出结论.
【解析】解:∵四边形OABC是边长为1的正方形,
∴根据勾股定理,得对角线,
∵OQ=OC,
∴,∠OCQ=∠OQC,
∵OC//AB,
∴∠OCQ=∠BPQ,
∵∠OQC=∠BQP(对顶角相等),
∴∠BPQ=∠BQP,
∴,
∴,
又 ∵OA=1,
∴点P的坐标为,
故答案为:.
18. 2
【分析】连接,证四边形是正方形,得,进而得,,由勾股定理得,证明()得,,从而点垂直平分,点垂直平分,,最后利用面积公式构造方程即可得解.
【解析】解:∵四边形是矩形,
∴,,,
∵将纸片沿折痕进行折叠,使点落在边上的点处,点在上,
∴,,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,
∴,,
∴,
连接,
∵将绕点旋转到,
∴,,
∵,
∴()
∴,,
∴点垂直平分,点垂直平分,
∴,
∴,即,
∴,
故答案为:,.
三、解答题
19.(1)证明:四边形是矩形,
,,
.
,
四边形是平行四边形,
,
.
(2)解:四边形是矩形,
,,
.
∴
,
,
.
20.(1)解:∵,
∴
又∵,
∴△AEO≌△DFO
∴
∵四边形是平行四边形
∴
∴
∴四边形是矩形
(2)解:∵ ,是矩形
∴,
∴在中,
∴在中,
∴在中,
21.(1)∵在平行四边形ABCD中,平分,
∴∠BCE=∠DCE,∠BCE=∠DEC,
∴∠DCE=∠DEC,
∴DE=DC,
∵平分,
∴∠ADF=∠CDF,∠ADF=∠DFC,
∴∠CDF =∠DFC,
∴CF=DC=DE,
∵ED∥FC,
∴四边形是菱形;
(2)作PH⊥BC于点H,
∵∠BAD=120°,
∴∠PCH=60°,
∵四边形是菱形,AB=2,
∴CE=2,
∴CP=1,
∴CH=,PH=,
∵BC=3,
∴BH=,
∴.
22.解:(1)如图1,四边形ABCD即为所求作的矩形;
(2)如图2,四边形EFGH即为所求作的菱形;
.
23.(1)∵四边形ABCD是正方形,
∴,
又∵AE=CF,
∴,
∴是等腰三角形,
又∵,
∴EM=FM;
(2)∵DE:AE=2:1,
∴设,,,
∴,
∴,
同理可求得:,
∴,
∴.
24.(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠BCD=∠D=90°,AB=BC=CD=AD,
在Rt△DEF中,∠DEF=45°,
∴∠DFE=90°-∠DEF=45°=∠DEF,
∴DE=DF,
∴AD- DE=CD -DF,
∴AE=CF,
∴△ABE≌△CBF(SAS),
∴BE=BF;
(2)解:设AD=x,则AB=AD=x,
∵AE=k AD,
∴AE=k x,
∴DE=DF=AD- AE=x -kx=(1-k)x,
∴S1=AE AB=k x x=kx2,
S2=DE DF= [(1-k)x]2=(1-k)2x2,
①当k=时,S1=kx2=x2,
S2=(1-k)2x2=(1-)2x2=x2,
∴S1=2S2;
②当S2=2S1时,2×kx2=(1-k)2x2,
∴k=2+(由于0<k<1,所以,舍去)或k=2-,
即k=2-.
25.(1)解:由题意得,,则,
四边形是矩形,
,,
当时,四边形为矩形,
,
解得,,
故当时,四边形为矩形;
(2)解:由(1)可知,四边形为平行四边形,
当时,四边形为菱形,
即时,四边形为菱形,
解得,,
故当时,四边形为菱形;
(3)解:当时,,
菱形的周长为:,
菱形的面积为:,
故答案为:15;.
26.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E、F分别为BC、AD中点,
∴AF=AD,BE=BC,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AD=2AB,AD=2AF,
∴AB=AF,
∴四边形ABEF是菱形;
(2)①连接AE交BF于点O,
∵四边形ABEF是菱形,
∴AE⊥BF,OB=OF=BE=4,OA=OE=AE,
∴∠AOB=90°,
在Rt△AOB中,OA==3,
∴AE=2OA=6,
∴S菱形ABEF=AE·BF=×6×8=24,
∵E、F分别是BC、AD中点,
∴BE=EC,AF=FD,
∵AD∥BC,
∴四边形ABEF,四边形EFDC都是平行四边形,且底和高相等,
∴S四边形ABEF=S四边形EFDC=24,
∴S四边形ABCD=S四边形ABEF+S四边形EFDC=48,
∵CG⊥AB,
∴S四边形ABEF=AB·CG=5CG=48,∠BGC=90°,
∴CG=,
∵AD=BC=2AB=10,
∴BG=,
∴AG=AB -BG=5-=,
∵四边形ABCD是平行四边形,
∴AB=CD=5,AB∥CD,
∴∠A=∠FDH,∠GCH=∠BGC=90°,
∵F是AD中点,
∴AF=DF,
在△AFG和△DFH中,
,
∴△AFG≌△DFH(ASA),
∴AG=DH=,
∴CH=CD+DH=5+=,
在Rt△GCH中,GH==12;
②过F作FK⊥AB交BA延长线于K,
∴S四边形ABEF=AB·FK=5FK=24,
∴FK=,
∴S△BGF=BG·FK==,
S△BGC=BG·CG==,
∵S2=S△BGC -S△BGP=-S△BGP,
S1=S△BGF -S△BGP=-S△BGP,
∴S2-S1=-=.
27.(1)如图1中,
,,,
,
故答案为:(3,4);
(2)如图1中,作于,轴于.
∵,
,,
,
,,
,
,
,
,,
,
.
(3)存在.
如图2中,作于,轴于.
理由:由题意当时,
,
四边形是平行四边形,
,
四边形是矩形,
,
四边形是矩形,
又∵由(2)得,
即:,解得:.
.
(4)①如图3中,当时,以为对角线可得菱形,此时点在轴上.作BE⊥AC交于点E,
设,,
∵点M是AB的中点,,
∴,
∵,,,
∴,
∴,
∴,
在中,则有,
①②联立,解得:,
,
点的纵坐标为3.
②如图4中,当时,以为对角线可得菱形.此时点的纵坐标为8.
③,
不存在以为对角线的菱形.
综上所述,满足条件的点的纵坐标为3或8.
28.(1)过点作于点,于点,
,
四边形是正方形,
,,
,
,
,
,
,
,
,
;
(2)过点作于点,交于点.
,
在正方形中,,,
四边形为矩形,
,,,
,
,
,
,
在中,,,
,
,
,
又,,
,
,
,
,
,
,
;
(3)当点在边上时,连接,交于,过作于,
在正方形中,,,
,
在中,,则,
∵S BNM= BM NE,,且,
,
∵∠AOB=900,
,
,
,
又,
,
,
,
当点在的延长线上时,同理可得.
