16.1.1同位角、内错角、同旁内角 同步练习(含解析)2024-2025学年七年级下册沪教版(五四学制)(2024)
文档属性
| 名称 | 16.1.1同位角、内错角、同旁内角 同步练习(含解析)2024-2025学年七年级下册沪教版(五四学制)(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 648.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 11:51:59 | ||
图片预览


文档简介
16.1.1同位角、内错角、同旁内角
一、单选题
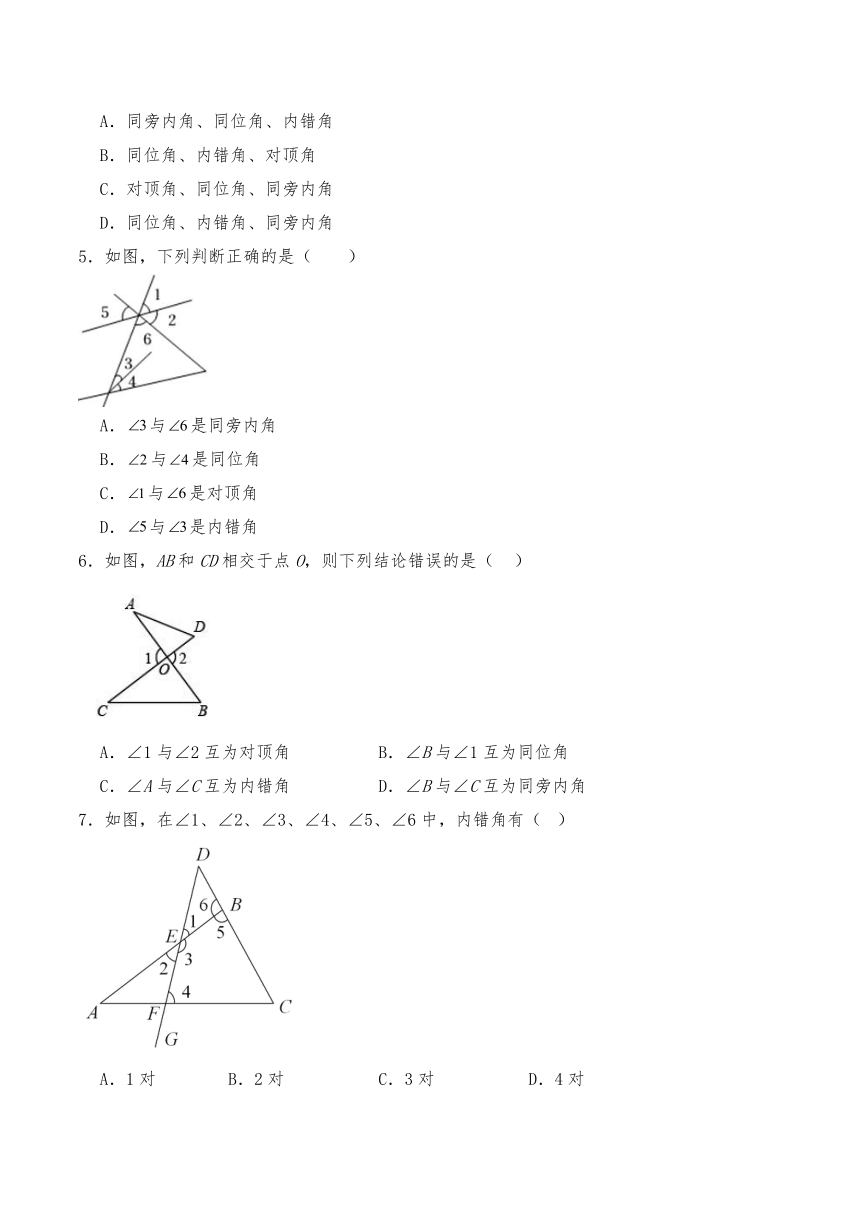
1.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( ).
A.∠1 B.∠2
C.∠4 D.∠5
2.下列四个图形中,和是内错角的是( )
A. B.
C. D.
3.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
4.数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
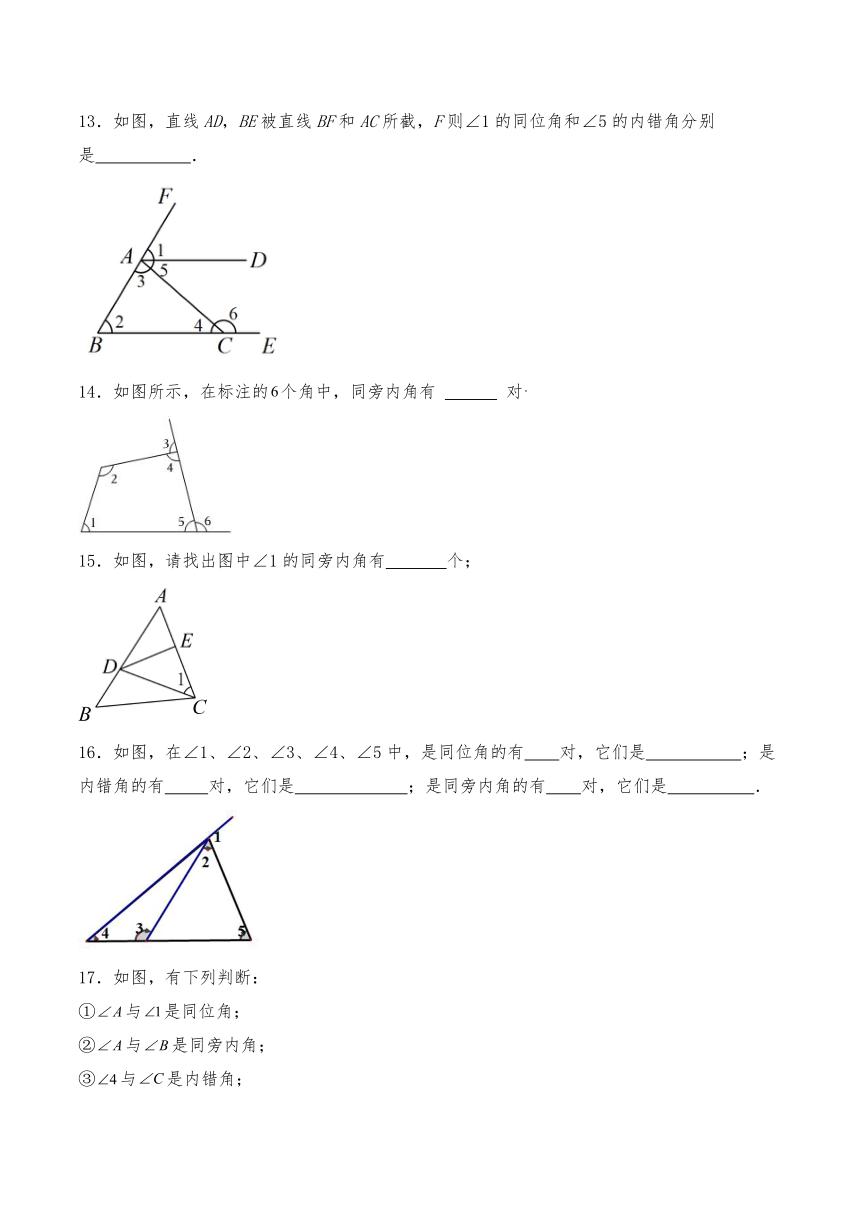
5.如图,下列判断正确的是( )
A.与是同旁内角
B.与是同位角
C.与是对顶角
D.与是内错角
6.如图,AB和CD相交于点O,则下列结论错误的是( )
A.∠1与∠2互为对顶角 B.∠B与∠1互为同位角
C.∠A与∠C互为内错角 D.∠B与∠C互为同旁内角
7.如图,在∠1、∠2、∠3、∠4、∠5、∠6中,内错角有( )
A.1对 B.2对 C.3对 D.4对
8.如图,在∠1、∠2、∠3、∠4中,内错角是( )
A.与 B.与
C.与 D.与
9.中国滑雪天才少女谷爱凌在2022年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金,这是她获得的首个冬奥会奖牌,也是中国运动员第一次参加冬奥会大跳台的比赛.项目图标如下图;则在下列判断中①∠1与∠2是对顶角;②∠3与∠4是同旁内角;③∠5与∠6是同旁内角;④∠1与∠4是内错角,其中正确的有( )个.
A.1 B.2 C.3 D.4
10.若平面上5条直线两两相交,且无三线共点,无四线共点,则一共有多少对同旁内角( )
A.59 B.60 C.61 D.62
二、填空题
11.如图所示的四个图形中,和是同位角的是 .(填序号)
12.如图,∠2与∠3是直线 、 被第三条直线 所截形成的 .
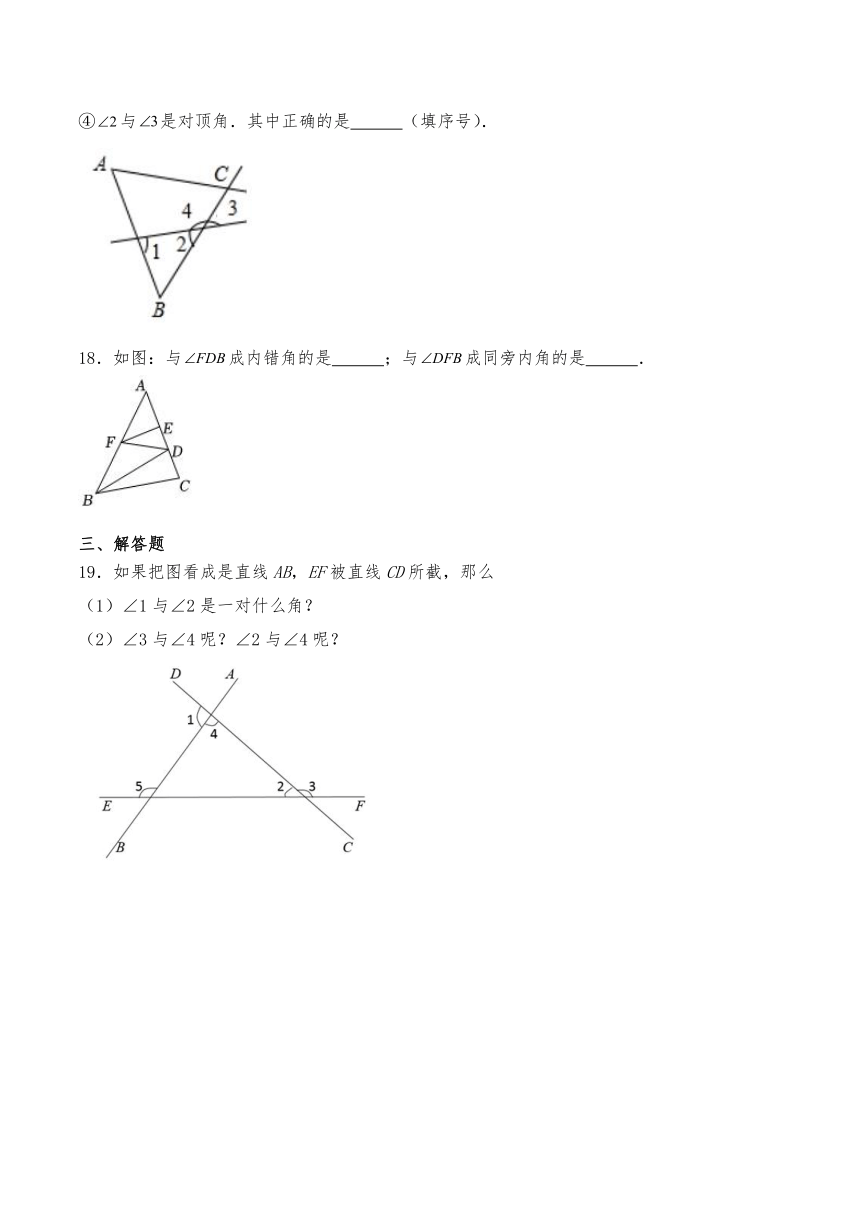
13.如图,直线AD,BE被直线BF和AC所截,F则∠1的同位角和∠5的内错角分别是 .
14.如图所示,在标注的个角中,同旁内角有 对
15.如图,请找出图中∠1的同旁内角有 个;
16.如图,在∠1、∠2、∠3、∠4、∠5中,是同位角的有 对,它们是 ;是内错角的有 对,它们是 ;是同旁内角的有 对,它们是 .
17.如图,有下列判断:
①与是同位角;
②与是同旁内角;
③与是内错角;
④与是对顶角.其中正确的是 (填序号).
18.如图:与成内错角的是 ;与成同旁内角的是 .
三、解答题
19.如果把图看成是直线AB,EF被直线CD所截,那么
(1)∠1与∠2是一对什么角?
(2)∠3与∠4呢?∠2与∠4呢?
20.如图,与,与,与,与,与分别是哪两条直线被哪一条直线所截得到的?它们中的每一对角分别叫做什么角?
21.如图,说出与,与,与与分别是哪两条直线被哪一条直线所截得的,各是什么角?
22.如图,试判断∠1与∠2,∠1与∠7,∠1与∠BAD,∠2与∠9,∠2与∠6,∠5与∠8各对角的位置关系.
23.根据图形填空:
(1)若直线被直线所截,则和_____是同位角;
(2)若直线被直线所截,则和_____是内错角;
(3)和是直线被直线______所截构成的内错角;
(4)和是直线,______被直线所截构成的_____角.
24.(1)指出下列各图中的与是同位角、内错角还是同旁内角.
① ② ③ ④
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么?
25.已知:如图是一个跳棋棋盘,其游戏规则是一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上例如:从起始位置跳到终点位置有两种不同路径,路径1:;路径2:.
试一试:(1)写出从起始位置跳到终点位置的一种路径;
(2)从起始位置依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置?
答案
一、单选题
1.B
【分析】根据同旁内角就是:两个角都在截线的同旁,又分别处在被截的两条直线之间位置的角解答即可.
【解析】根据同旁内角的定义可得∠3的内错角是∠2.
故答案选:B
2.B
【分析】根据内错角的概念:处于两条被截直线之间,截线的两侧,再逐一判断即可.
【解析】解:A、∠1与∠2不是内错角,选项不符合题意;
B、∠1与∠2是内错角,选项符合题意;
C、∠1与∠2不是内错角,选项不符合题意;
D、∠1和∠2不是内错角,选项不符合题意;
故选:B.
3.B
【分析】同位角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角;内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角.根据此定义即可得出答案.
【解析】解:∵直线AD,BE被直线BF和AC所截,
∴∠1与∠2是同位角,∠5与∠6是内错角,
故选:B.
4.D
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.据此作答即可.
【解析】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
5.A
【分析】根据同位角、同旁内角、内错角和对顶角的概念解答即可.
【解析】解:A、与是同旁内角,故本选项符合题意;
B、与不是同位角,故本选项不合题意;
C、与不是对顶角,故本选项不合题意;
D、与不是内错角,故本选项不合题意;
故选:A.
6.C
【分析】根据对顶角、同位角、内错角、同旁内角定义判断求解即可.
【解析】解:∠1与∠2互为对顶角,
故A正确,不符合题意;
∠B与∠1互为同位角,
故B正确,不符合题意;
∠A 与∠C不是内错角,
故C错误,符合题意;
∠B与∠C互为同旁内角,
故D正确,不符合题意;
故选:C.
7.C
【分析】根据定义判断内错角的对数即可.
【解析】解: ∵直线DC、直线DG被直线AB所截,
∴∠1和∠5是内错角,∠3和∠6是内错角;
∵直线AB、直线AC被直线DG所截,
∴∠2和∠4是内错角;
∴有3对内错角.
故选:C.
8.D
【分析】根据内错角的定义找出即可.
【解析】解:根据内错角的定义,∠2与∠3是内错角,
故选:D.
9.C
【分析】利用对顶角、同旁内角、内错角的定义逐个判断即可.
【解析】解:∠1与∠2有公共顶点且两条边都互为反向延长线,因此是对顶角,故①正确;
两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角,因此∠3与∠4是同旁内角,故②正确;
∠5与∠6是邻补角,不是同旁内角,故③错误;
两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫作内错角,因此∠1与∠4是内错角,故④正确;
综上,正确的有①②④.
故选C.
10.B
【分析】每条直线都与另4条直线相交,且没有3条直线交于一点,共有30条线段.每条线段两侧各有一对同旁内角内角,可知同旁内角的总对数.
【解析】解:如图,
∵平面上5条直线两两相交,且无三线共点,无四线共点,
∴共有5×6=30条线段.
又∵每条线段两侧各有一对同旁内角内角,
∴共有同旁内角30×2=60对.
故选:B
二、填空题
11.①②④
【分析】根据同位角的定义,逐一判断选项,即可得到答案.
【解析】解:①∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;
②∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;
③∠1与∠2分别是四条直线中的两对直线的夹角,不符合同位角的定义,故它们不是同位角;
④∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角.
故答案为:①②④.
12. AB AC BD 同旁内角
【分析】根据同旁内角的定义即可判断.
【解析】由同旁内角的概念可知:
如图所示,∠2与∠3是直线AB,AC被直线BD所截而成的同旁内角;
故答案为:AB;AC;BD;同旁内角;
13.∠2和∠4
【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角进行分析即可.
根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角进行分析即可.
【解析】解:∠1的同位角是∠2,∠5的内错角是∠4,
故答案为:∠2和∠4.
14.4
【分析】根据同旁内角的定义判断即可,两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的同旁,则这样一对角叫做同旁内角.
【解析】解:和是同旁内角,
和是同旁内角,
和是同旁内角,
和是同旁内角,
故在标注的个角中,同旁内角有对.
故答案为:.
15.4
【分析】根据同旁内角的定义,两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角.
【解析】解:∠1的同旁内角有,共4个
故答案为:4
16. 2 ∠1和∠4、∠3和∠5 2 ∠1与∠5、∠2与∠3 3 ∠2和∠5、∠3和∠4、∠4和∠5
【分析】根据同位角、内错角和同旁内角的概念进行解答.
【解析】解:如图,由题意可得:
同位角有:2对,分别是:∠1和∠4、∠3和∠5;
内错角有:2对,分别是:∠1与∠5、∠2与∠3;
同旁内角有:3对,分别是:∠2和∠5、∠3和∠4、∠4和∠5.
17.①②④
【分析】根据同位角、同旁内角、内错角、对顶角的定义判断即可.
【解析】解:①由同位角的概念得出,与是同位角,正确;
②由同旁内角的概念得出,与是同旁内角,正确;
③由同旁内角的概念得出,与是同旁内角,错误;
④由对顶角的概念得出,与是对顶角,正确.
故正确的是①②④.
故答案为:①②④.
18. 、和 、、和
【分析】准确识别内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【解析】解:如图,与成内错角的是、和,与成同旁内角的是:、、和.
故答案分别是:、和,、、和.
三、解答题
19.解:直线AB,EF被直线CD所截,
(1)∠1与∠2是一对同位角;
(2)∠3与∠4是一对内错角,∠2与∠4是一对同旁内角.
20.解:与是直线和直线被直线所截得到的内错角;
与是直线和直线被直线所截得到的同位角;
与是直线和直线被直线所截得到的内错角;
与是直线和直线被直线所截得到的同旁内角;
与是直线和直线被直线所截得到的同旁内角.
21.解:与是直线和直线被直线所截得的同位角;
与是直线和直线被直线所截得的内错角;
与是直线和直线被直线所截得的同旁内角;
与是直线和直线被直线所截得的同旁内角
22.由图可知:∠1与∠2是同旁内角.
∠1与∠7是同位角.
∠1与∠BAD是同旁内角.
∠2与∠9没有特殊的位置关系.
∠2与∠6是内错角.
∠5与∠8是对顶角.
23.解:由图可得:
(1)若直线被直线所截,则和是同位角;
故答案为;
(2)若直线被直线所截,则和是内错角;
故答案为;
(3)和是直线被直线所截构成的内错角;
故答案为;
(4)和是直线,被直线所截构成的同位角;
故答案为,同位.
24.(1)①与是内错角;②与是同旁内角;③与是同位角;④与是同位角.
故答案为:内错角,同旁内角,同位角,同位角;
(2)辨认同位角、内错角、同旁内角的方法:在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中主线是截线,抓住了截线,再利用图形结构特征,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形进行判断.
25.(1)可以是这样的路径:.(答案不唯一)
(2)从起始位置依次按同位角内错角同旁内角的顺序跳,能跳到终点位置.其路径为
(答案不唯一).
一、单选题
1.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( ).
A.∠1 B.∠2
C.∠4 D.∠5
2.下列四个图形中,和是内错角的是( )
A. B.
C. D.
3.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
4.数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
5.如图,下列判断正确的是( )
A.与是同旁内角
B.与是同位角
C.与是对顶角
D.与是内错角
6.如图,AB和CD相交于点O,则下列结论错误的是( )
A.∠1与∠2互为对顶角 B.∠B与∠1互为同位角
C.∠A与∠C互为内错角 D.∠B与∠C互为同旁内角
7.如图,在∠1、∠2、∠3、∠4、∠5、∠6中,内错角有( )
A.1对 B.2对 C.3对 D.4对
8.如图,在∠1、∠2、∠3、∠4中,内错角是( )
A.与 B.与
C.与 D.与
9.中国滑雪天才少女谷爱凌在2022年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金,这是她获得的首个冬奥会奖牌,也是中国运动员第一次参加冬奥会大跳台的比赛.项目图标如下图;则在下列判断中①∠1与∠2是对顶角;②∠3与∠4是同旁内角;③∠5与∠6是同旁内角;④∠1与∠4是内错角,其中正确的有( )个.
A.1 B.2 C.3 D.4
10.若平面上5条直线两两相交,且无三线共点,无四线共点,则一共有多少对同旁内角( )
A.59 B.60 C.61 D.62
二、填空题
11.如图所示的四个图形中,和是同位角的是 .(填序号)
12.如图,∠2与∠3是直线 、 被第三条直线 所截形成的 .
13.如图,直线AD,BE被直线BF和AC所截,F则∠1的同位角和∠5的内错角分别是 .
14.如图所示,在标注的个角中,同旁内角有 对
15.如图,请找出图中∠1的同旁内角有 个;
16.如图,在∠1、∠2、∠3、∠4、∠5中,是同位角的有 对,它们是 ;是内错角的有 对,它们是 ;是同旁内角的有 对,它们是 .
17.如图,有下列判断:
①与是同位角;
②与是同旁内角;
③与是内错角;
④与是对顶角.其中正确的是 (填序号).
18.如图:与成内错角的是 ;与成同旁内角的是 .
三、解答题
19.如果把图看成是直线AB,EF被直线CD所截,那么
(1)∠1与∠2是一对什么角?
(2)∠3与∠4呢?∠2与∠4呢?
20.如图,与,与,与,与,与分别是哪两条直线被哪一条直线所截得到的?它们中的每一对角分别叫做什么角?
21.如图,说出与,与,与与分别是哪两条直线被哪一条直线所截得的,各是什么角?
22.如图,试判断∠1与∠2,∠1与∠7,∠1与∠BAD,∠2与∠9,∠2与∠6,∠5与∠8各对角的位置关系.
23.根据图形填空:
(1)若直线被直线所截,则和_____是同位角;
(2)若直线被直线所截,则和_____是内错角;
(3)和是直线被直线______所截构成的内错角;
(4)和是直线,______被直线所截构成的_____角.
24.(1)指出下列各图中的与是同位角、内错角还是同旁内角.
① ② ③ ④
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么?
25.已知:如图是一个跳棋棋盘,其游戏规则是一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上例如:从起始位置跳到终点位置有两种不同路径,路径1:;路径2:.
试一试:(1)写出从起始位置跳到终点位置的一种路径;
(2)从起始位置依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置?
答案
一、单选题
1.B
【分析】根据同旁内角就是:两个角都在截线的同旁,又分别处在被截的两条直线之间位置的角解答即可.
【解析】根据同旁内角的定义可得∠3的内错角是∠2.
故答案选:B
2.B
【分析】根据内错角的概念:处于两条被截直线之间,截线的两侧,再逐一判断即可.
【解析】解:A、∠1与∠2不是内错角,选项不符合题意;
B、∠1与∠2是内错角,选项符合题意;
C、∠1与∠2不是内错角,选项不符合题意;
D、∠1和∠2不是内错角,选项不符合题意;
故选:B.
3.B
【分析】同位角:两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,我们把这样的两个角称为同位角;内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角.根据此定义即可得出答案.
【解析】解:∵直线AD,BE被直线BF和AC所截,
∴∠1与∠2是同位角,∠5与∠6是内错角,
故选:B.
4.D
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.据此作答即可.
【解析】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
5.A
【分析】根据同位角、同旁内角、内错角和对顶角的概念解答即可.
【解析】解:A、与是同旁内角,故本选项符合题意;
B、与不是同位角,故本选项不合题意;
C、与不是对顶角,故本选项不合题意;
D、与不是内错角,故本选项不合题意;
故选:A.
6.C
【分析】根据对顶角、同位角、内错角、同旁内角定义判断求解即可.
【解析】解:∠1与∠2互为对顶角,
故A正确,不符合题意;
∠B与∠1互为同位角,
故B正确,不符合题意;
∠A 与∠C不是内错角,
故C错误,符合题意;
∠B与∠C互为同旁内角,
故D正确,不符合题意;
故选:C.
7.C
【分析】根据定义判断内错角的对数即可.
【解析】解: ∵直线DC、直线DG被直线AB所截,
∴∠1和∠5是内错角,∠3和∠6是内错角;
∵直线AB、直线AC被直线DG所截,
∴∠2和∠4是内错角;
∴有3对内错角.
故选:C.
8.D
【分析】根据内错角的定义找出即可.
【解析】解:根据内错角的定义,∠2与∠3是内错角,
故选:D.
9.C
【分析】利用对顶角、同旁内角、内错角的定义逐个判断即可.
【解析】解:∠1与∠2有公共顶点且两条边都互为反向延长线,因此是对顶角,故①正确;
两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角,因此∠3与∠4是同旁内角,故②正确;
∠5与∠6是邻补角,不是同旁内角,故③错误;
两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫作内错角,因此∠1与∠4是内错角,故④正确;
综上,正确的有①②④.
故选C.
10.B
【分析】每条直线都与另4条直线相交,且没有3条直线交于一点,共有30条线段.每条线段两侧各有一对同旁内角内角,可知同旁内角的总对数.
【解析】解:如图,
∵平面上5条直线两两相交,且无三线共点,无四线共点,
∴共有5×6=30条线段.
又∵每条线段两侧各有一对同旁内角内角,
∴共有同旁内角30×2=60对.
故选:B
二、填空题
11.①②④
【分析】根据同位角的定义,逐一判断选项,即可得到答案.
【解析】解:①∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;
②∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;
③∠1与∠2分别是四条直线中的两对直线的夹角,不符合同位角的定义,故它们不是同位角;
④∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角.
故答案为:①②④.
12. AB AC BD 同旁内角
【分析】根据同旁内角的定义即可判断.
【解析】由同旁内角的概念可知:
如图所示,∠2与∠3是直线AB,AC被直线BD所截而成的同旁内角;
故答案为:AB;AC;BD;同旁内角;
13.∠2和∠4
【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角进行分析即可.
根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角进行分析即可.
【解析】解:∠1的同位角是∠2,∠5的内错角是∠4,
故答案为:∠2和∠4.
14.4
【分析】根据同旁内角的定义判断即可,两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的同旁,则这样一对角叫做同旁内角.
【解析】解:和是同旁内角,
和是同旁内角,
和是同旁内角,
和是同旁内角,
故在标注的个角中,同旁内角有对.
故答案为:.
15.4
【分析】根据同旁内角的定义,两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角.
【解析】解:∠1的同旁内角有,共4个
故答案为:4
16. 2 ∠1和∠4、∠3和∠5 2 ∠1与∠5、∠2与∠3 3 ∠2和∠5、∠3和∠4、∠4和∠5
【分析】根据同位角、内错角和同旁内角的概念进行解答.
【解析】解:如图,由题意可得:
同位角有:2对,分别是:∠1和∠4、∠3和∠5;
内错角有:2对,分别是:∠1与∠5、∠2与∠3;
同旁内角有:3对,分别是:∠2和∠5、∠3和∠4、∠4和∠5.
17.①②④
【分析】根据同位角、同旁内角、内错角、对顶角的定义判断即可.
【解析】解:①由同位角的概念得出,与是同位角,正确;
②由同旁内角的概念得出,与是同旁内角,正确;
③由同旁内角的概念得出,与是同旁内角,错误;
④由对顶角的概念得出,与是对顶角,正确.
故正确的是①②④.
故答案为:①②④.
18. 、和 、、和
【分析】准确识别内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【解析】解:如图,与成内错角的是、和,与成同旁内角的是:、、和.
故答案分别是:、和,、、和.
三、解答题
19.解:直线AB,EF被直线CD所截,
(1)∠1与∠2是一对同位角;
(2)∠3与∠4是一对内错角,∠2与∠4是一对同旁内角.
20.解:与是直线和直线被直线所截得到的内错角;
与是直线和直线被直线所截得到的同位角;
与是直线和直线被直线所截得到的内错角;
与是直线和直线被直线所截得到的同旁内角;
与是直线和直线被直线所截得到的同旁内角.
21.解:与是直线和直线被直线所截得的同位角;
与是直线和直线被直线所截得的内错角;
与是直线和直线被直线所截得的同旁内角;
与是直线和直线被直线所截得的同旁内角
22.由图可知:∠1与∠2是同旁内角.
∠1与∠7是同位角.
∠1与∠BAD是同旁内角.
∠2与∠9没有特殊的位置关系.
∠2与∠6是内错角.
∠5与∠8是对顶角.
23.解:由图可得:
(1)若直线被直线所截,则和是同位角;
故答案为;
(2)若直线被直线所截,则和是内错角;
故答案为;
(3)和是直线被直线所截构成的内错角;
故答案为;
(4)和是直线,被直线所截构成的同位角;
故答案为,同位.
24.(1)①与是内错角;②与是同旁内角;③与是同位角;④与是同位角.
故答案为:内错角,同旁内角,同位角,同位角;
(2)辨认同位角、内错角、同旁内角的方法:在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中主线是截线,抓住了截线,再利用图形结构特征,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形进行判断.
25.(1)可以是这样的路径:.(答案不唯一)
(2)从起始位置依次按同位角内错角同旁内角的顺序跳,能跳到终点位置.其路径为
(答案不唯一).
同课章节目录
