复数的几何意义
图片预览



文档简介
课件10张PPT。复数的几何意义问题情境 这样,复数z=a+bi(a,b∈R)与有序实数对(a,b))之间可以建立一一对应,
有序实数对(a,b)和平面直角坐标系中的点Z(a,b)之间也可以建立一一对应.
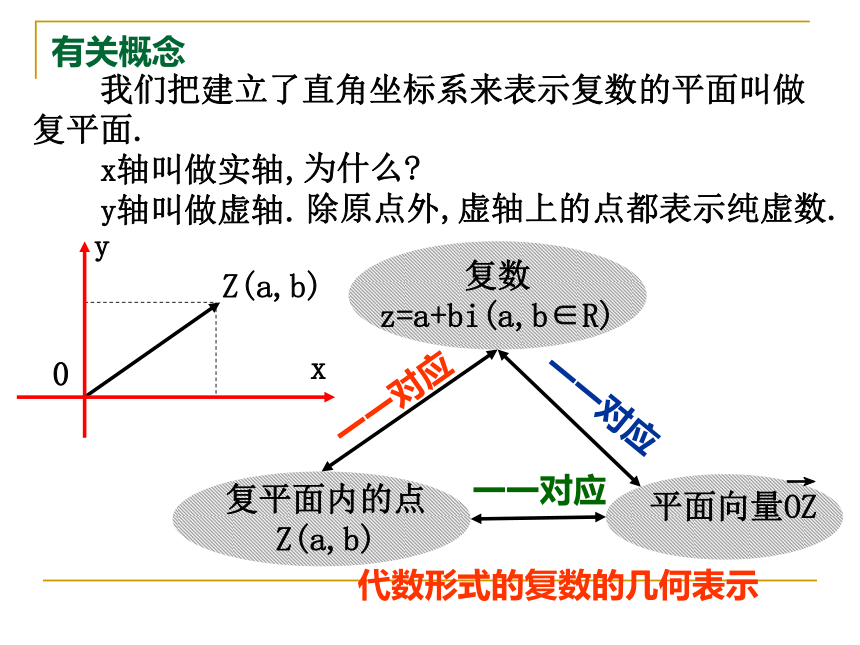
因此,复数z=a+bi(a,b∈R)也就可以用点来表示. 已知复数z=2+7i,则复数z=2+7i确定唯一一个有序实数对(2,7),直角坐标系中有序实数对(2,7)确定唯一一个点Z(2,7).反之亦然.有关概念 我们把建立了直角坐标系来表示复数的平面叫做复平面.
x轴叫做实轴,
y轴叫做虚轴.为什么?除原点外,虚轴上的点都表示纯虚数.复数
z=a+bi(a,b∈R)复平面内的点
Z(a,b) →
平面向量OZ
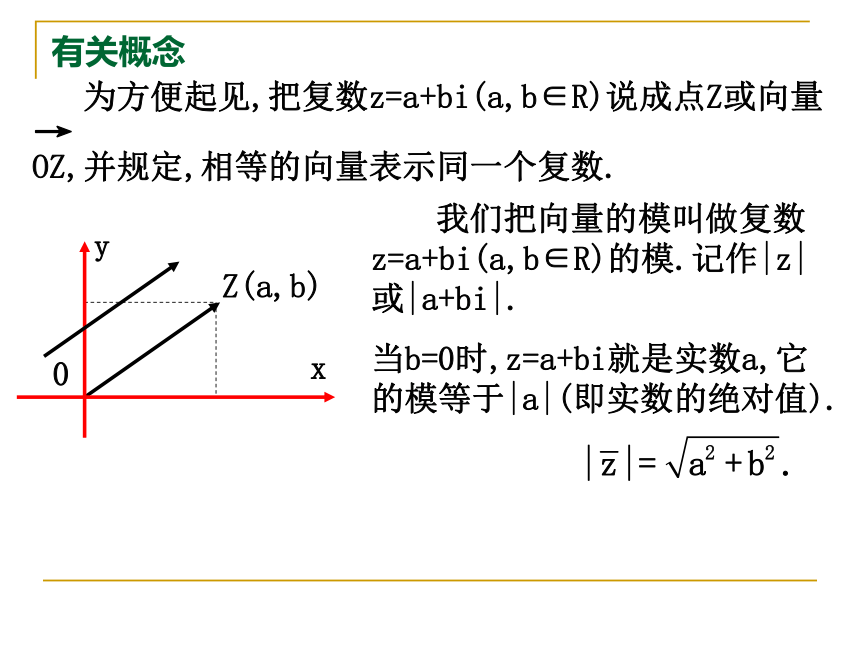
一一对应一一对应一一对应代数形式的复数的几何表示有关概念 为方便起见,把复数z=a+bi(a,b∈R)说成点Z或向量→
OZ,并规定,相等的向量表示同一个复数. 我们把向量的模叫做复数z=a+bi(a,b∈R)的模.记作|z|或|a+bi|.
当b=0时,z=a+bi就是实数a,它的模等于|a|(即实数的绝对值).复数模的性质1.z =|z|2= . 2.|z1·z2|=|z1||z2|; ; ; .例题讲解例1.在复平面内,分别用点和向量表示下列复数:
4, 2+i,-i, -1+3i, 3-2i.
并求出这些复数的模.
例2.已知复数z1=3+4i,z2=-1+5i.试比较z1,z2模的大小.
例3.设z∈C,满足下列条件的点Z的集合是什么图形?
(1)|z|=2; (2)|z-z1|=2; (3)2<|z|<3.例题讲解例4.复数z=log2(x2-3x-3)+ilog2(x-3),设z在复平面上
对应的点为Z.
(1)求证:复数z不能是纯虚数;
(2)若点Z在第三象限,求x的取值范围;
(3)若点Z在直线x-2y+1=0上,求x的值.例5.设复数z满足|z|=5,且(3+4i)z在复平面上对应的点
在第二、第四象限角平分线上,
求z和m的值.问题探究 请作出复数z1=1-i,z2=2+3i及z1+z2对应的以原点为起点的向量,由此你能受到什么启发?将得出什么一般结论?
复数加法与减法的几何意义 → →
设向量OZ1,OZ2分别与复数z1=x1+y1i,z2=x2+y2i
→ → → →
对应,且OZ1,OZ2不共线,则以向量OZ1,OZ2为邻边的平行
→
四边形的对角线OZ对应的复数是z1+z2.
→
向量Z1Z2对应的复数是z2-z1.
→
于是|z2-z1|=|Z1Z2|
=这样的结果似曾相识.请作说明. → →
以复数z1,z2对应的向量OZ1,OZ2为邻边作平行四边
形,则|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2).复数加法与减法的几何意义
有序实数对(a,b)和平面直角坐标系中的点Z(a,b)之间也可以建立一一对应.
因此,复数z=a+bi(a,b∈R)也就可以用点来表示. 已知复数z=2+7i,则复数z=2+7i确定唯一一个有序实数对(2,7),直角坐标系中有序实数对(2,7)确定唯一一个点Z(2,7).反之亦然.有关概念 我们把建立了直角坐标系来表示复数的平面叫做复平面.
x轴叫做实轴,
y轴叫做虚轴.为什么?除原点外,虚轴上的点都表示纯虚数.复数
z=a+bi(a,b∈R)复平面内的点
Z(a,b) →
平面向量OZ
一一对应一一对应一一对应代数形式的复数的几何表示有关概念 为方便起见,把复数z=a+bi(a,b∈R)说成点Z或向量→
OZ,并规定,相等的向量表示同一个复数. 我们把向量的模叫做复数z=a+bi(a,b∈R)的模.记作|z|或|a+bi|.
当b=0时,z=a+bi就是实数a,它的模等于|a|(即实数的绝对值).复数模的性质1.z =|z|2= . 2.|z1·z2|=|z1||z2|; ; ; .例题讲解例1.在复平面内,分别用点和向量表示下列复数:
4, 2+i,-i, -1+3i, 3-2i.
并求出这些复数的模.
例2.已知复数z1=3+4i,z2=-1+5i.试比较z1,z2模的大小.
例3.设z∈C,满足下列条件的点Z的集合是什么图形?
(1)|z|=2; (2)|z-z1|=2; (3)2<|z|<3.例题讲解例4.复数z=log2(x2-3x-3)+ilog2(x-3),设z在复平面上
对应的点为Z.
(1)求证:复数z不能是纯虚数;
(2)若点Z在第三象限,求x的取值范围;
(3)若点Z在直线x-2y+1=0上,求x的值.例5.设复数z满足|z|=5,且(3+4i)z在复平面上对应的点
在第二、第四象限角平分线上,
求z和m的值.问题探究 请作出复数z1=1-i,z2=2+3i及z1+z2对应的以原点为起点的向量,由此你能受到什么启发?将得出什么一般结论?
复数加法与减法的几何意义 → →
设向量OZ1,OZ2分别与复数z1=x1+y1i,z2=x2+y2i
→ → → →
对应,且OZ1,OZ2不共线,则以向量OZ1,OZ2为邻边的平行
→
四边形的对角线OZ对应的复数是z1+z2.
→
向量Z1Z2对应的复数是z2-z1.
→
于是|z2-z1|=|Z1Z2|
=这样的结果似曾相识.请作说明. → →
以复数z1,z2对应的向量OZ1,OZ2为邻边作平行四边
形,则|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2).复数加法与减法的几何意义
