数学质量监测题(三) 图形的平移与旋转(含答案)2024-2025学年八年级下册数学北师大版(2024)
文档属性
| 名称 | 数学质量监测题(三) 图形的平移与旋转(含答案)2024-2025学年八年级下册数学北师大版(2024) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 12:04:07 | ||
图片预览


文档简介
2024-2025八下数学质量监测题(三)图形的平移与旋转
一、选择题(每小题3分,共30分)
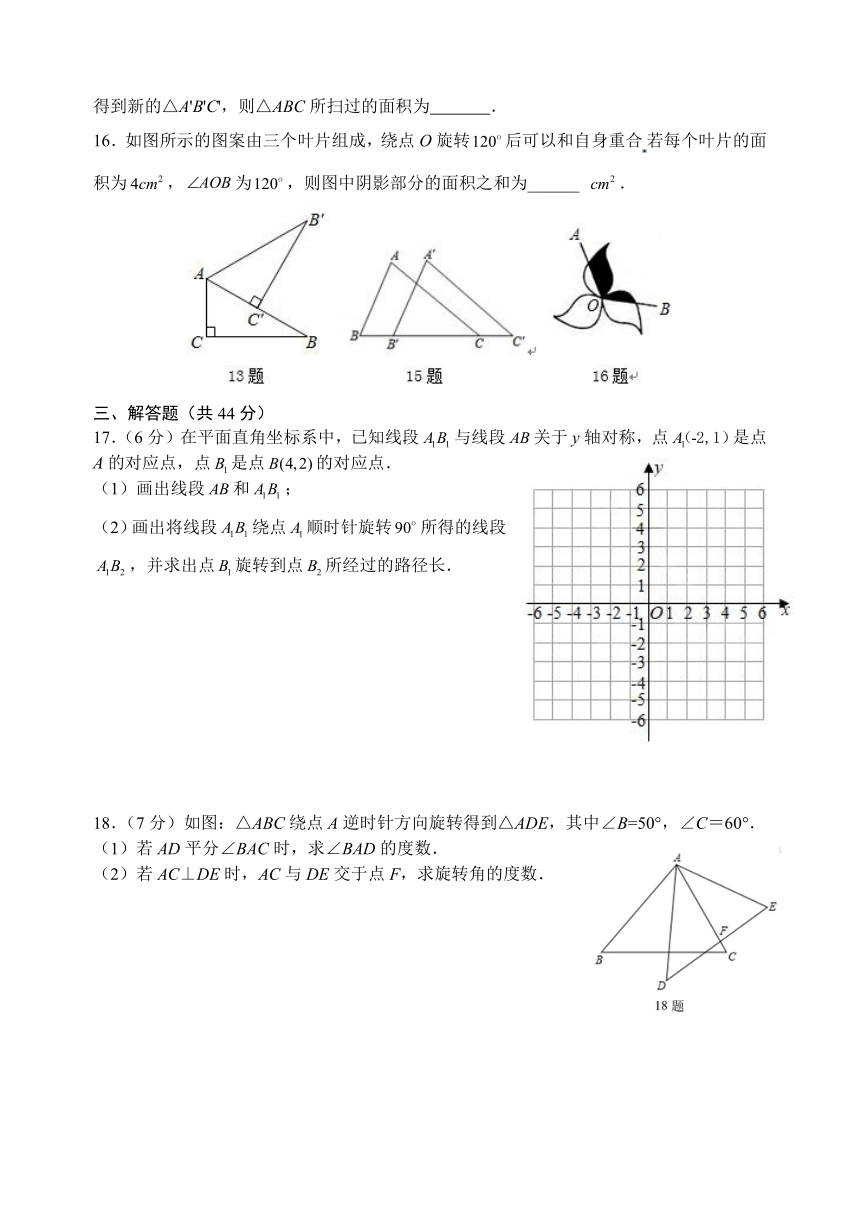
1.下列图形中,属于中心对称图形的是( )
A. B. C. D.
2.如图,在平面内将五角星绕其中心旋转后所得到的图案是( )
A. B. C. D.
3.如图,在中,,将绕点O逆时针方向旋转,得到,连接,则线段的长为( )
A. 1 B. C. D.
4.在平面直角坐标系中,点A(a,1)与点B(﹣2,b)关于原点成中心对称,则a+b的值为( )
A.﹣3 B.﹣1 C.1 D.3
3题 5题 6题
5.如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
6.如图,两个灯笼的位置的坐标分别是,将点向右平移2个单位,再向上平移1个单位得到点,则关于点的位置描述正确是( )
A.关于轴对称 B.关于轴对称
C.关于原点对称 D.关于直线对称
7.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
7题 8题 10题
8.如图,中,,将逆时针旋转得到,交于F.当时,点D恰好落在上,此时等于( )
A. B. C. D.
9.在平面直角坐标系中,将点先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点A在y轴上,点B的坐标为,将绕着点B顺时针旋转,得到,则点C的坐标是( )
A. B. C. D.
二、填空题(11-14小题4分,15-16小题5分,共26分)
11.在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是 .
12.把直线沿x轴向右平移2个单位,所得直线的函数解析式为 .
13.如图,在中,,,,将绕点A逆时针旋转角得到,并使点落在边上,则点所经过的路径长为______ .(结果保留)
14.在平面直角坐标系中,将点A(4,2)绕原点逆时针方向旋转90°后,其对应点A′的坐标为 .
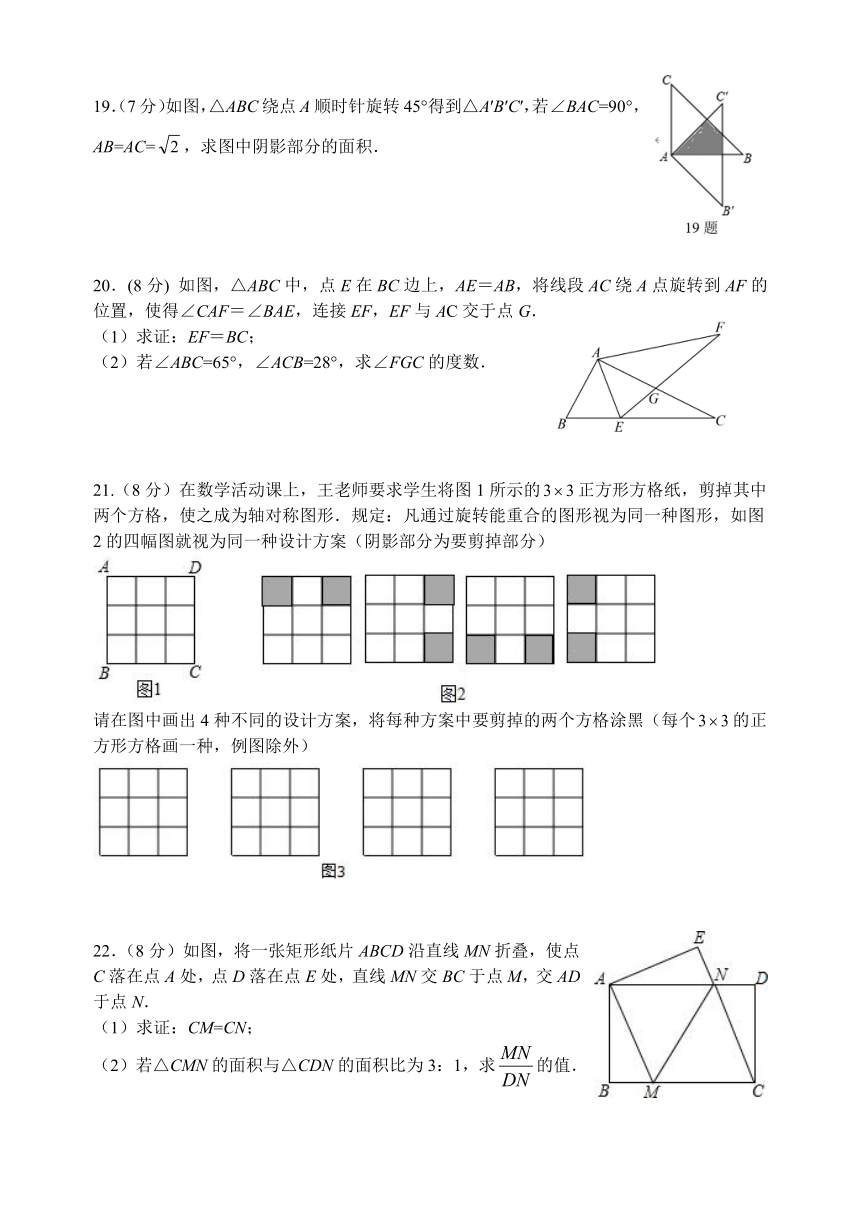
15.如图,△ABC的面积为10,BC=4,现将△ABC沿着射线BC平移a个单位(a>0),得到新的△A'B'C',则△ABC所扫过的面积为 .
16.如图所示的图案由三个叶片组成,绕点O旋转后可以和自身重合若每个叶片的面积为,为,则图中阴影部分的面积之和为______ .
三、解答题(共44分)
17.(6分)在平面直角坐标系中,已知线段与线段关于y轴对称,点是点A的对应点,点是点的对应点.
(1)画出线段和;
(2)画出将线段绕点顺时针旋转所得的线段,并求出点旋转到点所经过的路径长.
18.(7分)如图:△ABC绕点A逆时针方向旋转得到△ADE,其中∠B=50°,∠C=60°.
(1)若AD平分∠BAC时,求∠BAD的度数.
(2)若AC⊥DE时,AC与DE交于点F,求旋转角的度数.
19.(7分)如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=,求图中阴影部分的面积.
20.(8分) 如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
21.(8分)在数学活动课上,王老师要求学生将图1所示的正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个的正方形方格画一种,例图除外)
22.(8分)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,求的值.
参考答案
一、选择题
1.B. 2.C. 3.B. 4.C. 5.C.6.B.7.C. 8.B. 9.D.10.B.
二、填空题
11.6 12. 13. 14.(﹣2,4) 15.解:△ABC所扫过面积即梯形ABC′A′的面积,作AH⊥BC于H,
∴S△ABC=10,BC AH=10,AH=5,
∴S梯形ABFD=×(AA′+BC′)×AH
=(a+4+a)×5
=10+5a;
故答案为:10+5a.
16.4.
三、解答题
17.【答案】解:如图,线段和为所作;
如图,线段为所作,
,
所以点旋转到点所经过的路径长
18.解:,,
,
平分,
;
绕点逆时针方向旋转得到,
,旋转角为,
,
,
旋转角为.
19.解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=,
∴BC=2,∠C=∠B=∠CAC′=∠C′=45°,
∴AD⊥BC,B′C′⊥AB,
∴AD=BC=1,AF=FC′=AC′=1,
∴图中阴影部分的面积等于:S△AFC′﹣S△DEC′=×1×1﹣×(﹣1)2=﹣1.
20.解:证明:,
.
将线段绕点旋转到的位置,
.
在与中,
,
≌,
.
,,
,
.
≌,
,
.
21. 【解题过程】解:如图所示,
22.(1)证明:由折叠的性质可得:∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN;
(2)解:过点N作NH⊥BC于点H,
则四边形NHCD是矩形,
∴HC=DN,NH=DC,
∵△CMN的面积与△CDN的面积比为3:1,
∴===3,
∴MC=3ND=3HC,
∴MH=2HC,
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN,
在Rt△CDN中,DC==2x,
∴HN=2x,
在Rt△MNH中,MN==2x,
∴==2.
PAGE
一、选择题(每小题3分,共30分)
1.下列图形中,属于中心对称图形的是( )
A. B. C. D.
2.如图,在平面内将五角星绕其中心旋转后所得到的图案是( )
A. B. C. D.
3.如图,在中,,将绕点O逆时针方向旋转,得到,连接,则线段的长为( )
A. 1 B. C. D.
4.在平面直角坐标系中,点A(a,1)与点B(﹣2,b)关于原点成中心对称,则a+b的值为( )
A.﹣3 B.﹣1 C.1 D.3
3题 5题 6题
5.如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
6.如图,两个灯笼的位置的坐标分别是,将点向右平移2个单位,再向上平移1个单位得到点,则关于点的位置描述正确是( )
A.关于轴对称 B.关于轴对称
C.关于原点对称 D.关于直线对称
7.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
7题 8题 10题
8.如图,中,,将逆时针旋转得到,交于F.当时,点D恰好落在上,此时等于( )
A. B. C. D.
9.在平面直角坐标系中,将点先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点A在y轴上,点B的坐标为,将绕着点B顺时针旋转,得到,则点C的坐标是( )
A. B. C. D.
二、填空题(11-14小题4分,15-16小题5分,共26分)
11.在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是 .
12.把直线沿x轴向右平移2个单位,所得直线的函数解析式为 .
13.如图,在中,,,,将绕点A逆时针旋转角得到,并使点落在边上,则点所经过的路径长为______ .(结果保留)
14.在平面直角坐标系中,将点A(4,2)绕原点逆时针方向旋转90°后,其对应点A′的坐标为 .
15.如图,△ABC的面积为10,BC=4,现将△ABC沿着射线BC平移a个单位(a>0),得到新的△A'B'C',则△ABC所扫过的面积为 .
16.如图所示的图案由三个叶片组成,绕点O旋转后可以和自身重合若每个叶片的面积为,为,则图中阴影部分的面积之和为______ .
三、解答题(共44分)
17.(6分)在平面直角坐标系中,已知线段与线段关于y轴对称,点是点A的对应点,点是点的对应点.
(1)画出线段和;
(2)画出将线段绕点顺时针旋转所得的线段,并求出点旋转到点所经过的路径长.
18.(7分)如图:△ABC绕点A逆时针方向旋转得到△ADE,其中∠B=50°,∠C=60°.
(1)若AD平分∠BAC时,求∠BAD的度数.
(2)若AC⊥DE时,AC与DE交于点F,求旋转角的度数.
19.(7分)如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=,求图中阴影部分的面积.
20.(8分) 如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
21.(8分)在数学活动课上,王老师要求学生将图1所示的正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个的正方形方格画一种,例图除外)
22.(8分)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,求的值.
参考答案
一、选择题
1.B. 2.C. 3.B. 4.C. 5.C.6.B.7.C. 8.B. 9.D.10.B.
二、填空题
11.6 12. 13. 14.(﹣2,4) 15.解:△ABC所扫过面积即梯形ABC′A′的面积,作AH⊥BC于H,
∴S△ABC=10,BC AH=10,AH=5,
∴S梯形ABFD=×(AA′+BC′)×AH
=(a+4+a)×5
=10+5a;
故答案为:10+5a.
16.4.
三、解答题
17.【答案】解:如图,线段和为所作;
如图,线段为所作,
,
所以点旋转到点所经过的路径长
18.解:,,
,
平分,
;
绕点逆时针方向旋转得到,
,旋转角为,
,
,
旋转角为.
19.解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=,
∴BC=2,∠C=∠B=∠CAC′=∠C′=45°,
∴AD⊥BC,B′C′⊥AB,
∴AD=BC=1,AF=FC′=AC′=1,
∴图中阴影部分的面积等于:S△AFC′﹣S△DEC′=×1×1﹣×(﹣1)2=﹣1.
20.解:证明:,
.
将线段绕点旋转到的位置,
.
在与中,
,
≌,
.
,,
,
.
≌,
,
.
21. 【解题过程】解:如图所示,
22.(1)证明:由折叠的性质可得:∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN;
(2)解:过点N作NH⊥BC于点H,
则四边形NHCD是矩形,
∴HC=DN,NH=DC,
∵△CMN的面积与△CDN的面积比为3:1,
∴===3,
∴MC=3ND=3HC,
∴MH=2HC,
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN,
在Rt△CDN中,DC==2x,
∴HN=2x,
在Rt△MNH中,MN==2x,
∴==2.
PAGE
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
