2025年九年级中考数学基础知识专项训练题4 平面直角坐标系、函数(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题4 平面直角坐标系、函数(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 823.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览





文档简介
2025中考数学基础知识专项训练题4 平面直角坐标系、函数
选择题:(每小题3分,共30分)
1.在平面直角坐标系中,点A(1,2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
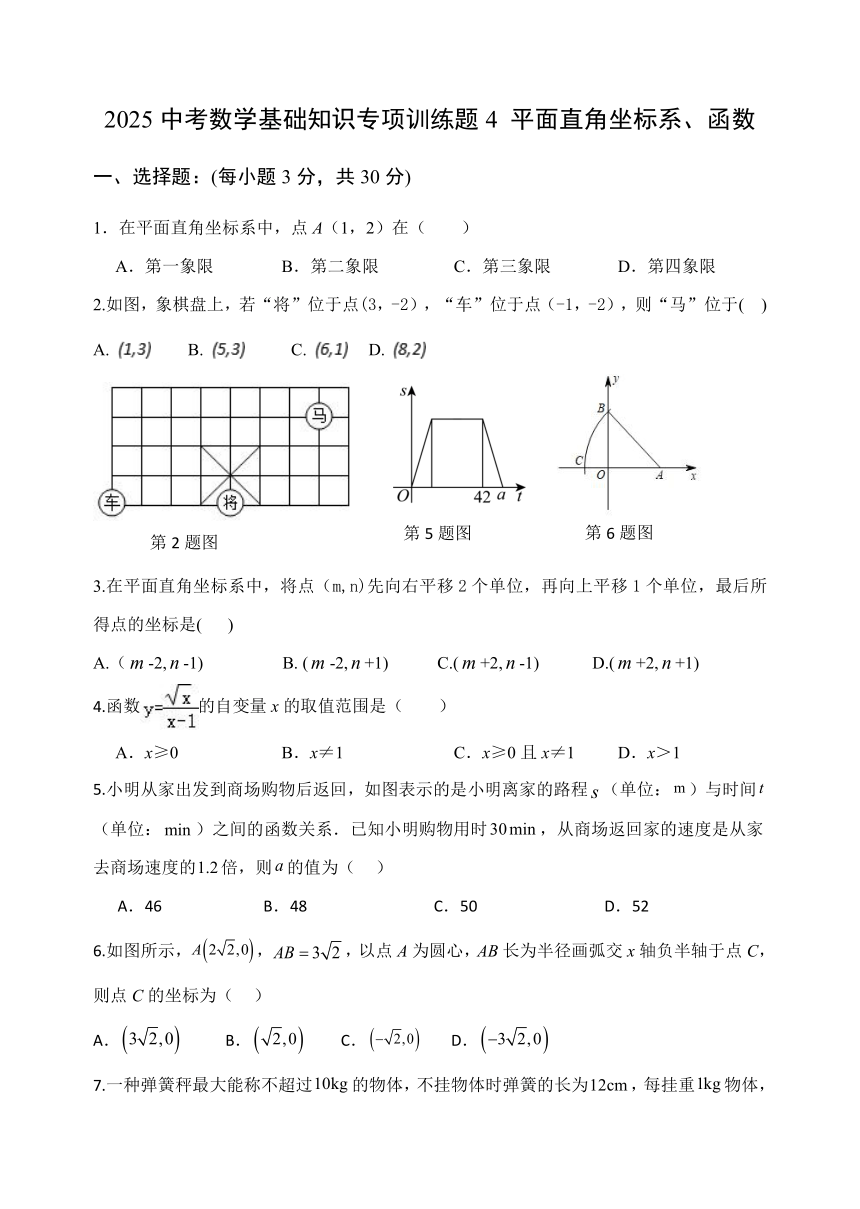
2.如图,象棋盘上,若“将”位于点(3,-2),“车”位于点(-1,-2),则“马”位于( )
A. B. C. D.
3.在平面直角坐标系中,将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A.(-2,-1) B. (-2,+1) C.(+2,-1) D.(+2,+1)
4.函数的自变量x的取值范围是( )
A.x≥0 B.x≠1 C.x≥0且x≠1 D.x>1
5.小明从家出发到商场购物后返回,如图表示的是小明离家的路程(单位:)与时间(单位:)之间的函数关系.已知小明购物用时,从商场返回家的速度是从家去商场速度的倍,则的值为( )
A.46 B.48 C.50 D.52
6.如图所示,,,以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( )
A. B. C. D.
7.一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为,每挂重物体,弹簧伸长.在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )
A. B. C. D.
8.如图①,在矩形ABCD中(BC>AB),连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,y与x的函数关系图象如图②所示,则边BC的长为( )
A.4 B.3 C.5 D.8
9.数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算时,用到了一种方法,将首尾两个数相加,进而得到1+2+3+4+…+100=.人们借助于这样的方法,1+2+3+4+…+n=.(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点,其中,且是整数.记,如,即,即,即,以此类推.则下列结论正确的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,O为原点,OA=OB=3,点C为平面内一动点,BC=,连接AC,点M是线段AC上的一点,且满足CM:MA=1:2.当线段OM取最大值时,点M的坐标是( )
A.(,) B.(,) C.(,) D.(,)
二、填空题(11-14每小题4分,15-16每小题5分,共26分)
11.在平面直角坐标系中,点P(-4,5)到y轴的距离是 .
12.若点M(+3,-1)在第四象限,则的取值范围是______.
13.若点N(+5,)在y轴上,则点N的坐标是___________.
14.在直角坐标系中,已知两点A(0,2),B(4,1),点P是轴上一点,则PA+PB的最小值是 .
15.如图所示的网格由边长为1个单位长度的小正方形组成,点、、在直角坐标系中的坐标分别为,,,则内心的坐标为 .
16.如图1,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图2所示,当x=(s)时,则
y= cm2.
三、解答题(共64分,17-20每题10分,21-22题每题12分)
17.已知点A(-3,5)和B(2, b-2),试根据下列条件求出a,b的值.
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB//x轴.
18.如图、在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在第三象限内画一个△A2B2C2,使它与△ABC的相似比为,并写出点B2的坐标.
19.合肥市某超市经销某种特色水果的成本为每千克20元,一段时间内,销售单价P(元/千克)与时间t(天)的函数图象如图,且其日销售量y(千克)与时间t(天)的关系是:y=﹣2t+120(其中天数t为整数).
(1)当0≤t≤40天,求销售单价P(元/kg)与时间t(天)之间的函数关系式;
(2)问哪一天的销售利润最大?最大日销售利润为多少?
20.如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,顶点D在y轴的正半轴上,M为BC的中点,OA、OB的长分别是一元二次方程的两个根,,动点P从点D出发以每秒1个单位长度的速度沿折线向点B运动,到达B点停止.设运动时间为t秒,的面积为S.
(1)求点C的坐标;
(2)求S关于t的函数关系式,并写出自变量t的取值范围;
(3)在点P的运动过程中,是否存在点P,使是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
21.如图,在长方形中,为平面直角坐标系的原点,点的坐标为,点的坐标为,点在第一象限内,点从原点出发,以每秒个单位长度的速度沿着的路线移动一周,设点移动的时间为.
写出点的坐标;
在移动过程中,当点到轴的距离为时,求点移动的时间;
当三角形的面积为时,直接写出点的坐标.
22.如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(-5,0),且,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为秒.
(1)求A、C两点的坐标;
(2)连接PA,用含的代数式表示△POA的面积;
(3)当P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出的值并直接写出Q点坐标;若不存在,请说明理由.
参考答案
一、选择题:
1.A 2.C 3.D 4.C 5.D 6.C 7.B 8.A 9.B 10. D
二、填空题:
11.4 12. -3<<1 13. (0,-7) 14. 15
16
三、解答题:
17.解:(1)A、B两点关于轴对称,则
,
∴,=7
(2)A、B两点关于轴对称,则
,
∴,=-3
(3)AB//轴,则
,
∴,=7
18.解:(1)如图,为所作.
(2)如图,为所作,点B2的坐标为(-4,-6).
19. 解:解:(1)当0≤t≤40时,设P与t之间的函数关系式为P=kt+b.将坐标(0,30)和(40,40)代入,
得,解得.
∴当0≤t≤40时,P与t之间的函数关系式为P=t+30(0≤t≤40).
(2)设每千克这种特色水果的日销售利润为W元.
∴当0≤t≤40时,W=(P﹣20)y=(t+10)(﹣2t+120)=﹣(t﹣10)2+1250,
当t=10时,W有最大值为1250.
当t>40时,W=(P﹣20)y=20(﹣2t+120)=﹣40t+2400<800.
∴第10天的销售利润最大,最大日销售利润为1250元.
20.解:(1),解得,,
∵,
∴,,
∵,
∴,
∴,
∵四边形ABCD是平行四边形,
∴,,
∴点C坐标为;
(2)解:当时,,
当时,过点A作交CB的延长线于点F,如图,
,
∵四边形ABCD是平行四边形,
∴,
∵,
∴,
∴,
∴,
∴;
(3)
解:存在点P,使是等腰三角形,理由如下:
根据题意得:当点P在CD上运动时,可能是等腰三角形,
∵四边形ABCD是平行四边形,
∴∠C=∠BAD,BC=AD=5,
∴,
∵点M为BC的中点,
∴,
当CP=PM时,过点M作MF⊥PC于点F,
∴,
设PC=PM=a,则PD=7-a,,
∵PF2+FM2=PM2,
∴,解得:,
∴,
∴此时点P;
当时,
∴,
∴此时点P;
当PM=CM时,过点M作MG⊥PC于点G,则,
∴,
∴PD=7-PC=4,
∴此时点P;
综上所述,存在点P或或,使是等腰三角形
解:(1)∵A点的坐标为(4,0),C点的坐标为(0,6),
∴OA=4,OC=6
四边形ABCD是矩形,
∴AB=OC=6,BC=OA=4,,
点B(4,6);
(2)当点P到轴的距离为5时,OP=5或OC+CB+BP=11,
点P移动的时间为s或s.
(3)如图,
①当点P在OC上时,==8,
∴=4, ∴点P(0,4);
②当点P在BC上,==8,
∴,∴,
∴点P(,6);
③当点P在AB上==8,,
∴,∴
∴点P(4,2);
④当点P在AO上,==8,
∴=,点P(,0),
综上,点P的坐标为(0,4)或(,6)或(4,2)或(,0).
22. (1)∵,
∴n-3=0,3m-12=0,
n=3,m=4,
∴A的坐标是(0,4),C的坐标是(3,0);
(2)∵B(-5,0),
∴OB=5,
①当0≤t<时,P在线段OB上,如图1,
∵OP=5-2t,OA=4,
∴△POA的面积S=×OP×AP=×(5-2t)×4=10-4t;
②当t=时,P和O重合,此时△APO不存在,即S=0;
③当t>时,P在射线OC上,如备用图2,
∵OP=2t-5,OA=4,
∴△POA的面积S=×OP×AP=×(2t-5)×4=4t-10;
(3)当P在线段BO上运动时,在y轴上存在点Q,使△POQ与△AOC全等,
∵P在线段BO上运动,
∴t≤5÷2=2.5,
①当BP=1,OQ=3时,△POQ和△AOC全等,
此时t=,Q的坐标是(0,3);
②当BP=2,OQ=4时,△POQ和△AOC全等,
此时t==1,Q的坐标是(0,4);
③④由对称性可知Q为(0,-3)、(0,-4)
综上所述,t=或1时,Q的坐标是(0,3)或(0,4)或(0,-3)或
(0,-4).
第6题图
第2题图
第5题图
第9题图
第10题图
第8题图
第16题图
第15题图
PAGE
选择题:(每小题3分,共30分)
1.在平面直角坐标系中,点A(1,2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,象棋盘上,若“将”位于点(3,-2),“车”位于点(-1,-2),则“马”位于( )
A. B. C. D.
3.在平面直角坐标系中,将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A.(-2,-1) B. (-2,+1) C.(+2,-1) D.(+2,+1)
4.函数的自变量x的取值范围是( )
A.x≥0 B.x≠1 C.x≥0且x≠1 D.x>1
5.小明从家出发到商场购物后返回,如图表示的是小明离家的路程(单位:)与时间(单位:)之间的函数关系.已知小明购物用时,从商场返回家的速度是从家去商场速度的倍,则的值为( )
A.46 B.48 C.50 D.52
6.如图所示,,,以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( )
A. B. C. D.
7.一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为,每挂重物体,弹簧伸长.在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )
A. B. C. D.
8.如图①,在矩形ABCD中(BC>AB),连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,y与x的函数关系图象如图②所示,则边BC的长为( )
A.4 B.3 C.5 D.8
9.数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算时,用到了一种方法,将首尾两个数相加,进而得到1+2+3+4+…+100=.人们借助于这样的方法,1+2+3+4+…+n=.(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点,其中,且是整数.记,如,即,即,即,以此类推.则下列结论正确的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,O为原点,OA=OB=3,点C为平面内一动点,BC=,连接AC,点M是线段AC上的一点,且满足CM:MA=1:2.当线段OM取最大值时,点M的坐标是( )
A.(,) B.(,) C.(,) D.(,)
二、填空题(11-14每小题4分,15-16每小题5分,共26分)
11.在平面直角坐标系中,点P(-4,5)到y轴的距离是 .
12.若点M(+3,-1)在第四象限,则的取值范围是______.
13.若点N(+5,)在y轴上,则点N的坐标是___________.
14.在直角坐标系中,已知两点A(0,2),B(4,1),点P是轴上一点,则PA+PB的最小值是 .
15.如图所示的网格由边长为1个单位长度的小正方形组成,点、、在直角坐标系中的坐标分别为,,,则内心的坐标为 .
16.如图1,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图2所示,当x=(s)时,则
y= cm2.
三、解答题(共64分,17-20每题10分,21-22题每题12分)
17.已知点A(-3,5)和B(2, b-2),试根据下列条件求出a,b的值.
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB//x轴.
18.如图、在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在第三象限内画一个△A2B2C2,使它与△ABC的相似比为,并写出点B2的坐标.
19.合肥市某超市经销某种特色水果的成本为每千克20元,一段时间内,销售单价P(元/千克)与时间t(天)的函数图象如图,且其日销售量y(千克)与时间t(天)的关系是:y=﹣2t+120(其中天数t为整数).
(1)当0≤t≤40天,求销售单价P(元/kg)与时间t(天)之间的函数关系式;
(2)问哪一天的销售利润最大?最大日销售利润为多少?
20.如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,顶点D在y轴的正半轴上,M为BC的中点,OA、OB的长分别是一元二次方程的两个根,,动点P从点D出发以每秒1个单位长度的速度沿折线向点B运动,到达B点停止.设运动时间为t秒,的面积为S.
(1)求点C的坐标;
(2)求S关于t的函数关系式,并写出自变量t的取值范围;
(3)在点P的运动过程中,是否存在点P,使是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
21.如图,在长方形中,为平面直角坐标系的原点,点的坐标为,点的坐标为,点在第一象限内,点从原点出发,以每秒个单位长度的速度沿着的路线移动一周,设点移动的时间为.
写出点的坐标;
在移动过程中,当点到轴的距离为时,求点移动的时间;
当三角形的面积为时,直接写出点的坐标.
22.如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(-5,0),且,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为秒.
(1)求A、C两点的坐标;
(2)连接PA,用含的代数式表示△POA的面积;
(3)当P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出的值并直接写出Q点坐标;若不存在,请说明理由.
参考答案
一、选择题:
1.A 2.C 3.D 4.C 5.D 6.C 7.B 8.A 9.B 10. D
二、填空题:
11.4 12. -3<<1 13. (0,-7) 14. 15
16
三、解答题:
17.解:(1)A、B两点关于轴对称,则
,
∴,=7
(2)A、B两点关于轴对称,则
,
∴,=-3
(3)AB//轴,则
,
∴,=7
18.解:(1)如图,为所作.
(2)如图,为所作,点B2的坐标为(-4,-6).
19. 解:解:(1)当0≤t≤40时,设P与t之间的函数关系式为P=kt+b.将坐标(0,30)和(40,40)代入,
得,解得.
∴当0≤t≤40时,P与t之间的函数关系式为P=t+30(0≤t≤40).
(2)设每千克这种特色水果的日销售利润为W元.
∴当0≤t≤40时,W=(P﹣20)y=(t+10)(﹣2t+120)=﹣(t﹣10)2+1250,
当t=10时,W有最大值为1250.
当t>40时,W=(P﹣20)y=20(﹣2t+120)=﹣40t+2400<800.
∴第10天的销售利润最大,最大日销售利润为1250元.
20.解:(1),解得,,
∵,
∴,,
∵,
∴,
∴,
∵四边形ABCD是平行四边形,
∴,,
∴点C坐标为;
(2)解:当时,,
当时,过点A作交CB的延长线于点F,如图,
,
∵四边形ABCD是平行四边形,
∴,
∵,
∴,
∴,
∴,
∴;
(3)
解:存在点P,使是等腰三角形,理由如下:
根据题意得:当点P在CD上运动时,可能是等腰三角形,
∵四边形ABCD是平行四边形,
∴∠C=∠BAD,BC=AD=5,
∴,
∵点M为BC的中点,
∴,
当CP=PM时,过点M作MF⊥PC于点F,
∴,
设PC=PM=a,则PD=7-a,,
∵PF2+FM2=PM2,
∴,解得:,
∴,
∴此时点P;
当时,
∴,
∴此时点P;
当PM=CM时,过点M作MG⊥PC于点G,则,
∴,
∴PD=7-PC=4,
∴此时点P;
综上所述,存在点P或或,使是等腰三角形
解:(1)∵A点的坐标为(4,0),C点的坐标为(0,6),
∴OA=4,OC=6
四边形ABCD是矩形,
∴AB=OC=6,BC=OA=4,,
点B(4,6);
(2)当点P到轴的距离为5时,OP=5或OC+CB+BP=11,
点P移动的时间为s或s.
(3)如图,
①当点P在OC上时,==8,
∴=4, ∴点P(0,4);
②当点P在BC上,==8,
∴,∴,
∴点P(,6);
③当点P在AB上==8,,
∴,∴
∴点P(4,2);
④当点P在AO上,==8,
∴=,点P(,0),
综上,点P的坐标为(0,4)或(,6)或(4,2)或(,0).
22. (1)∵,
∴n-3=0,3m-12=0,
n=3,m=4,
∴A的坐标是(0,4),C的坐标是(3,0);
(2)∵B(-5,0),
∴OB=5,
①当0≤t<时,P在线段OB上,如图1,
∵OP=5-2t,OA=4,
∴△POA的面积S=×OP×AP=×(5-2t)×4=10-4t;
②当t=时,P和O重合,此时△APO不存在,即S=0;
③当t>时,P在射线OC上,如备用图2,
∵OP=2t-5,OA=4,
∴△POA的面积S=×OP×AP=×(2t-5)×4=4t-10;
(3)当P在线段BO上运动时,在y轴上存在点Q,使△POQ与△AOC全等,
∵P在线段BO上运动,
∴t≤5÷2=2.5,
①当BP=1,OQ=3时,△POQ和△AOC全等,
此时t=,Q的坐标是(0,3);
②当BP=2,OQ=4时,△POQ和△AOC全等,
此时t==1,Q的坐标是(0,4);
③④由对称性可知Q为(0,-3)、(0,-4)
综上所述,t=或1时,Q的坐标是(0,3)或(0,4)或(0,-3)或
(0,-4).
第6题图
第2题图
第5题图
第9题图
第10题图
第8题图
第16题图
第15题图
PAGE
同课章节目录
