2025年九年级中考数学基础知识专项训练题5 一次函数(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题5 一次函数(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 18:30:10 | ||
图片预览




文档简介
2025中考数学基础知识专项训练题5 一次函数
一、选择题(每小题3分,共30分)
1.下列各点在函数y=2x﹣1图象上的是( )
A.(﹣1,3) B.(0,1) C.(1,﹣1) D.(2,3)
2.已知一次函数的图象如图所示,则,的取值范围是( )
A., B., C., D.,
3.如图,直线y=ax+b(a≠0)过点A(0,3),B(4,0),则不等式ax+b>0的解集是( )
A.x>4 B.x<4 C.x>3 D.x<3
4.下列一次函数中,y随x的增大而减小的函数是( )
A.y=2x+1 B.y=x﹣4 C.y=2x D.y=﹣x+1
5.在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大 B.b<n
C.当x<2时,y1>y2 D.关于x,y的方程组的解为
6.在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=﹣2x+3 B.y=﹣2x+6 C.y=﹣2x﹣3 D.y=﹣2x﹣6
7.关于一次函数y=x+1,下列说法正确的是( )
A.图象经过第一、三、四象限 B.图象与y轴交于点(0,1)
C.函数值y随自变量x的增大而减小 D.当x>﹣1时,y<0
8.在同一平面直角坐标系中,函数和的图象可能是( )
A. B. C. D.
9.如图,直线y=﹣x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是( )
A.(2,5) B.(3,5) C.(5,2) D.(,2)
10.甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
二、填空题((11-14题每小题4分,15-16小题每题5分,共26分)
11.函数y=kx+3的图象经过点(2,5),则k= .
12.若直线向上平移3个单位长度后经过点,则的值为 .
13.一次函数与平行,且经过点(-3,4),则表达式为: .
14.如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 .
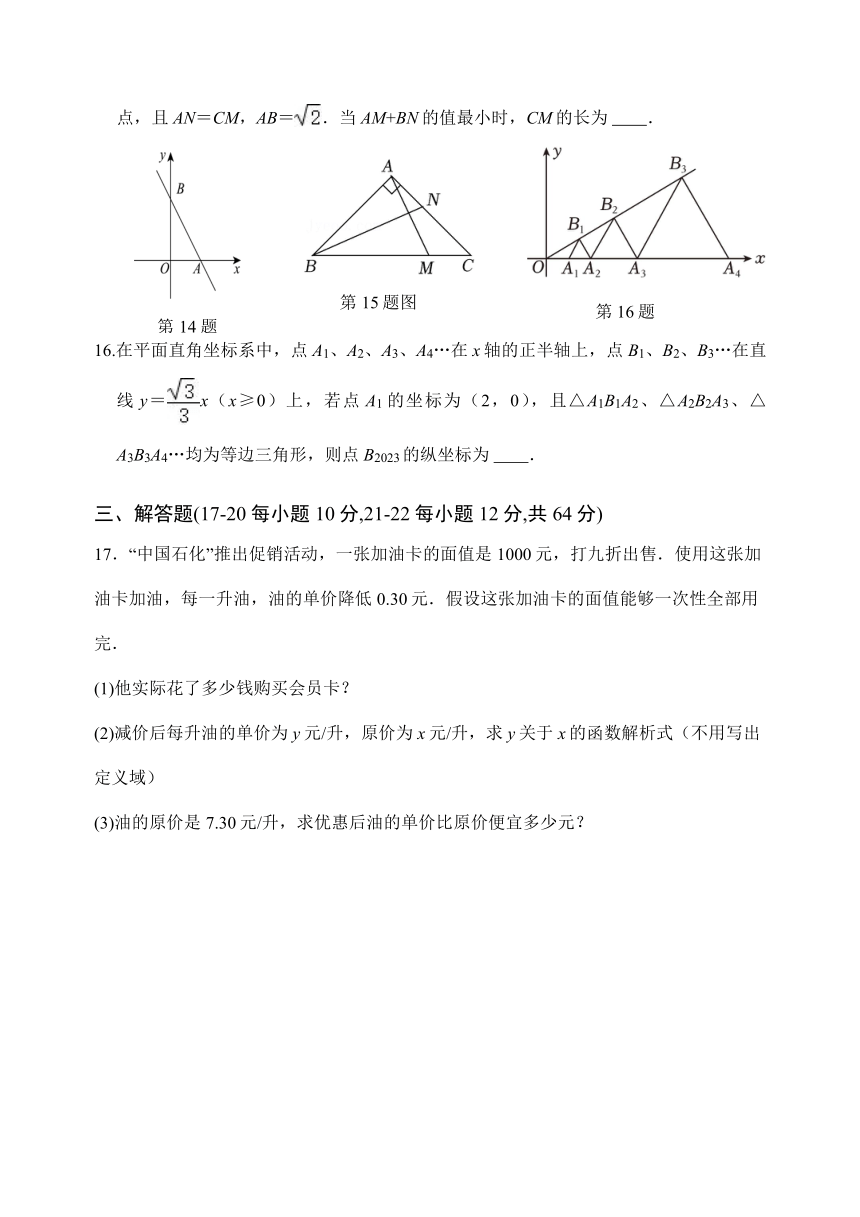
15.如图,在等腰直角三角形ABC中,∠BAC=90°,点M,N分别为BC,AC上的动点,且AN=CM,AB=.当AM+BN的值最小时,CM的长为 .
16.在平面直角坐标系中,点A1、A2、A3、A4…在x轴的正半轴上,点B1、B2、B3…在直线y=x(x≥0)上,若点A1的坐标为(2,0),且△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,则点B2023的纵坐标为 .
三、解答题(17-20每小题10分,21-22每小题12分,共64分)
17.“中国石化”推出促销活动,一张加油卡的面值是1000元,打九折出售.使用这张加油卡加油,每一升油,油的单价降低0.30元.假设这张加油卡的面值能够一次性全部用完.
(1)他实际花了多少钱购买会员卡?
(2)减价后每升油的单价为y元/升,原价为x元/升,求y关于x的函数解析式(不用写出定义域)
(3)油的原价是7.30元/升,求优惠后油的单价比原价便宜多少元?
18.在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.
(1)求该函数的解析式及点C的坐标;
(2)当x<3时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值.
19. 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用y1(元)与该水果的质量x(千克)之间的关系如图所示;在乙商店购买该水果的费用y2(元)与该水果的质量x(千克)之间的函数解析式为y2=10x(x≥0).
(1)求y1与x之间的函数解析式;
(2)现计划用600元购买该水果,选甲、乙哪家商店能购买该水果更多一些?
20.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售.经了解,每个乙种粽子的进价比每个甲种粽子的进价多2元,用1000元购进甲种粽子的个数与用1200元购进乙种粽子的个数相同.
(1)甲、乙两种粽子每个的进价分别是多少元?
(2)该超市计划购进这两种粽子共200个(两种都有),其中甲种粽子的个数不低于乙种粽子个数的2倍,若甲、乙两种粽子的售价分别为12元/个、15元/个,设购进甲种粽子m个,两种粽子全部售完时获得的利润为W元.
①求W与m的函数关系式,并求出m的取值范围;
②超市应如何进货才能获得最大利润,最大利润是多少元?
21.某市“共富工坊”问海借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二y关于x的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
22. 如图,在平面直角坐标系中, ABCD的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程x2﹣6x+8=0的两个根(OB>OC.请解答下列问题:
(1)求点B的坐标;
(2)若OD:OC=2:1,直线y=﹣x+b分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求tan∠MND的值;
(3)在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使△NPQ是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.
参考答案
一、选择题: 1.D 2. B 3. B 4. D 5.C
6. B 7. D 8.D 9.C 10.A
二、填空题:
11.1 12.5 13. 14. 1 15.
16.×22022
三、解答题:
17.(1)解:由题意知,(元),
答:实际花了900元购买会员卡;
(2)解:由题意知,,整理得,
∴y关于x的函数解析式为;
(3)解:当,则,
∵,
∴优惠后油的单价比原价便宜元.
18.解:(1)把点A(0,1),B(1,2)代入y=kx+b(k≠0)得:b=1,k+b=2,
解得:k=1,b=1,
∴该函数的解析式为y=x+1,
由题意知点C的纵坐标为4,
当y=x+1=4时, 解得:x=3,
∴C(3,4);
(2)由(1)知:当x=3时,y=x+1=4,
因为当x<3时,函数y=x+n的值大于函数y=x+1的值且小于4,
所以当y=x+n过点(3,4)时满足题意,
代入(3,4)得:4=×3+n,
解得:n=2.
19.解:(1)当0≤x≤5时,设y1与x之间的函数解析式为y1=kx(k≠0),把(5,75)代入解析式得:5k=75, 解得k=15,
∴y1=15x;
当x>5时,设y1与x之间的函数解析式为y1=mx+n(m≠0),
把(5,75)和(10,120)代入解析式得,解得,
∴y1=9x+30,
综上所述,y1与x之间的函数解析式为y1=;
(2)在甲商店购买:9x+30=600,
解得x=63,
∴在甲商店600元可以购买63千克水果;
在乙商店购买:10x=600, 解得x=60,
∴在乙商店600元可以购买60千克,
∵63>60,
∴在甲商店购买更多一些.
20. 解:(1)设每个甲种粽子的进价为x元,则每个乙种粽子的进价为(x+2)元,
根据题意得:=,
解得x=10,
经检验,x=10是原方程的根,
此时x+2=12,
答:每个甲种粽子的进价为10元,每个乙种粽子的进价为12元;
(2)①设购进甲种粽子m个,则购进乙种粽子(200﹣m)个,
根据题意得:W=(12﹣10)m+(15﹣12)(200﹣m)=2m+600﹣3m=﹣m+600,
∴W与m的函数关系式为W=﹣m+600;
甲种粽子的个数不低于乙种粽子个数的2倍,
∴m≥2(200﹣m),
解得m≥,
∴≤m<200(m为正整数);
②由①知,W=﹣m+600,﹣1<0,m为正整数,
∴当m=134时,W有最大值,最大值为466,
此时200﹣134=66,
∴购进甲种粽子134个,乙种粽子66个时利润最大,最大利润为466元.
21.(1)解:由图象可知交点坐标为,即员工生产30件产品时,两种方案付给的报酬一样多;
(2)由图象可得点,设方案二的函数表达式为,
把代入上式,得
解得
∴方案二的函数表达式为.
(3)若每月生产产品件数不足30件,则选择方案二;
若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;
若每月生产产品件数超过30件,则选择方案一.
22. 解:(1)由 x2﹣6x+8=0,得x1=4,x2=2,
∵OB>0C,
∴OB=4,0C=2,
∴B(﹣4,0);
(2)∵OD:OC=2:1,OC=2,
∴OD=4,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵M是AD中点,
∴MD=3,
∴M(﹣3,4),
将M(﹣3,4)代入y=﹣x+b,得:3+b=4,
解得:b=1,
在y=﹣x+b中,令x=0得y=1,令y=0得x=1,
∴E(1,0),F(0,1),
∴∠FEO=45°,
过点C作CH⊥EN于H,过点N作NK⊥BC于K,
∵∠DOC=∠NKC=90°,∠DCO=∠NCK,
∴△DOC∽△NKC,
∴DO:OC=NK:CK=2:1,
∴NK=EK=2CK,
∵CE=OC﹣OE=2﹣1=1,
∴CK=1,NK=2,
∴N(3,﹣2),
∴EN=2,EH===CH,
∴NH=EN﹣EH=,
∴tan∠MND===;
(3)存在点Q,使△NPQ是腰长为5的等腰三角形,理由如下:
由(2)知,N(3,﹣2),
设P(0,m),Q(t,﹣t+1),
∴PN2=9+(m+2)2,QN2=2(t﹣3)2,PQ2=t2+(m+t﹣1)2,
当PN=5时,9+(m+2)2=25,解得m=2或m=﹣6;
当QN=5时,2(t﹣3)2,解得t=;
①如图:
△P'NQ1,△PNQ2,△P'NQ2是腰长为5的等腰三角形,
结合图形可得Q1(﹣4,5),Q2(,);
②如图:
△P'NQ3,△P'NQ4,△PNQ4是边长为5的等腰三角形,
结合图形可得Q3(4,﹣3),Q4(,);
③如图:
△PQ5N,△P'Q5N是腰长为5的等腰三角形,此时Q5(,),
综上所述,腰长为5的等腰三角形NPQ共有8个,Q1(﹣4,5),Q2(,);Q3(4,﹣3),Q4(,).
2题图
5题图
3题图
第7题图
第16题
第15题图
第14题图
一、选择题(每小题3分,共30分)
1.下列各点在函数y=2x﹣1图象上的是( )
A.(﹣1,3) B.(0,1) C.(1,﹣1) D.(2,3)
2.已知一次函数的图象如图所示,则,的取值范围是( )
A., B., C., D.,
3.如图,直线y=ax+b(a≠0)过点A(0,3),B(4,0),则不等式ax+b>0的解集是( )
A.x>4 B.x<4 C.x>3 D.x<3
4.下列一次函数中,y随x的增大而减小的函数是( )
A.y=2x+1 B.y=x﹣4 C.y=2x D.y=﹣x+1
5.在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大 B.b<n
C.当x<2时,y1>y2 D.关于x,y的方程组的解为
6.在平面直角坐标系中,将正比例函数y=﹣2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=﹣2x+3 B.y=﹣2x+6 C.y=﹣2x﹣3 D.y=﹣2x﹣6
7.关于一次函数y=x+1,下列说法正确的是( )
A.图象经过第一、三、四象限 B.图象与y轴交于点(0,1)
C.函数值y随自变量x的增大而减小 D.当x>﹣1时,y<0
8.在同一平面直角坐标系中,函数和的图象可能是( )
A. B. C. D.
9.如图,直线y=﹣x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是( )
A.(2,5) B.(3,5) C.(5,2) D.(,2)
10.甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
二、填空题((11-14题每小题4分,15-16小题每题5分,共26分)
11.函数y=kx+3的图象经过点(2,5),则k= .
12.若直线向上平移3个单位长度后经过点,则的值为 .
13.一次函数与平行,且经过点(-3,4),则表达式为: .
14.如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 .
15.如图,在等腰直角三角形ABC中,∠BAC=90°,点M,N分别为BC,AC上的动点,且AN=CM,AB=.当AM+BN的值最小时,CM的长为 .
16.在平面直角坐标系中,点A1、A2、A3、A4…在x轴的正半轴上,点B1、B2、B3…在直线y=x(x≥0)上,若点A1的坐标为(2,0),且△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,则点B2023的纵坐标为 .
三、解答题(17-20每小题10分,21-22每小题12分,共64分)
17.“中国石化”推出促销活动,一张加油卡的面值是1000元,打九折出售.使用这张加油卡加油,每一升油,油的单价降低0.30元.假设这张加油卡的面值能够一次性全部用完.
(1)他实际花了多少钱购买会员卡?
(2)减价后每升油的单价为y元/升,原价为x元/升,求y关于x的函数解析式(不用写出定义域)
(3)油的原价是7.30元/升,求优惠后油的单价比原价便宜多少元?
18.在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.
(1)求该函数的解析式及点C的坐标;
(2)当x<3时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值.
19. 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用y1(元)与该水果的质量x(千克)之间的关系如图所示;在乙商店购买该水果的费用y2(元)与该水果的质量x(千克)之间的函数解析式为y2=10x(x≥0).
(1)求y1与x之间的函数解析式;
(2)现计划用600元购买该水果,选甲、乙哪家商店能购买该水果更多一些?
20.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售.经了解,每个乙种粽子的进价比每个甲种粽子的进价多2元,用1000元购进甲种粽子的个数与用1200元购进乙种粽子的个数相同.
(1)甲、乙两种粽子每个的进价分别是多少元?
(2)该超市计划购进这两种粽子共200个(两种都有),其中甲种粽子的个数不低于乙种粽子个数的2倍,若甲、乙两种粽子的售价分别为12元/个、15元/个,设购进甲种粽子m个,两种粽子全部售完时获得的利润为W元.
①求W与m的函数关系式,并求出m的取值范围;
②超市应如何进货才能获得最大利润,最大利润是多少元?
21.某市“共富工坊”问海借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.看图解答下列问题:
(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2)求方案二y关于x的函数表达式;
(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
22. 如图,在平面直角坐标系中, ABCD的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程x2﹣6x+8=0的两个根(OB>OC.请解答下列问题:
(1)求点B的坐标;
(2)若OD:OC=2:1,直线y=﹣x+b分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求tan∠MND的值;
(3)在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使△NPQ是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.
参考答案
一、选择题: 1.D 2. B 3. B 4. D 5.C
6. B 7. D 8.D 9.C 10.A
二、填空题:
11.1 12.5 13. 14. 1 15.
16.×22022
三、解答题:
17.(1)解:由题意知,(元),
答:实际花了900元购买会员卡;
(2)解:由题意知,,整理得,
∴y关于x的函数解析式为;
(3)解:当,则,
∵,
∴优惠后油的单价比原价便宜元.
18.解:(1)把点A(0,1),B(1,2)代入y=kx+b(k≠0)得:b=1,k+b=2,
解得:k=1,b=1,
∴该函数的解析式为y=x+1,
由题意知点C的纵坐标为4,
当y=x+1=4时, 解得:x=3,
∴C(3,4);
(2)由(1)知:当x=3时,y=x+1=4,
因为当x<3时,函数y=x+n的值大于函数y=x+1的值且小于4,
所以当y=x+n过点(3,4)时满足题意,
代入(3,4)得:4=×3+n,
解得:n=2.
19.解:(1)当0≤x≤5时,设y1与x之间的函数解析式为y1=kx(k≠0),把(5,75)代入解析式得:5k=75, 解得k=15,
∴y1=15x;
当x>5时,设y1与x之间的函数解析式为y1=mx+n(m≠0),
把(5,75)和(10,120)代入解析式得,解得,
∴y1=9x+30,
综上所述,y1与x之间的函数解析式为y1=;
(2)在甲商店购买:9x+30=600,
解得x=63,
∴在甲商店600元可以购买63千克水果;
在乙商店购买:10x=600, 解得x=60,
∴在乙商店600元可以购买60千克,
∵63>60,
∴在甲商店购买更多一些.
20. 解:(1)设每个甲种粽子的进价为x元,则每个乙种粽子的进价为(x+2)元,
根据题意得:=,
解得x=10,
经检验,x=10是原方程的根,
此时x+2=12,
答:每个甲种粽子的进价为10元,每个乙种粽子的进价为12元;
(2)①设购进甲种粽子m个,则购进乙种粽子(200﹣m)个,
根据题意得:W=(12﹣10)m+(15﹣12)(200﹣m)=2m+600﹣3m=﹣m+600,
∴W与m的函数关系式为W=﹣m+600;
甲种粽子的个数不低于乙种粽子个数的2倍,
∴m≥2(200﹣m),
解得m≥,
∴≤m<200(m为正整数);
②由①知,W=﹣m+600,﹣1<0,m为正整数,
∴当m=134时,W有最大值,最大值为466,
此时200﹣134=66,
∴购进甲种粽子134个,乙种粽子66个时利润最大,最大利润为466元.
21.(1)解:由图象可知交点坐标为,即员工生产30件产品时,两种方案付给的报酬一样多;
(2)由图象可得点,设方案二的函数表达式为,
把代入上式,得
解得
∴方案二的函数表达式为.
(3)若每月生产产品件数不足30件,则选择方案二;
若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;
若每月生产产品件数超过30件,则选择方案一.
22. 解:(1)由 x2﹣6x+8=0,得x1=4,x2=2,
∵OB>0C,
∴OB=4,0C=2,
∴B(﹣4,0);
(2)∵OD:OC=2:1,OC=2,
∴OD=4,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵M是AD中点,
∴MD=3,
∴M(﹣3,4),
将M(﹣3,4)代入y=﹣x+b,得:3+b=4,
解得:b=1,
在y=﹣x+b中,令x=0得y=1,令y=0得x=1,
∴E(1,0),F(0,1),
∴∠FEO=45°,
过点C作CH⊥EN于H,过点N作NK⊥BC于K,
∵∠DOC=∠NKC=90°,∠DCO=∠NCK,
∴△DOC∽△NKC,
∴DO:OC=NK:CK=2:1,
∴NK=EK=2CK,
∵CE=OC﹣OE=2﹣1=1,
∴CK=1,NK=2,
∴N(3,﹣2),
∴EN=2,EH===CH,
∴NH=EN﹣EH=,
∴tan∠MND===;
(3)存在点Q,使△NPQ是腰长为5的等腰三角形,理由如下:
由(2)知,N(3,﹣2),
设P(0,m),Q(t,﹣t+1),
∴PN2=9+(m+2)2,QN2=2(t﹣3)2,PQ2=t2+(m+t﹣1)2,
当PN=5时,9+(m+2)2=25,解得m=2或m=﹣6;
当QN=5时,2(t﹣3)2,解得t=;
①如图:
△P'NQ1,△PNQ2,△P'NQ2是腰长为5的等腰三角形,
结合图形可得Q1(﹣4,5),Q2(,);
②如图:
△P'NQ3,△P'NQ4,△PNQ4是边长为5的等腰三角形,
结合图形可得Q3(4,﹣3),Q4(,);
③如图:
△PQ5N,△P'Q5N是腰长为5的等腰三角形,此时Q5(,),
综上所述,腰长为5的等腰三角形NPQ共有8个,Q1(﹣4,5),Q2(,);Q3(4,﹣3),Q4(,).
2题图
5题图
3题图
第7题图
第16题
第15题图
第14题图
同课章节目录
