2025年九年级中考数学基础知识专项训练题6 反比例函数(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题6 反比例函数(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1012.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览


文档简介
2025中考数学基础知识专项训练题6 反比例函数
一、选择题:(每小题3分,共30分)
1.若反比例函数y=(k≠0)的图象经过点(2,﹣1),则k的值是( )
A.2 B.﹣2 C. D.
2. ( file: / / / G:\\2018中考解析\\中考数学(解析版)\\分类汇编\\cm )如图,平面直角坐标系中,O是坐标原点,点A是反比例函数图像上的一点,过点A分别作轴于点M,轴于直N,若四边形的面积为2.则k的值是( )
A.2 B. C.1 D.
3.已知正比例函数的图象经过点(1,﹣1),反比例函数的图象位于第一、第三象限,则一次函数y=ax+b的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,一次函数y=ax+b的图象与反比例函数的图象交于点A(2,3),B(m,﹣2),则不等式ax+b的解是( )
A.﹣3<x<0或x>2 B.x<﹣3或0<x<2
C.﹣2<x<0或x>2 D.﹣3<x<0或x>3
5.一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是( )
A.B. C.D.
6.已知蓄电池两端电压为定值,电流与成反比例函数关系.当时,,则当时,的值为( )
A. B. C. D.
7.某反比例函数图象上四个点的坐标分别为(﹣3,y1),(﹣2,3),(1,y2),(2,y3),则,y1,y2,y3的大小关系为( )
A.y2<y1<y3 B.y3<y2<y1 C.y2<y3<y1 D.y1<y3<y2
8.关于反比例函数,下列结论正确的是( )
A.图像位于第二、四象限 B.图像与坐标轴有公共点
C.图像所在的每一个象限内,随的增大而减小 D.图像经过点,则
9.如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,点D在AB上,且AD=AB,反比例函数y=(k>0)的图象经过点D及矩形OABC的对称中心M,连接OD,OM,DM.若△ODM的面积为3,则k的值为( )
A.2 B.3 C.4 D.5
10.如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(2,0),B(,1),△OA′B与△OAB关于直线OB对称,反比例函数y=(k>0,x>0)的图象与A′B交于点C.若A′C=BC,则k的值为( )
A.2 B. C. D.
填空题:(11-14小题每小题4分,15-16小题每题5分,共26分)
11.反比例函数y=的图象经过点A(m,),则反比例函数的表达式为 .
12.点,都在反比例函数的图象上,则 .(填“”或“”)
13.在平面直角坐标系xOy中,若反比例函数y=的图象位于第二、四象限,则k的取值范围是 .
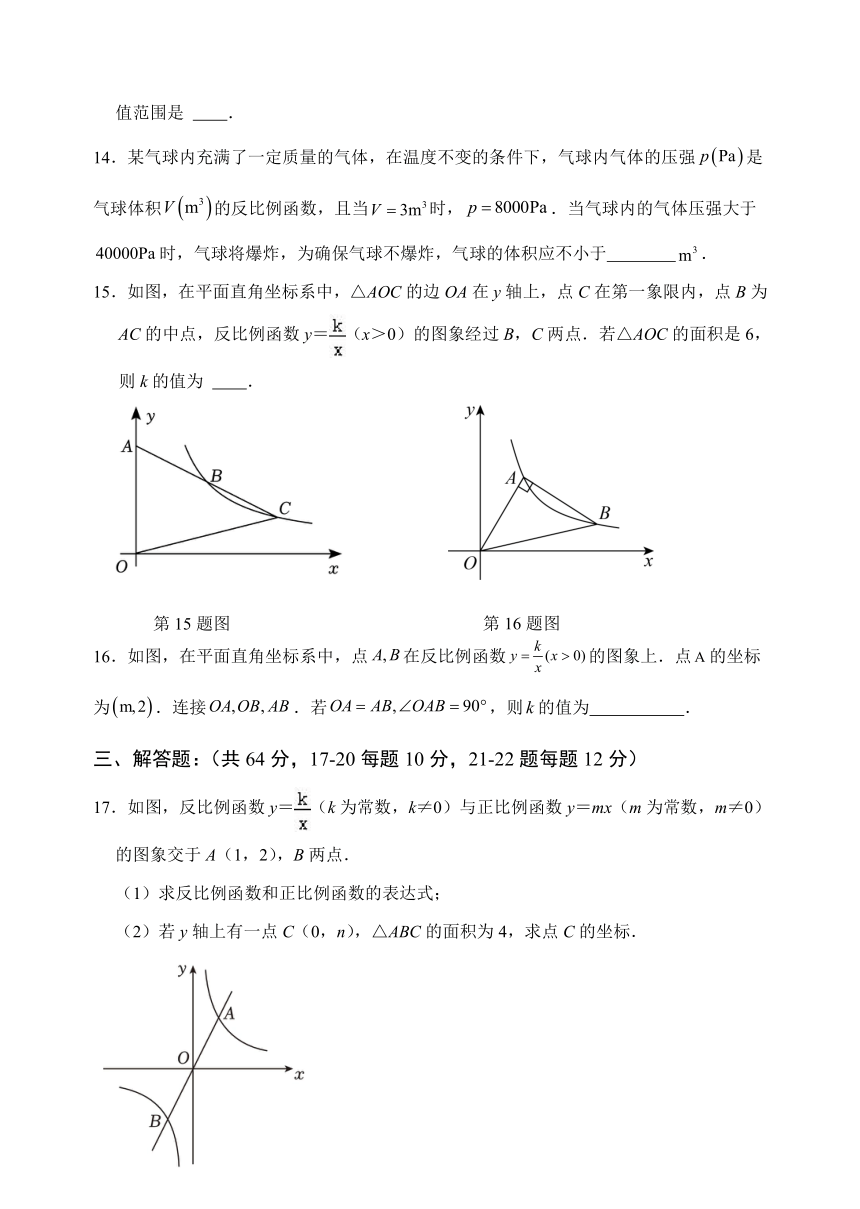
14.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时,.当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .
15.如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为 .
16.如图,在平面直角坐标系中,点在反比例函数的图象上.点的坐标为.连接.若,则的值为 .
三、解答题:(共64分,17-20每题10分,21-22题每题12分)
17.如图,反比例函数y=(k为常数,k≠0)与正比例函数y=mx(m为常数,m≠0)的图象交于A(1,2),B两点.
(1)求反比例函数和正比例函数的表达式;
(2)若y轴上有一点C(0,n),△ABC的面积为4,求点C的坐标.
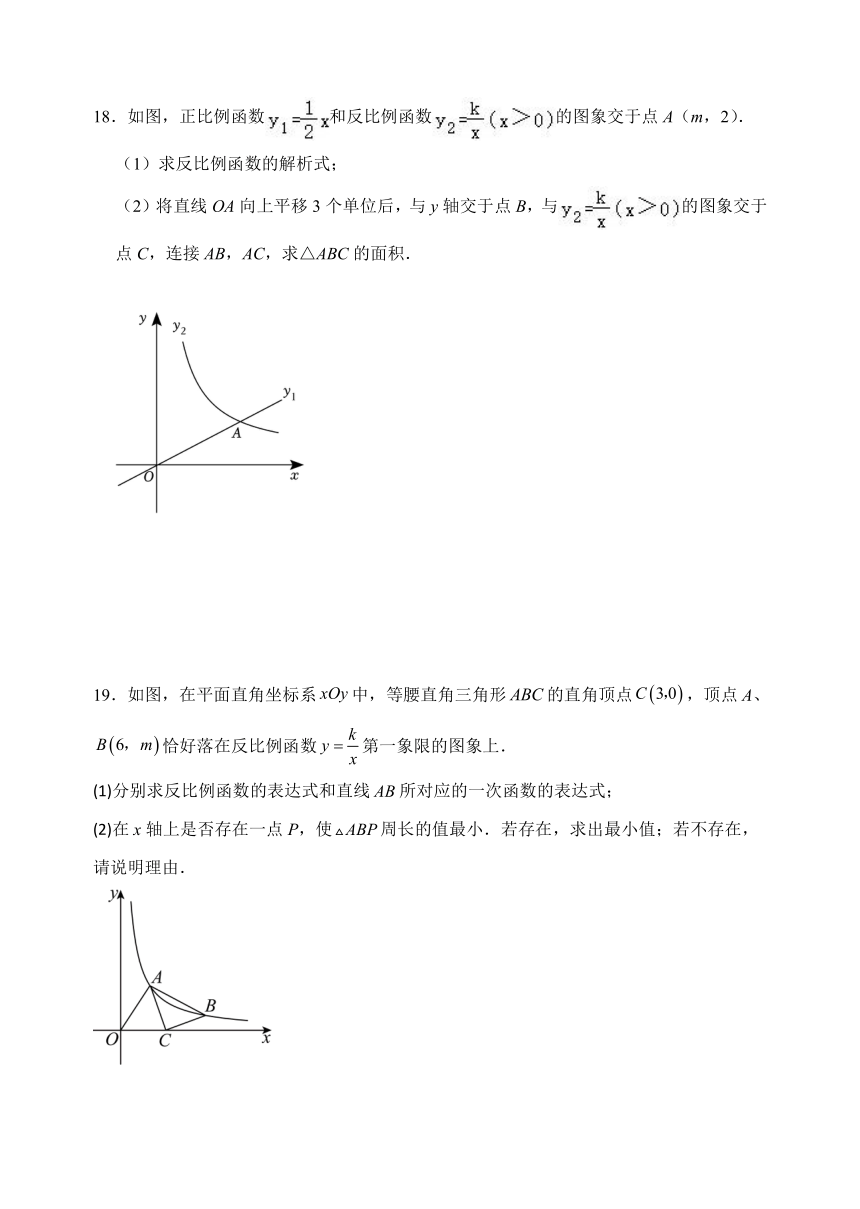
18.如图,正比例函数和反比例函数的图象交于点A(m,2).
(1)求反比例函数的解析式;
(2)将直线OA向上平移3个单位后,与y轴交于点B,与的图象交于点C,连接AB,AC,求△ABC的面积.
19.如图,在平面直角坐标系中,等腰直角三角形的直角顶点,顶点A、恰好落在反比例函数第一象限的图象上.
(1)分别求反比例函数的表达式和直线所对应的一次函数的表达式;
(2)在x轴上是否存在一点P,使周长的值最小.若存在,求出最小值;若不存在,请说明理由.
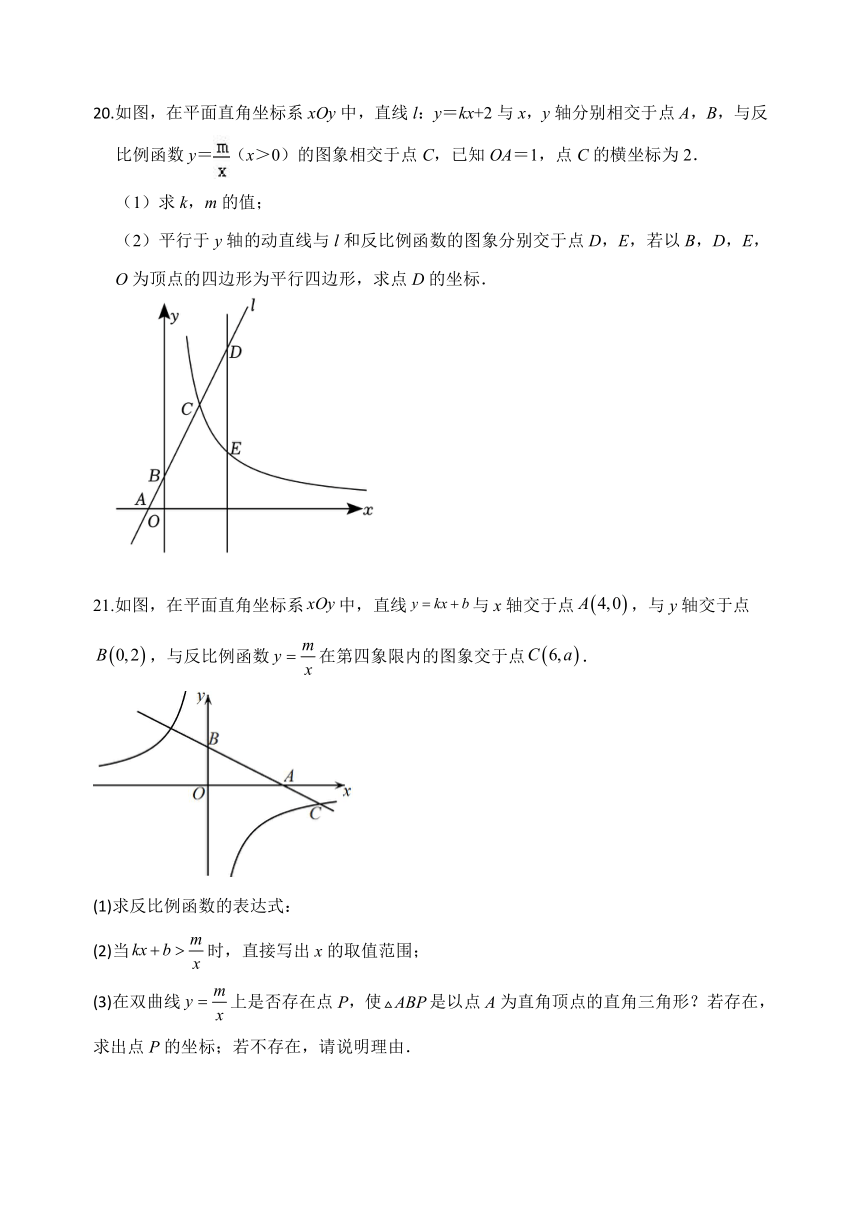
20.如图,在平面直角坐标系xOy中,直线l:y=kx+2与x,y轴分别相交于点A,B,与反比例函数y=(x>0)的图象相交于点C,已知OA=1,点C的横坐标为2.
(1)求k,m的值;
(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.
21.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点,与反比例函数在第四象限内的图象交于点.
(1)求反比例函数的表达式:
(2)当时,直接写出x的取值范围;
(3)在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
22.如图,在平面直角坐标系xOy中,一次函数图象y=﹣x+5与y轴交于点A,与反比例函数y=的图
象的一个交点为B(a,4),过点B作AB的垂线l.
(1)求点A的坐标及反比例函数的表达式;
(2)若点C在直线l上,且△ABC的面积为5,求点C的坐标;
(3)P是直线l上一点,连接PA,以P为位似中心画△PDE,使它与△PAB位似,相似比为m.若点D,E恰好都落在反比例函数图象上,求点P的坐标及m的值.
参考答案
一、选择题:(共30分)
1、B 2. A 3. C 4. A 5. D 6.D.7C 8 .C 9.C 10.A
二、填空题:(共24分)
11、y= ; 12、 ; 13.k<2 14、 ;15.4 16. .
三、解答题:(共46分)
17、解:(1)将点A(1,2)代入,得:k=2,
∴反比例函数的解析式为:,
将点A(1,2)代入y=mx,得:m=2,
∴正比例函数的解析式为:y=2x.
(2)解方程组,得:,,
∴点B的坐标为(﹣1,﹣2),
过点A,B分别作y轴的垂线,垂足分别为E,F,
∵A(1,2),B(﹣1,﹣2),C(0,n),
∴AE=BF=1,OC=|n|,
∵S△ABC=S△AOC+S△BOC=4,
∴,
即:|n|×1+|n×1=8,
∴|n|=4,
∴n=±4,
∴点C的坐标为(0,4)或(0,﹣4).
18、解:(1)把A(m,2)代入 得:
,
解得m=4,
∴A(4,2),
把A(4,2)代入 得: ,
解得k=8,
∴反比例函数的解析式为 ;
(2)过点C作CM⊥x轴于M,交AB于点N,如图:
将直线OA向上平移3个单位后,其函数解析式为 ,
当x=0时,y=3,
∴点B的坐标为(0,3),
设直线AB的函数解析式为y=mx+n,
将A(4,2),B(0,3)代入可得:
,
解得:,
∴直线AB的函数解析式为y=﹣x+3,
联立解析式得: 解得:,∴C点坐标为(2,4),
在y=﹣x+3中,当 x=2时,,
∴CN=4﹣=,
∴S△ABC=××4=3;
∴△ABC的面积为3.
19.解:(1)过点A作轴于点E,过点B作轴于点D,
则,
∵点,,
∴,
∴,
∵是等腰直角三角形,
∴,
∵,
∴,
∴,
∴,
∴,
∴点A的坐标是,
∵A、恰好落在反比例函数第一象限的图象上.
∴,
解得,
∴点A的坐标是,点B的坐标是,
∴,
∴反比例函数的解析式是,
设直线所对应的一次函数的表达式为,把点A和点B的坐标代入得,
,解得,
∴直线所对应的一次函数的表达式为,
(2)延长至点,使得,连接交x轴于点P,连接,
∴点A与点关于x轴对称,
∴,,
∵,
∴的最小值是的长度,
∵,即是定值,
∴此时的周长为最小,
设直线的解析式是,
则, 解得,
∴直线的解析式是,
当时,,解得,
即点P的坐标是,
此时,
综上可知,在x轴上存在一点,使周长的值最小,最小值是.
20、解:(1)∵OA=1,
∴点A的坐标为(﹣1,0),
则﹣k+2=0,
解得:k=2,
∴直线l的解析式为y=2x+2,
∵点C在直线l上,点C的横坐标为2,
∴点C的纵坐标为2×2+2=6,
∴点C的坐标为(2,6),
∴m=2×6=12;
(2)设点D的坐标为(n,2n+2),则点E的坐标为(n,),
∴DE=|2n+2﹣|,
∵OB∥DE,
∴当OB=DE时,以B,D,E,O为顶点的四边形为平行四边形,
∵直线y=2x+2与y轴交于点B,
∴OB=2,
∴|2n+2﹣|=2,
当2n+2﹣=2时,n1=,n2=﹣(舍去),
此时,点D的坐标为(,2+2),
当2n+2﹣=﹣2时,n1=﹣1,n2=﹣﹣1(舍去),
此时,点D的坐标为(﹣1,2),
综上所述:以B,D,E,O为顶点的四边形为平行四边形时,点D的坐标为(,2+2)或(﹣1,2).
21.解:(1)把,代入中得:,
∴,
∴直线的解析式为,
在中,当时,,
∴,
把代入中得:,
∴,
∴反比例函数的表达式;
(2)解:联立,解得或,
∴一次函数与反比例函数的两个交点坐标分别为,
∴由函数图象可知,当或时,一次函数图象在反比例函数图象上方,
∴当时,或;
(3)解:如图所示,设直线交y轴于点,
∵,,
∴,,,
∵是以点A为直角顶点的直角三角形,
∴,
∴,
∴,
解得,
∴,
同理可得直线的解析式为,
联立,解得或,
∴点P的坐标为或.
22、解:(1)令x=0,则y=﹣x+5=5,
∴点A的坐标为(0,5),
将B(a,4)代入y=﹣x+5得,4=﹣a+5,
∴a=1,
∴B(1,4),
将B(1,4)代入y=得,4=,
解得k=4,
∴反比例函数的表达式为y=;
(2)设直线l与y轴交于M,直线y=﹣x+5与x轴交于N,
令y=﹣x+5=0得,x=5,
∴N(5,0),
∴OA=ON=5,
∵∠AON=90°,
∴∠OAN=45°,
∵A(0,5),B(1,4),
∴=,
∵直线l是AB的垂线,即∠ABM=90°,∠OAN=45°,
∴,
∴M(0,3),
设直线l的解析式为y=k1x+b1,
将M(0,3),B(1,4)代入y=k1x+b1得,,
解得,
∴直线l的解析式为y=x+3,
设点C的坐标为(t,t+3),
∵ |xB﹣xC|=,
解得t=﹣4或t=6,
当t=﹣4时,t+3=﹣1,
当t=6时,t+3=9,
∴点C的坐标为(6,9)或(﹣4,﹣1);
(3)∵位似图形的对应点与位似中心三点共线,∴点B的对应点也在直线l上,不妨设为E点,则点A的对应点为D,
将直线l与双曲线的解析式联立方程组,
解得,或,
∴E(﹣4,﹣1),
画出图形如图所示,
∵△PAB∽△PDE,
∴∠PAB=∠PDE,
∴AB∥DE,
∴直线AB与直线DE的一次项系数相等,
设直线DE的解析式为y=﹣x+b2,
∴﹣1=﹣(﹣4)+b2,
∴b2=﹣5,
∴直线DE的解析式为y=﹣x﹣5,
∵点D在直线DE与双曲线的另一个交点,
∴解方程组得,或,
∴D(﹣1,﹣4),
则直线AD的解析式为y=9x+5,
解方程组得,,
∴P(﹣,),
∴,
,
∴m=.
9题图
10题图
第15题图
第16题图
PAGE
一、选择题:(每小题3分,共30分)
1.若反比例函数y=(k≠0)的图象经过点(2,﹣1),则k的值是( )
A.2 B.﹣2 C. D.
2. ( file: / / / G:\\2018中考解析\\中考数学(解析版)\\分类汇编\\cm )如图,平面直角坐标系中,O是坐标原点,点A是反比例函数图像上的一点,过点A分别作轴于点M,轴于直N,若四边形的面积为2.则k的值是( )
A.2 B. C.1 D.
3.已知正比例函数的图象经过点(1,﹣1),反比例函数的图象位于第一、第三象限,则一次函数y=ax+b的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,一次函数y=ax+b的图象与反比例函数的图象交于点A(2,3),B(m,﹣2),则不等式ax+b的解是( )
A.﹣3<x<0或x>2 B.x<﹣3或0<x<2
C.﹣2<x<0或x>2 D.﹣3<x<0或x>3
5.一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是( )
A.B. C.D.
6.已知蓄电池两端电压为定值,电流与成反比例函数关系.当时,,则当时,的值为( )
A. B. C. D.
7.某反比例函数图象上四个点的坐标分别为(﹣3,y1),(﹣2,3),(1,y2),(2,y3),则,y1,y2,y3的大小关系为( )
A.y2<y1<y3 B.y3<y2<y1 C.y2<y3<y1 D.y1<y3<y2
8.关于反比例函数,下列结论正确的是( )
A.图像位于第二、四象限 B.图像与坐标轴有公共点
C.图像所在的每一个象限内,随的增大而减小 D.图像经过点,则
9.如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,点D在AB上,且AD=AB,反比例函数y=(k>0)的图象经过点D及矩形OABC的对称中心M,连接OD,OM,DM.若△ODM的面积为3,则k的值为( )
A.2 B.3 C.4 D.5
10.如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(2,0),B(,1),△OA′B与△OAB关于直线OB对称,反比例函数y=(k>0,x>0)的图象与A′B交于点C.若A′C=BC,则k的值为( )
A.2 B. C. D.
填空题:(11-14小题每小题4分,15-16小题每题5分,共26分)
11.反比例函数y=的图象经过点A(m,),则反比例函数的表达式为 .
12.点,都在反比例函数的图象上,则 .(填“”或“”)
13.在平面直角坐标系xOy中,若反比例函数y=的图象位于第二、四象限,则k的取值范围是 .
14.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时,.当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .
15.如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为 .
16.如图,在平面直角坐标系中,点在反比例函数的图象上.点的坐标为.连接.若,则的值为 .
三、解答题:(共64分,17-20每题10分,21-22题每题12分)
17.如图,反比例函数y=(k为常数,k≠0)与正比例函数y=mx(m为常数,m≠0)的图象交于A(1,2),B两点.
(1)求反比例函数和正比例函数的表达式;
(2)若y轴上有一点C(0,n),△ABC的面积为4,求点C的坐标.
18.如图,正比例函数和反比例函数的图象交于点A(m,2).
(1)求反比例函数的解析式;
(2)将直线OA向上平移3个单位后,与y轴交于点B,与的图象交于点C,连接AB,AC,求△ABC的面积.
19.如图,在平面直角坐标系中,等腰直角三角形的直角顶点,顶点A、恰好落在反比例函数第一象限的图象上.
(1)分别求反比例函数的表达式和直线所对应的一次函数的表达式;
(2)在x轴上是否存在一点P,使周长的值最小.若存在,求出最小值;若不存在,请说明理由.
20.如图,在平面直角坐标系xOy中,直线l:y=kx+2与x,y轴分别相交于点A,B,与反比例函数y=(x>0)的图象相交于点C,已知OA=1,点C的横坐标为2.
(1)求k,m的值;
(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.
21.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点,与反比例函数在第四象限内的图象交于点.
(1)求反比例函数的表达式:
(2)当时,直接写出x的取值范围;
(3)在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
22.如图,在平面直角坐标系xOy中,一次函数图象y=﹣x+5与y轴交于点A,与反比例函数y=的图
象的一个交点为B(a,4),过点B作AB的垂线l.
(1)求点A的坐标及反比例函数的表达式;
(2)若点C在直线l上,且△ABC的面积为5,求点C的坐标;
(3)P是直线l上一点,连接PA,以P为位似中心画△PDE,使它与△PAB位似,相似比为m.若点D,E恰好都落在反比例函数图象上,求点P的坐标及m的值.
参考答案
一、选择题:(共30分)
1、B 2. A 3. C 4. A 5. D 6.D.7C 8 .C 9.C 10.A
二、填空题:(共24分)
11、y= ; 12、 ; 13.k<2 14、 ;15.4 16. .
三、解答题:(共46分)
17、解:(1)将点A(1,2)代入,得:k=2,
∴反比例函数的解析式为:,
将点A(1,2)代入y=mx,得:m=2,
∴正比例函数的解析式为:y=2x.
(2)解方程组,得:,,
∴点B的坐标为(﹣1,﹣2),
过点A,B分别作y轴的垂线,垂足分别为E,F,
∵A(1,2),B(﹣1,﹣2),C(0,n),
∴AE=BF=1,OC=|n|,
∵S△ABC=S△AOC+S△BOC=4,
∴,
即:|n|×1+|n×1=8,
∴|n|=4,
∴n=±4,
∴点C的坐标为(0,4)或(0,﹣4).
18、解:(1)把A(m,2)代入 得:
,
解得m=4,
∴A(4,2),
把A(4,2)代入 得: ,
解得k=8,
∴反比例函数的解析式为 ;
(2)过点C作CM⊥x轴于M,交AB于点N,如图:
将直线OA向上平移3个单位后,其函数解析式为 ,
当x=0时,y=3,
∴点B的坐标为(0,3),
设直线AB的函数解析式为y=mx+n,
将A(4,2),B(0,3)代入可得:
,
解得:,
∴直线AB的函数解析式为y=﹣x+3,
联立解析式得: 解得:,∴C点坐标为(2,4),
在y=﹣x+3中,当 x=2时,,
∴CN=4﹣=,
∴S△ABC=××4=3;
∴△ABC的面积为3.
19.解:(1)过点A作轴于点E,过点B作轴于点D,
则,
∵点,,
∴,
∴,
∵是等腰直角三角形,
∴,
∵,
∴,
∴,
∴,
∴,
∴点A的坐标是,
∵A、恰好落在反比例函数第一象限的图象上.
∴,
解得,
∴点A的坐标是,点B的坐标是,
∴,
∴反比例函数的解析式是,
设直线所对应的一次函数的表达式为,把点A和点B的坐标代入得,
,解得,
∴直线所对应的一次函数的表达式为,
(2)延长至点,使得,连接交x轴于点P,连接,
∴点A与点关于x轴对称,
∴,,
∵,
∴的最小值是的长度,
∵,即是定值,
∴此时的周长为最小,
设直线的解析式是,
则, 解得,
∴直线的解析式是,
当时,,解得,
即点P的坐标是,
此时,
综上可知,在x轴上存在一点,使周长的值最小,最小值是.
20、解:(1)∵OA=1,
∴点A的坐标为(﹣1,0),
则﹣k+2=0,
解得:k=2,
∴直线l的解析式为y=2x+2,
∵点C在直线l上,点C的横坐标为2,
∴点C的纵坐标为2×2+2=6,
∴点C的坐标为(2,6),
∴m=2×6=12;
(2)设点D的坐标为(n,2n+2),则点E的坐标为(n,),
∴DE=|2n+2﹣|,
∵OB∥DE,
∴当OB=DE时,以B,D,E,O为顶点的四边形为平行四边形,
∵直线y=2x+2与y轴交于点B,
∴OB=2,
∴|2n+2﹣|=2,
当2n+2﹣=2时,n1=,n2=﹣(舍去),
此时,点D的坐标为(,2+2),
当2n+2﹣=﹣2时,n1=﹣1,n2=﹣﹣1(舍去),
此时,点D的坐标为(﹣1,2),
综上所述:以B,D,E,O为顶点的四边形为平行四边形时,点D的坐标为(,2+2)或(﹣1,2).
21.解:(1)把,代入中得:,
∴,
∴直线的解析式为,
在中,当时,,
∴,
把代入中得:,
∴,
∴反比例函数的表达式;
(2)解:联立,解得或,
∴一次函数与反比例函数的两个交点坐标分别为,
∴由函数图象可知,当或时,一次函数图象在反比例函数图象上方,
∴当时,或;
(3)解:如图所示,设直线交y轴于点,
∵,,
∴,,,
∵是以点A为直角顶点的直角三角形,
∴,
∴,
∴,
解得,
∴,
同理可得直线的解析式为,
联立,解得或,
∴点P的坐标为或.
22、解:(1)令x=0,则y=﹣x+5=5,
∴点A的坐标为(0,5),
将B(a,4)代入y=﹣x+5得,4=﹣a+5,
∴a=1,
∴B(1,4),
将B(1,4)代入y=得,4=,
解得k=4,
∴反比例函数的表达式为y=;
(2)设直线l与y轴交于M,直线y=﹣x+5与x轴交于N,
令y=﹣x+5=0得,x=5,
∴N(5,0),
∴OA=ON=5,
∵∠AON=90°,
∴∠OAN=45°,
∵A(0,5),B(1,4),
∴=,
∵直线l是AB的垂线,即∠ABM=90°,∠OAN=45°,
∴,
∴M(0,3),
设直线l的解析式为y=k1x+b1,
将M(0,3),B(1,4)代入y=k1x+b1得,,
解得,
∴直线l的解析式为y=x+3,
设点C的坐标为(t,t+3),
∵ |xB﹣xC|=,
解得t=﹣4或t=6,
当t=﹣4时,t+3=﹣1,
当t=6时,t+3=9,
∴点C的坐标为(6,9)或(﹣4,﹣1);
(3)∵位似图形的对应点与位似中心三点共线,∴点B的对应点也在直线l上,不妨设为E点,则点A的对应点为D,
将直线l与双曲线的解析式联立方程组,
解得,或,
∴E(﹣4,﹣1),
画出图形如图所示,
∵△PAB∽△PDE,
∴∠PAB=∠PDE,
∴AB∥DE,
∴直线AB与直线DE的一次项系数相等,
设直线DE的解析式为y=﹣x+b2,
∴﹣1=﹣(﹣4)+b2,
∴b2=﹣5,
∴直线DE的解析式为y=﹣x﹣5,
∵点D在直线DE与双曲线的另一个交点,
∴解方程组得,或,
∴D(﹣1,﹣4),
则直线AD的解析式为y=9x+5,
解方程组得,,
∴P(﹣,),
∴,
,
∴m=.
9题图
10题图
第15题图
第16题图
PAGE
同课章节目录
