2025年九年级中考数学基础知识专项训练题11 圆(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题11 圆(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览


文档简介
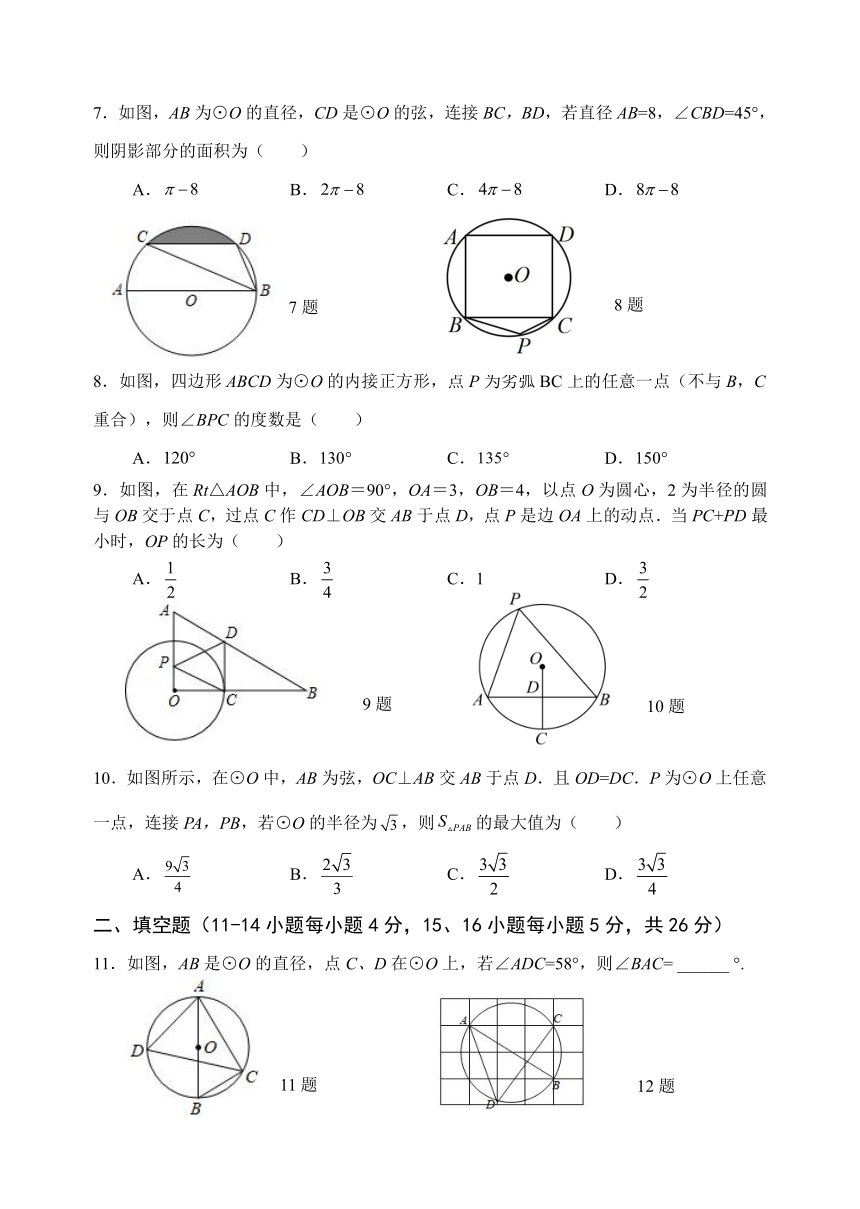
2025中考数学基础知识专项训练题11 圆
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.A,B,C是⊙O上的三点,若∠AOB=70°,则∠C的度数是( )
40° B.35° C.30° D.25°
2.如图,四边形内接于,若,则的度数为( )
A. B. C. D.
3.用直角尺检查某圆弧形工件,根据下列检查的结果,能判断该工件一定是半圆的是( )
A. B. C. D.
4.如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点,若AB=8,tan∠BAC=,则BC的长为( )
A. 8 B.7 C.10 D.6
5.如图,的半径为3,圆心O到的距离为2,则弦的长为( )
A.2 B. C. D.
6.下列命题中,真命题的个数是( )
①圆的每一条直径都是它的对称轴;②平分弦的直径必定垂直于这条弦;③在同圆或等圆中,相等的圆心角所对的弧相等;④在同圆中,相等的弦所对的弧相等.
A.4个 B.3个 C.2个 D.1个
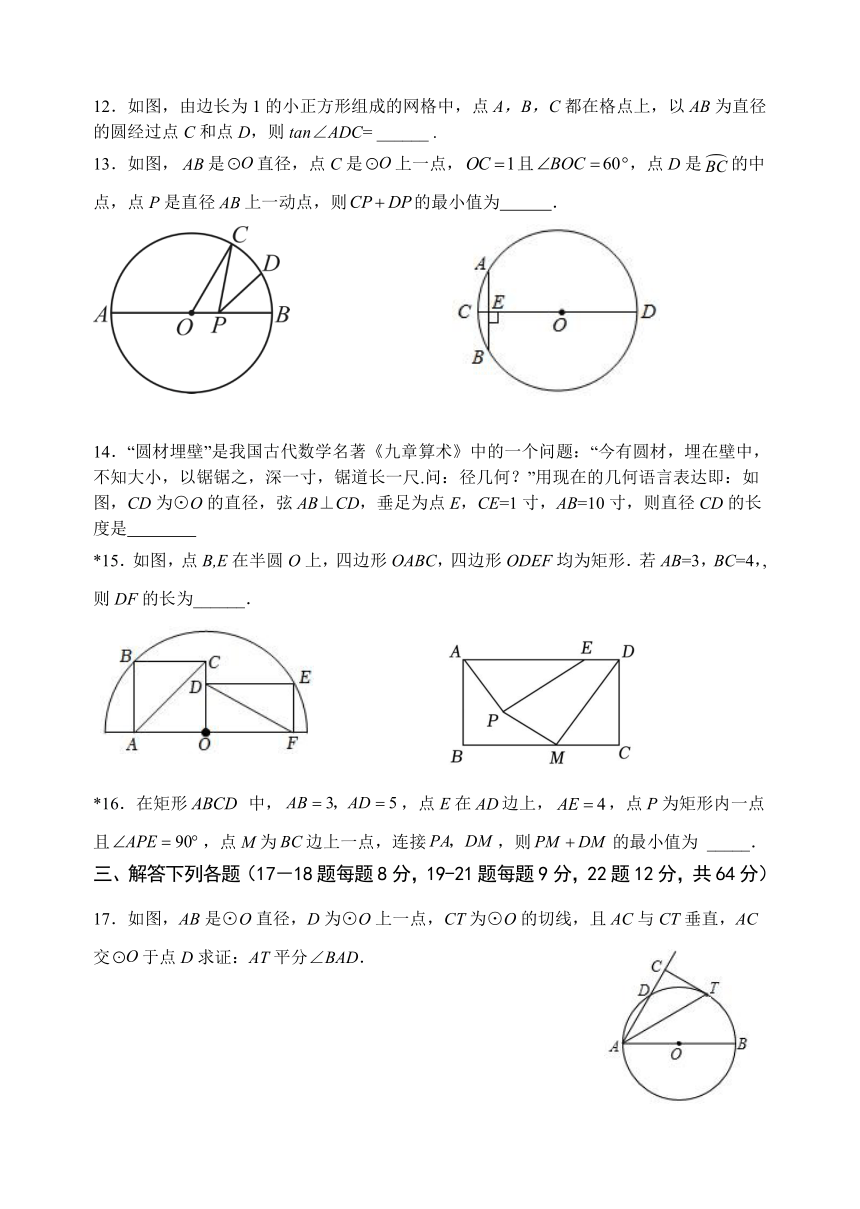
7.如图,AB为⊙O的直径,CD是⊙O的弦,连接BC,BD,若直径AB=8,∠CBD=45°,则阴影部分的面积为( )
A. B. C. D.
8.如图,四边形ABCD为⊙O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是( )
A. B. C. D.
9.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD最小时,OP的长为( )
A. B. C.1 D.
10.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为,则的最大值为( )
A. B. C. D.
二、填空题(11-14小题每小题4分,15、16小题每小题5分,共26分)
11.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC= ______ °.
12.如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC= ______ .
13.如图,是直径,点C是上一点,且,点D是的中点,点P是直径上一动点,则的最小值为 .
14.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是
*15.如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,,则DF的长为______.
*16.在矩形 中,,点E在边上,,点P为矩形内一点且,点M为边上一点,连接,则的最小值为 _____.
三、解答下列各题(17-18题每题8分,19-21题每题9分,22题12分,共64分)
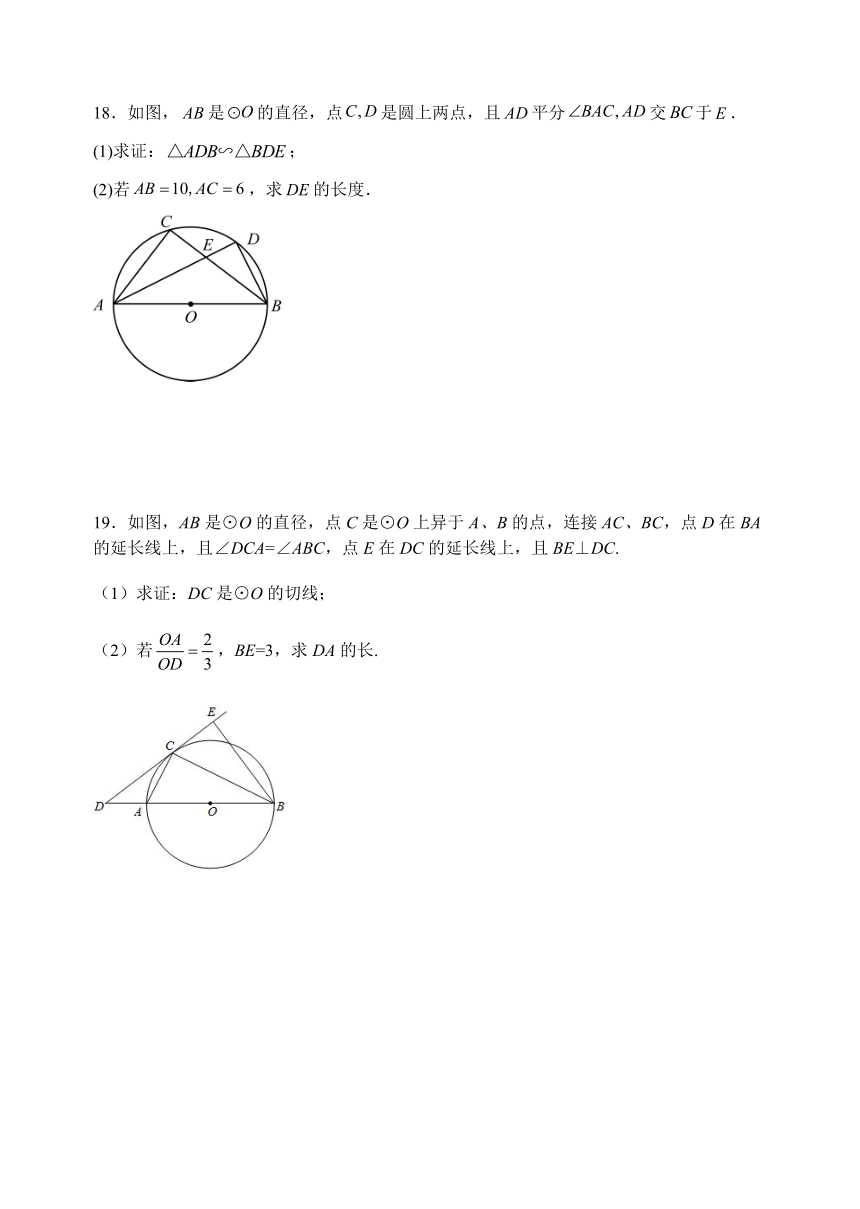
17.如图,AB是⊙O直径,D为⊙O上一点,CT为⊙O的切线,且AC与CT垂直,AC交于点D求证:AT平分∠BAD.
18.如图,是的直径,点是圆上两点,且平分交于.
(1)求证:;
(2)若,求的长度.
19.如图,AB是⊙O的直径,点C是⊙O上异于A、B的点,连接AC、BC,点D在BA的延长线上,且∠DCA=∠ABC,点E在DC的延长线上,且BE⊥DC.
(1)求证:DC是⊙O的切线;
(2)若,BE=3,求DA的长.
20.如图,在等腰三角形中,,以边为直径的与交于点,,垂足为,的延长线与的延长线交于点.
(1)求证:是的切线.
(2)若,,求的长.
21.如图,是的直径,是弦,D是的中点,与交于点E.F是延长线上的一点,且为的切线.
(1)试判断线段与的数量关系,并说明理由;
(2)连接,取的中点G,连接.若,求的长.
*22.如图,是的外接圆,为的直径,点I为的内心,连接并延长交于D点,连接并延长至E,使得,连接.
(1)求证:;
(2)求证:直线为的切线;
(3)若,求的长.
参考答案
一、1.B, 2. C, 3.B, 4.D, 5.B, 6.D, 7.B, 8.C, 9. B, 10.A.
二、11. 32 12. 13. 14.26 15.5 16.
三、17.连接,
∵为的切线,
∴,
∵,
∴,
∵,
∴,
∴,
∴平分
18.(1)证明:平分
∴∠DAC=∠DAB
,
,
又,
∴;
(2)解:连接,交于,
则,
,
,
,
,
,
由(1)知,
,即,
.
19.证明:连接OC,
∵OC=OB,
∴∠OCB=∠OBC,
∵∠ABC=∠DCA,
∴∠OCB=∠DCA,
又∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°,
∴∠DCA+∠ACO=90°,
即∠DCO=90°,
∴DC⊥OC,
∵OC是半径,
∴DC是⊙O的切线;
(2)解:∵,且OA=OB,
设OA=OB=2x,OD=3x,
∴DB=OD+OB=5x,
∴,
又∵BE⊥DC,DC⊥OC,
∴OC∥BE,
∴△DCO∽△DEB,
∴,
∵BE=3,∴OC=,
∴2x=,∴x=,
∴AD=OD-OA=x=,即AD的长为.
20.(1)证明:如图,连接,,
∵是直径,
∴,
又∵在中,,
∴,即是的中点,
∵,即是的中点,
∴是的中位线,
∴,
又∵,
∴,
∵为半径,
∴是的切线;
(2)解:∵,,,
∴,,
∵,
∴.
21.证明:如图,连接.
∵为的切线,
∴,
∵是的直径,D是的中点,
∴,
∴,
∵,
∴,
∴,
∴,
(2)解:过点G作于点H.
设,则,
在中,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵G为的中点,
∴,
∴,,
∴,
∴.
22.解(1)点I为的内心
又
∴
;
;
(2)连接,如图所示.
由(1)得:
则
∵为的直径,
∴
∴
,即
又为的直径
直线为的切线;
(3)为的直径
为直角三角形
不妨设
则有,
解得:
∴
过点I作交于点H,连接,如图所示.
∵点I为的内心,
∴点I到三边的距离相等,
∵,
∴,
∴
由(2)得:
同理可得:
故的长为.
2题
1题
5题
4题
7题
8题
10题
9题
11题
12题
PAGE
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.A,B,C是⊙O上的三点,若∠AOB=70°,则∠C的度数是( )
40° B.35° C.30° D.25°
2.如图,四边形内接于,若,则的度数为( )
A. B. C. D.
3.用直角尺检查某圆弧形工件,根据下列检查的结果,能判断该工件一定是半圆的是( )
A. B. C. D.
4.如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点,若AB=8,tan∠BAC=,则BC的长为( )
A. 8 B.7 C.10 D.6
5.如图,的半径为3,圆心O到的距离为2,则弦的长为( )
A.2 B. C. D.
6.下列命题中,真命题的个数是( )
①圆的每一条直径都是它的对称轴;②平分弦的直径必定垂直于这条弦;③在同圆或等圆中,相等的圆心角所对的弧相等;④在同圆中,相等的弦所对的弧相等.
A.4个 B.3个 C.2个 D.1个
7.如图,AB为⊙O的直径,CD是⊙O的弦,连接BC,BD,若直径AB=8,∠CBD=45°,则阴影部分的面积为( )
A. B. C. D.
8.如图,四边形ABCD为⊙O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是( )
A. B. C. D.
9.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD最小时,OP的长为( )
A. B. C.1 D.
10.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为,则的最大值为( )
A. B. C. D.
二、填空题(11-14小题每小题4分,15、16小题每小题5分,共26分)
11.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ADC=58°,则∠BAC= ______ °.
12.如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC= ______ .
13.如图,是直径,点C是上一点,且,点D是的中点,点P是直径上一动点,则的最小值为 .
14.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是
*15.如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,,则DF的长为______.
*16.在矩形 中,,点E在边上,,点P为矩形内一点且,点M为边上一点,连接,则的最小值为 _____.
三、解答下列各题(17-18题每题8分,19-21题每题9分,22题12分,共64分)
17.如图,AB是⊙O直径,D为⊙O上一点,CT为⊙O的切线,且AC与CT垂直,AC交于点D求证:AT平分∠BAD.
18.如图,是的直径,点是圆上两点,且平分交于.
(1)求证:;
(2)若,求的长度.
19.如图,AB是⊙O的直径,点C是⊙O上异于A、B的点,连接AC、BC,点D在BA的延长线上,且∠DCA=∠ABC,点E在DC的延长线上,且BE⊥DC.
(1)求证:DC是⊙O的切线;
(2)若,BE=3,求DA的长.
20.如图,在等腰三角形中,,以边为直径的与交于点,,垂足为,的延长线与的延长线交于点.
(1)求证:是的切线.
(2)若,,求的长.
21.如图,是的直径,是弦,D是的中点,与交于点E.F是延长线上的一点,且为的切线.
(1)试判断线段与的数量关系,并说明理由;
(2)连接,取的中点G,连接.若,求的长.
*22.如图,是的外接圆,为的直径,点I为的内心,连接并延长交于D点,连接并延长至E,使得,连接.
(1)求证:;
(2)求证:直线为的切线;
(3)若,求的长.
参考答案
一、1.B, 2. C, 3.B, 4.D, 5.B, 6.D, 7.B, 8.C, 9. B, 10.A.
二、11. 32 12. 13. 14.26 15.5 16.
三、17.连接,
∵为的切线,
∴,
∵,
∴,
∵,
∴,
∴,
∴平分
18.(1)证明:平分
∴∠DAC=∠DAB
,
,
又,
∴;
(2)解:连接,交于,
则,
,
,
,
,
,
由(1)知,
,即,
.
19.证明:连接OC,
∵OC=OB,
∴∠OCB=∠OBC,
∵∠ABC=∠DCA,
∴∠OCB=∠DCA,
又∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°,
∴∠DCA+∠ACO=90°,
即∠DCO=90°,
∴DC⊥OC,
∵OC是半径,
∴DC是⊙O的切线;
(2)解:∵,且OA=OB,
设OA=OB=2x,OD=3x,
∴DB=OD+OB=5x,
∴,
又∵BE⊥DC,DC⊥OC,
∴OC∥BE,
∴△DCO∽△DEB,
∴,
∵BE=3,∴OC=,
∴2x=,∴x=,
∴AD=OD-OA=x=,即AD的长为.
20.(1)证明:如图,连接,,
∵是直径,
∴,
又∵在中,,
∴,即是的中点,
∵,即是的中点,
∴是的中位线,
∴,
又∵,
∴,
∵为半径,
∴是的切线;
(2)解:∵,,,
∴,,
∵,
∴.
21.证明:如图,连接.
∵为的切线,
∴,
∵是的直径,D是的中点,
∴,
∴,
∵,
∴,
∴,
∴,
(2)解:过点G作于点H.
设,则,
在中,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵G为的中点,
∴,
∴,,
∴,
∴.
22.解(1)点I为的内心
又
∴
;
;
(2)连接,如图所示.
由(1)得:
则
∵为的直径,
∴
∴
,即
又为的直径
直线为的切线;
(3)为的直径
为直角三角形
不妨设
则有,
解得:
∴
过点I作交于点H,连接,如图所示.
∵点I为的内心,
∴点I到三边的距离相等,
∵,
∴,
∴
由(2)得:
同理可得:
故的长为.
2题
1题
5题
4题
7题
8题
10题
9题
11题
12题
PAGE
同课章节目录
