2025年九年级中考数学基础知识专项训练题12 命题与证明(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题12 命题与证明(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 18:38:05 | ||
图片预览




文档简介
2025中考数学基础知识专项训练题12 命题与证明
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一.选择题.(每题3分,共30分)
1.下列四个选项中不是命题的是( )
A.对顶角相等 B.过直线外—点作直线的平行线
C.三角形任意两边之和大于第三边 D.如果a=b , a = c,那么b = c
2.下列命题是假命题的是( )
A.任意一个三角形中,三角形两边的差小于第三边
B.三角形的中位线平行于三角形的第三边,并且等于第三边的一半
C.如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等
D.一组对边平行且相等的四边形是平行四边形
3.下列命题是真命题的是
A.同位角相等 B.菱形的四条边相等
C.正五边形是中心对称图形 D.单项式的次数是4
4.某同学的作业如下框,其中※处填的依据是( )
如图,已知直线.若,则.请完成下面的说理过程.解:已知,根据(内错角相等,两直线平行),得.再根据( ※ ),得.
A.两直线平行,内错角相等 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,同旁内角互补
5.下列命题中叙述正确的是( )
A.若方差s甲2>s乙2,则甲组数据的波动较小
B.直线外一点到这条直线的垂线段,叫做点到直线的距离
C.三角形三条中线的交点叫做三角形的内心
D.角的内部到角的两边的距离相等的点在角的平分线上
6.要说明命题“若a > b,则a2>b2”是假命题,下列所举的反例正确的是( )
A. a=2 , b =1 B.a= 2 , b =-3 C. a=2 , b =-1 D.a =-2 , b =-1
7.下列命题正确的是( )
A.在函数y=-x2中,当x>0时,y随x的增大而减小
B.若a<0,则1+a>1-a
C.垂直于半径的直线是圆的切线
D.各边相等的圆内接四边形是正方形
8.下列命题中,逆命题错误的是( )
A.两直线平行,同旁内角互补 B.对顶角相等
C.直角三角形的两个锐角互余 D.直角三角形两条直角边的平方和等于斜边的平方
9.用反证法证明"若≠,则a≠b"时,应首先假设( )
A.a>b B.a=b C.a 10.如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为和. 现给出下列命题:
①若,则;②若,则DF=2AD.那么,下面判断正确的是( )
A.①是真命题,②是真命题 B.①是真命题,②是假命题
C.①是假命题,②是真命题 D.①是假命题,②是假命题
二.填空题:(11-14小题,每小题4分,15、16小题每小题5分,共26分)
11.命题"对顶角相等”的逆命题是 .
12.命题“平行于同一直线的两直线平行”中:条件是 ,结论是 .
13.小明说︰命题“ =a”是假命题.若你想用一个实数a的值来举反例,则这个a的值可以是 .(写一个即可)
14.下列命题中,正确命题的个数为 .
①所有的正方形都相似 ②所有的菱形都相似
③边长相等的两个菱形都相似 ④对角线相等的两个矩形都相似
*15.如图,等边△ABC中,AB= 3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为 .
*16.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BC=,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△AB′C′,并使点C′落在AB边上,则点B所经过的路径长为 .(结果保留π)
三、解答题:(17-19题每题10分,20-21题每题12分,22题10分,共64分)
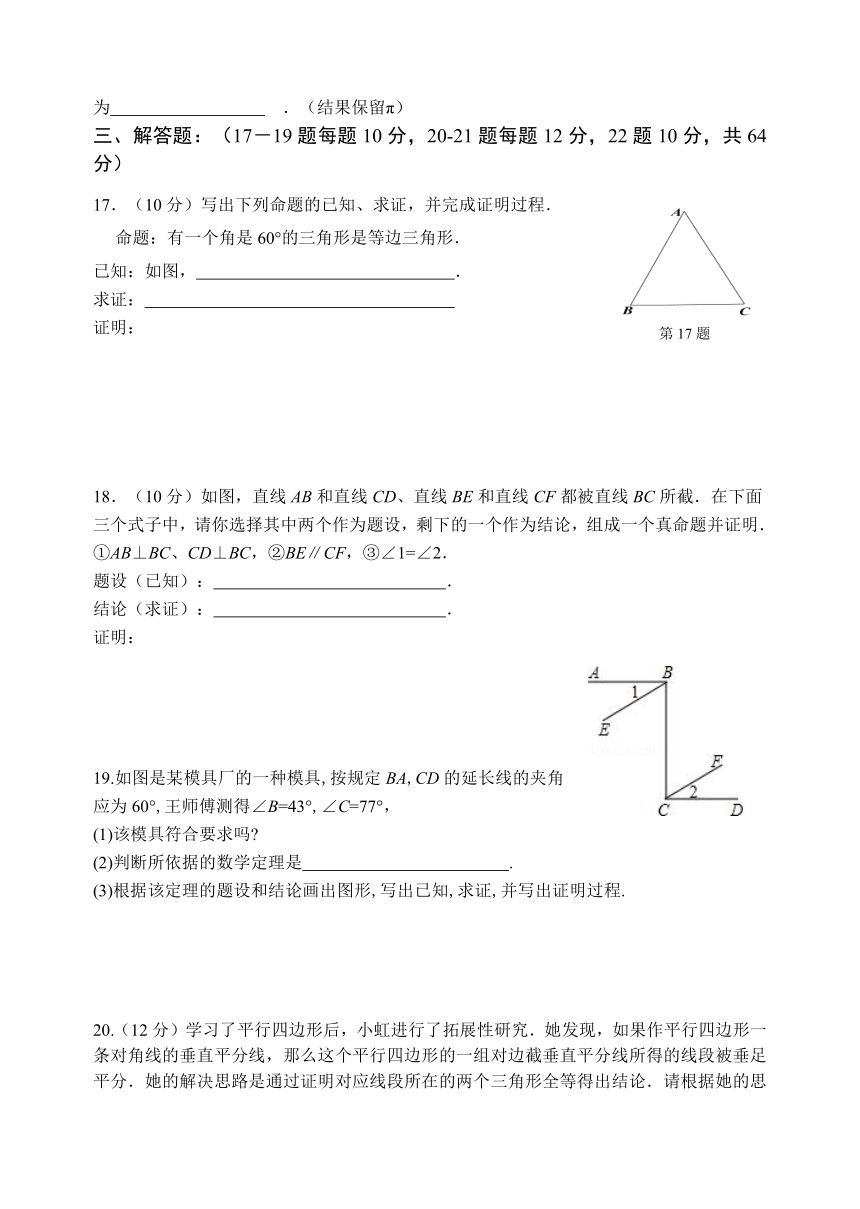
17.(10分)写出下列命题的已知、求证,并完成证明过程.
命题:有一个角是60°的三角形是等边三角形.
已知:如图, .
求证:
证明:
18.(10分)如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
题设(已知): .
结论(求证): .
证明:
19.如图是某模具厂的一种模具,按规定BA,CD的延长线的夹角应为60°,王师傅测得∠B=43°,∠C=77°,
(1)该模具符合要求吗
(2)判断所依据的数学定理是 .
(3)根据该定理的题设和结论画出图形,写出已知,求证,并写出证明过程.
20.(12分)学行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分.她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:用直尺和圆规,作AC的垂直平分线交DC于点E,交AB于点F,垂足为点O.(只保留作图痕迹)
已知:如图,四边形ABCD是平行四边形,AC是对角线,EF垂直平分AC,垂足为点O.求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB.
∴∠ECO= .
∵EF垂直平分AC,
∴ .
又∠EOC= ,
∴△COE≌△AOF(ASA).
∴OE=OF.
小虹再进一步研究发现,过平行四边形对角线AC中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:过平行四边形对角线中点的直线 .
21.(12分)如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD=CA,且∠D=30°.
(1)求证:CD是⊙O的切线.
(2)分别过A.B两点作直线CD的垂线,垂足分别为E.F两点,过C点作AB的垂线,垂足为点G.求证:CG2=AE BF.
*22.(10分)如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=-x+4与坐标轴的交点,点B的坐标为(-2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:①线段EF长度是否有最小值;②△BEF能否成为直角三角形.
小明尝试用“观察-猜想-验证-应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
参考答案
一、选择题
1.B 2.C 3.B 4.C 5.D 6.B 7.D 8.B 9.B 10.A
二、填空题
11.如果两个角相等,那么这两个角是对顶角;12. 两条直线同平行于同一条直线; 这两条直线互相平行;13. 1(答案不唯一);14.1;15.2;16.π.
三、解答题
17、已知:在△ABC中,AB=AC,∠B=60.
求证:△ABC是等边三角形. 证明:略
18.题设(已知): ①② .
结论(求证): ③ .
证明:∵AB⊥BC、CD⊥BC,
∴AB∥CD,
∴∠ABC=∠DCB,
又∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC﹣∠EBC=∠DCB﹣∠FCB,
∴∠1=∠2.
19.解:(1)∵BA,CD的延长线的夹角应为60°,
∴∠AED=60°,
∵∠B=43°,∠C=77°,
∴∠AED+∠B+∠C=180°.
符合三角形内角和定理即符合.
(2)三角形内角和等于180°.
(3)已知:△ABC,
求证:∠A+∠B+∠C=180°,
证明:如图,过点A做直线m,使m∥BC,
∵m∥BC,
∴∠2=∠4,同理∠3=∠5.
∵∠1,∠4,∠5组成平角,
∴∠1+∠4+∠5=180°.
∴∠1+∠2+∠3=180°,即三角形内角和等于180°.
20、解:(1);;;被一组对边截得的线段被对角线的中点平分.
21、(1)证明:连接OC,如右图所示,
∵CA=CD,且∠D=30°,
∴∠CAD=∠D=30°,
∵OA=OC,
∴∠CAD=∠ACO=30°,
∴∠COD=∠CAD+∠ACO=30°+30°=60°,
∴∠OCD=180°﹣∠D﹣∠COD=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)∵∠COB=60°,且OC=OB,
∴△OCB为等边三角形,
∴∠CBG=60°,
又∵CG⊥AD,
∴∠CGB=90°,
∴∠GCB=∠CGB﹣∠CBG=30°,
又∵∠GCD=60°,
∴CB是∠GCD的角平分线,
∵BF⊥CD,BG⊥CG,
∴BF=BG,
又∵BC=BC,
∴Rt△BCG≌Rt△BCF(HL),
∴CF=CG.
∵∠D=30°,AE⊥ED,∠E=90°,
∴∠EAD=60°,
又∵∠CAD=30°,
∴AC是∠EAG的角平分线,
∵CE⊥AE,CG⊥AB,
∴CE=CG,
∵∠E=∠BFC=90°,∠EAC=30°=∠BCF,
∴△AEC∽△CFB,
∴,即AE BF=CF CE,
又CE=CG,CF=CG,
∴AE BF=CG2.
22、解:(1)用描点法画出图形如图1,由图象可知函数类别为二次函数.
(2)如图2,过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,
则∠FGK=∠DHK=90°,
记FD交y轴于点K,
∵D点与F点关于y轴上的K点成中心对称,
∴KF=KD,
∵∠FKG=∠DKH,
∴Rt△FGK≌Rt△DHK(AAS),
∴FG=DH,
∵直线AC的解析式为y=﹣x+4,
∴x=0时,y=4,
∴A(0,4),
又∵B(﹣2,0),
设直线AB的解析式为y=kx+b,
∴,
解得,
∴直线AB的解析式为y=2x+4,
过点F作FR⊥x轴于点R,
∵D点的橫坐标为m,
∴F(﹣m,﹣2m+4),
∴ER=2m,FR=﹣2m+4,
∵EF2=FR2+ER2,
∴l=EF2=8m2﹣16m+16=8(m﹣1)2+8,
令﹣+4=0,得x=,
∴0≤m≤.
∴当m=1时,l的最小值为8,
∴EF的最小值为2.
(3)①∠FBE为定角,不可能为直角.
②∠BEF=90°时,E点与O点重合,D点与A点,F点重合,此时m=0.
③如图3,∠BFE=90°时,有BF2+EF2=BE2.
由(2)得EF2=8m2﹣16m+16,
又∵BR=﹣m+2,FR=﹣2m+4,
∴BF2=BR2+FR2=(﹣m+2)2+(﹣2m+4)2=5m2﹣20m+20,
又∵BE2=(m+2)2,
∴(5m2﹣20m+8)+(8m2﹣16m+16)2=(m+2)2,
化简得,3m2﹣10m+8=0,
解得m1=,m2=2(不合题意,舍去),
∴m=.
综合以上可得,当△BEF为直角三角形时,m=0或m=.
第16题图
第15题图
第17题
PAGE
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一.选择题.(每题3分,共30分)
1.下列四个选项中不是命题的是( )
A.对顶角相等 B.过直线外—点作直线的平行线
C.三角形任意两边之和大于第三边 D.如果a=b , a = c,那么b = c
2.下列命题是假命题的是( )
A.任意一个三角形中,三角形两边的差小于第三边
B.三角形的中位线平行于三角形的第三边,并且等于第三边的一半
C.如果一个角的两边分别平行于另一个角的两边,那么这两个角一定相等
D.一组对边平行且相等的四边形是平行四边形
3.下列命题是真命题的是
A.同位角相等 B.菱形的四条边相等
C.正五边形是中心对称图形 D.单项式的次数是4
4.某同学的作业如下框,其中※处填的依据是( )
如图,已知直线.若,则.请完成下面的说理过程.解:已知,根据(内错角相等,两直线平行),得.再根据( ※ ),得.
A.两直线平行,内错角相等 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,同旁内角互补
5.下列命题中叙述正确的是( )
A.若方差s甲2>s乙2,则甲组数据的波动较小
B.直线外一点到这条直线的垂线段,叫做点到直线的距离
C.三角形三条中线的交点叫做三角形的内心
D.角的内部到角的两边的距离相等的点在角的平分线上
6.要说明命题“若a > b,则a2>b2”是假命题,下列所举的反例正确的是( )
A. a=2 , b =1 B.a= 2 , b =-3 C. a=2 , b =-1 D.a =-2 , b =-1
7.下列命题正确的是( )
A.在函数y=-x2中,当x>0时,y随x的增大而减小
B.若a<0,则1+a>1-a
C.垂直于半径的直线是圆的切线
D.各边相等的圆内接四边形是正方形
8.下列命题中,逆命题错误的是( )
A.两直线平行,同旁内角互补 B.对顶角相等
C.直角三角形的两个锐角互余 D.直角三角形两条直角边的平方和等于斜边的平方
9.用反证法证明"若≠,则a≠b"时,应首先假设( )
A.a>b B.a=b C.a 10.如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为和. 现给出下列命题:
①若,则;②若,则DF=2AD.那么,下面判断正确的是( )
A.①是真命题,②是真命题 B.①是真命题,②是假命题
C.①是假命题,②是真命题 D.①是假命题,②是假命题
二.填空题:(11-14小题,每小题4分,15、16小题每小题5分,共26分)
11.命题"对顶角相等”的逆命题是 .
12.命题“平行于同一直线的两直线平行”中:条件是 ,结论是 .
13.小明说︰命题“ =a”是假命题.若你想用一个实数a的值来举反例,则这个a的值可以是 .(写一个即可)
14.下列命题中,正确命题的个数为 .
①所有的正方形都相似 ②所有的菱形都相似
③边长相等的两个菱形都相似 ④对角线相等的两个矩形都相似
*15.如图,等边△ABC中,AB= 3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为 .
*16.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BC=,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△AB′C′,并使点C′落在AB边上,则点B所经过的路径长为 .(结果保留π)
三、解答题:(17-19题每题10分,20-21题每题12分,22题10分,共64分)
17.(10分)写出下列命题的已知、求证,并完成证明过程.
命题:有一个角是60°的三角形是等边三角形.
已知:如图, .
求证:
证明:
18.(10分)如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
题设(已知): .
结论(求证): .
证明:
19.如图是某模具厂的一种模具,按规定BA,CD的延长线的夹角应为60°,王师傅测得∠B=43°,∠C=77°,
(1)该模具符合要求吗
(2)判断所依据的数学定理是 .
(3)根据该定理的题设和结论画出图形,写出已知,求证,并写出证明过程.
20.(12分)学行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分.她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:用直尺和圆规,作AC的垂直平分线交DC于点E,交AB于点F,垂足为点O.(只保留作图痕迹)
已知:如图,四边形ABCD是平行四边形,AC是对角线,EF垂直平分AC,垂足为点O.求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB.
∴∠ECO= .
∵EF垂直平分AC,
∴ .
又∠EOC= ,
∴△COE≌△AOF(ASA).
∴OE=OF.
小虹再进一步研究发现,过平行四边形对角线AC中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:过平行四边形对角线中点的直线 .
21.(12分)如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD=CA,且∠D=30°.
(1)求证:CD是⊙O的切线.
(2)分别过A.B两点作直线CD的垂线,垂足分别为E.F两点,过C点作AB的垂线,垂足为点G.求证:CG2=AE BF.
*22.(10分)如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=-x+4与坐标轴的交点,点B的坐标为(-2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:①线段EF长度是否有最小值;②△BEF能否成为直角三角形.
小明尝试用“观察-猜想-验证-应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
参考答案
一、选择题
1.B 2.C 3.B 4.C 5.D 6.B 7.D 8.B 9.B 10.A
二、填空题
11.如果两个角相等,那么这两个角是对顶角;12. 两条直线同平行于同一条直线; 这两条直线互相平行;13. 1(答案不唯一);14.1;15.2;16.π.
三、解答题
17、已知:在△ABC中,AB=AC,∠B=60.
求证:△ABC是等边三角形. 证明:略
18.题设(已知): ①② .
结论(求证): ③ .
证明:∵AB⊥BC、CD⊥BC,
∴AB∥CD,
∴∠ABC=∠DCB,
又∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC﹣∠EBC=∠DCB﹣∠FCB,
∴∠1=∠2.
19.解:(1)∵BA,CD的延长线的夹角应为60°,
∴∠AED=60°,
∵∠B=43°,∠C=77°,
∴∠AED+∠B+∠C=180°.
符合三角形内角和定理即符合.
(2)三角形内角和等于180°.
(3)已知:△ABC,
求证:∠A+∠B+∠C=180°,
证明:如图,过点A做直线m,使m∥BC,
∵m∥BC,
∴∠2=∠4,同理∠3=∠5.
∵∠1,∠4,∠5组成平角,
∴∠1+∠4+∠5=180°.
∴∠1+∠2+∠3=180°,即三角形内角和等于180°.
20、解:(1);;;被一组对边截得的线段被对角线的中点平分.
21、(1)证明:连接OC,如右图所示,
∵CA=CD,且∠D=30°,
∴∠CAD=∠D=30°,
∵OA=OC,
∴∠CAD=∠ACO=30°,
∴∠COD=∠CAD+∠ACO=30°+30°=60°,
∴∠OCD=180°﹣∠D﹣∠COD=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)∵∠COB=60°,且OC=OB,
∴△OCB为等边三角形,
∴∠CBG=60°,
又∵CG⊥AD,
∴∠CGB=90°,
∴∠GCB=∠CGB﹣∠CBG=30°,
又∵∠GCD=60°,
∴CB是∠GCD的角平分线,
∵BF⊥CD,BG⊥CG,
∴BF=BG,
又∵BC=BC,
∴Rt△BCG≌Rt△BCF(HL),
∴CF=CG.
∵∠D=30°,AE⊥ED,∠E=90°,
∴∠EAD=60°,
又∵∠CAD=30°,
∴AC是∠EAG的角平分线,
∵CE⊥AE,CG⊥AB,
∴CE=CG,
∵∠E=∠BFC=90°,∠EAC=30°=∠BCF,
∴△AEC∽△CFB,
∴,即AE BF=CF CE,
又CE=CG,CF=CG,
∴AE BF=CG2.
22、解:(1)用描点法画出图形如图1,由图象可知函数类别为二次函数.
(2)如图2,过点F,D分别作FG,DH垂直于y轴,垂足分别为G,H,
则∠FGK=∠DHK=90°,
记FD交y轴于点K,
∵D点与F点关于y轴上的K点成中心对称,
∴KF=KD,
∵∠FKG=∠DKH,
∴Rt△FGK≌Rt△DHK(AAS),
∴FG=DH,
∵直线AC的解析式为y=﹣x+4,
∴x=0时,y=4,
∴A(0,4),
又∵B(﹣2,0),
设直线AB的解析式为y=kx+b,
∴,
解得,
∴直线AB的解析式为y=2x+4,
过点F作FR⊥x轴于点R,
∵D点的橫坐标为m,
∴F(﹣m,﹣2m+4),
∴ER=2m,FR=﹣2m+4,
∵EF2=FR2+ER2,
∴l=EF2=8m2﹣16m+16=8(m﹣1)2+8,
令﹣+4=0,得x=,
∴0≤m≤.
∴当m=1时,l的最小值为8,
∴EF的最小值为2.
(3)①∠FBE为定角,不可能为直角.
②∠BEF=90°时,E点与O点重合,D点与A点,F点重合,此时m=0.
③如图3,∠BFE=90°时,有BF2+EF2=BE2.
由(2)得EF2=8m2﹣16m+16,
又∵BR=﹣m+2,FR=﹣2m+4,
∴BF2=BR2+FR2=(﹣m+2)2+(﹣2m+4)2=5m2﹣20m+20,
又∵BE2=(m+2)2,
∴(5m2﹣20m+8)+(8m2﹣16m+16)2=(m+2)2,
化简得,3m2﹣10m+8=0,
解得m1=,m2=2(不合题意,舍去),
∴m=.
综合以上可得,当△BEF为直角三角形时,m=0或m=.
第16题图
第15题图
第17题
PAGE
同课章节目录
