2025年九年级中考数学基础知识专项训练题13 视图与投影(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题13 视图与投影(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 739.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 18:38:51 | ||
图片预览

文档简介
2025中考数学基础知识专项训练题13 视图与投影
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
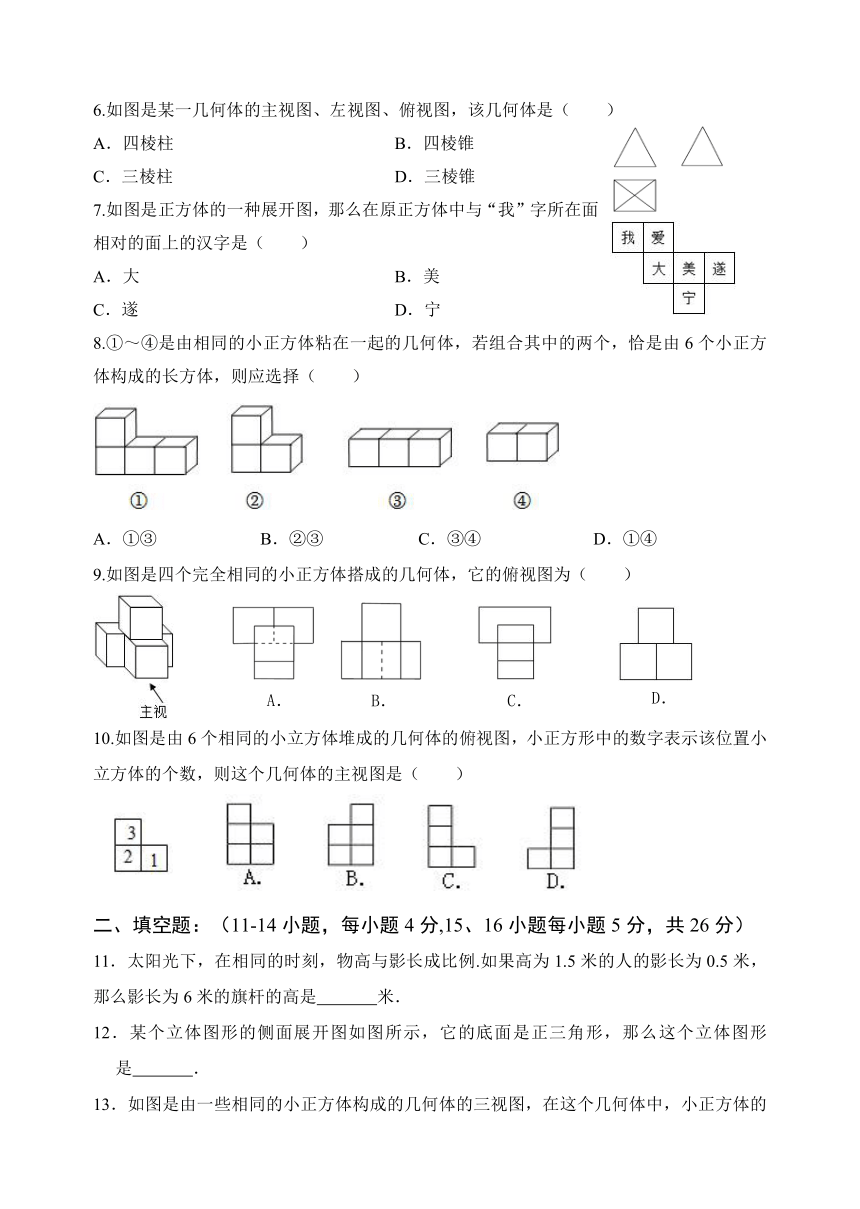
1.如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是( )
2.如图是由5个完全相同的小正方体组成的立体图形,其主视图是( )
3.下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
4.下列水平放置的几何体中,主视图是圆形的是( )
5.榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
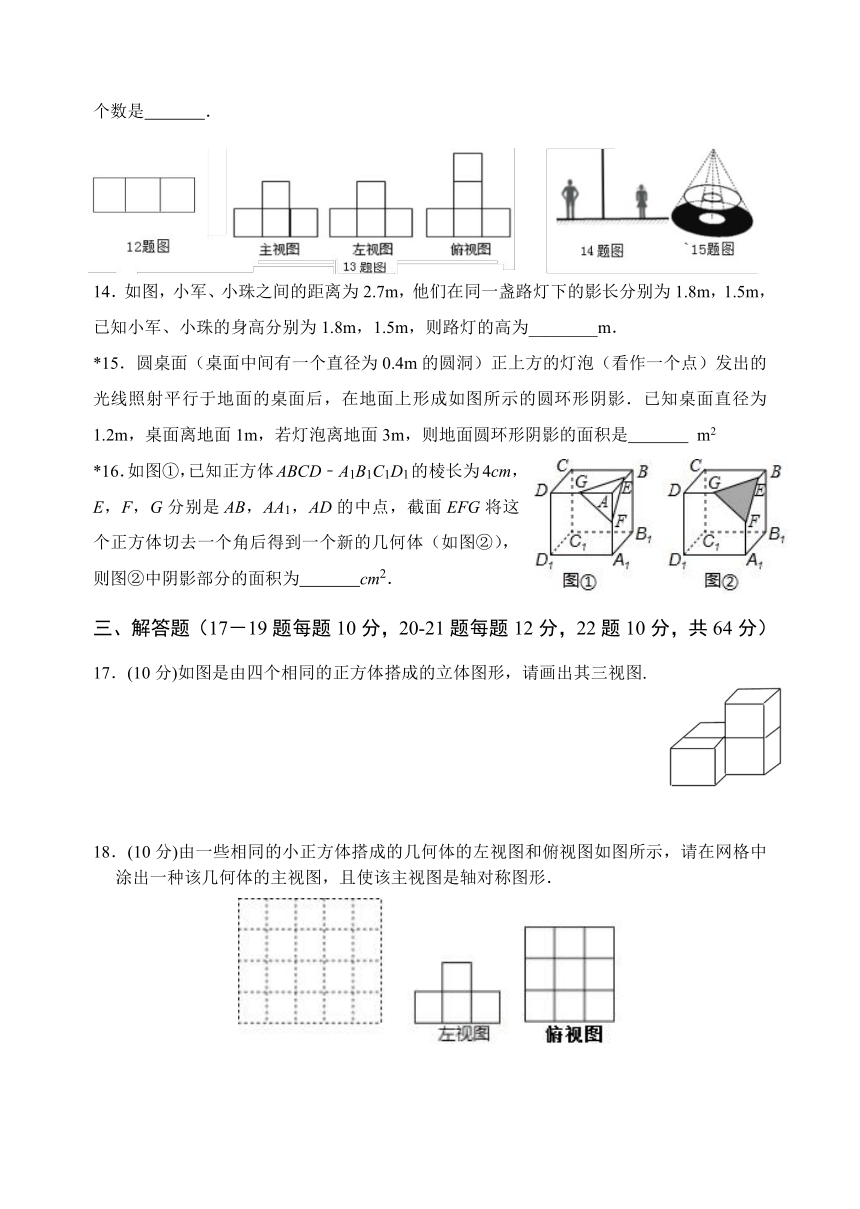
6.如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
7.如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美
C.遂 D.宁
8.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
9.如图是四个完全相同的小正方体搭成的几何体,它的俯视图为( )
10.如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
二、填空题:(11-14小题,每小题4分,15、16小题每小题5分,共26分)
11.太阳光下,在相同的时刻,物高与影长成比例.如果高为1.5米的人的影长为0.5米,那么影长为6米的旗杆的高是 米.
12.某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是 .
13.如图是由一些相同的小正方体构成的几何体的三视图,在这个几何体中,小正方体的个数是 .
14.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
*15.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是 m2
*16.如图①,已知正方体ABCD﹣A1B1C1D1的棱长为4cm,E,F,G分别是AB,AA1,AD的中点,截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),则图②中阴影部分的面积为 cm2.
三、解答题(17-19题每题10分,20-21题每题12分,22题10分,共64分)
17.(10分)如图是由四个相同的正方体搭成的立体图形,请画出其三视图.
18.(10分)由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
19.(10分)如图是某圆柱体果罐,它的主视图是边长为10cm的正方形,求果罐的侧面积.
20.(12分)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC =1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
21.(12分)爱成都,迎大运,成都东安湖体育公园是第13届世界大学生夏季运动会的主场馆所在地,如图为该公园内的大运会火炬塔.某校九年级学习兴趣小组想利用所学知识测量火炬塔塔身PQ的高度.如图所示,在阳光下,塔身PQ在地面上的影子为AP,某同学站在影子AP上的点B处时,他的影子刚好为AB,此时测得AB=2m,BP=34m,已知该同学的身高BC=1.72m,求火炬塔塔身PQ的高度.(结果精确到1m)
*22.(10分)如图,某测量工作人员的眼睛A与标杆顶端F、电视塔顶端E在同一直线上,已知此人眼睛A距地面1.6米,标杆FC为3.2米,且BC=1米,CD=5米,求电视塔的高ED.
参考答案
选择题
1.C 2.D 3.D 4.C 5.A 6.D 7.B 8.D 9.A 10.C
二、填空题
11.18米; 12.三棱柱; 13.6; 14.3; 15. 0.72π; 16.2.
三、解答题
17.解:
18. 如图:
19.解:∵果罐的主视图是边长为10cm的正方形,为圆柱体,
∴圆柱体的底面直径和高为10cm,
∴侧面积为=,
答:它的侧面积为100m2.
20.
21.
22.解:过A点作AH⊥ED,交FC于G,交ED于H.
由题意可得,四边形ABDH是矩形,
则AG=BC=1米,GH=CD=5米,AB=CG=DH=1.6米
FG=FC-CG=3.2-1.6=1.6米,AH=AG+GH=6米
∵FG∥DE
∴△AFG∽△AEH, ∴
∴,解得:EH=9.6米.
∴ED=9.6+1.6=11.2米.
答:电视塔高ED为11.2米。
A.
D.
C.
B.
PAGE
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是( )
2.如图是由5个完全相同的小正方体组成的立体图形,其主视图是( )
3.下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
4.下列水平放置的几何体中,主视图是圆形的是( )
5.榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
6.如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
7.如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美
C.遂 D.宁
8.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
9.如图是四个完全相同的小正方体搭成的几何体,它的俯视图为( )
10.如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
二、填空题:(11-14小题,每小题4分,15、16小题每小题5分,共26分)
11.太阳光下,在相同的时刻,物高与影长成比例.如果高为1.5米的人的影长为0.5米,那么影长为6米的旗杆的高是 米.
12.某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是 .
13.如图是由一些相同的小正方体构成的几何体的三视图,在这个几何体中,小正方体的个数是 .
14.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
*15.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是 m2
*16.如图①,已知正方体ABCD﹣A1B1C1D1的棱长为4cm,E,F,G分别是AB,AA1,AD的中点,截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),则图②中阴影部分的面积为 cm2.
三、解答题(17-19题每题10分,20-21题每题12分,22题10分,共64分)
17.(10分)如图是由四个相同的正方体搭成的立体图形,请画出其三视图.
18.(10分)由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
19.(10分)如图是某圆柱体果罐,它的主视图是边长为10cm的正方形,求果罐的侧面积.
20.(12分)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC =1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
21.(12分)爱成都,迎大运,成都东安湖体育公园是第13届世界大学生夏季运动会的主场馆所在地,如图为该公园内的大运会火炬塔.某校九年级学习兴趣小组想利用所学知识测量火炬塔塔身PQ的高度.如图所示,在阳光下,塔身PQ在地面上的影子为AP,某同学站在影子AP上的点B处时,他的影子刚好为AB,此时测得AB=2m,BP=34m,已知该同学的身高BC=1.72m,求火炬塔塔身PQ的高度.(结果精确到1m)
*22.(10分)如图,某测量工作人员的眼睛A与标杆顶端F、电视塔顶端E在同一直线上,已知此人眼睛A距地面1.6米,标杆FC为3.2米,且BC=1米,CD=5米,求电视塔的高ED.
参考答案
选择题
1.C 2.D 3.D 4.C 5.A 6.D 7.B 8.D 9.A 10.C
二、填空题
11.18米; 12.三棱柱; 13.6; 14.3; 15. 0.72π; 16.2.
三、解答题
17.解:
18. 如图:
19.解:∵果罐的主视图是边长为10cm的正方形,为圆柱体,
∴圆柱体的底面直径和高为10cm,
∴侧面积为=,
答:它的侧面积为100m2.
20.
21.
22.解:过A点作AH⊥ED,交FC于G,交ED于H.
由题意可得,四边形ABDH是矩形,
则AG=BC=1米,GH=CD=5米,AB=CG=DH=1.6米
FG=FC-CG=3.2-1.6=1.6米,AH=AG+GH=6米
∵FG∥DE
∴△AFG∽△AEH, ∴
∴,解得:EH=9.6米.
∴ED=9.6+1.6=11.2米.
答:电视塔高ED为11.2米。
A.
D.
C.
B.
PAGE
同课章节目录
