2025年九年级中考数学基础知识专项训练题14 图形的变换(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题14 图形的变换(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 856.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 18:39:26 | ||
图片预览


文档简介
2025中考数学基础知识专项训练题14 图形的变换
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题:(每小题3分,共30分)
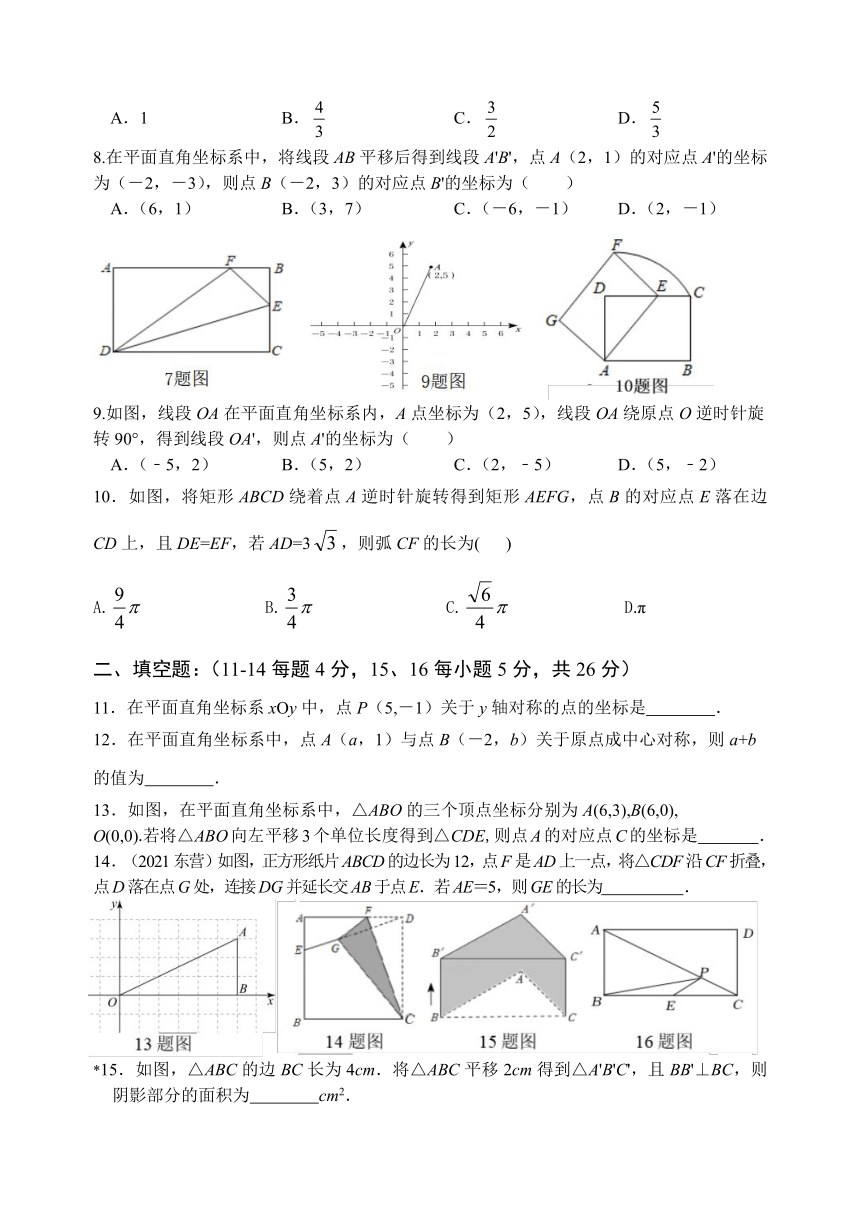
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
2.2022年2月第24届冬季奥林匹克运动会在我国北京成功举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列几何图形中,是轴对称图形但不是中心对称图形的是( )
A.梯形 B.等边三角形 C.平行四边形 D.矩形
4.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(﹣1)cm D.(2﹣1)cm
5.如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转得到△ADC,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于( )
A.80° B.85° C.90° D.95°
6.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A.中线 B.中位线 C.高线 D.角平分线
7.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
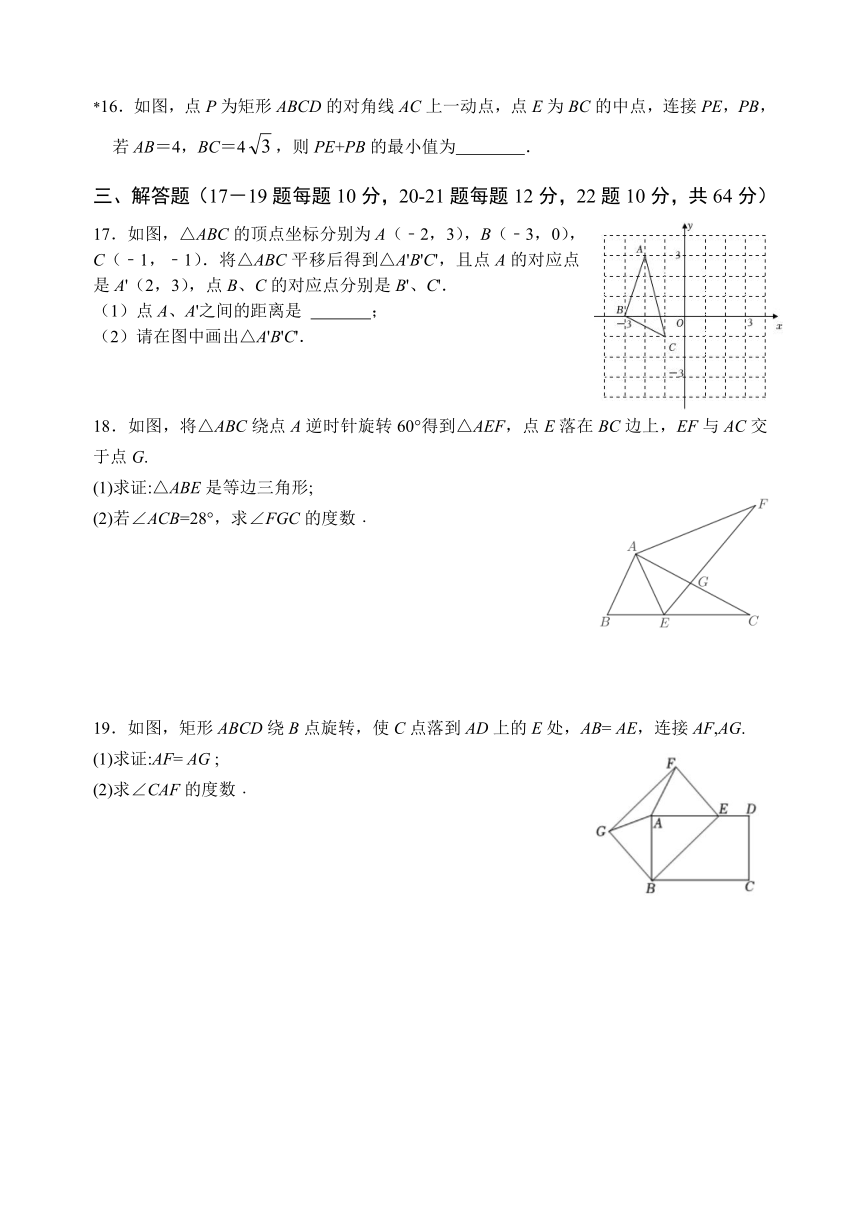
8.在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(-2,-3),则点B(-2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(-6,-1) D.(2,-1)
9.如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA',则点A'的坐标为( )
A.(﹣5,2) B.(5,2) C.(2,﹣5) D.(5,﹣2)
10.如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则弧CF的长为( )
A. B. C. D.π
二、填空题:(11-14每题4分,15、16每小题5分,共26分)
11.在平面直角坐标系xOy中,点P(5,-1)关于y轴对称的点的坐标是 .
12.在平面直角坐标系中,点A(a,1)与点B(-2,b)关于原点成中心对称,则a+b的值为 .
13.如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(6,3),B(6,0),
O(0,0).若将△ABO向左平移3个单位长度得到△CDE,则点A的对应点C的坐标是 .
14.(2021东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
*15.如图,△ABC的边BC长为4cm.将△ABC平移2cm得到△A'B'C',且BB'⊥BC,则阴影部分的面积为 cm2.
*16.如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=4,则PE+PB的最小值为 .
三、解答题(17-19题每题10分,20-21题每题12分,22题10分,共64分)
17.如图,△ABC的顶点坐标分别为A(﹣2,3),B(﹣3,0),C(﹣1,﹣1).将△ABC平移后得到△A'B'C',且点A的对应点是A'(2,3),点B、C的对应点分别是B'、C'.
(1)点A、A'之间的距离是 ;
(2)请在图中画出△A'B'C'.
18.如图,将△ABC绕点A逆时针旋转60°得到△AEF,点E落在BC边上,EF与AC交于点G.
(1)求证:△ABE是等边三角形;
(2)若∠ACB=28°,求∠FGC的度数﹒
19.如图,矩形ABCD绕B点旋转,使C点落到AD上的E处,AB= AE,连接AF,AG.
(1)求证:AF= AG ;
(2)求∠CAF的度数﹒
20.如图,将矩形ABCD沿对角线AC翻折,点B落在点F 处,FC交AD于E.
(1)求证:△AFE ≌ △CDE;
(2)若AB =4,BC =8,求图中阴影部分的面积.
21.如图,将边长为3的正方形ABCD沿直线EF折叠,使点B的对应点M落在边AD上(点M不与点A,D重合),点C落在点N处,MN与CD交于点P,折痕分别与边AB,CD交于点E,F,连接BM.
(1)求证:∠AMB=∠BMP;
(2)若DP=1,求MD的长.
*22.如图,在矩形ABCD中,AD=nAB(n>1),点E是AD边上一动点(点E不与A,D重合),连接BE,以BE为边在直线BE的右侧作矩形EBFG,使得矩形EBFG∽矩形ABCD,EG交直线CD于点H.
【尝试初探】
(1)在点E的运动过程中,△ABE与△DEH始终保持相似关系,请说明理由.
【深入探究】
(2)若n=2,随着E点位置的变化,H点的位置随之发生变化,当H是线段CD中点时,求tan∠ABE的值.
【拓展延伸】
(3)连接BH,FH,当△BFH是以FH为腰的等腰三角形时,求tan∠ABE的值(用含n的代数式表示).
参考答案
一、选择题
1.D 2. C 3. B 4.D 5. B 6.D 7.D 8. C 9. A 10. A
二、填空题
11.(-5,-1); 12. 1; 13.(3,3); 14. ; 15.8; 16.6.
三、解答题:
17.解:(1) 4 ;(2)如图
18.解:(1)证明:∵将△ABC绕点A逆时针旋转60得到△AEF, AB = AE,∠BAE=60°,
∴△ABE是等边三角形.
解:∵将△ABC绕点A逆时针旋转60得到△AEF,
∴∠BAE=∠CAF =60°,∠ACB=∠AFE=28°,
∵∠FGC是△AGF的外角,
∴∠FGC =∠CAF+∠AFE=88°.
19.解:
20.解:(1)∵四边形ABCD是矩形.
∴AB=CD,
由翻折得到:AB=AF,
∴AF=CD
∵
∴≌
设EF=DE=x,则AE=8-x.
在Rt△AEF中,由勾股定理得:
21.解:(1)证明:由翻折和正方形的性质可得,.
∴.
∴,即,
∵四边形是正方形,
∴.
∴.
∴.
(2)解:如图,延长交于点.
∵,
∴.
又∵,正方形边长为3,
∴
∴,
∴,,
设,则,
∴.
∵,即,
∴.
∴.
在中,,
∴.
解得:(舍),.
∴.
22.解(1)∵四边形EBFG和四边形ABCD是矩形,
∴∠A=∠BEG=∠D=90°,
∴∠ABE+∠AEB=∠AEB+∠DEH=90°,
∴∠DEH=∠ABE,
∴△ABE∽△DEH,
∴在点E的运动过程中,△ABE与△DEH始终保持相似关系;
(2)如图1,∵H是线段CD中点,∴DH=CH,
设DH=x,AE=a,则AB=2x,AD=4x,DE=4x﹣a,
由(1)知:△ABE∽△DEH,
∴=,即=,
∴2x2=4ax﹣a2,∴2x2﹣4ax+a2=0,
∴x==,
∵tan∠ABE==,
当x=时,tan∠ABE==,
当x=时,tan∠ABE==;
综上,tan∠ABE的值是.
(3)分两种情况:
①如图2,BH=FH,
设AB=x,AE=a,
∵四边形BEGF是矩形,
∴∠AEG=∠G=90°,BE=FG,
∴Rt△BEH≌Rt△FGH(HL),∴EH=GH,
∵矩形EBFG∽矩形ABCD,∴==n,∴=n,
∴=,
由(1)知:△ABE∽△DEH,∴==,∴=,∴nx=2a,
∴=,∴tan∠ABE===;
②如图3,BF=FH,
∵矩形EBFG∽矩形ABCD,
∴∠ABC=∠EBF=90°,=,
∴∠ABE=∠CBF,∴△ABE∽△CBF,
∴∠BCF=∠A=90°,∴D,C,F共线,
∵BF=FH,∴∠FBH=∠FHB,∵EG∥BF,
∴∠FBH=∠EHB,∴∠EHB=∠CHB,
∵BE⊥EH,BC⊥CH,∴BE=BC,
由①可知:AB=x,AE=a,BE=BC=nx,
由勾股定理得:AB2+AE2=BE2,
∴x2+a2=(nx)2,∴x=(负值舍),
∴tan∠ABE===,
综上,tan∠ABE的值是或.
PAGE
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题:(每小题3分,共30分)
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
2.2022年2月第24届冬季奥林匹克运动会在我国北京成功举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列几何图形中,是轴对称图形但不是中心对称图形的是( )
A.梯形 B.等边三角形 C.平行四边形 D.矩形
4.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(﹣1)cm D.(2﹣1)cm
5.如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转得到△ADC,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于( )
A.80° B.85° C.90° D.95°
6.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A.中线 B.中位线 C.高线 D.角平分线
7.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
8.在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(-2,-3),则点B(-2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(-6,-1) D.(2,-1)
9.如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA',则点A'的坐标为( )
A.(﹣5,2) B.(5,2) C.(2,﹣5) D.(5,﹣2)
10.如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则弧CF的长为( )
A. B. C. D.π
二、填空题:(11-14每题4分,15、16每小题5分,共26分)
11.在平面直角坐标系xOy中,点P(5,-1)关于y轴对称的点的坐标是 .
12.在平面直角坐标系中,点A(a,1)与点B(-2,b)关于原点成中心对称,则a+b的值为 .
13.如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(6,3),B(6,0),
O(0,0).若将△ABO向左平移3个单位长度得到△CDE,则点A的对应点C的坐标是 .
14.(2021东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
*15.如图,△ABC的边BC长为4cm.将△ABC平移2cm得到△A'B'C',且BB'⊥BC,则阴影部分的面积为 cm2.
*16.如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=4,则PE+PB的最小值为 .
三、解答题(17-19题每题10分,20-21题每题12分,22题10分,共64分)
17.如图,△ABC的顶点坐标分别为A(﹣2,3),B(﹣3,0),C(﹣1,﹣1).将△ABC平移后得到△A'B'C',且点A的对应点是A'(2,3),点B、C的对应点分别是B'、C'.
(1)点A、A'之间的距离是 ;
(2)请在图中画出△A'B'C'.
18.如图,将△ABC绕点A逆时针旋转60°得到△AEF,点E落在BC边上,EF与AC交于点G.
(1)求证:△ABE是等边三角形;
(2)若∠ACB=28°,求∠FGC的度数﹒
19.如图,矩形ABCD绕B点旋转,使C点落到AD上的E处,AB= AE,连接AF,AG.
(1)求证:AF= AG ;
(2)求∠CAF的度数﹒
20.如图,将矩形ABCD沿对角线AC翻折,点B落在点F 处,FC交AD于E.
(1)求证:△AFE ≌ △CDE;
(2)若AB =4,BC =8,求图中阴影部分的面积.
21.如图,将边长为3的正方形ABCD沿直线EF折叠,使点B的对应点M落在边AD上(点M不与点A,D重合),点C落在点N处,MN与CD交于点P,折痕分别与边AB,CD交于点E,F,连接BM.
(1)求证:∠AMB=∠BMP;
(2)若DP=1,求MD的长.
*22.如图,在矩形ABCD中,AD=nAB(n>1),点E是AD边上一动点(点E不与A,D重合),连接BE,以BE为边在直线BE的右侧作矩形EBFG,使得矩形EBFG∽矩形ABCD,EG交直线CD于点H.
【尝试初探】
(1)在点E的运动过程中,△ABE与△DEH始终保持相似关系,请说明理由.
【深入探究】
(2)若n=2,随着E点位置的变化,H点的位置随之发生变化,当H是线段CD中点时,求tan∠ABE的值.
【拓展延伸】
(3)连接BH,FH,当△BFH是以FH为腰的等腰三角形时,求tan∠ABE的值(用含n的代数式表示).
参考答案
一、选择题
1.D 2. C 3. B 4.D 5. B 6.D 7.D 8. C 9. A 10. A
二、填空题
11.(-5,-1); 12. 1; 13.(3,3); 14. ; 15.8; 16.6.
三、解答题:
17.解:(1) 4 ;(2)如图
18.解:(1)证明:∵将△ABC绕点A逆时针旋转60得到△AEF, AB = AE,∠BAE=60°,
∴△ABE是等边三角形.
解:∵将△ABC绕点A逆时针旋转60得到△AEF,
∴∠BAE=∠CAF =60°,∠ACB=∠AFE=28°,
∵∠FGC是△AGF的外角,
∴∠FGC =∠CAF+∠AFE=88°.
19.解:
20.解:(1)∵四边形ABCD是矩形.
∴AB=CD,
由翻折得到:AB=AF,
∴AF=CD
∵
∴≌
设EF=DE=x,则AE=8-x.
在Rt△AEF中,由勾股定理得:
21.解:(1)证明:由翻折和正方形的性质可得,.
∴.
∴,即,
∵四边形是正方形,
∴.
∴.
∴.
(2)解:如图,延长交于点.
∵,
∴.
又∵,正方形边长为3,
∴
∴,
∴,,
设,则,
∴.
∵,即,
∴.
∴.
在中,,
∴.
解得:(舍),.
∴.
22.解(1)∵四边形EBFG和四边形ABCD是矩形,
∴∠A=∠BEG=∠D=90°,
∴∠ABE+∠AEB=∠AEB+∠DEH=90°,
∴∠DEH=∠ABE,
∴△ABE∽△DEH,
∴在点E的运动过程中,△ABE与△DEH始终保持相似关系;
(2)如图1,∵H是线段CD中点,∴DH=CH,
设DH=x,AE=a,则AB=2x,AD=4x,DE=4x﹣a,
由(1)知:△ABE∽△DEH,
∴=,即=,
∴2x2=4ax﹣a2,∴2x2﹣4ax+a2=0,
∴x==,
∵tan∠ABE==,
当x=时,tan∠ABE==,
当x=时,tan∠ABE==;
综上,tan∠ABE的值是.
(3)分两种情况:
①如图2,BH=FH,
设AB=x,AE=a,
∵四边形BEGF是矩形,
∴∠AEG=∠G=90°,BE=FG,
∴Rt△BEH≌Rt△FGH(HL),∴EH=GH,
∵矩形EBFG∽矩形ABCD,∴==n,∴=n,
∴=,
由(1)知:△ABE∽△DEH,∴==,∴=,∴nx=2a,
∴=,∴tan∠ABE===;
②如图3,BF=FH,
∵矩形EBFG∽矩形ABCD,
∴∠ABC=∠EBF=90°,=,
∴∠ABE=∠CBF,∴△ABE∽△CBF,
∴∠BCF=∠A=90°,∴D,C,F共线,
∵BF=FH,∴∠FBH=∠FHB,∵EG∥BF,
∴∠FBH=∠EHB,∴∠EHB=∠CHB,
∵BE⊥EH,BC⊥CH,∴BE=BC,
由①可知:AB=x,AE=a,BE=BC=nx,
由勾股定理得:AB2+AE2=BE2,
∴x2+a2=(nx)2,∴x=(负值舍),
∴tan∠ABE===,
综上,tan∠ABE的值是或.
PAGE
同课章节目录
