2025年九年级中考数学基础知识专项训练题15 图形相似(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题15 图形相似(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 729.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 18:40:52 | ||
图片预览



文档简介
2025中考数学基础知识专项训练题15 图形相似
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题:(每小题3分, 共30分)
1.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上,若线段,则线段BC的长是( )
A.2 B.4 C.1 D.3
2.已知.则它们的周长比为( )
A. B. C. D.
3.在某一时刻,测得一根高为的竹竿的影长为,同时测得一栋楼的影长为,则这栋楼的高度是( )
A. B. C. D.
4.数学实践活动课上,小明和小强分别剪了一对三角形,他们经过测量得到相关数据,并标记在图形上.如图,对于他们剪的两组三角形的说法,正确的是( )
A.都相似 B.只有图①相似 C.只有图②相似 D.都不相似
5.如图,已知两个直角三角形关于原点O位似,且点A(3,—6)与点B(—1,b)是对应顶点,则b的值为( )
A.2 B.—2 C.18 D.—18
小颖同学是校园艺术节的主持人,学完黄金分割后她想,主持节目时如果站在舞台长的黄金分割点的位置,会让台下的同学们看起来效果更好,于是她将舞台的长看作线段AB,量得AB=8米,若点C是线段AB的黄金分割点(AC>BC),则线段AC的长为( )
A. B. C. D.
7.如图,在△ABC中,D在AC上,DE∥BC,DF∥AB,若,则的值为( )
A.1 B. C. D.
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为( )
A. B. C. D.
9.已知,则直线一定经过( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
10.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=,AD=2,将△ABC绕点C顺时针方向旋转后得△A’B’C’,当A’B’恰好过点D时,△B’CD为等腰三角形,若B’B=2,则AA’=( )
B. C. D.
二、填空题(11-14每题4分,15、16每小题5分,共26分)
11.设点是线段的黄金分割点,那么线段的长是___________.
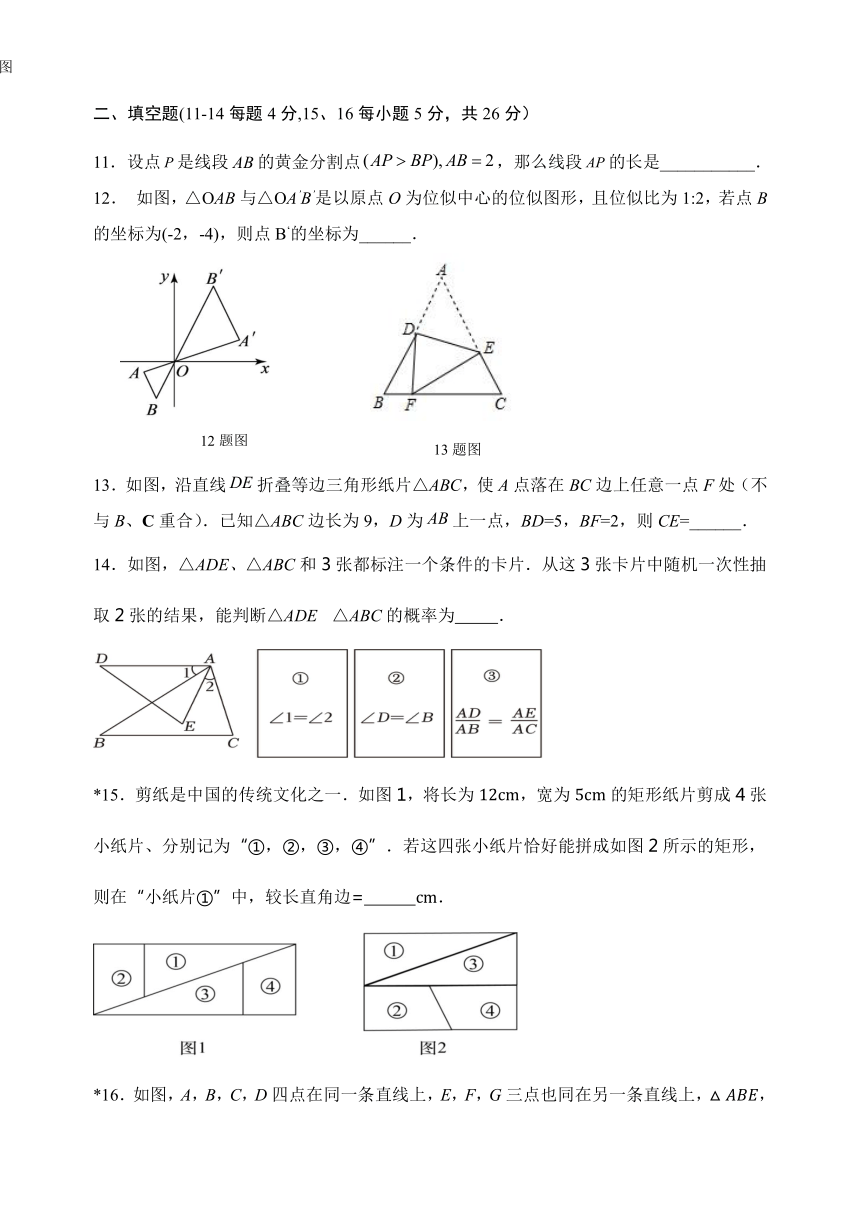
如图,△OAB与△OA’B’是以原点O为位似中心的位似图形,且位似比为1:2,若点B的坐标为(-2,-4),则点B‘的坐标为______.
13.如图,沿直线折叠等边三角形纸片△ABC,使A点落在BC边上任意一点F处(不与B、C重合).已知△ABC边长为9,D为上一点,BD=5,BF=2,则CE=______.
14.如图,△ADE、△ABC和3张都标注一个条件的卡片.从这3张卡片中随机一次性抽取2张的结果,能判断△ADE△ABC的概率为 .
*15.剪纸是中国的传统文化之一.如图1,将长为,宽为的矩形纸片剪成4张小纸片、分别记为“①,②,③,④”.若这四张小纸片恰好能拼成如图2所示的矩形,则在“小纸片①”中,较长直角边= .
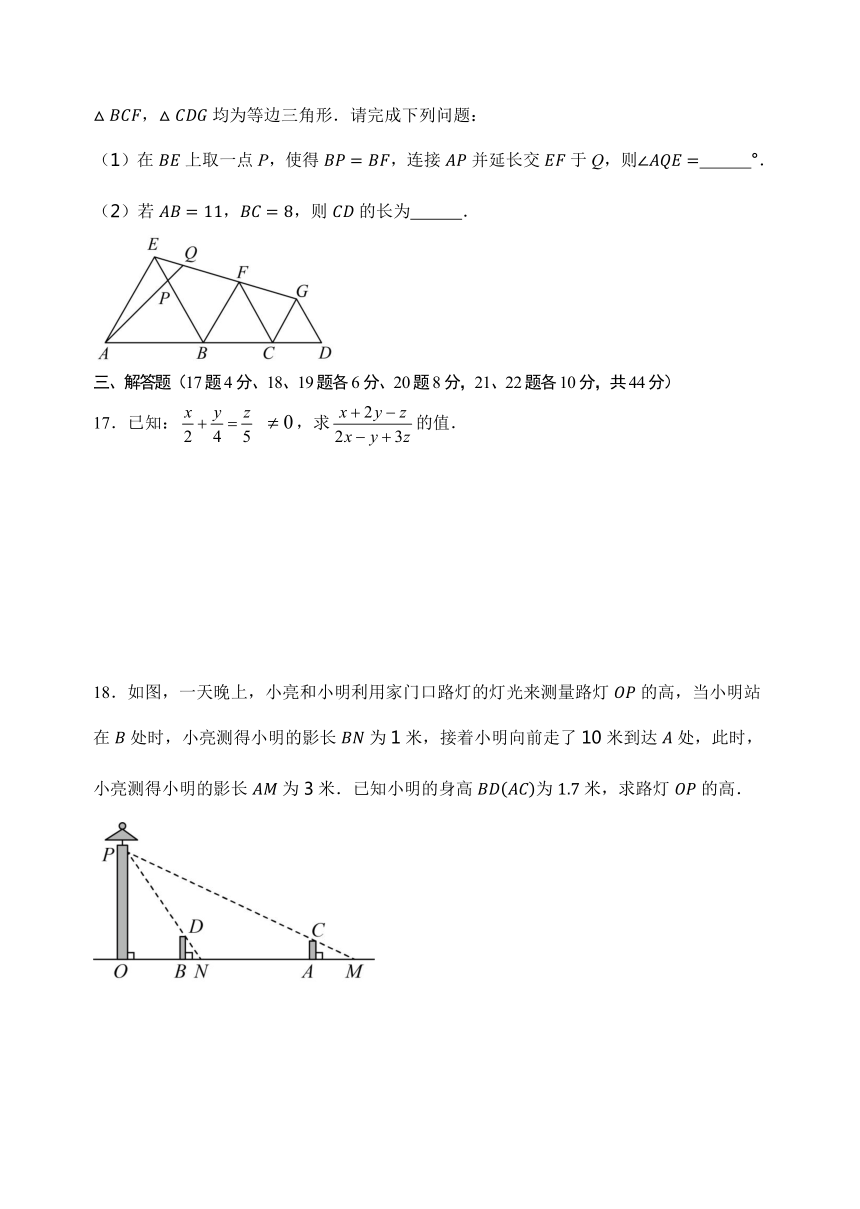
*16.如图,A,B,C,D四点在同一条直线上,E,F,G三点也同在另一条直线上,,,均为等边三角形.请完成下列问题:
(1)在上取一点P,使得,连接并延长交于Q,则 °.
(2)若,,则的长为 .
三、解答题(17题4分、18、19题各6分、20题8分,21、22题各10分,共44分)
17.已知: ,求的值.
18.如图,一天晚上,小亮和小明利用家门口路灯的灯光来测量路灯的高,当小明站在处时,小亮测得小明的影长为1米,接着小明向前走了10米到达处,此时,小亮测得小明的影长为3米.已知小明的身高为米,求路灯的高.
19.如图,在矩形ABCD中,AB=15cm ,BC=10cm ,点P沿AB边从点A开始向B点以2cm/s 的速度移动,点Q沿DA边从点D开始向点A以1cm/s 的速度移动.若P、 Q同时出发,用t(秒)表示移动时间.
(1)当t为何值时,△PAQ为等腰直角三角形?
(2)当t为何值时,以点P、A、Q为顶点的 △PAQ与△ABC 相似?
20.如图,在矩形中,点M是上一点,DN垂直平分,交AC于点E,交于点N,连接并延长交DC于点G,若.
(1)求证:点N是的中点;
(2)设,试用含a的代数式表示的长.
21.【教材呈现】华师版九年级上册63页例1.
如图,在中,点是边的三等分点,,,求的长.
【应用拓展】
(1)如图①,在中,点是边的中点,点为延长线上一点,连接交于点,若,,,则的长为 .
(2)如图②,在中,点为边延长线上一点,点为上一点,连接交于点,若点为的中点,,的面积为4,则(阴影部分)面积为 .
*22.综合实践课上,数学老师带领学生探究矩形的旋转.
【动手操作】
如图1,四边形是一张矩形纸片,,.先将矩形对折,使与重合,折痕为,沿剪开得到两个矩形.矩形保持不动,将矩形绕点逆时针旋转,点的对应点为,所在直线与所在直线交于点.
【探究发现】
(1)连接,,,根据______(填选项),证得,;
A.;B.;C.;D.
(2)数学老师让学生动手操作后提出问题:
①“勤奋”组发现,如图2,当点落在边上时,边恰好经过点,提出问题:求两个矩形重叠部分四边形的面积;请你直接写出四边形的面积_______;
②“好学”组提出问题:如图3,当落在上时,连接,,发现,请你尝试证明;
【引申探究】
当点落在矩形中的平分线所在直线上时,请直接写出线段的长.
参考答案
一、选择题
1. D 2.A 3. C 4.A 5. A 6.B 7.D 8.C 9.B 10.A
二.填空题
11. 12. (4,8) 13. 14. . 15.
16.(1)60,(2)
三、解答题
17. 解:设,则x=2k,y=4k,z=5k, …………2分
∴ …………4分
18. 解:设,则,
由题意得,,
∴,
∴,
∵,
∴,即,
解得,
经检验,是原方程的解,
∴,
∵,
∴,
∴,
∴路灯的高为.
19.解:∵AB=15cm,BC=10cm,点P沿AB边从点A开始向B点以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动,
∴AQ=10﹣t,AP=2t,
∵△PAQ是等腰直角三角形,
∴10﹣t=2t,解得t=s …………2分
(2)∵以点Q、A、P为顶点的三角形与△ABC相似,
∴△ABC∽△PAQ或△ABC∽△QAP,
①当△ABC∽△PAQ时,
=,即=,
解得:t=;
②当△ABC∽△QAP时,
=,=,解得t=. …………6分
故当t=s或t=s时,以点Q、A、P为顶点的三角形与△ABC相似
20.(1)证明:∵垂直平分,
∴.
∵,
∴,
∴点N是的中点.
(2)解:∵四边形为矩形,
∴,
∴.
∵,,
∴,
∴,
∵,
∴,
∴.
∵,,
∴,
∴,
∴,
∴.
21.解:[教材呈现]
点是边的三等分点,
,
,
,
,
,
;
[应用拓展]
(1),
,
,
,
,即,
解得;
故答案为:16.
(2)过点作,
点为的中点,
,
,
,
的面积为4,
的面积为1,
的面积2,
,即,
的面积为.
故答案为:.
22.(1)证明:∵∠A=90° , ∠ABE=30°
∴ ∠AEB=60°
∵EB=ED ,
∴ ∠DBE= ∠EDB=30°
∵MN∥BD
∴∠DBE= ∠ENM,∠DBE= ∠EMN
∴∠ENM= ∠EMN
∴EN=EM
过点E作EH⊥MN 于点H,则MH=.
在Rt⊿EMH中,
∴
∴ …………3分
(2)在Rt⊿ABE中,∠ABE=30°,
∴DE=BE=2AE
∵AD=BC=6
∴AE=2,DE=BE=4
a.当点M在线段ED上时,过点N作NI⊥AD于点I,
在Rt⊿NIM中,
由(1)可知:,
∴
∴
b.当点M在线段ED延长线上时,过点N作⊥AD于点
在Rt⊿NI’M中, ,
在Rt⊿NI’E中,,
∴DM=NE -DE=,
∴
(3)连接CM,BD交于点N’.
∵M为DE的中点 ,
∴EM=MD=2,
∴.
∵ ,
∴,
∴,
∴∠DMC=60°,
∴.
∵MN∥BD
∴,
∴ ,
∵,
∴
又∵ ,
∴∽,
∴,即
∴
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题:(每小题3分, 共30分)
1.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上,若线段,则线段BC的长是( )
A.2 B.4 C.1 D.3
2.已知.则它们的周长比为( )
A. B. C. D.
3.在某一时刻,测得一根高为的竹竿的影长为,同时测得一栋楼的影长为,则这栋楼的高度是( )
A. B. C. D.
4.数学实践活动课上,小明和小强分别剪了一对三角形,他们经过测量得到相关数据,并标记在图形上.如图,对于他们剪的两组三角形的说法,正确的是( )
A.都相似 B.只有图①相似 C.只有图②相似 D.都不相似
5.如图,已知两个直角三角形关于原点O位似,且点A(3,—6)与点B(—1,b)是对应顶点,则b的值为( )
A.2 B.—2 C.18 D.—18
小颖同学是校园艺术节的主持人,学完黄金分割后她想,主持节目时如果站在舞台长的黄金分割点的位置,会让台下的同学们看起来效果更好,于是她将舞台的长看作线段AB,量得AB=8米,若点C是线段AB的黄金分割点(AC>BC),则线段AC的长为( )
A. B. C. D.
7.如图,在△ABC中,D在AC上,DE∥BC,DF∥AB,若,则的值为( )
A.1 B. C. D.
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为( )
A. B. C. D.
9.已知,则直线一定经过( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
10.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=,AD=2,将△ABC绕点C顺时针方向旋转后得△A’B’C’,当A’B’恰好过点D时,△B’CD为等腰三角形,若B’B=2,则AA’=( )
B. C. D.
二、填空题(11-14每题4分,15、16每小题5分,共26分)
11.设点是线段的黄金分割点,那么线段的长是___________.
如图,△OAB与△OA’B’是以原点O为位似中心的位似图形,且位似比为1:2,若点B的坐标为(-2,-4),则点B‘的坐标为______.
13.如图,沿直线折叠等边三角形纸片△ABC,使A点落在BC边上任意一点F处(不与B、C重合).已知△ABC边长为9,D为上一点,BD=5,BF=2,则CE=______.
14.如图,△ADE、△ABC和3张都标注一个条件的卡片.从这3张卡片中随机一次性抽取2张的结果,能判断△ADE△ABC的概率为 .
*15.剪纸是中国的传统文化之一.如图1,将长为,宽为的矩形纸片剪成4张小纸片、分别记为“①,②,③,④”.若这四张小纸片恰好能拼成如图2所示的矩形,则在“小纸片①”中,较长直角边= .
*16.如图,A,B,C,D四点在同一条直线上,E,F,G三点也同在另一条直线上,,,均为等边三角形.请完成下列问题:
(1)在上取一点P,使得,连接并延长交于Q,则 °.
(2)若,,则的长为 .
三、解答题(17题4分、18、19题各6分、20题8分,21、22题各10分,共44分)
17.已知: ,求的值.
18.如图,一天晚上,小亮和小明利用家门口路灯的灯光来测量路灯的高,当小明站在处时,小亮测得小明的影长为1米,接着小明向前走了10米到达处,此时,小亮测得小明的影长为3米.已知小明的身高为米,求路灯的高.
19.如图,在矩形ABCD中,AB=15cm ,BC=10cm ,点P沿AB边从点A开始向B点以2cm/s 的速度移动,点Q沿DA边从点D开始向点A以1cm/s 的速度移动.若P、 Q同时出发,用t(秒)表示移动时间.
(1)当t为何值时,△PAQ为等腰直角三角形?
(2)当t为何值时,以点P、A、Q为顶点的 △PAQ与△ABC 相似?
20.如图,在矩形中,点M是上一点,DN垂直平分,交AC于点E,交于点N,连接并延长交DC于点G,若.
(1)求证:点N是的中点;
(2)设,试用含a的代数式表示的长.
21.【教材呈现】华师版九年级上册63页例1.
如图,在中,点是边的三等分点,,,求的长.
【应用拓展】
(1)如图①,在中,点是边的中点,点为延长线上一点,连接交于点,若,,,则的长为 .
(2)如图②,在中,点为边延长线上一点,点为上一点,连接交于点,若点为的中点,,的面积为4,则(阴影部分)面积为 .
*22.综合实践课上,数学老师带领学生探究矩形的旋转.
【动手操作】
如图1,四边形是一张矩形纸片,,.先将矩形对折,使与重合,折痕为,沿剪开得到两个矩形.矩形保持不动,将矩形绕点逆时针旋转,点的对应点为,所在直线与所在直线交于点.
【探究发现】
(1)连接,,,根据______(填选项),证得,;
A.;B.;C.;D.
(2)数学老师让学生动手操作后提出问题:
①“勤奋”组发现,如图2,当点落在边上时,边恰好经过点,提出问题:求两个矩形重叠部分四边形的面积;请你直接写出四边形的面积_______;
②“好学”组提出问题:如图3,当落在上时,连接,,发现,请你尝试证明;
【引申探究】
当点落在矩形中的平分线所在直线上时,请直接写出线段的长.
参考答案
一、选择题
1. D 2.A 3. C 4.A 5. A 6.B 7.D 8.C 9.B 10.A
二.填空题
11. 12. (4,8) 13. 14. . 15.
16.(1)60,(2)
三、解答题
17. 解:设,则x=2k,y=4k,z=5k, …………2分
∴ …………4分
18. 解:设,则,
由题意得,,
∴,
∴,
∵,
∴,即,
解得,
经检验,是原方程的解,
∴,
∵,
∴,
∴,
∴路灯的高为.
19.解:∵AB=15cm,BC=10cm,点P沿AB边从点A开始向B点以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动,
∴AQ=10﹣t,AP=2t,
∵△PAQ是等腰直角三角形,
∴10﹣t=2t,解得t=s …………2分
(2)∵以点Q、A、P为顶点的三角形与△ABC相似,
∴△ABC∽△PAQ或△ABC∽△QAP,
①当△ABC∽△PAQ时,
=,即=,
解得:t=;
②当△ABC∽△QAP时,
=,=,解得t=. …………6分
故当t=s或t=s时,以点Q、A、P为顶点的三角形与△ABC相似
20.(1)证明:∵垂直平分,
∴.
∵,
∴,
∴点N是的中点.
(2)解:∵四边形为矩形,
∴,
∴.
∵,,
∴,
∴,
∵,
∴,
∴.
∵,,
∴,
∴,
∴,
∴.
21.解:[教材呈现]
点是边的三等分点,
,
,
,
,
,
;
[应用拓展]
(1),
,
,
,
,即,
解得;
故答案为:16.
(2)过点作,
点为的中点,
,
,
,
的面积为4,
的面积为1,
的面积2,
,即,
的面积为.
故答案为:.
22.(1)证明:∵∠A=90° , ∠ABE=30°
∴ ∠AEB=60°
∵EB=ED ,
∴ ∠DBE= ∠EDB=30°
∵MN∥BD
∴∠DBE= ∠ENM,∠DBE= ∠EMN
∴∠ENM= ∠EMN
∴EN=EM
过点E作EH⊥MN 于点H,则MH=.
在Rt⊿EMH中,
∴
∴ …………3分
(2)在Rt⊿ABE中,∠ABE=30°,
∴DE=BE=2AE
∵AD=BC=6
∴AE=2,DE=BE=4
a.当点M在线段ED上时,过点N作NI⊥AD于点I,
在Rt⊿NIM中,
由(1)可知:,
∴
∴
b.当点M在线段ED延长线上时,过点N作⊥AD于点
在Rt⊿NI’M中, ,
在Rt⊿NI’E中,,
∴DM=NE -DE=,
∴
(3)连接CM,BD交于点N’.
∵M为DE的中点 ,
∴EM=MD=2,
∴.
∵ ,
∴,
∴,
∴∠DMC=60°,
∴.
∵MN∥BD
∴,
∴ ,
∵,
∴
又∵ ,
∴∽,
∴,即
∴
同课章节目录
