2025年九年级中考数学基础知识专项训练题16 图形与坐标(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题16 图形与坐标(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览



文档简介
2025中考数学基础知识专项训练题16 图形与坐标
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题(每小题3分,共30分)
1.剪纸艺术是中国最古老的民间艺术之一,很多剪纸作品体现了数学中的对称美,如图所示的剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点的坐标为,则其关于轴对称的点的坐标为( )
A.(-3,-2) B.(3,-2) C.(-3,-2) D.(3,2)
2.在平面直角坐标系内有一点M在第三象限,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )
A.(-3,-4) B.(-4,-3) C.(-4,3) D.(-3,4)
3.若点A(-2,m)在正比例函数的图象上,则m的值是( )
A . B. C.1 D.-1
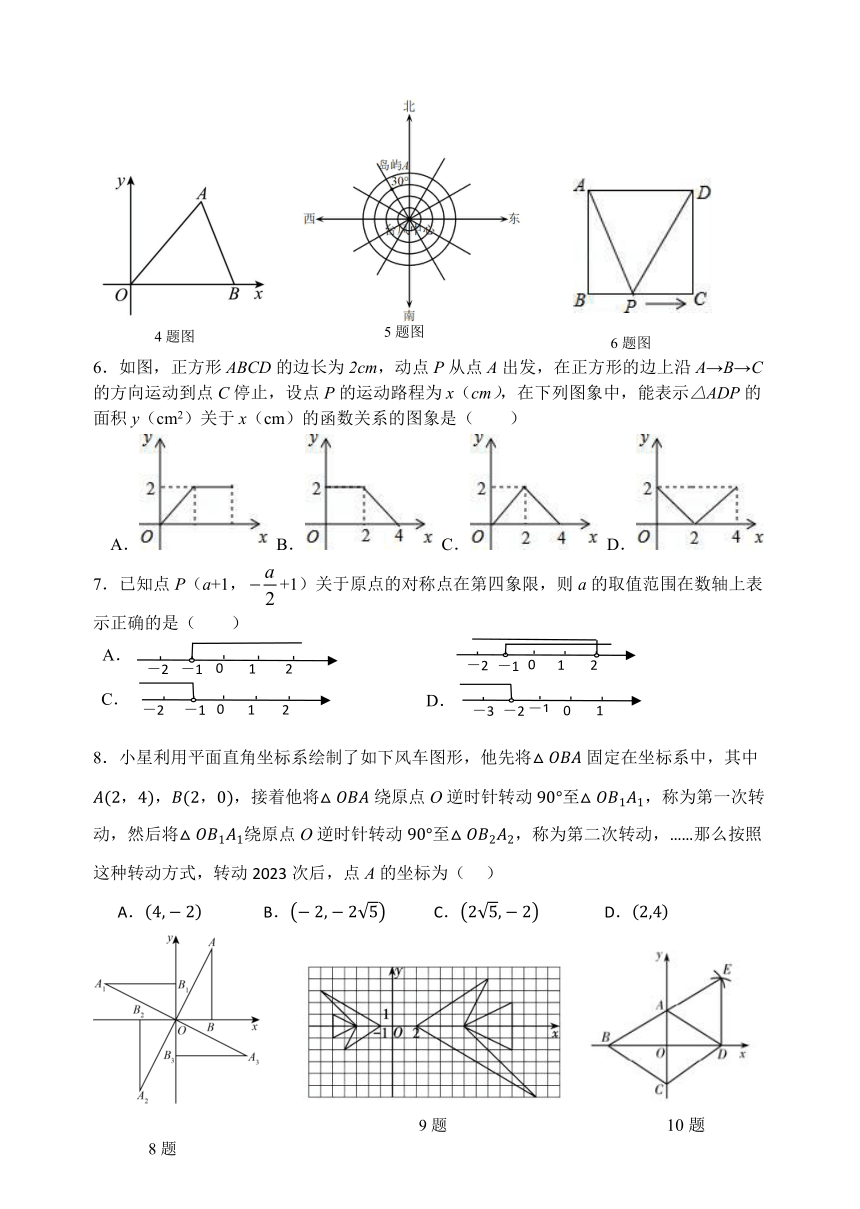
4.如图,风力发电机的三个相同叶片两两夹角为.以旋转轴为原点,水平方向为轴建立平面直角坐标系,恰好其中一个叶片尖点对应的坐标为.若叶片每秒绕点顺时针旋转,则第2023秒时叶片尖点的坐标为( )
A. B. C. D.
5..如图是某时刻卫星云图的示意图,每相邻两个圆之间的距离是10千米,以台风中心为观测点,岛屿A在( ).
A.北偏西方向30千米处 B.北偏东方向30千米处
C.西偏北方向20千米处 D.北偏西方向30千米处
6.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
7.已知点P(a+1,+1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
8.小星利用平面直角坐标系绘制了如下风车图形,他先将固定在坐标系中,其中,接着他将绕原点O逆时针转动至,称为第一次转动,然后将绕原点O逆时针转动至,称为第二次转动,……那么按照这种转动方式,转动2023次后,点A的坐标为( )
A. B. C. D.
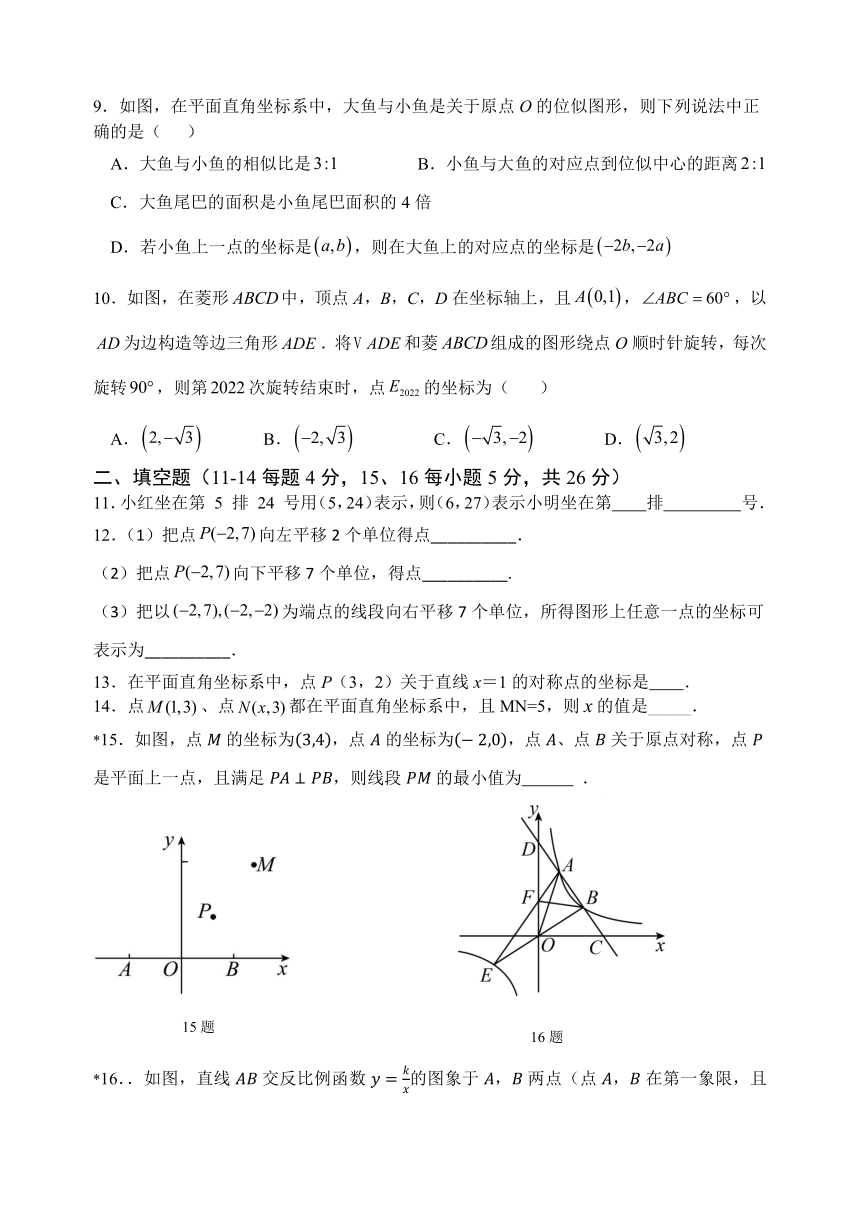
9.如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中正确的是( )
A.大鱼与小鱼的相似比是 B.小鱼与大鱼的对应点到位似中心的距离
C.大鱼尾巴的面积是小鱼尾巴面积的4倍
D.若小鱼上一点的坐标是,则在大鱼上的对应点的坐标是
10.如图,在菱形中,顶点A,B,C,D在坐标轴上,且,,以为边构造等边三角形.将和菱组成的图形绕点O顺时针旋转,每次旋转,则第次旋转结束时,点的坐标为( )
A. B. C. D.
二、填空题(11-14每题4分,15、16每小题5分,共26分)
11.小红坐在第 5 排 24 号用(5,24)表示,则(6,27)表示小明坐在第 排 号.
12.(1)把点向左平移2个单位得点__________.
(2)把点向下平移7个单位,得点__________.
(3)把以为端点的线段向右平移7个单位,所得图形上任意一点的坐标可表示为__________.
13.在平面直角坐标系中,点P(3,2)关于直线x=1的对称点的坐标是 .
14.点、点都在平面直角坐标系中,且MN=5,则的值是_____.
*15.如图,点的坐标为,点的坐标为,点、点关于原点对称,点是平面上一点,且满足,则线段的最小值为 .
*16..如图,直线交反比例函数的图象于两点(点在第一象限,且点在点的左侧),交轴于点,交轴于点,连接并延长交该反比例函数图象的另一支于点,连接交轴于点,连接,且.
(1)若,则 .
(2)若,则的值为 .
三、解答题(17题4分,18、19题各6分、20题8分、21、22题各10分,共44分)
17、如图,在中,,,分别以点,为圆心,大于的长为半径作弧,两弧交于点、,作直线交、于点、,连接,求的值.
18.若点P的坐标为(,2x-9),其中x满足不等式组,求点P所在的象限.
19.在平面直角坐标系中,一张矩形纸片按图所示放置.已知, ,将这张纸片折叠,使点落在边上,记作点,折痕与边(含端点)交于点,与边(含端点)或其延长线交于点.
()如图,若点的坐标为,求出点的坐标;
()若矩形沿直线折叠,求点的坐标;
20.疫情期间,市某医药公司销售N95口罩,经市场调查,该口罩每天的销售量 (盒)与销售单价(元)的函数关系如图1所示.设销售收入为元(销售收入=销售量×销售单价).
(1)若,求与的函数关系式;
(2)在(1)的条件下,求销售收入的最大值;
(3)市政府为了规范市场价格,均衡医疗资源,对口罩价格进行了调控,规定口罩的售价不得超过元,调控后销售收入与销售单价的函数关系如图2所示,若销售收入的最大值为元,求的值.
21.如图,在平面直角坐标系中,直线和直线交于点,四边形是矩形,点在轴正半轴上,点在轴正半轴上,点是矩形的边上的一个动点,连接,点关于直线的对称点为点.
(1)请直接写出点和点的坐标;
(2)当时,求点的坐标;
(3)若点到矩形的较长两条对边的距离之比为,请直接写出此时点的横坐标.
*22.如图,直线与坐标轴交于A,B两点,点C坐标为,将B点向右平移4个单位,再向下平移1个单位得到点D,直线交直线于点E.
(1)求直线的表达式;
(2)我们定义:如果一个三角形中有一个内角为,则称这个三角形为“天府三角形”
①点F是直线上第一象限内一点,若为“天府三角形”,求点F的坐标;
②在①的条件下,当点F的横坐标大于时,作点B关于x轴的对称点,点P为直线上的一个动点,连接,点Q为线段的中点,连接,当最小时,求点Q的坐标.
参考答案
一、选择题
1、D 2、 B 3、C 4、B 5、D 6、D 7、A 8、A 9、C 10、C
二、填空题
11、 6,27 12、 ; ; (其中m满足) 13、(﹣1,2). 14、6或-4 15、3 16、(1),(2)10
三、解答题
17、解:在中,,
由题得为的垂直平分线
18.解:,
解①得:x≥4,
解②得:x≤4,
则不等式组的解是:x=4,
∵=1,2x﹣9=﹣1,
∴点P的坐标为(1,﹣1),
∴点P在的第四象限.
19解:()∵点的坐标为,
∴,
∵四边形是矩形,
∴,
∴,
∴,
∴点的坐标为; ………2分
()如图,过点作于,
∵解析式为,
∴点的坐标为,
∴,
∴点的坐标为,
∴,
∵与全等,
∴, ,
∵点在上,且,
∴,
又∵,
∴,
∵,
∴ △DEA∽ △GAF
∴,
∵,
∴,
∴,
∴点的坐标为.………6分
20、解:(1)∵,
设解析式为,
把代入得:,
解得,
∴;
(2)
,
∵,开口向下,有最大值,
当时,最大值为,
答:收入的最大值为元;
(3)设解析式为,
把代入得:,
∴,
∴,
∴,
由图2得,函数在对称轴处取得最大值,最大值为,
∴,
解得,,
由(2)得,当,最大值为时,,不符合规定口罩的售价不得超过元,
当,最大值为时,,符合题意,
∴.
21.(1)解:联立,
解得:,故点,
故点、的坐标分别为、;
(2)解:当时,
,
解得:,
故点;
(3)解:点关于直线的对称点为点,连接,过点作轴于点,
①当点在直线下方时,
点到矩形的较长两条对边的距离之比为,则,
而,则,即点,
点关于直线的对称点为点,
为的中点,即
设直线的表达式为,
可得,解得,
则直线的表达式为:,
当时,,
故点;
②当点在直线上方时,
则,
同理可得:点;
③在下方时,
同理可得:,
综上,点或或.
22. (1)解:在中,当时,,
∴;
∵将点向右平移4个单位,再向下平移1个单位得到点D,
∴,
设直线的解析式为,
∴,
解得,
∴直线的解析式为;
(2)解:①如图2-1所示,当时,
在中,当时,,
∴,
∴,
∴,
∴,
∴,
∴点F的横坐标为4,
在中,当时,,
∴;
如图2-2所示,当时,过点作且,过点E作轴,根本过点H,D作的垂线,垂足分别为G、T,
联立,解得,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
同理可得直线的解析式为,
联立,解得,
∴;
综上所述,或;
②∵点是点B关于x轴的对称点,
∴,
∵点F的横坐标大于,
∴由(2)①得点F的坐标为,
∴直线即为直线,
∵点P在直线上运动,即点P的横坐标为4,
∵点Q为的中点,
∴点Q的横坐标为1,,
∴点Q在直线上运动,
如图所示,作点关于直线的对称点M,连接,
∴,
由轴对称的性质可得,
∵,
∴当三点共线时,最小,即此时最小,
同理求得直线的解析式为,
在中,当时,,
∴.
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题(每小题3分,共30分)
1.剪纸艺术是中国最古老的民间艺术之一,很多剪纸作品体现了数学中的对称美,如图所示的剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点的坐标为,则其关于轴对称的点的坐标为( )
A.(-3,-2) B.(3,-2) C.(-3,-2) D.(3,2)
2.在平面直角坐标系内有一点M在第三象限,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )
A.(-3,-4) B.(-4,-3) C.(-4,3) D.(-3,4)
3.若点A(-2,m)在正比例函数的图象上,则m的值是( )
A . B. C.1 D.-1
4.如图,风力发电机的三个相同叶片两两夹角为.以旋转轴为原点,水平方向为轴建立平面直角坐标系,恰好其中一个叶片尖点对应的坐标为.若叶片每秒绕点顺时针旋转,则第2023秒时叶片尖点的坐标为( )
A. B. C. D.
5..如图是某时刻卫星云图的示意图,每相邻两个圆之间的距离是10千米,以台风中心为观测点,岛屿A在( ).
A.北偏西方向30千米处 B.北偏东方向30千米处
C.西偏北方向20千米处 D.北偏西方向30千米处
6.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
7.已知点P(a+1,+1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
8.小星利用平面直角坐标系绘制了如下风车图形,他先将固定在坐标系中,其中,接着他将绕原点O逆时针转动至,称为第一次转动,然后将绕原点O逆时针转动至,称为第二次转动,……那么按照这种转动方式,转动2023次后,点A的坐标为( )
A. B. C. D.
9.如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中正确的是( )
A.大鱼与小鱼的相似比是 B.小鱼与大鱼的对应点到位似中心的距离
C.大鱼尾巴的面积是小鱼尾巴面积的4倍
D.若小鱼上一点的坐标是,则在大鱼上的对应点的坐标是
10.如图,在菱形中,顶点A,B,C,D在坐标轴上,且,,以为边构造等边三角形.将和菱组成的图形绕点O顺时针旋转,每次旋转,则第次旋转结束时,点的坐标为( )
A. B. C. D.
二、填空题(11-14每题4分,15、16每小题5分,共26分)
11.小红坐在第 5 排 24 号用(5,24)表示,则(6,27)表示小明坐在第 排 号.
12.(1)把点向左平移2个单位得点__________.
(2)把点向下平移7个单位,得点__________.
(3)把以为端点的线段向右平移7个单位,所得图形上任意一点的坐标可表示为__________.
13.在平面直角坐标系中,点P(3,2)关于直线x=1的对称点的坐标是 .
14.点、点都在平面直角坐标系中,且MN=5,则的值是_____.
*15.如图,点的坐标为,点的坐标为,点、点关于原点对称,点是平面上一点,且满足,则线段的最小值为 .
*16..如图,直线交反比例函数的图象于两点(点在第一象限,且点在点的左侧),交轴于点,交轴于点,连接并延长交该反比例函数图象的另一支于点,连接交轴于点,连接,且.
(1)若,则 .
(2)若,则的值为 .
三、解答题(17题4分,18、19题各6分、20题8分、21、22题各10分,共44分)
17、如图,在中,,,分别以点,为圆心,大于的长为半径作弧,两弧交于点、,作直线交、于点、,连接,求的值.
18.若点P的坐标为(,2x-9),其中x满足不等式组,求点P所在的象限.
19.在平面直角坐标系中,一张矩形纸片按图所示放置.已知, ,将这张纸片折叠,使点落在边上,记作点,折痕与边(含端点)交于点,与边(含端点)或其延长线交于点.
()如图,若点的坐标为,求出点的坐标;
()若矩形沿直线折叠,求点的坐标;
20.疫情期间,市某医药公司销售N95口罩,经市场调查,该口罩每天的销售量 (盒)与销售单价(元)的函数关系如图1所示.设销售收入为元(销售收入=销售量×销售单价).
(1)若,求与的函数关系式;
(2)在(1)的条件下,求销售收入的最大值;
(3)市政府为了规范市场价格,均衡医疗资源,对口罩价格进行了调控,规定口罩的售价不得超过元,调控后销售收入与销售单价的函数关系如图2所示,若销售收入的最大值为元,求的值.
21.如图,在平面直角坐标系中,直线和直线交于点,四边形是矩形,点在轴正半轴上,点在轴正半轴上,点是矩形的边上的一个动点,连接,点关于直线的对称点为点.
(1)请直接写出点和点的坐标;
(2)当时,求点的坐标;
(3)若点到矩形的较长两条对边的距离之比为,请直接写出此时点的横坐标.
*22.如图,直线与坐标轴交于A,B两点,点C坐标为,将B点向右平移4个单位,再向下平移1个单位得到点D,直线交直线于点E.
(1)求直线的表达式;
(2)我们定义:如果一个三角形中有一个内角为,则称这个三角形为“天府三角形”
①点F是直线上第一象限内一点,若为“天府三角形”,求点F的坐标;
②在①的条件下,当点F的横坐标大于时,作点B关于x轴的对称点,点P为直线上的一个动点,连接,点Q为线段的中点,连接,当最小时,求点Q的坐标.
参考答案
一、选择题
1、D 2、 B 3、C 4、B 5、D 6、D 7、A 8、A 9、C 10、C
二、填空题
11、 6,27 12、 ; ; (其中m满足) 13、(﹣1,2). 14、6或-4 15、3 16、(1),(2)10
三、解答题
17、解:在中,,
由题得为的垂直平分线
18.解:,
解①得:x≥4,
解②得:x≤4,
则不等式组的解是:x=4,
∵=1,2x﹣9=﹣1,
∴点P的坐标为(1,﹣1),
∴点P在的第四象限.
19解:()∵点的坐标为,
∴,
∵四边形是矩形,
∴,
∴,
∴,
∴点的坐标为; ………2分
()如图,过点作于,
∵解析式为,
∴点的坐标为,
∴,
∴点的坐标为,
∴,
∵与全等,
∴, ,
∵点在上,且,
∴,
又∵,
∴,
∵,
∴ △DEA∽ △GAF
∴,
∵,
∴,
∴,
∴点的坐标为.………6分
20、解:(1)∵,
设解析式为,
把代入得:,
解得,
∴;
(2)
,
∵,开口向下,有最大值,
当时,最大值为,
答:收入的最大值为元;
(3)设解析式为,
把代入得:,
∴,
∴,
∴,
由图2得,函数在对称轴处取得最大值,最大值为,
∴,
解得,,
由(2)得,当,最大值为时,,不符合规定口罩的售价不得超过元,
当,最大值为时,,符合题意,
∴.
21.(1)解:联立,
解得:,故点,
故点、的坐标分别为、;
(2)解:当时,
,
解得:,
故点;
(3)解:点关于直线的对称点为点,连接,过点作轴于点,
①当点在直线下方时,
点到矩形的较长两条对边的距离之比为,则,
而,则,即点,
点关于直线的对称点为点,
为的中点,即
设直线的表达式为,
可得,解得,
则直线的表达式为:,
当时,,
故点;
②当点在直线上方时,
则,
同理可得:点;
③在下方时,
同理可得:,
综上,点或或.
22. (1)解:在中,当时,,
∴;
∵将点向右平移4个单位,再向下平移1个单位得到点D,
∴,
设直线的解析式为,
∴,
解得,
∴直线的解析式为;
(2)解:①如图2-1所示,当时,
在中,当时,,
∴,
∴,
∴,
∴,
∴,
∴点F的横坐标为4,
在中,当时,,
∴;
如图2-2所示,当时,过点作且,过点E作轴,根本过点H,D作的垂线,垂足分别为G、T,
联立,解得,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
同理可得直线的解析式为,
联立,解得,
∴;
综上所述,或;
②∵点是点B关于x轴的对称点,
∴,
∵点F的横坐标大于,
∴由(2)①得点F的坐标为,
∴直线即为直线,
∵点P在直线上运动,即点P的横坐标为4,
∵点Q为的中点,
∴点Q的横坐标为1,,
∴点Q在直线上运动,
如图所示,作点关于直线的对称点M,连接,
∴,
由轴对称的性质可得,
∵,
∴当三点共线时,最小,即此时最小,
同理求得直线的解析式为,
在中,当时,,
∴.
同课章节目录
