2025年九年级中考数学基础知识专项训练题17 直角三角形的边角关系(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题17 直角三角形的边角关系(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 535.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 18:42:16 | ||
图片预览

文档简介
2025中考数学基础知识专项训练题17 直角三角形的边角关系
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题(每小题3分,共30分)
1.的相反数是( )
A.1 B. C. D.
2.在Rt△ABC中,∠C=90°,cosA=,则tanB的值为( )
A. B. C. D.
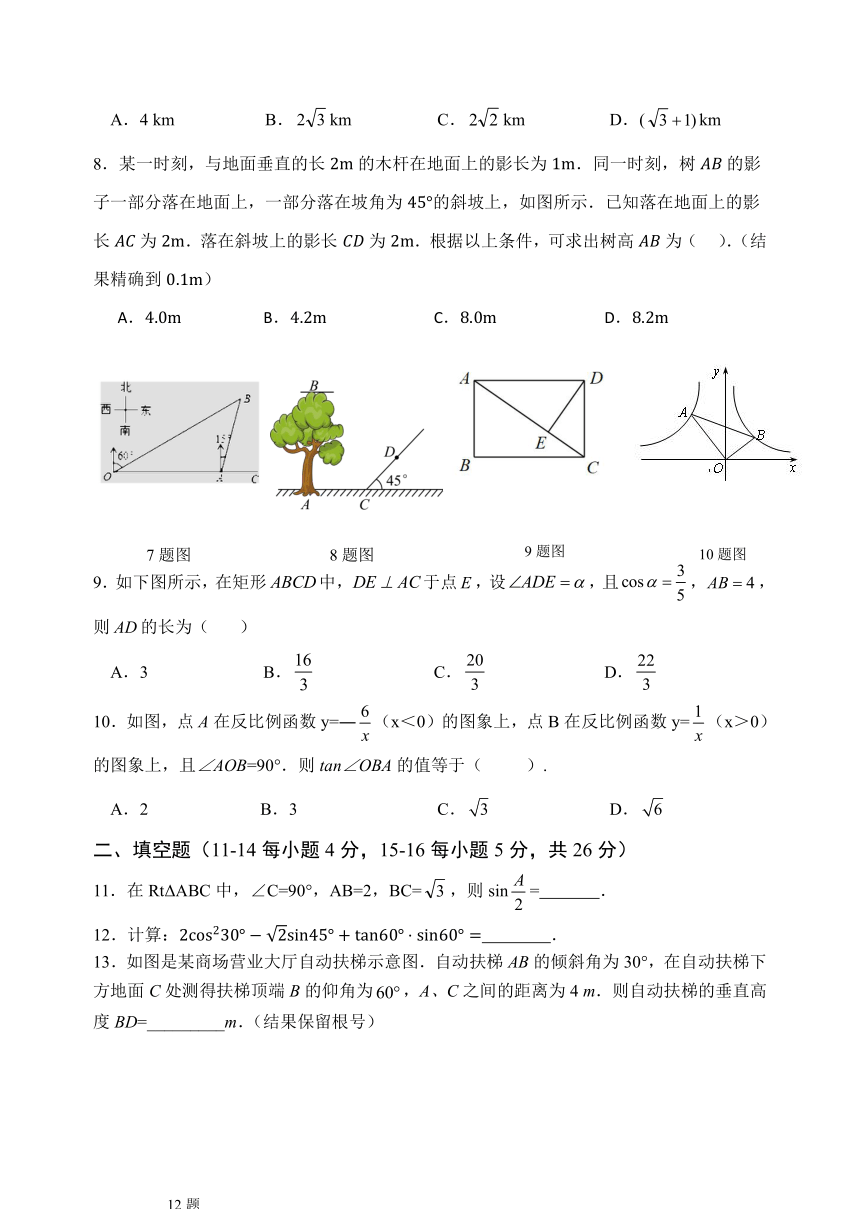
3.如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( ).
A. B. C. D.1
4.下列式子错误的是( )
A. B.
C. D.
5.如图是拦水坝的横断面,斜坡的水平宽度AC=18米,坡度为,则斜坡的垂直高度为( )
A.36米 B.12米 C.9米 D.6米
6.把一块直尺与一块三角板如图放置,若sin∠1=,则∠2的度数为( )
A.120° B.135° C.145° D.150°
7.如图,港口A在观测站O的正东方向,OA=4 km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( ).
A.4 km B.km C.km D.(km
8.某一时刻,与地面垂直的长的木杆在地面上的影长为.同一时刻,树的影子一部分落在地面上,一部分落在坡角为的斜坡上,如图所示.已知落在地面上的影长为.落在斜坡上的影长为.根据以上条件,可求出树高为( ).(结果精确到)
A. B. C. D.
9.如下图所示,在矩形中,于点,设,且,,则的长为( )
A.3 B. C. D.
10.如图,点A在反比例函数y=―(x<0)的图象上,点B在反比例函数y=(x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( ).
A.2 B.3 C. D.
二、填空题(11-14每小题4分,15-16每小题5分,共26分)
11.在RtΔABC中,∠C=90°,AB=2,BC=,则sin= .
12.计算: .
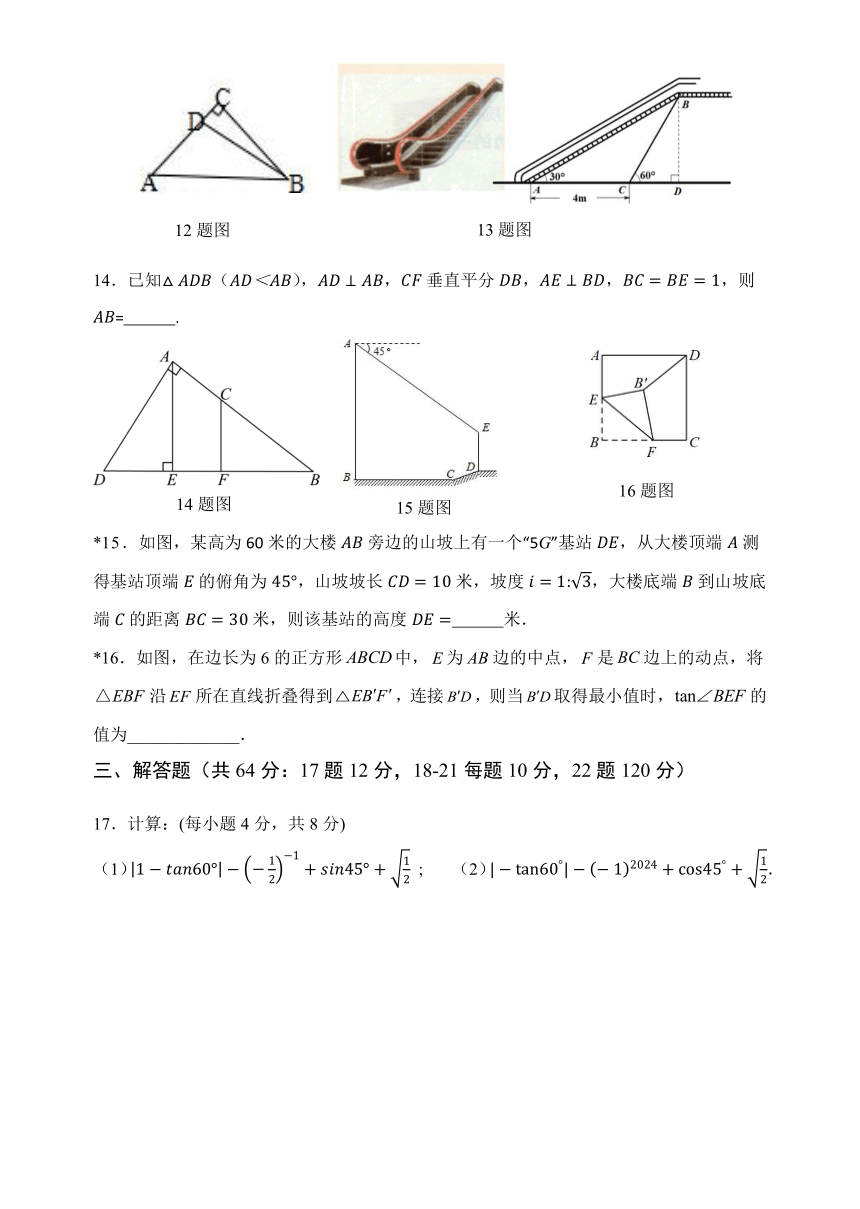
13.如图是某商场营业大厅自动扶梯示意图.自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为,A、C之间的距离为4 m.则自动扶梯的垂直高度BD=_________m.(结果保留根号)
14.已知,垂直平分,,,则= .
*15.如图,某高为60米的大楼旁边的山坡上有一个“5G”基站,从大楼顶端测得基站顶端的俯角为,山坡坡长米,坡度,大楼底端到山坡底端的距离米,则该基站的高度 米.
*16.如图,在边长为6的正方形中,为边的中点,是边上的动点,将沿所在直线折叠得到,连接,则当取得最小值时,的值为_____________.
三、解答题(共64分:17题12分,18-21每题10分,22题120分)
17.计算:(每小题4分,共8分)
(1) ; (2).
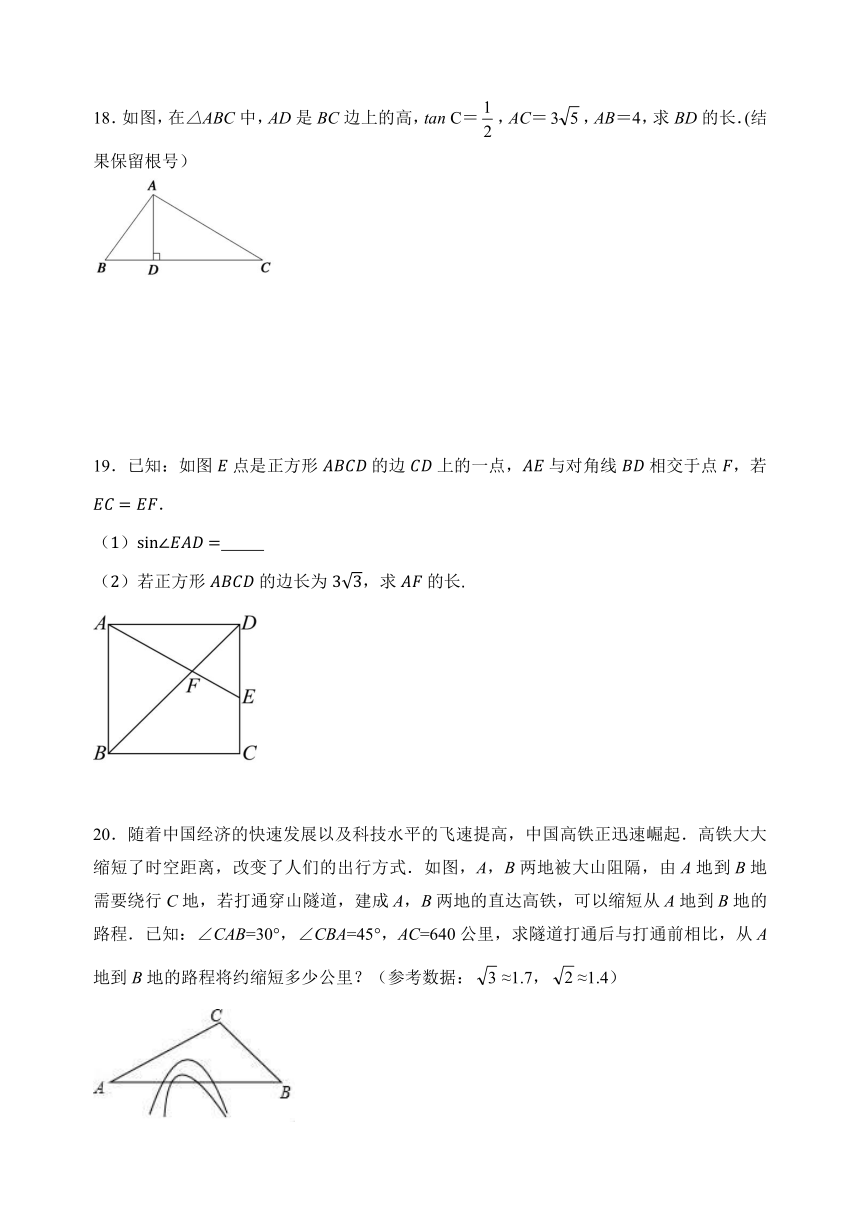
18.如图,在△ABC中,AD是BC边上的高,tan C=,AC=,AB=4,求BD的长.(结果保留根号)
19.已知:如图点是正方形的边上的一点,与对角线相交于点,若.
()
()若正方形的边长为,求的长.
20.随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4)
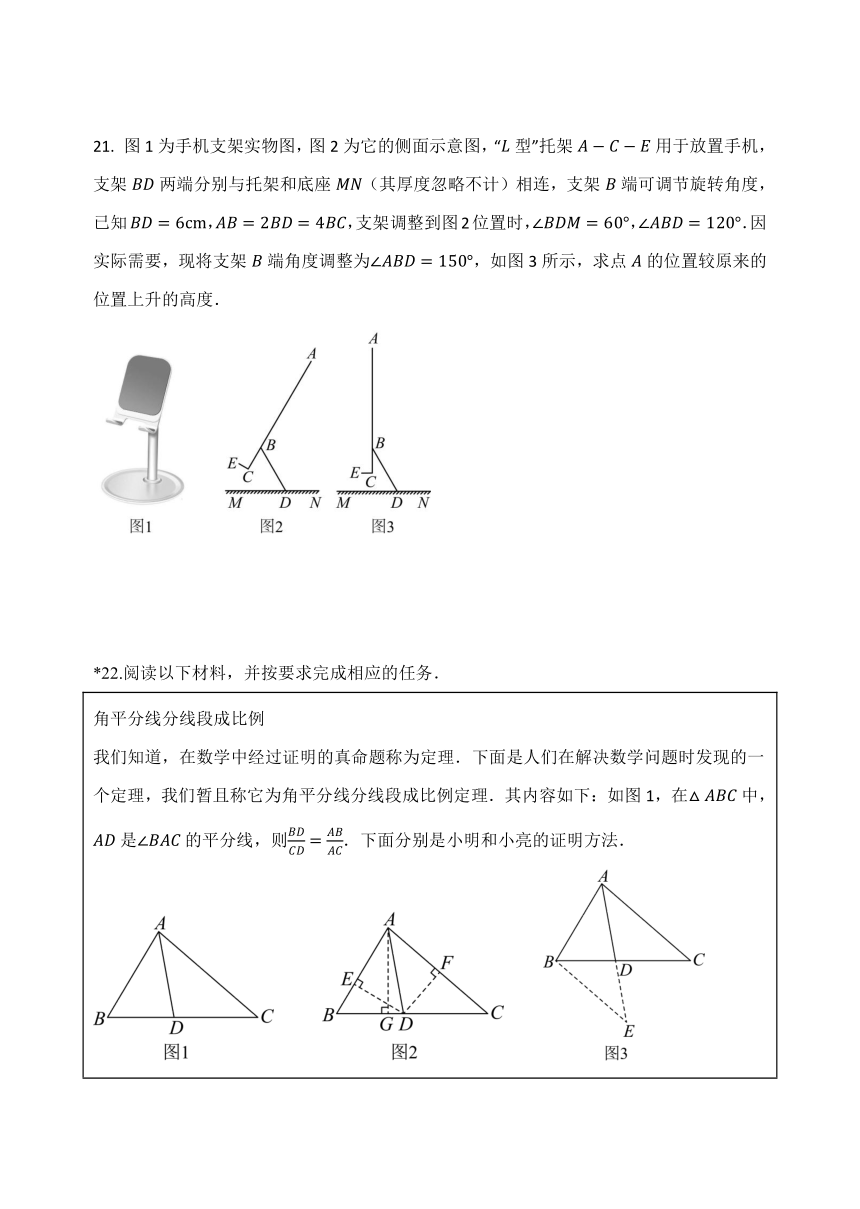
图1为手机支架实物图,图2为它的侧面示意图,“型”托架用于放置手机,支架两端分别与托架和底座(其厚度忽略不计)相连,支架端可调节旋转角度,已知,,支架调整到图2位置时,,.因实际需要,现将支架端角度调整为,如图3所示,求点的位置较原来的位置上升的高度.
*22.阅读以下材料,并按要求完成相应的任务.
角平分线分线段成比例 我们知道,在数学中经过证明的真命题称为定理.下面是人们在解决数学问题时发现的一个定理,我们暂且称它为角平分线分线段成比例定理.其内容如下:如图1,在中,是的平分线,则.下面分别是小明和小亮的证明方法. 小明:如图2,过点A作于点G,过点D分别作于点E,于点F. ∵AD是的平分线, ∵.(依据) ∵,, ∴. ∵,, ∴. ∴. 小亮:如图3,过点B作交的延长线于点E. ∵是的平分线, ∴. ∵, ∴.……
任务:
(1)小明的证明过程中的“依据”指的是______;
(2)小亮的证明过程不完善,请你帮助小亮完成证明;
(3)如图4,在中,,,.若的平分线交于点D,则的值为______.
参考答案
一、选择题
1.B 2.B 3. B 4.C 5.C 6. B 7.C 8.D 9.B 10.D
二、填空题
11. ; 12. 2 ; 13.;14 .; 15. ; 16.
三、解答题
17.(1)解:原式
;
(2)解:原式
18. 解:AD是BC边上的高.∴∠ADC=∠ADB=90°,
在Rt△ADC中,
∵tan C=,∴=.
∴CD=2AD,∴AD2+(2AD)2=(3)2,
∴AD=3,∴在Rt△ADB中,BD==.
19.解:();
()∵正方形的边长为,
∴,
∵,
∴,,
∴,,
∴,
∴,
故答案为:.
20、【解答】解:过点C作CD⊥AB于点D,
在Rt△ADC和Rt△BCD中,
∵∠CAB=30°,∠CBA=45°,AC=640,
∴CD=320,AD=320,
∴BD=CD=320,BC=320,
∴AC+BC=640+320≈1088,
∴AB=AD+BD=320+320≈864,
∴1088﹣864=224(公里),
答:隧道打通后与打通前相比,从A地到B地的路程将约缩短224公里.
21.解:如图2,过点作交于点,过点作交于点,过点作于点,如图3,延长交于点
旋转前如图3:
∵,,,
∴,
∵,,
∴,
∵,
∴在和中,
,
,
故点到的距离为: ,
旋转后如图3:
∵,
∴,
∵,
∴,
在中,
,
故 ,
点的位置较原来的位置上升高度为: ,
22.(1)解:依据为角平分线的性质定理,
故答案为:角平分线的性质定理;
(2)如图3,过点B作交的延长线于点E.
∵是的平分线,
∴.
∵,
∴.
∴.
∴.
∵,
∴.
∴.
∴.
(3)解:∵,,,
∴,
的平分线交于点D,
∴,且,
∴,
∴.
(本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.)
一、选择题(每小题3分,共30分)
1.的相反数是( )
A.1 B. C. D.
2.在Rt△ABC中,∠C=90°,cosA=,则tanB的值为( )
A. B. C. D.
3.如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( ).
A. B. C. D.1
4.下列式子错误的是( )
A. B.
C. D.
5.如图是拦水坝的横断面,斜坡的水平宽度AC=18米,坡度为,则斜坡的垂直高度为( )
A.36米 B.12米 C.9米 D.6米
6.把一块直尺与一块三角板如图放置,若sin∠1=,则∠2的度数为( )
A.120° B.135° C.145° D.150°
7.如图,港口A在观测站O的正东方向,OA=4 km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( ).
A.4 km B.km C.km D.(km
8.某一时刻,与地面垂直的长的木杆在地面上的影长为.同一时刻,树的影子一部分落在地面上,一部分落在坡角为的斜坡上,如图所示.已知落在地面上的影长为.落在斜坡上的影长为.根据以上条件,可求出树高为( ).(结果精确到)
A. B. C. D.
9.如下图所示,在矩形中,于点,设,且,,则的长为( )
A.3 B. C. D.
10.如图,点A在反比例函数y=―(x<0)的图象上,点B在反比例函数y=(x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( ).
A.2 B.3 C. D.
二、填空题(11-14每小题4分,15-16每小题5分,共26分)
11.在RtΔABC中,∠C=90°,AB=2,BC=,则sin= .
12.计算: .
13.如图是某商场营业大厅自动扶梯示意图.自动扶梯AB的倾斜角为30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角为,A、C之间的距离为4 m.则自动扶梯的垂直高度BD=_________m.(结果保留根号)
14.已知,垂直平分,,,则= .
*15.如图,某高为60米的大楼旁边的山坡上有一个“5G”基站,从大楼顶端测得基站顶端的俯角为,山坡坡长米,坡度,大楼底端到山坡底端的距离米,则该基站的高度 米.
*16.如图,在边长为6的正方形中,为边的中点,是边上的动点,将沿所在直线折叠得到,连接,则当取得最小值时,的值为_____________.
三、解答题(共64分:17题12分,18-21每题10分,22题120分)
17.计算:(每小题4分,共8分)
(1) ; (2).
18.如图,在△ABC中,AD是BC边上的高,tan C=,AC=,AB=4,求BD的长.(结果保留根号)
19.已知:如图点是正方形的边上的一点,与对角线相交于点,若.
()
()若正方形的边长为,求的长.
20.随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4)
图1为手机支架实物图,图2为它的侧面示意图,“型”托架用于放置手机,支架两端分别与托架和底座(其厚度忽略不计)相连,支架端可调节旋转角度,已知,,支架调整到图2位置时,,.因实际需要,现将支架端角度调整为,如图3所示,求点的位置较原来的位置上升的高度.
*22.阅读以下材料,并按要求完成相应的任务.
角平分线分线段成比例 我们知道,在数学中经过证明的真命题称为定理.下面是人们在解决数学问题时发现的一个定理,我们暂且称它为角平分线分线段成比例定理.其内容如下:如图1,在中,是的平分线,则.下面分别是小明和小亮的证明方法. 小明:如图2,过点A作于点G,过点D分别作于点E,于点F. ∵AD是的平分线, ∵.(依据) ∵,, ∴. ∵,, ∴. ∴. 小亮:如图3,过点B作交的延长线于点E. ∵是的平分线, ∴. ∵, ∴.……
任务:
(1)小明的证明过程中的“依据”指的是______;
(2)小亮的证明过程不完善,请你帮助小亮完成证明;
(3)如图4,在中,,,.若的平分线交于点D,则的值为______.
参考答案
一、选择题
1.B 2.B 3. B 4.C 5.C 6. B 7.C 8.D 9.B 10.D
二、填空题
11. ; 12. 2 ; 13.;14 .; 15. ; 16.
三、解答题
17.(1)解:原式
;
(2)解:原式
18. 解:AD是BC边上的高.∴∠ADC=∠ADB=90°,
在Rt△ADC中,
∵tan C=,∴=.
∴CD=2AD,∴AD2+(2AD)2=(3)2,
∴AD=3,∴在Rt△ADB中,BD==.
19.解:();
()∵正方形的边长为,
∴,
∵,
∴,,
∴,,
∴,
∴,
故答案为:.
20、【解答】解:过点C作CD⊥AB于点D,
在Rt△ADC和Rt△BCD中,
∵∠CAB=30°,∠CBA=45°,AC=640,
∴CD=320,AD=320,
∴BD=CD=320,BC=320,
∴AC+BC=640+320≈1088,
∴AB=AD+BD=320+320≈864,
∴1088﹣864=224(公里),
答:隧道打通后与打通前相比,从A地到B地的路程将约缩短224公里.
21.解:如图2,过点作交于点,过点作交于点,过点作于点,如图3,延长交于点
旋转前如图3:
∵,,,
∴,
∵,,
∴,
∵,
∴在和中,
,
,
故点到的距离为: ,
旋转后如图3:
∵,
∴,
∵,
∴,
在中,
,
故 ,
点的位置较原来的位置上升高度为: ,
22.(1)解:依据为角平分线的性质定理,
故答案为:角平分线的性质定理;
(2)如图3,过点B作交的延长线于点E.
∵是的平分线,
∴.
∵,
∴.
∴.
∴.
∵,
∴.
∴.
∴.
(3)解:∵,,,
∴,
的平分线交于点D,
∴,且,
∴,
∴.
同课章节目录
