【课堂无忧】苏教版六下2.3《圆柱的体积》(课件)
文档属性
| 名称 | 【课堂无忧】苏教版六下2.3《圆柱的体积》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览








文档简介
(共39张PPT)
2.3
圆柱的体积
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
探索并掌握圆柱的体积计算公式,并能应用公式解决相关的实际问题。
理解圆柱体积计算公式的推导过程,进一步体会转化的思想方法。
发展初步的推理能力和空间观念,渗透转化思想。
体积
体积的定义:
物体所占空间的大小叫体积
长方体和正方体体积的计算方法:
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体和正方体的体积=底面积×高
02
新知导入
体积
圆柱
的
圆柱所占空间的大小,叫作圆柱的体积。
02
新知导入
03
任务一
学习任务一
提出猜想
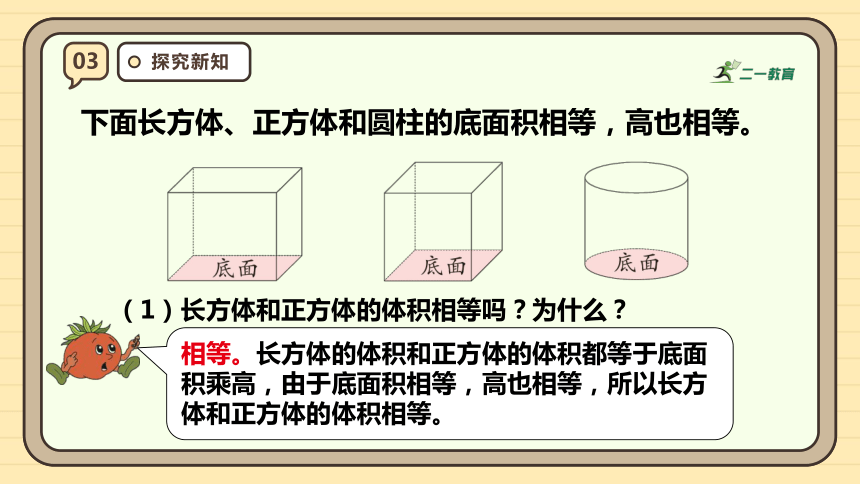
下面长方体、正方体和圆柱的底面积相等,高也相等。
(1)长方体和正方体的体积相等吗?为什么?
相等。长方体的体积和正方体的体积都等于底面积乘高,由于底面积相等,高也相等,所以长方体和正方体的体积相等。
03
探究新知
猜一猜,圆柱的体积与长方体、正方体的体积相等吗?用什么方法验证呢?
03
探究新知
圆柱的体积公式可能是
圆柱的体积=底面积×高
03
探究新知
04
任务二
学习任务二
验证猜想
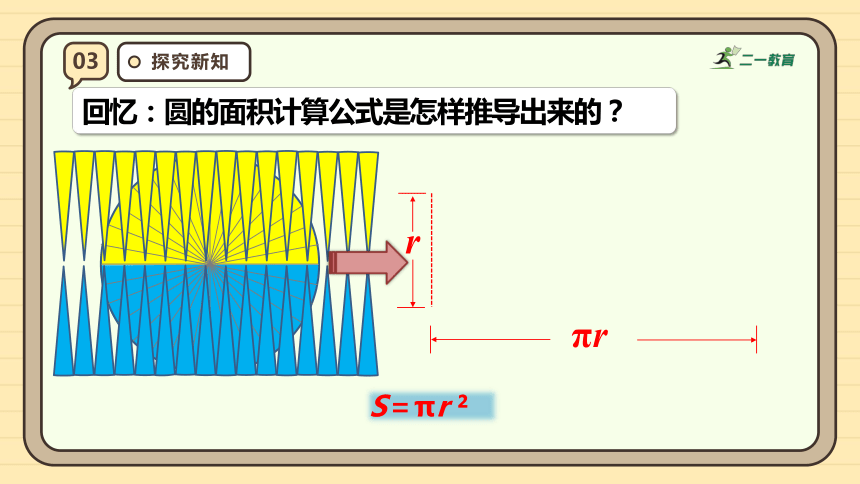
回忆:圆的面积计算公式是怎样推导出来的?
r
S=πr
πr
03
探究新知
把圆柱的底面平均分成16份
03
探究新知
切开
03
探究新知
拼接
拼成了一个近似的长方体。
03
探究新知
如果把圆柱的底面平均分成32份、64份……切开后拼成的物体会有什么变化?
平均分的份数越多,拼成的物体
就越接近长方体。
发现
03
探究新知
拼成的长方体与原来的圆柱有什么关系?
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
底面半径
长方体的宽
长方体的长
圆柱底面周长的一半
长方体的宽=圆柱的底面半径
长方体的长=圆柱底面周长的一半
03
探究新知
长方体的高等于圆柱的高。
长方体的高
圆柱的高
拼成的长方体与原来的圆柱有什么关系?
03
探究新知
S底
S底
高
高
长方体的体积= 底面积 × 高
底面积
高
根据上面的实验和讨论,想一想,可以怎样求圆柱的体积?
圆柱体的体积=
×
03
探究新知
04
任务二
学习任务二
得出结论
如果用V 表示圆柱的体积,S 表示圆柱的底面积,h表示圆柱的高,圆柱的体积公式可以写成:
V =Sh
= πr2h
04
探究新知
回顾圆柱体积公式的探索过程,你有什么体会?
04
探究新知
可以用长方体体积公式推导出圆柱体积公式。
04
探究新知
把圆柱转化成长方体,与探索圆面积的方法类似。
04
探究新知
计算长方体、正方体、圆柱的体积都可以用底面积乘高。
04
探究新知
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π(d÷2)2h
已知底面周长和高:V = π(C÷2π)2h
根据不同的条件可以推导出不同的公式。
05
拓展延伸
V=s h
12 × 6
π× 3 × 7
2
π ×(6÷2) ×8
2
6
分
米
12平方分米
7分米
.
3分米
6分米
8分米
V=兀(d÷2)×h
2
V= 兀r × h
2
1.看图说算式。
----基础题
06
课堂练习
⑴ 一个圆柱的底面积是 15 平方厘米,高是 6 厘米。它的体积是( )。
⑵ 一个圆柱的底面半径是 3 分米,高是 10 分米。它的体积是( )。
90 立方厘米
90π立方分米
⑶ 一个圆柱的高是 5 分米,底面直径是 2 分米。它的体积是( )。
15.7 立方分米
⑷ 一个圆柱的体积是 180 立方分米,底面积是 30 平方分米。它的高是( )。
6 分米
----基础题
06
课堂练习
3.一个圆柱形状的零件,底面半径是 5 厘米,高是 8厘米 。它的体积是多少立方厘米?
答: 它的体积是 628立方厘米。
200π(立方厘米)
π× 5 ×8 =
2
----基础题
06
课堂练习
4.挖一口圆柱形水井,地面以下的井深为10 m,底面直径为1 m。挖出的土有多少立方米?
答:挖出的土有7.85 m3。
3.14 ×(1÷2) ×10=7.85(m3)
已知底面直径和高:V = π ( d÷2 ) 2h
06
课堂练习----提高题
3.14×3 ×10=282.6(立方厘米)
答:东东和客人每人一杯不够。
282.6×4=1130.4(立方厘米)
1升=1000毫升=1000立方厘米
1130.4>1000
5.东东家来了三位小客人,妈妈冲了1升果汁。如果用底面半径是3厘米,高是10厘米的杯子喝果汁,东东和客人每人一杯够吗?
06
课堂练习----拓展题
我学会了计算圆柱的体积。
圆柱体积=圆柱的底面积×高
如果用V 表示圆柱的体积,S表示圆柱的底面积, h表示圆柱的高,圆柱的体积公式可以写成:
V = Sh
这节课你们都学会了哪些知识?
07
课堂小结
1.计算下面各圆柱的体积。
底面积/m2 高/m 体积/m3
0.6 1.2
0.25 3
0.72
0.75
08
作业布置
作业布置---知识技能类
(1)圆柱的高越高,体积越大。 ( )
(2)把一个圆柱体切拼成一个长方体,圆柱的表面积等于
长方体的表面积。 ( )
(3)体积相等的两个圆柱形状不一定相同。( )
×
×
√
2.火眼金睛。(对的打“√”,错的打“ ”)
08
作业布置
作业布置---知识技能类
3.育才小学建了两个同样大小的圆柱形花坛,花坛的底面直径为4米,高为0.8米。如果里面填土的高度为0.5米。两个花坛共填土多少立方米
π×( 4÷2 )2×0.5×2=4π(立方米)
答:两个花坛共填土4π立方米。
08
作业布置
作业布置---知识技能类
4.把一根长1 m的圆柱形木材锯成3段(每段仍是圆柱),表面积比原来增加了2.4 m2,这根木材原来的体积是多少
锯成3段增加了4个底面
2.4÷4×1=0.6(m3)
答:这根木材原来的体积是0.6 m3 。
08
作业布置---选做题
一张普通的长方形的白纸,用它可以卷成两个大小不同的圆柱。与同学交流,怎样卷成的圆柱体积比较大?
08
作业布置---综合实践类作业
09
板书设计
S底
S底
高
高
转化
长方体的体积= 底面积 × 高
底面积
高
圆柱体的体积=
×
用字母表示: V =Sh= πr2h
圆柱体的体积
https://www.21cnjy.com/recruitment/home/fine
2.3
圆柱的体积
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
探索并掌握圆柱的体积计算公式,并能应用公式解决相关的实际问题。
理解圆柱体积计算公式的推导过程,进一步体会转化的思想方法。
发展初步的推理能力和空间观念,渗透转化思想。
体积
体积的定义:
物体所占空间的大小叫体积
长方体和正方体体积的计算方法:
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体和正方体的体积=底面积×高
02
新知导入
体积
圆柱
的
圆柱所占空间的大小,叫作圆柱的体积。
02
新知导入
03
任务一
学习任务一
提出猜想
下面长方体、正方体和圆柱的底面积相等,高也相等。
(1)长方体和正方体的体积相等吗?为什么?
相等。长方体的体积和正方体的体积都等于底面积乘高,由于底面积相等,高也相等,所以长方体和正方体的体积相等。
03
探究新知
猜一猜,圆柱的体积与长方体、正方体的体积相等吗?用什么方法验证呢?
03
探究新知
圆柱的体积公式可能是
圆柱的体积=底面积×高
03
探究新知
04
任务二
学习任务二
验证猜想
回忆:圆的面积计算公式是怎样推导出来的?
r
S=πr
πr
03
探究新知
把圆柱的底面平均分成16份
03
探究新知
切开
03
探究新知
拼接
拼成了一个近似的长方体。
03
探究新知
如果把圆柱的底面平均分成32份、64份……切开后拼成的物体会有什么变化?
平均分的份数越多,拼成的物体
就越接近长方体。
发现
03
探究新知
拼成的长方体与原来的圆柱有什么关系?
长方体的体积与圆柱的体积相等。
长方体的底面积等于圆柱的底面积。
底面半径
长方体的宽
长方体的长
圆柱底面周长的一半
长方体的宽=圆柱的底面半径
长方体的长=圆柱底面周长的一半
03
探究新知
长方体的高等于圆柱的高。
长方体的高
圆柱的高
拼成的长方体与原来的圆柱有什么关系?
03
探究新知
S底
S底
高
高
长方体的体积= 底面积 × 高
底面积
高
根据上面的实验和讨论,想一想,可以怎样求圆柱的体积?
圆柱体的体积=
×
03
探究新知
04
任务二
学习任务二
得出结论
如果用V 表示圆柱的体积,S 表示圆柱的底面积,h表示圆柱的高,圆柱的体积公式可以写成:
V =Sh
= πr2h
04
探究新知
回顾圆柱体积公式的探索过程,你有什么体会?
04
探究新知
可以用长方体体积公式推导出圆柱体积公式。
04
探究新知
把圆柱转化成长方体,与探索圆面积的方法类似。
04
探究新知
计算长方体、正方体、圆柱的体积都可以用底面积乘高。
04
探究新知
已知底面积和高:V = Sh
已知底面半径和高:V = πr2h
已知底面直径和高:V = π(d÷2)2h
已知底面周长和高:V = π(C÷2π)2h
根据不同的条件可以推导出不同的公式。
05
拓展延伸
V=s h
12 × 6
π× 3 × 7
2
π ×(6÷2) ×8
2
6
分
米
12平方分米
7分米
.
3分米
6分米
8分米
V=兀(d÷2)×h
2
V= 兀r × h
2
1.看图说算式。
----基础题
06
课堂练习
⑴ 一个圆柱的底面积是 15 平方厘米,高是 6 厘米。它的体积是( )。
⑵ 一个圆柱的底面半径是 3 分米,高是 10 分米。它的体积是( )。
90 立方厘米
90π立方分米
⑶ 一个圆柱的高是 5 分米,底面直径是 2 分米。它的体积是( )。
15.7 立方分米
⑷ 一个圆柱的体积是 180 立方分米,底面积是 30 平方分米。它的高是( )。
6 分米
----基础题
06
课堂练习
3.一个圆柱形状的零件,底面半径是 5 厘米,高是 8厘米 。它的体积是多少立方厘米?
答: 它的体积是 628立方厘米。
200π(立方厘米)
π× 5 ×8 =
2
----基础题
06
课堂练习
4.挖一口圆柱形水井,地面以下的井深为10 m,底面直径为1 m。挖出的土有多少立方米?
答:挖出的土有7.85 m3。
3.14 ×(1÷2) ×10=7.85(m3)
已知底面直径和高:V = π ( d÷2 ) 2h
06
课堂练习----提高题
3.14×3 ×10=282.6(立方厘米)
答:东东和客人每人一杯不够。
282.6×4=1130.4(立方厘米)
1升=1000毫升=1000立方厘米
1130.4>1000
5.东东家来了三位小客人,妈妈冲了1升果汁。如果用底面半径是3厘米,高是10厘米的杯子喝果汁,东东和客人每人一杯够吗?
06
课堂练习----拓展题
我学会了计算圆柱的体积。
圆柱体积=圆柱的底面积×高
如果用V 表示圆柱的体积,S表示圆柱的底面积, h表示圆柱的高,圆柱的体积公式可以写成:
V = Sh
这节课你们都学会了哪些知识?
07
课堂小结
1.计算下面各圆柱的体积。
底面积/m2 高/m 体积/m3
0.6 1.2
0.25 3
0.72
0.75
08
作业布置
作业布置---知识技能类
(1)圆柱的高越高,体积越大。 ( )
(2)把一个圆柱体切拼成一个长方体,圆柱的表面积等于
长方体的表面积。 ( )
(3)体积相等的两个圆柱形状不一定相同。( )
×
×
√
2.火眼金睛。(对的打“√”,错的打“ ”)
08
作业布置
作业布置---知识技能类
3.育才小学建了两个同样大小的圆柱形花坛,花坛的底面直径为4米,高为0.8米。如果里面填土的高度为0.5米。两个花坛共填土多少立方米
π×( 4÷2 )2×0.5×2=4π(立方米)
答:两个花坛共填土4π立方米。
08
作业布置
作业布置---知识技能类
4.把一根长1 m的圆柱形木材锯成3段(每段仍是圆柱),表面积比原来增加了2.4 m2,这根木材原来的体积是多少
锯成3段增加了4个底面
2.4÷4×1=0.6(m3)
答:这根木材原来的体积是0.6 m3 。
08
作业布置---选做题
一张普通的长方形的白纸,用它可以卷成两个大小不同的圆柱。与同学交流,怎样卷成的圆柱体积比较大?
08
作业布置---综合实践类作业
09
板书设计
S底
S底
高
高
转化
长方体的体积= 底面积 × 高
底面积
高
圆柱体的体积=
×
用字母表示: V =Sh= πr2h
圆柱体的体积
https://www.21cnjy.com/recruitment/home/fine
