2025年九年级中考数学基础知识专项训练题10 四边形(含答案)
文档属性
| 名称 | 2025年九年级中考数学基础知识专项训练题10 四边形(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 00:00:00 | ||
图片预览

文档简介
金堂县2023—2024学年度下期单元质量检测题
九年级数学 (十)四边形
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
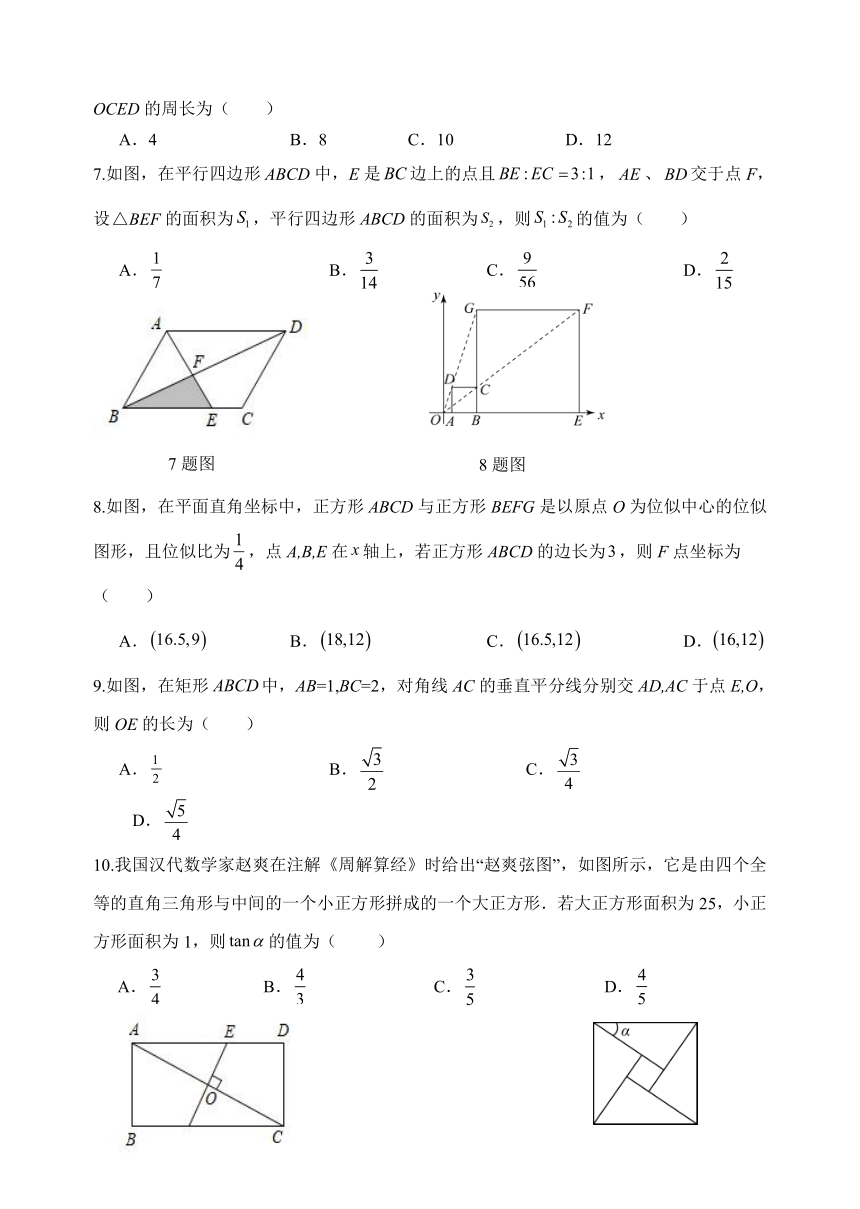
1.如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )
A.6 B.11 C.12 D.18
2.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
3.菱形的两条对角线的长分别是2cm和6cm,则菱形的面积是( )
A. B. C. D.
4.如图,将一张长方形纸片按如图方式折叠,BD,BE为折痕,若∠ABE=30°,则∠DBC的度数为( ).
A. B. C. D.
5.如图,矩形ABCD的对角线AC,BD相交于点O,点E是CD的中点,若OE=3,则BC的长为( )
A.3 B.4 C.5 D.6
6.矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
A.4 B.8 C.10 D.12
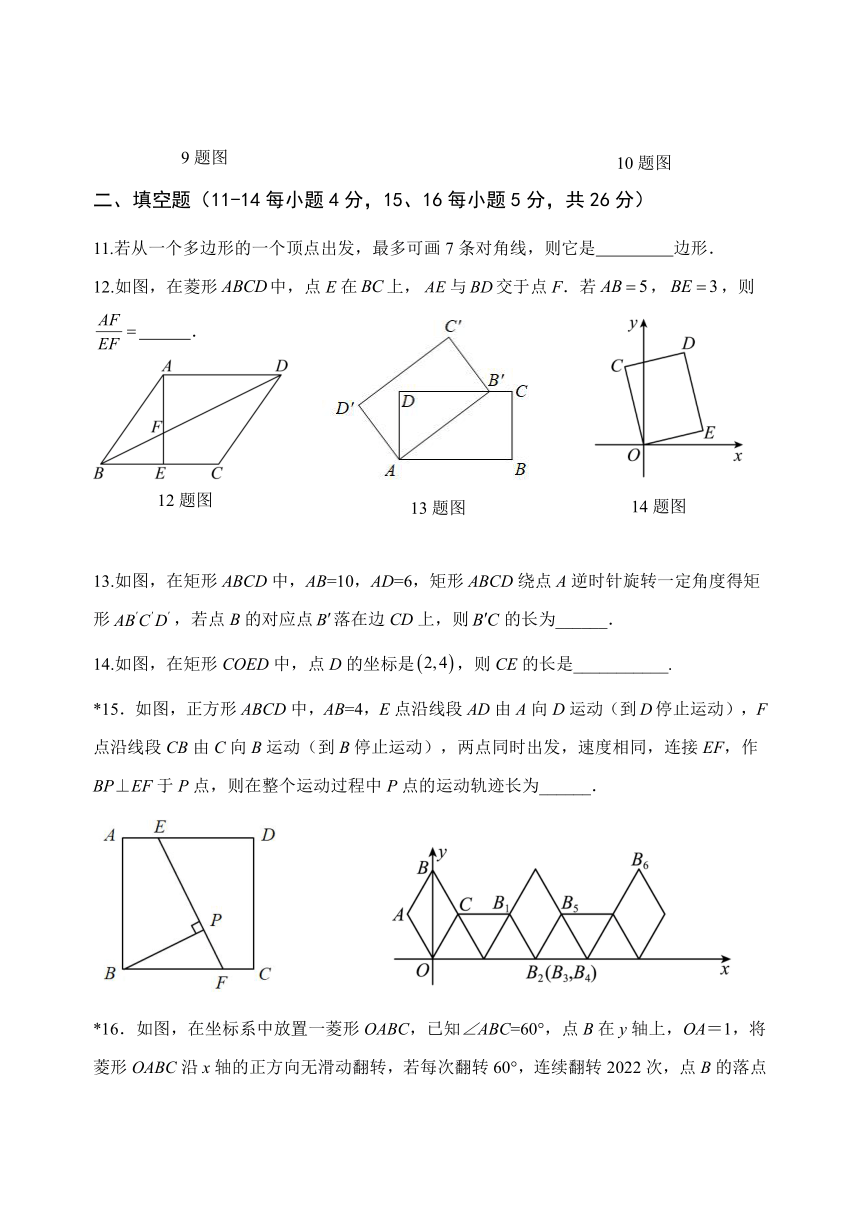
7.如图,在平行四边形ABCD中,E是边上的点且,、交于点F,设的面积为,平行四边形ABCD的面积为,则的值为( )
A. B. C. D.
8.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,点A,B,E在轴上,若正方形ABCD的边长为,则F点坐标为( )
A. B. C. D.
9.如图,在矩形中,AB=1,BC=2,对角线AC的垂直平分线分别交AD,AC于点E,O,则OE的长为( )
A. B. C. D.
10.我国汉代数学家赵爽在注解《周解算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形面积为25,小正方形面积为1,则的值为( )
A. B. C. D.
二、填空题(11-14每小题4分,15、16每小题5分,共26分)
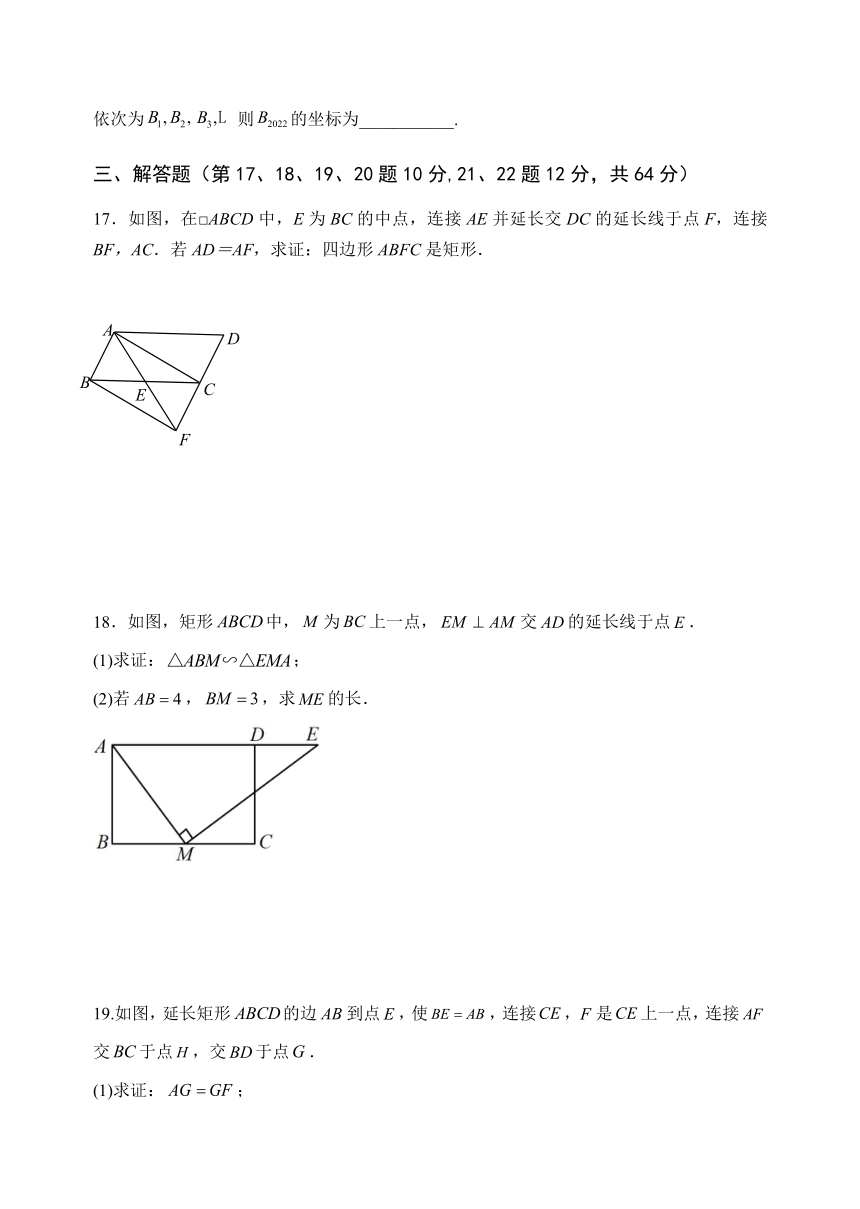
11.若从一个多边形的一个顶点出发,最多可画7条对角线,则它是 边形.
12.如图,在菱形中,点E在上,与交于点F.若,,则 .
13.如图,在矩形ABCD中,AB=10,AD=6,矩形ABCD绕点A逆时针旋转一定角度得矩形,若点B的对应点落在边CD上,则的长为______.
14.如图,在矩形COED中,点D的坐标是,则CE的长是___________.
*15.如图,正方形ABCD中,AB=4,E点沿线段AD由A向D运动(到停止运动),F点沿线段CB由C向B运动(到B停止运动),两点同时出发,速度相同,连接EF,作BP⊥EF于P点,则在整个运动过程中P点的运动轨迹长为______.
*16.如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,若每次翻转60°,连续翻转2022次,点B的落点依次为则的坐标为___________.
三、解答题(第17、18、19、20题10分,21、22题12分,共64分)
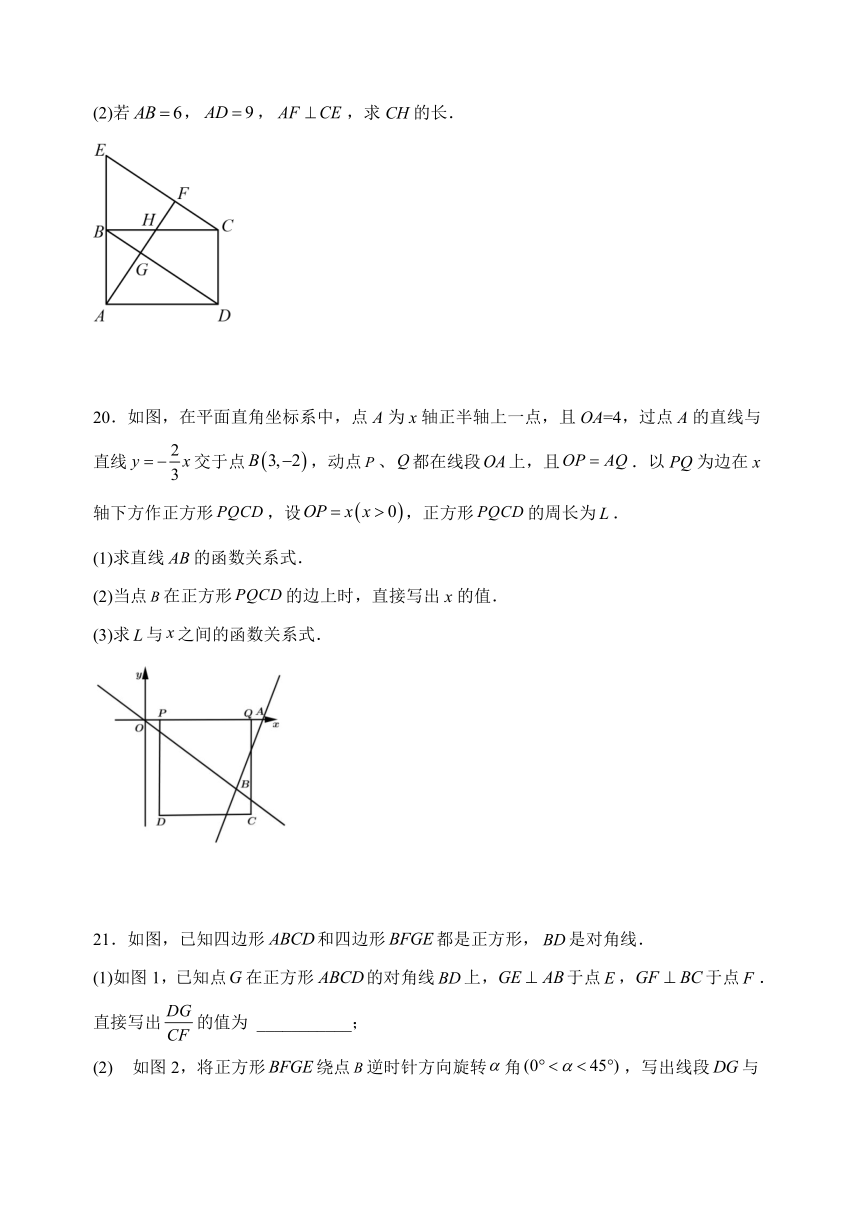
17.如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.若AD=AF,求证:四边形ABFC是矩形.
18.如图,矩形中,为上一点,交的延长线于点.
(1)求证:;
(2)若,,求的长.
19.如图,延长矩形的边到点,使,连接,是上一点,连接交于点,交于点.
(1)求证:;
(2)若,,,求CH的长.
20.如图,在平面直角坐标系中,点A为x轴正半轴上一点,且OA=4,过点A的直线与直线交于点,动点、都在线段上,且.以PQ为边在x轴下方作正方形,设,正方形的周长为.
(1)求直线的函数关系式.
(2)当点在正方形的边上时,直接写出x的值.
(3)求与之间的函数关系式.
21.如图,已知四边形和四边形都是正方形,是对角线.
(1)如图1,已知点在正方形的对角线上,于点,于点.
直接写出的值为 ___________;
如图2,将正方形绕点逆时针方向旋转角,写出线段与之间的数量关系,并证明你的结论;
(3)如图3,正方形在旋转过程中,当,,三点在一条直线上时,延长交于点.若,,直接写出正方形和正方形的边长.
*22.在矩形的边上取一点,将沿翻折,使点恰好落在边上点处.
(1)如图1,若,求的度数;
(2)如图2,当,且时,求的长;
(3)如图3,延长,与的角平分线交于点,交于点,当时,求的值.
参考答案
一、选择题
1.C 2.D 3.A 4.B 5.D 6.B 7 .C 8.D 9.D 10. A
二、填空题
11.十 12. 13.2 14. 15. 16.(1348,)
三、解答题
17.证明:在□ABCD中,AB∥DF,
∴∠ABE=∠FCE,
∵E为BC的中点,
∴BE=CE,又∠AEB=∠FEC,
∴△ABE≌△FCE(ASA).
∴AE=FE,又BE=CE,
∴四边形ABFC是平行四边形.
在□ABCD中,AD=BC,
又∵AD=AF,
∴BC=AF,
∴□ABFC是矩形.
18.(1)证明:∵四边形为矩形,
∴,,
∴.
∵,
∴,
∵,,
∴.
(2)解:∵,,
∴,
∵,
∴,即,
∴.
19.(1)四边形是矩形,
.
,
四边形是平行四边形,
,
.
(2)
,
.
.
,
,
即
,
.
20.(1)解:∵,
∴,
设直线的函数关系式为,将,代入中,
得:,解得:
∴直线的函数关系式为;
(2)①当点在正方形的边上时,则,
∴
∴,即:
此时,即点的坐标为与点重合,
②当点在正方形的边上时,
∵点为,
∴
∴,即,
③当点在正方形的边上时,则,(此时点在点的左侧)
亦即
∴
∴,
此时,即点的坐标为与点重合,
综上,当点在正方形的边上时,或3;
(3)∵,
当点在点的左侧时,即当时,,
则,
当点在点的右侧时,即当时,,
则,
综上,与之间的函数关系式为:
21.(1)解:由①知四边形是正方形,
,,
,,
,
(2)解:,理由如下:
连接,
由旋转性质知,
在和中,,,
,
,
,
线段与之间的数量关系为;
(3)解:,点、、三点共线,
,
,
,
,
,
,
,
设,则,
则由,得,
,
∴,
∴,
,
,
解得:,即,,
,
四边形是正方形,
,
综上,正方形的边长为3,正方形的边长为.
22.解:(1)将沿翻折,使点恰好落在边上点处,
,,
,
,
,
四边形是矩形,
,
,
;
(2)将沿翻折,使点恰好落在边上点处,
,,
又矩形中,,
,,
,
,
,
,
,,
,
,
,
,
,
.
(3)过点作于点,
,
,
,
,
,,
,
,
设,
平分,,,
,
设,则,
,
,
解得.
.
.
5题图
4题图
7题图
8题图
10题图
9题图
12题图
14题图
13题图
E
D
A
B
C
F
PAGE
九年级数学 (十)四边形
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )
A.6 B.11 C.12 D.18
2.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
3.菱形的两条对角线的长分别是2cm和6cm,则菱形的面积是( )
A. B. C. D.
4.如图,将一张长方形纸片按如图方式折叠,BD,BE为折痕,若∠ABE=30°,则∠DBC的度数为( ).
A. B. C. D.
5.如图,矩形ABCD的对角线AC,BD相交于点O,点E是CD的中点,若OE=3,则BC的长为( )
A.3 B.4 C.5 D.6
6.矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
A.4 B.8 C.10 D.12
7.如图,在平行四边形ABCD中,E是边上的点且,、交于点F,设的面积为,平行四边形ABCD的面积为,则的值为( )
A. B. C. D.
8.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为,点A,B,E在轴上,若正方形ABCD的边长为,则F点坐标为( )
A. B. C. D.
9.如图,在矩形中,AB=1,BC=2,对角线AC的垂直平分线分别交AD,AC于点E,O,则OE的长为( )
A. B. C. D.
10.我国汉代数学家赵爽在注解《周解算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形面积为25,小正方形面积为1,则的值为( )
A. B. C. D.
二、填空题(11-14每小题4分,15、16每小题5分,共26分)
11.若从一个多边形的一个顶点出发,最多可画7条对角线,则它是 边形.
12.如图,在菱形中,点E在上,与交于点F.若,,则 .
13.如图,在矩形ABCD中,AB=10,AD=6,矩形ABCD绕点A逆时针旋转一定角度得矩形,若点B的对应点落在边CD上,则的长为______.
14.如图,在矩形COED中,点D的坐标是,则CE的长是___________.
*15.如图,正方形ABCD中,AB=4,E点沿线段AD由A向D运动(到停止运动),F点沿线段CB由C向B运动(到B停止运动),两点同时出发,速度相同,连接EF,作BP⊥EF于P点,则在整个运动过程中P点的运动轨迹长为______.
*16.如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,若每次翻转60°,连续翻转2022次,点B的落点依次为则的坐标为___________.
三、解答题(第17、18、19、20题10分,21、22题12分,共64分)
17.如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.若AD=AF,求证:四边形ABFC是矩形.
18.如图,矩形中,为上一点,交的延长线于点.
(1)求证:;
(2)若,,求的长.
19.如图,延长矩形的边到点,使,连接,是上一点,连接交于点,交于点.
(1)求证:;
(2)若,,,求CH的长.
20.如图,在平面直角坐标系中,点A为x轴正半轴上一点,且OA=4,过点A的直线与直线交于点,动点、都在线段上,且.以PQ为边在x轴下方作正方形,设,正方形的周长为.
(1)求直线的函数关系式.
(2)当点在正方形的边上时,直接写出x的值.
(3)求与之间的函数关系式.
21.如图,已知四边形和四边形都是正方形,是对角线.
(1)如图1,已知点在正方形的对角线上,于点,于点.
直接写出的值为 ___________;
如图2,将正方形绕点逆时针方向旋转角,写出线段与之间的数量关系,并证明你的结论;
(3)如图3,正方形在旋转过程中,当,,三点在一条直线上时,延长交于点.若,,直接写出正方形和正方形的边长.
*22.在矩形的边上取一点,将沿翻折,使点恰好落在边上点处.
(1)如图1,若,求的度数;
(2)如图2,当,且时,求的长;
(3)如图3,延长,与的角平分线交于点,交于点,当时,求的值.
参考答案
一、选择题
1.C 2.D 3.A 4.B 5.D 6.B 7 .C 8.D 9.D 10. A
二、填空题
11.十 12. 13.2 14. 15. 16.(1348,)
三、解答题
17.证明:在□ABCD中,AB∥DF,
∴∠ABE=∠FCE,
∵E为BC的中点,
∴BE=CE,又∠AEB=∠FEC,
∴△ABE≌△FCE(ASA).
∴AE=FE,又BE=CE,
∴四边形ABFC是平行四边形.
在□ABCD中,AD=BC,
又∵AD=AF,
∴BC=AF,
∴□ABFC是矩形.
18.(1)证明:∵四边形为矩形,
∴,,
∴.
∵,
∴,
∵,,
∴.
(2)解:∵,,
∴,
∵,
∴,即,
∴.
19.(1)四边形是矩形,
.
,
四边形是平行四边形,
,
.
(2)
,
.
.
,
,
即
,
.
20.(1)解:∵,
∴,
设直线的函数关系式为,将,代入中,
得:,解得:
∴直线的函数关系式为;
(2)①当点在正方形的边上时,则,
∴
∴,即:
此时,即点的坐标为与点重合,
②当点在正方形的边上时,
∵点为,
∴
∴,即,
③当点在正方形的边上时,则,(此时点在点的左侧)
亦即
∴
∴,
此时,即点的坐标为与点重合,
综上,当点在正方形的边上时,或3;
(3)∵,
当点在点的左侧时,即当时,,
则,
当点在点的右侧时,即当时,,
则,
综上,与之间的函数关系式为:
21.(1)解:由①知四边形是正方形,
,,
,,
,
(2)解:,理由如下:
连接,
由旋转性质知,
在和中,,,
,
,
,
线段与之间的数量关系为;
(3)解:,点、、三点共线,
,
,
,
,
,
,
,
设,则,
则由,得,
,
∴,
∴,
,
,
解得:,即,,
,
四边形是正方形,
,
综上,正方形的边长为3,正方形的边长为.
22.解:(1)将沿翻折,使点恰好落在边上点处,
,,
,
,
,
四边形是矩形,
,
,
;
(2)将沿翻折,使点恰好落在边上点处,
,,
又矩形中,,
,,
,
,
,
,
,,
,
,
,
,
,
.
(3)过点作于点,
,
,
,
,
,,
,
,
设,
平分,,,
,
设,则,
,
,
解得.
.
.
5题图
4题图
7题图
8题图
10题图
9题图
12题图
14题图
13题图
E
D
A
B
C
F
PAGE
同课章节目录
