2024-2025北师版八年级下册数学 第六章 平行四边形 单元测试题(含答案)
文档属性
| 名称 | 2024-2025北师版八年级下册数学 第六章 平行四边形 单元测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 456.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 21:45:27 | ||
图片预览



文档简介
2024-2025北师版八下数学第六章-平行四边形-单元测试题
一、选择题( 本大共10小题, 每小题3分,共30分)
1.如图,在 ABCD中,BD为对角线,下列结论正确的是( )
A.α+β>γ B.α+β=γ
C.α+β<γ D.α+β与γ大小关系无法确定
2.若平行四边形的两条对角线长为6 cm和16 cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm B.8cm C.12cm D.16cm
3.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
4.在平面直角坐标系xOy中,平行四边形的三个顶点O(0,0),A(3,0),B(3,2),则其第四个顶点C的坐标不可能是( )
A.(0,2) B.(6,2) C.(0,﹣2) D.(4,2)
5.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.8
C.6 D.10
6.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
7.用下列一种多边形不能铺满地面的是( )
A.正方形 B.正十边形 C.正六边形 D.等边三角形
8.正n边形的一个外角为30°,则n的值为( )
A.6 B.8 C.10 D.12
9.如图,在平行四边形ABCD中,过对角线BD上任意一点P作EF∥BC,GH∥AB,且AH=2HD,若S△HDP=1,则S ABCD=( )
A.9 B. C.12 D.18
小明把一副含45°,30°的直角三角板如图摆放,
其中∠C=∠F=90°,∠A=45°,∠D=30°,
则∠α+∠β等于( )
A.280° B.285°
C.290° D.295°
二、填空题(本题共6小题,11-14每小题4分,15、16每小题5分,共26分)
11.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 米.
12.如图,平行四边形ABCD内有一点P,已知△APB、△BPC、△CPD的面积分别为4、3、1,则△APD的面积为
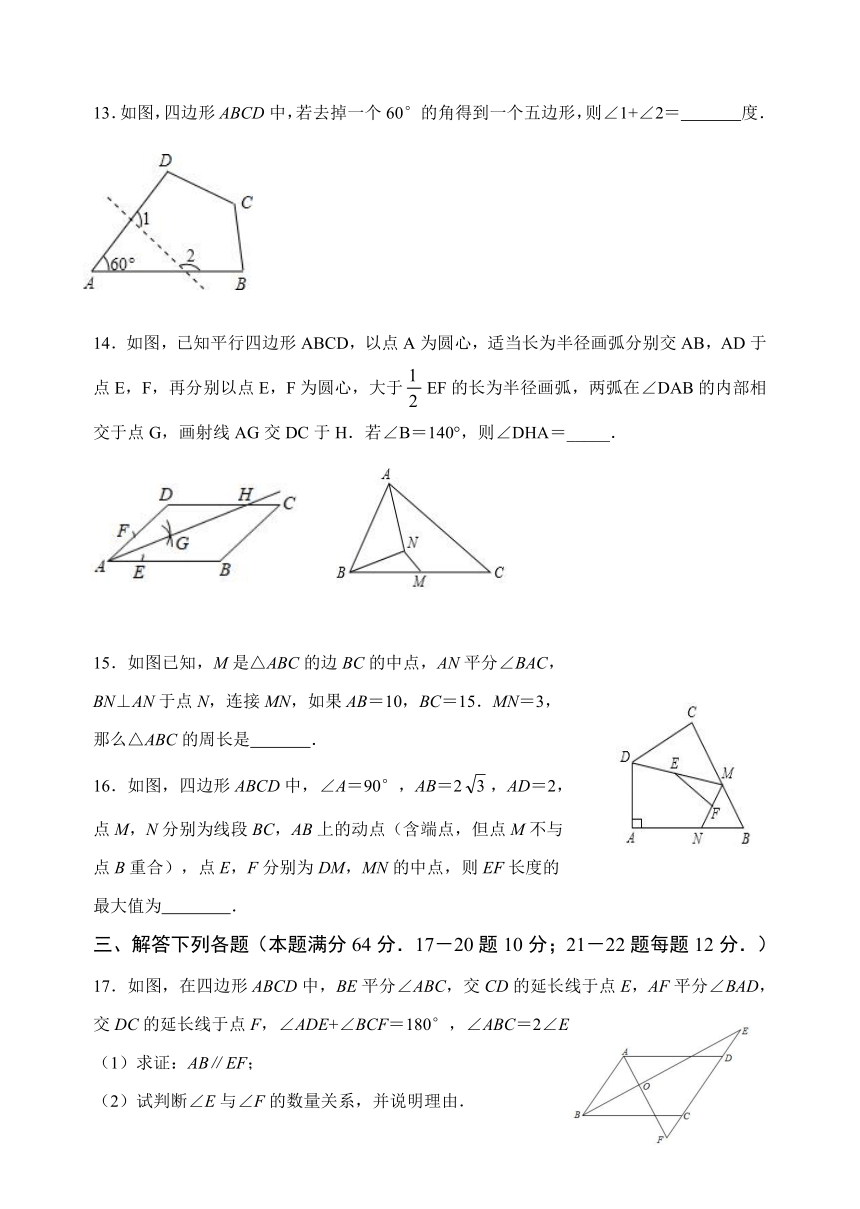
13.如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2= 度.
14.如图,已知平行四边形ABCD,以点A为圆心,适当长为半径画弧分别交AB,AD于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠DAB的内部相交于点G,画射线AG交DC于H.若∠B=140°,则∠DHA=_____.
15.如图已知,M是△ABC的边BC的中点,AN平分∠BAC,
BN⊥AN于点N,连接MN,如果AB=10,BC=15.MN=3,
那么△ABC的周长是 .
如图,四边形ABCD中,∠A=90°,AB=2,AD=2,
点M,N分别为线段BC,AB上的动点(含端点,但点M不与
点B重合),点E,F分别为DM,MN的中点,则EF长度的
最大值为 .
三、解答下列各题(本题满分64分.17-20题10分;21-22题每题12分.)
17.如图,在四边形ABCD中,BE平分∠ABC,交CD的延长线于点E,AF平分∠BAD,交DC的延长线于点F,∠ADE+∠BCF=180°,∠ABC=2∠E.
(1)求证:AB∥EF;
(2)试判断∠E与∠F的数量关系,并说明理由.
18.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.
(1)求证:DM=CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
19.如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE.
(1)若∠BCF=65°,求∠ABC的度数;
(2)求证:四边形AECF是平行四边形.
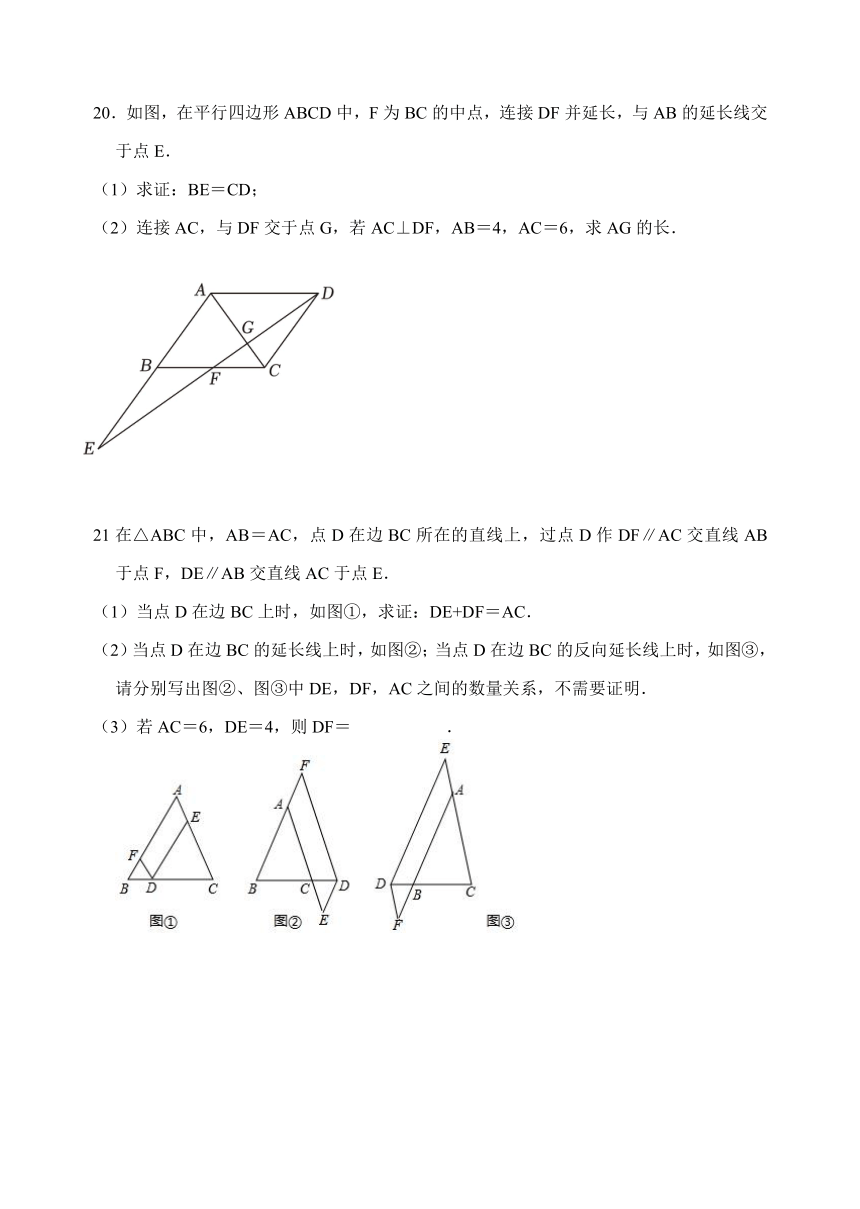
20.如图,在平行四边形ABCD中,F为BC的中点,连接DF并延长,与AB的延长线交于点E.
(1)求证:BE=CD;
(2)连接AC,与DF交于点G,若AC⊥DF,AB=4,AC=6,求AG的长.
21在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
22.如图,在平面直角坐标系中,直线l:与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
参考答案
一、选择题:(本题共10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D B B B B D D B
二、填空题(本题共6小题,11—14每小题4分,15、16每小题5分,共26分)
11. 180; 12.2; 13.240; 14.20° 15.41 16. 2;
三、解答下列各题(本题满分44分.17题每小题6分;18题6分;19题6分;20题8分;21题8分;22题10分.)
17.(1)证明:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
又∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(2)∠E+∠F=90°,理由如下:
∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC,
∴∠BAD+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=∠ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=∠ABC+∠BAD=(∠ABC+∠BAD)=×180°=90°,
由(1)知,AB∥EF,
∴∠BAF=∠F,∠ABE=∠E,
∴∠E+∠F=90°.
18. (1)证明:在△ADB和△ADE中,
∴△ADB≌△ADE(ASA)
∴AE=AB,BD=DE,
∵BD=DE,BM=MC,
∴DM=CE;
(2)解:在Rt△ADB中,AB==10,
∴AE=10,
由(1)得,CE=2DM=4,
∴AC=CE+AE=14.
19.(1)解:∵CF平分∠BCD,
∴∠BCD=2∠BCF=65°×2=130°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC=180°﹣∠BCD=180°﹣130°=50°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(ASA).
∴∠AEB=∠CFD,AE=CF,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形.
20. (1)证明:∵F为BC的中点,
∴BF=CF,
∵四边形ABCD为平行四边形,
∴CD∥AB,
∵AB的延长线为AE,
∴AE∥CD,
∴∠E=∠CDF、∠EBF=∠DCF,
∴△EBF≌△DCF(AAS),
∴BE=CD;
(2)解:∵AC⊥DF,
∴∠AGD=∠CGF=90°,
∵四边形ABCD为平行四边形,
∴AD∥BC、AD=BC,
∴∠DAG=∠FCG,
∴△AGD∽△CGF,
∴,
∵F为BC的中点,
∴,
∴,
∴,
∵AC=AG+GC=6,
∴,
∴AG=4.
21.解:(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC﹣DE=6﹣4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10
22.解:(1)
如图,过点A1作A1D⊥OM,垂足为D.
∵△A1B1C1是等边三角形,A1D⊥OM,
∴∠B1A1D=30°,
∴在Rt△A1DB1中,,
∵A1D=3,
∴在Rt△A1DB1中,,
∴,.
∴点A1的坐标为(, 3).
由直线l的解析式,得
当x=时,,
∴点A1在直线l上.
(2) ∵△A1B1C1是等边三角形,,
∴.
∴点C1的坐标为(, 0).
设直线A1C1的解析式为y=kx+b (k≠0).
将点A1 (, 3),点C1 (, 0)的坐标分别代入直线A1C1的解析式,得
,
解之,得
,
∴直线A1C1的解析式为.
(3) 点P的坐标为(, 3),(, 3)或(, -3). 求解过程如下.
根据题意,分别对下面三种情况进行讨论.
①若以∠A1C1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1MP.
如图①,过点A1作A1E⊥ON,垂足为E.
由直线l的解析式,得
当y=0时,,
∴x=.
∴点M的坐标为(, 0).
∴OM=.
∵,
∴,
∴.
∵△A1B1C1是等边三角形,
∴∠A1B1C1=60°,
∴∠A1B1E=90°-∠A1B1C1=90°-60°=30°.
∴在Rt△A1EB1中,,.
∵A1P∥C1M,A1E⊥ON,
∴点E,A1,P在同一条直线上,
∴.
∴点P的坐标为(, 3).
②若以∠A1MC1为平行四边形的一个内角,则所求平行四边形为平行四边形PC1MA1.
∵A1P∥C1M,
∴A1F⊥ON,
∴在Rt△A1FB1中,,.
∵,
∴.
∴点P的坐标为(, 3).
③若以∠C1A1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1PM.
如图③,过点P作PG⊥OM,垂足为G.
∵△A1B1C1是等边三角形,
∴∠A1C1B1=60°,
∴∠A1C1M=180°-∠A1C1B1=180°-60°=120°,
∵A1C1∥PM,
∴∠PMC1=∠A1C1M=120°,
∴∠PMG=180°-∠PMC1=180°-120°=60°,
∴在Rt△PMG中,∠MPG=90°-∠PMG=90°-60°=30°.
∵,
∴在Rt△PGM中,,
.
∵OM=,
∴.
∴点P的坐标为(, -3).
综上所述,点P的坐标为(, 3),(, 3)或(, -3).
PAGE
一、选择题( 本大共10小题, 每小题3分,共30分)
1.如图,在 ABCD中,BD为对角线,下列结论正确的是( )
A.α+β>γ B.α+β=γ
C.α+β<γ D.α+β与γ大小关系无法确定
2.若平行四边形的两条对角线长为6 cm和16 cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm B.8cm C.12cm D.16cm
3.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
4.在平面直角坐标系xOy中,平行四边形的三个顶点O(0,0),A(3,0),B(3,2),则其第四个顶点C的坐标不可能是( )
A.(0,2) B.(6,2) C.(0,﹣2) D.(4,2)
5.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.8
C.6 D.10
6.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
7.用下列一种多边形不能铺满地面的是( )
A.正方形 B.正十边形 C.正六边形 D.等边三角形
8.正n边形的一个外角为30°,则n的值为( )
A.6 B.8 C.10 D.12
9.如图,在平行四边形ABCD中,过对角线BD上任意一点P作EF∥BC,GH∥AB,且AH=2HD,若S△HDP=1,则S ABCD=( )
A.9 B. C.12 D.18
小明把一副含45°,30°的直角三角板如图摆放,
其中∠C=∠F=90°,∠A=45°,∠D=30°,
则∠α+∠β等于( )
A.280° B.285°
C.290° D.295°
二、填空题(本题共6小题,11-14每小题4分,15、16每小题5分,共26分)
11.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 米.
12.如图,平行四边形ABCD内有一点P,已知△APB、△BPC、△CPD的面积分别为4、3、1,则△APD的面积为
13.如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2= 度.
14.如图,已知平行四边形ABCD,以点A为圆心,适当长为半径画弧分别交AB,AD于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠DAB的内部相交于点G,画射线AG交DC于H.若∠B=140°,则∠DHA=_____.
15.如图已知,M是△ABC的边BC的中点,AN平分∠BAC,
BN⊥AN于点N,连接MN,如果AB=10,BC=15.MN=3,
那么△ABC的周长是 .
如图,四边形ABCD中,∠A=90°,AB=2,AD=2,
点M,N分别为线段BC,AB上的动点(含端点,但点M不与
点B重合),点E,F分别为DM,MN的中点,则EF长度的
最大值为 .
三、解答下列各题(本题满分64分.17-20题10分;21-22题每题12分.)
17.如图,在四边形ABCD中,BE平分∠ABC,交CD的延长线于点E,AF平分∠BAD,交DC的延长线于点F,∠ADE+∠BCF=180°,∠ABC=2∠E.
(1)求证:AB∥EF;
(2)试判断∠E与∠F的数量关系,并说明理由.
18.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.
(1)求证:DM=CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
19.如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE.
(1)若∠BCF=65°,求∠ABC的度数;
(2)求证:四边形AECF是平行四边形.
20.如图,在平行四边形ABCD中,F为BC的中点,连接DF并延长,与AB的延长线交于点E.
(1)求证:BE=CD;
(2)连接AC,与DF交于点G,若AC⊥DF,AB=4,AC=6,求AG的长.
21在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
22.如图,在平面直角坐标系中,直线l:与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
参考答案
一、选择题:(本题共10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D B B B B D D B
二、填空题(本题共6小题,11—14每小题4分,15、16每小题5分,共26分)
11. 180; 12.2; 13.240; 14.20° 15.41 16. 2;
三、解答下列各题(本题满分44分.17题每小题6分;18题6分;19题6分;20题8分;21题8分;22题10分.)
17.(1)证明:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
又∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(2)∠E+∠F=90°,理由如下:
∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC,
∴∠BAD+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=∠ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=∠ABC+∠BAD=(∠ABC+∠BAD)=×180°=90°,
由(1)知,AB∥EF,
∴∠BAF=∠F,∠ABE=∠E,
∴∠E+∠F=90°.
18. (1)证明:在△ADB和△ADE中,
∴△ADB≌△ADE(ASA)
∴AE=AB,BD=DE,
∵BD=DE,BM=MC,
∴DM=CE;
(2)解:在Rt△ADB中,AB==10,
∴AE=10,
由(1)得,CE=2DM=4,
∴AC=CE+AE=14.
19.(1)解:∵CF平分∠BCD,
∴∠BCD=2∠BCF=65°×2=130°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC=180°﹣∠BCD=180°﹣130°=50°;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠BAD=∠DCB,
∴∠ABE=∠CDF,
∵∠BAE=∠BAD,∠DCF=∠DCB,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(ASA).
∴∠AEB=∠CFD,AE=CF,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形.
20. (1)证明:∵F为BC的中点,
∴BF=CF,
∵四边形ABCD为平行四边形,
∴CD∥AB,
∵AB的延长线为AE,
∴AE∥CD,
∴∠E=∠CDF、∠EBF=∠DCF,
∴△EBF≌△DCF(AAS),
∴BE=CD;
(2)解:∵AC⊥DF,
∴∠AGD=∠CGF=90°,
∵四边形ABCD为平行四边形,
∴AD∥BC、AD=BC,
∴∠DAG=∠FCG,
∴△AGD∽△CGF,
∴,
∵F为BC的中点,
∴,
∴,
∴,
∵AC=AG+GC=6,
∴,
∴AG=4.
21.解:(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC﹣DE=6﹣4=2;
当如图②的情况,DF=AC+DE=6+4=10.
故答案是:2或10
22.解:(1)
如图,过点A1作A1D⊥OM,垂足为D.
∵△A1B1C1是等边三角形,A1D⊥OM,
∴∠B1A1D=30°,
∴在Rt△A1DB1中,,
∵A1D=3,
∴在Rt△A1DB1中,,
∴,.
∴点A1的坐标为(, 3).
由直线l的解析式,得
当x=时,,
∴点A1在直线l上.
(2) ∵△A1B1C1是等边三角形,,
∴.
∴点C1的坐标为(, 0).
设直线A1C1的解析式为y=kx+b (k≠0).
将点A1 (, 3),点C1 (, 0)的坐标分别代入直线A1C1的解析式,得
,
解之,得
,
∴直线A1C1的解析式为.
(3) 点P的坐标为(, 3),(, 3)或(, -3). 求解过程如下.
根据题意,分别对下面三种情况进行讨论.
①若以∠A1C1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1MP.
如图①,过点A1作A1E⊥ON,垂足为E.
由直线l的解析式,得
当y=0时,,
∴x=.
∴点M的坐标为(, 0).
∴OM=.
∵,
∴,
∴.
∵△A1B1C1是等边三角形,
∴∠A1B1C1=60°,
∴∠A1B1E=90°-∠A1B1C1=90°-60°=30°.
∴在Rt△A1EB1中,,.
∵A1P∥C1M,A1E⊥ON,
∴点E,A1,P在同一条直线上,
∴.
∴点P的坐标为(, 3).
②若以∠A1MC1为平行四边形的一个内角,则所求平行四边形为平行四边形PC1MA1.
∵A1P∥C1M,
∴A1F⊥ON,
∴在Rt△A1FB1中,,.
∵,
∴.
∴点P的坐标为(, 3).
③若以∠C1A1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1PM.
如图③,过点P作PG⊥OM,垂足为G.
∵△A1B1C1是等边三角形,
∴∠A1C1B1=60°,
∴∠A1C1M=180°-∠A1C1B1=180°-60°=120°,
∵A1C1∥PM,
∴∠PMC1=∠A1C1M=120°,
∴∠PMG=180°-∠PMC1=180°-120°=60°,
∴在Rt△PMG中,∠MPG=90°-∠PMG=90°-60°=30°.
∵,
∴在Rt△PGM中,,
.
∵OM=,
∴.
∴点P的坐标为(, -3).
综上所述,点P的坐标为(, 3),(, 3)或(, -3).
PAGE
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
