2025中考三轮数学基础知识专项训练题8图形的初步认识(含解析)
文档属性
| 名称 | 2025中考三轮数学基础知识专项训练题8图形的初步认识(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 20:46:05 | ||
图片预览




文档简介
2025中考数学基础知识专项训练题8 图形的初步认识
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
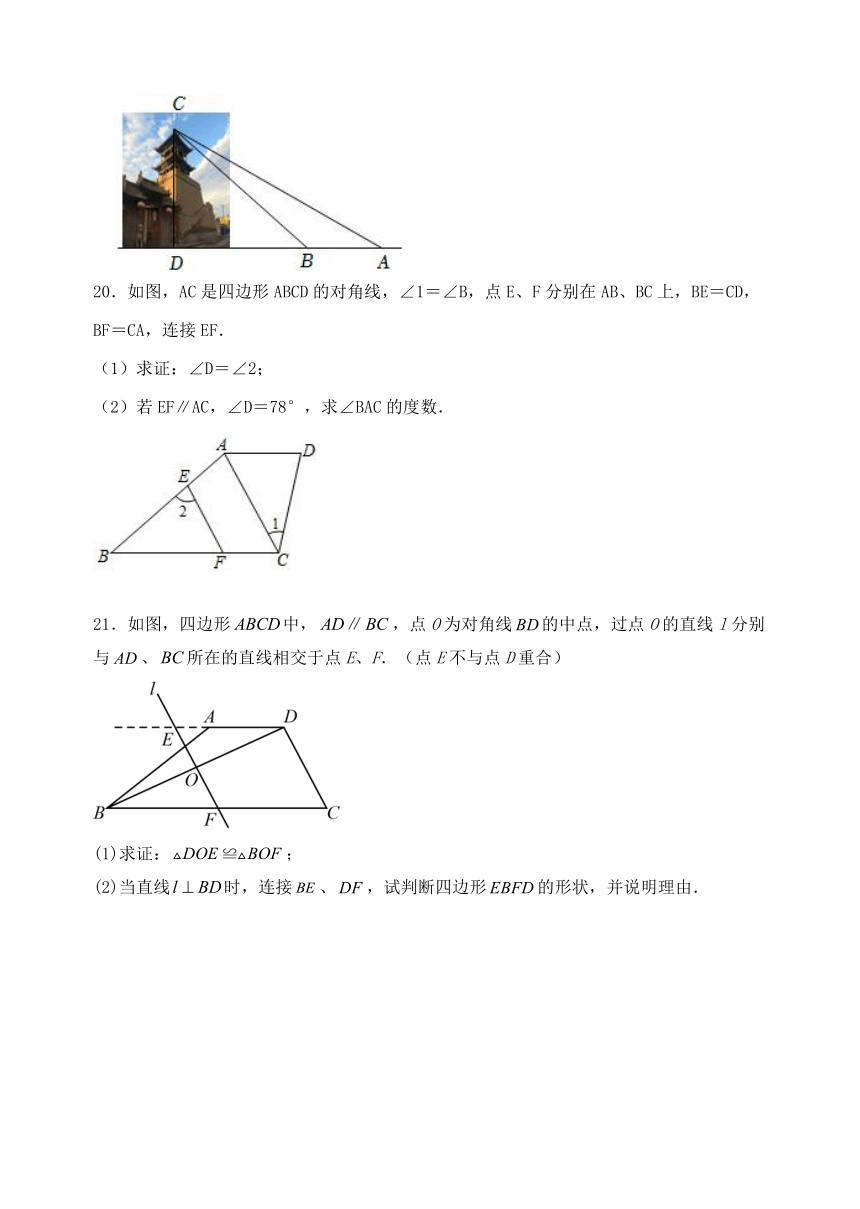
1.如图1是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )
A.面① B.面② C.面⑤ D.面⑥
如图2,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
3.榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
4.若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
5.如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B. C. D.
6.将一副三角板按图4所示摆放在一组平行线内,,,则的度数为( )
A. B. C. D.
7.如图5,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
A.两点之间,线段最短 B.两点确定一条直线
C.垂线段最短 D.三角形两边之和大于第三边
8.一个多边形的内角和为900°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
9.如图6,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
10.如图7,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )
A. B. C. D.
二、填空题(11-14每小题4分,15、16每小题5分,共26分)
11.一个多边形外角和是内角和的,则这个多边形的边数为 .
公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
12.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
13.10个棱长为1cm的正方体,摆放成如图8的形状,则这个图形的表面积为 cm2
14.如图9,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
*15.如下图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有 个
*16.有同样大小的三个立方体骰子,每个骰子的展开图如图10所示,现在把三个骰子放在桌子上(如图11),凡是能看得到的点数之和最大是 .
三、解答题(第17、18、19、20题10分, 21、22题12分,共64分)
17.计算下列各题:
(1)153°19′42″+26°40′28″;
(2)90°3″﹣57°21′44″;
(3)33°15′16″×5;
(4)175°16′30″﹣47°30′÷6+4°12′50″×3.
18.如图,某座山AB的顶部有一座通讯塔BC,且点A,B,C在同一条直线上.从地面P处测得塔顶C的仰角为42°,测得塔底B的仰角为35°.已知通讯塔BC的高度为32m,求这座山AB的高度(结果取整数).参考数据:tan35°≈0.70,tan42°≈0.90.
19.数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.41,≈1.73)
20.如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
21.如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
*22.问题提出
如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,=(n<2),延长BC至点E,点DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
参考答案与详细解析
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.下图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )
A.面① B.面② C.面⑤ D.面⑥
【答案】C
【分析】根据底面与多面体的上面是相对面,则形状相等,间隔1个长方形,且没有公共顶点,即可求解.
【详解】解:依题意,多面体的底面是面③,则多面体的上面是面⑤,
故选:C.
【点拨】本题考查了长方体的表面展开图,熟练掌握基本几何体的展开图是解题的关键.
如图,Rt△ABC是一块直角三角板,其中∠C=90°,
∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,
则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
【分析】先根据平行线的性质求得∠DAC的度数,再根据角的和差关系求得结果.
【解析】∵DE∥CB,∠C=90°,
∴∠DAC=∠C=90°,
∵∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=120°,
故答案为:B.
【点评】本题主要考查了平行线的性质以及三角形角和差计算,关键是利用平行线的性质求得∠DAC.
3.榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
【答案】C
【分析】根据主视图是从前向后观察到的图形,进行判断即可.
【详解】解:由题意,得:“卯”的主视图为:
故选:C.
【点拨】本题考查三视图,熟练掌握三视图的画法,是解题的关键.
4.若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
【分析】根据互余两角之和为90°计算即可.
【解析】∵∠A=40°,
∴∠A的余角为:90°﹣40°=50°,
故选:A.
【点评】本题考查的是余角的定义,如果两个角的和等于90°,就说这两个角互为余角.
5.如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
【分析】将矩形纸片ABCD绕边CD所在直线旋转一周,可知上面和下面都是平面,所以得到的立体图形是圆体.
【解析】根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
【点评】本题考查生活中的立体图形,理解“点动成线,线动成面,面动成体”,是正确判断的前提.
6.将一副三角板按下图所示摆放在一组平行线内,,,则的度数为( )
A. B. C. D.
【答案】C
【分析】根据两直线平行内错角相等即可求解.
【详解】解:依题意,,
∵,
∴,
故选:C.
【点拨】本题考查了平行线的性质,熟练掌握两直线平行内错角相等是解题的关键.
7.如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.三角形两边之和大于第三边
【分析】根据两点确定一条直线判断即可.
【解析】这样做应用的数学知识是两点确定一条直线,
故选:B.
【点评】本题考查的是三角形的三边关系、两点之间,线段最短、两点确定一条直线、垂线段最短,正确理解它们在实际生活中的应用是解题的关键.
8.一个多边形的内角和为900°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
【分析】根据多边形的内角和公式:(n﹣2) 180°列出方程,解方程即可得出答案.
【解析】设多边形的边数为n,(n﹣2) 180°=900°,解得:n=7.故选:A.
【点评】本题考查了多边形的内角与外角,体现了方程思想,掌握多边形的内角和=(n﹣2) 180°是解题的关键.
9.如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
【分析】过点C作水平地面的平行线,交AB的延长线于D,根据正弦的定义求出BD,根据余弦的定义求出CD,根据等腰直角三角形的性质求出AD,计算即可.
【解析】过点C作水平地面的平行线,交AB的延长线于D,
则∠BCD=α,
在Rt△BCD中,BC=m,∠BCD=α,
则BD=BC sin∠BCD=msinα,CD=BC cos∠BCD=mcosα,
在Rt△ACD中,∠ACD=45°,
则AD=CD=mcosα,
∴AB=AD﹣BD=mcosα﹣msinα=m(cosα﹣sinα),
故选:A.
10.如图,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )
A. B. C. D.
【答案】B
【分析】根据作图可得,进而逐项分析判断即可求解.
【详解】解:根据作图可得,故A,C正确;
∴在的垂直平分线上,
∴,故D选项正确,
而不一定成立,故C选项错误,
故选:B.
【点拨】本题考查了作角平分线,垂直平分线的判定,熟练掌握基本作图是解题的关键.
二、填空题(11-14每小题4分,15、16每小题5分,共26分)
11.一个多边形外角和是内角和的,则这个多边形的边数为 .
【分析】多边形的内角和定理为(n﹣2)×180°,多边形的外角和为360°,根据题意列出方程求出n的值.
【解析】设这个多边形的边数为n,
根据题意可得:,解得:n=11,故答案为:11.
【点评】本题主要考查的是多边形的内角和公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
12.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
【分析】根据菱形的面积=对角线乘积的一半,可以计算出该菱形的面积.
【解析】∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是=24(cm2),故答案为:24.
13.10个棱长为1cm的正方体,摆放成如图的形状,则这个图形的表面积为 cm2
【答案】36
【解析】解:正面有6个正方形,面积为:6×1×1=6,
上面有6个正方形,面积为:6×1×1=6,
右面有6个正方形,面积为:6×1×1=6,
∴整个几何体的表面积为:2×(6+6+6)=36.
故答案为:36.
14.如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
【分析】根据平面镜反射的规律得到∠EDO=∠CDB=20°,∠AEF=∠OED,在△ODE中,根据三角形内角和定理求出∠OED的度数,即可得到∠AEF=∠OED的度数.
【解析】∵一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,
∴∠EDO=∠CDB=20°,∠AEF=∠OED,
在△ODE中,∠OED=180°﹣∠AOB﹣∠EDO=180°﹣120°﹣20°=40°,
∴∠AEF=∠OED=40°.故答案为:40°.
【点评】本题考查了角的计算,根据平面镜反射的规律得到∠EDO=∠CDB=20°,∠AEF=∠OED是解题的关键.
*15.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有 个
【答案】91
*16.有同样大小的三个立方体骰子,每个骰子的展开图如图1所示,现在把三个骰子放在桌子上(如图2),凡是能看得到的点数之和最大是 .
【思路点拨】
观察图形可知,1和6相对、2和5相对,3和4相对;要使能看到的纸盒面上的数字之和最大,则把第一个正方体的数字1的面与第二个正方体的数字2的面相连,把数字2的面放在下面,则第一个图形露出的数字分别是3、4、5、6;第二个正方体的数字1面与第三个正方体的数字1的面相连,数字3的面放在下面,则第二个正方体露在外面的数字是4、5、6,第三个正方体露在外面的数字就是3、4、5、6,据此可得能看得到的点数之和最大值.
【解题过程】
解:根据题意得:露在外面的数字之和最大是:,
故答案为:51.
三、解答题(第17、18、19、20题10分, 21、22题12分,共64分)
17.计算下列各题:
(1)153°19′42″+26°40′28″;
(2)90°3″﹣57°21′44″;
(3)33°15′16″×5;
(4)175°16′30″﹣47°30′÷6+4°12′50″×3.
【考点】度分秒的换算.
【分析】进行度、分、秒的加法、减法.乘除法计算,度与度,分与分,秒与秒对应相加,分的结果若满60,则转化为度;度与度,分与分,秒与秒对应相乘除,分的结果若满60,则转化为度.
【解答】解:(1)153°19′42″+26°40′28″
=179°+59′+70″
=179°+60′+10″
=180°10″
(2)90°3″﹣57°21′44″
=89°59′63″﹣57°21′44″
=32°38′19″
(3)33°15′16″×5
=165°+75′+80″
=165°+76′+20″
=166°16′20″
(4)175°16′30″﹣47°30′÷6+4°12′50″×3
=175°16′30″﹣42°330′÷6+12°36′150″
=175°16′30″﹣7°﹣55′+12°38′30″
=187°54′60″﹣7°55′
=180°
【点评】此类题是进行度、分、秒的加法、减法.乘除法计算,相对比较简单,注意以60为进制即可.
18.如图,某座山AB的顶部有一座通讯塔BC,且点A,B,C在同一条直线上.从地面P处测得塔顶C的仰角为42°,测得塔底B的仰角为35°.已知通讯塔BC的高度为32m,求这座山AB的高度(结果取整数).参考数据:tan35°≈0.70,tan42°≈0.90.
【分析】设AP=x米,在Rt△APB中,利用锐角三角函数的定义求出AB的长,从而求出AC的长,然后在Rt△APC中,利用锐角三角函数的定义列出关于x的方程,进行计算即可解答.
【解析】设AP=x米,
在Rt△APB中,∠APB=35°,
∴AB=AP tan35°≈0.7x(米),
∵BC=32米,
∴AB=AB+BC=(32+0.7x)米,
在Rt△APC中,∠APC=42°,
∴tan42°==≈0.9,
∴x=160,
经检验:x=160是原方程的根,
∴AB=0.7x=112(米),
∴这座山AB的高度约为112米.
19.数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.41,≈1.73)
【分析】在Rt△BCD中,∠CBD=45°,设CD为xm,则BD=CD=xm,AD=BD+AB=(60+x)m,在Rt△ACD中,tan∠CAD=tan30°==,解方程即可.
【解析】在Rt△BCD中,∠CBD=45°,
设CD为xm,
∴BD=CD=xm,
∴AD=BD+AB=(60+x)m,
在Rt△ACD中,∠CAD=30°,
tan∠CAD=tan30°==,
解得≈82.
答:此建筑物的高度约为82 m.
20.如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
【答案】(1)证明见解析;(2)78°.
【分析】(1)由“SAS”可证△BEF≌△CDA,可得∠D=∠2;
(2)由(1)可得∠D=∠2=78°,由平行线的性质可得∠2=∠BAC=78°.
【详解】证明:(1)在△BEF和△CDA中,,∴△BEF≌△CDA(SAS),∴∠D=∠2;
(2)∵∠D=∠2,∠D=78°,∴∠D=∠2=78°,∵EF∥AC,∴∠2=∠BAC=78°.
【点睛】本题考查了全等三角形的判定与性质,平行线的性质.证明△BEF≌△CDA是解题的关键
21.如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
【答案】(1)见解析;(2)四边形为菱形;理由见解析
【解析】(1)证明:∵点O为对角线的中点,
∴,
∵,
∴,,
在和中,
,∴;
(2)解:四边形为菱形,理由如下:
连接、,如图所示:
根据解析(1)可知,,
∴,
∵,
∴四边形为平行四边形,
∵,即,
∴四边形为菱形.
*22.问题提出
如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,=(n<2),延长BC至点E,点DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
【分析】问题探究
(1)取AB的中点G,连接DG,利用等边三角形的性质可得点F为AG的中点,从而得出答案;
(2)取BC的中点H,连接DH,利用ASA证明△DBH≌△DEC,得BH=EC,则,再根据DH∥AB,得△EDH∽△EFB,从而得出答案;
问题拓展
取BC的中点H,连接DH,由(2)同理可证明△DGH≌△DEC,得GH=CE,得,再根据DH∥AB,得△EDH∽△EFB,同理可得答案.
【解析】(1)如图,取AB的中点G,连接DG,
∵点D是AC的中点,∴DG是△ABC的中位线,∴DG∥BC,∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,∵点D是AC的中点,∴∠DBC=30°,∵BD=CD,
∴∠E=∠DBC=30°,∴DF⊥AB,∵∠AGD=∠ADG=60°,∴△ADG是等边三角形,
∴AF=AG,∵AG=AB,∴AF=AB,∴;
(2)取BC的中点H,连接DH,∵点D为AC的中点,∴DH∥AB,DH=AB,
∵AB=AC,∴DH=DC,∴∠DHC=∠DCH,∵BD=DE,∴∠DBH=∠DEC,
∴∠BDH=∠EDC,∴△DBH≌△DEC(ASA),∴BH=EC,∴,∵DH∥AB,
∴△EDH∽△EFB,∴,∴,∴;
问题拓展
取BC的中点H,连接DH,
由(2)同理可证明△DGH≌△DEC(ASA),∴GH=CE,∴HE=CG,
∵=,∴,∴,∴,∵DH∥BF,∴△EDH∽△EFB,
∴,∵DH=AB,∴,∴.
【点评】本题是三角形综合题,主要考查了等腰三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,三角形中位线定理等知识,作辅助线构造三角形全等是解题的关
图2
图3
图1
图5
图4
图7
图6
图9
图8
图11
图10
PAGE
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.如图1是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )
A.面① B.面② C.面⑤ D.面⑥
如图2,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
3.榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
4.若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
5.如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B. C. D.
6.将一副三角板按图4所示摆放在一组平行线内,,,则的度数为( )
A. B. C. D.
7.如图5,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
A.两点之间,线段最短 B.两点确定一条直线
C.垂线段最短 D.三角形两边之和大于第三边
8.一个多边形的内角和为900°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
9.如图6,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
10.如图7,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )
A. B. C. D.
二、填空题(11-14每小题4分,15、16每小题5分,共26分)
11.一个多边形外角和是内角和的,则这个多边形的边数为 .
公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
12.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
13.10个棱长为1cm的正方体,摆放成如图8的形状,则这个图形的表面积为 cm2
14.如图9,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
*15.如下图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有 个
*16.有同样大小的三个立方体骰子,每个骰子的展开图如图10所示,现在把三个骰子放在桌子上(如图11),凡是能看得到的点数之和最大是 .
三、解答题(第17、18、19、20题10分, 21、22题12分,共64分)
17.计算下列各题:
(1)153°19′42″+26°40′28″;
(2)90°3″﹣57°21′44″;
(3)33°15′16″×5;
(4)175°16′30″﹣47°30′÷6+4°12′50″×3.
18.如图,某座山AB的顶部有一座通讯塔BC,且点A,B,C在同一条直线上.从地面P处测得塔顶C的仰角为42°,测得塔底B的仰角为35°.已知通讯塔BC的高度为32m,求这座山AB的高度(结果取整数).参考数据:tan35°≈0.70,tan42°≈0.90.
19.数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.41,≈1.73)
20.如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
21.如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
*22.问题提出
如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,=(n<2),延长BC至点E,点DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
参考答案与详细解析
本试卷分A类和B类,满分120分;考试时间90分钟.其中A类19个题,B类(标有*)3个题.
一、选择题(每小题3分,共30分)
1.下图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是( )
A.面① B.面② C.面⑤ D.面⑥
【答案】C
【分析】根据底面与多面体的上面是相对面,则形状相等,间隔1个长方形,且没有公共顶点,即可求解.
【详解】解:依题意,多面体的底面是面③,则多面体的上面是面⑤,
故选:C.
【点拨】本题考查了长方体的表面展开图,熟练掌握基本几何体的展开图是解题的关键.
如图,Rt△ABC是一块直角三角板,其中∠C=90°,
∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,
则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
【分析】先根据平行线的性质求得∠DAC的度数,再根据角的和差关系求得结果.
【解析】∵DE∥CB,∠C=90°,
∴∠DAC=∠C=90°,
∵∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=120°,
故答案为:B.
【点评】本题主要考查了平行线的性质以及三角形角和差计算,关键是利用平行线的性质求得∠DAC.
3.榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
【答案】C
【分析】根据主视图是从前向后观察到的图形,进行判断即可.
【详解】解:由题意,得:“卯”的主视图为:
故选:C.
【点拨】本题考查三视图,熟练掌握三视图的画法,是解题的关键.
4.若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
【分析】根据互余两角之和为90°计算即可.
【解析】∵∠A=40°,
∴∠A的余角为:90°﹣40°=50°,
故选:A.
【点评】本题考查的是余角的定义,如果两个角的和等于90°,就说这两个角互为余角.
5.如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
【分析】将矩形纸片ABCD绕边CD所在直线旋转一周,可知上面和下面都是平面,所以得到的立体图形是圆体.
【解析】根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
【点评】本题考查生活中的立体图形,理解“点动成线,线动成面,面动成体”,是正确判断的前提.
6.将一副三角板按下图所示摆放在一组平行线内,,,则的度数为( )
A. B. C. D.
【答案】C
【分析】根据两直线平行内错角相等即可求解.
【详解】解:依题意,,
∵,
∴,
故选:C.
【点拨】本题考查了平行线的性质,熟练掌握两直线平行内错角相等是解题的关键.
7.如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.三角形两边之和大于第三边
【分析】根据两点确定一条直线判断即可.
【解析】这样做应用的数学知识是两点确定一条直线,
故选:B.
【点评】本题考查的是三角形的三边关系、两点之间,线段最短、两点确定一条直线、垂线段最短,正确理解它们在实际生活中的应用是解题的关键.
8.一个多边形的内角和为900°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
【分析】根据多边形的内角和公式:(n﹣2) 180°列出方程,解方程即可得出答案.
【解析】设多边形的边数为n,(n﹣2) 180°=900°,解得:n=7.故选:A.
【点评】本题考查了多边形的内角与外角,体现了方程思想,掌握多边形的内角和=(n﹣2) 180°是解题的关键.
9.如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
【分析】过点C作水平地面的平行线,交AB的延长线于D,根据正弦的定义求出BD,根据余弦的定义求出CD,根据等腰直角三角形的性质求出AD,计算即可.
【解析】过点C作水平地面的平行线,交AB的延长线于D,
则∠BCD=α,
在Rt△BCD中,BC=m,∠BCD=α,
则BD=BC sin∠BCD=msinα,CD=BC cos∠BCD=mcosα,
在Rt△ACD中,∠ACD=45°,
则AD=CD=mcosα,
∴AB=AD﹣BD=mcosα﹣msinα=m(cosα﹣sinα),
故选:A.
10.如图,用直尺和圆规作的角平分线,根据作图痕迹,下列结论不一定正确的是( )
A. B. C. D.
【答案】B
【分析】根据作图可得,进而逐项分析判断即可求解.
【详解】解:根据作图可得,故A,C正确;
∴在的垂直平分线上,
∴,故D选项正确,
而不一定成立,故C选项错误,
故选:B.
【点拨】本题考查了作角平分线,垂直平分线的判定,熟练掌握基本作图是解题的关键.
二、填空题(11-14每小题4分,15、16每小题5分,共26分)
11.一个多边形外角和是内角和的,则这个多边形的边数为 .
【分析】多边形的内角和定理为(n﹣2)×180°,多边形的外角和为360°,根据题意列出方程求出n的值.
【解析】设这个多边形的边数为n,
根据题意可得:,解得:n=11,故答案为:11.
【点评】本题主要考查的是多边形的内角和公式以及外角和定理,属于基础题型.记忆理解并应用这两个公式是解题的关键.
12.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
【分析】根据菱形的面积=对角线乘积的一半,可以计算出该菱形的面积.
【解析】∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是=24(cm2),故答案为:24.
13.10个棱长为1cm的正方体,摆放成如图的形状,则这个图形的表面积为 cm2
【答案】36
【解析】解:正面有6个正方形,面积为:6×1×1=6,
上面有6个正方形,面积为:6×1×1=6,
右面有6个正方形,面积为:6×1×1=6,
∴整个几何体的表面积为:2×(6+6+6)=36.
故答案为:36.
14.如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
【分析】根据平面镜反射的规律得到∠EDO=∠CDB=20°,∠AEF=∠OED,在△ODE中,根据三角形内角和定理求出∠OED的度数,即可得到∠AEF=∠OED的度数.
【解析】∵一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,
∴∠EDO=∠CDB=20°,∠AEF=∠OED,
在△ODE中,∠OED=180°﹣∠AOB﹣∠EDO=180°﹣120°﹣20°=40°,
∴∠AEF=∠OED=40°.故答案为:40°.
【点评】本题考查了角的计算,根据平面镜反射的规律得到∠EDO=∠CDB=20°,∠AEF=∠OED是解题的关键.
*15.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有 个
【答案】91
*16.有同样大小的三个立方体骰子,每个骰子的展开图如图1所示,现在把三个骰子放在桌子上(如图2),凡是能看得到的点数之和最大是 .
【思路点拨】
观察图形可知,1和6相对、2和5相对,3和4相对;要使能看到的纸盒面上的数字之和最大,则把第一个正方体的数字1的面与第二个正方体的数字2的面相连,把数字2的面放在下面,则第一个图形露出的数字分别是3、4、5、6;第二个正方体的数字1面与第三个正方体的数字1的面相连,数字3的面放在下面,则第二个正方体露在外面的数字是4、5、6,第三个正方体露在外面的数字就是3、4、5、6,据此可得能看得到的点数之和最大值.
【解题过程】
解:根据题意得:露在外面的数字之和最大是:,
故答案为:51.
三、解答题(第17、18、19、20题10分, 21、22题12分,共64分)
17.计算下列各题:
(1)153°19′42″+26°40′28″;
(2)90°3″﹣57°21′44″;
(3)33°15′16″×5;
(4)175°16′30″﹣47°30′÷6+4°12′50″×3.
【考点】度分秒的换算.
【分析】进行度、分、秒的加法、减法.乘除法计算,度与度,分与分,秒与秒对应相加,分的结果若满60,则转化为度;度与度,分与分,秒与秒对应相乘除,分的结果若满60,则转化为度.
【解答】解:(1)153°19′42″+26°40′28″
=179°+59′+70″
=179°+60′+10″
=180°10″
(2)90°3″﹣57°21′44″
=89°59′63″﹣57°21′44″
=32°38′19″
(3)33°15′16″×5
=165°+75′+80″
=165°+76′+20″
=166°16′20″
(4)175°16′30″﹣47°30′÷6+4°12′50″×3
=175°16′30″﹣42°330′÷6+12°36′150″
=175°16′30″﹣7°﹣55′+12°38′30″
=187°54′60″﹣7°55′
=180°
【点评】此类题是进行度、分、秒的加法、减法.乘除法计算,相对比较简单,注意以60为进制即可.
18.如图,某座山AB的顶部有一座通讯塔BC,且点A,B,C在同一条直线上.从地面P处测得塔顶C的仰角为42°,测得塔底B的仰角为35°.已知通讯塔BC的高度为32m,求这座山AB的高度(结果取整数).参考数据:tan35°≈0.70,tan42°≈0.90.
【分析】设AP=x米,在Rt△APB中,利用锐角三角函数的定义求出AB的长,从而求出AC的长,然后在Rt△APC中,利用锐角三角函数的定义列出关于x的方程,进行计算即可解答.
【解析】设AP=x米,
在Rt△APB中,∠APB=35°,
∴AB=AP tan35°≈0.7x(米),
∵BC=32米,
∴AB=AB+BC=(32+0.7x)米,
在Rt△APC中,∠APC=42°,
∴tan42°==≈0.9,
∴x=160,
经检验:x=160是原方程的根,
∴AB=0.7x=112(米),
∴这座山AB的高度约为112米.
19.数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.41,≈1.73)
【分析】在Rt△BCD中,∠CBD=45°,设CD为xm,则BD=CD=xm,AD=BD+AB=(60+x)m,在Rt△ACD中,tan∠CAD=tan30°==,解方程即可.
【解析】在Rt△BCD中,∠CBD=45°,
设CD为xm,
∴BD=CD=xm,
∴AD=BD+AB=(60+x)m,
在Rt△ACD中,∠CAD=30°,
tan∠CAD=tan30°==,
解得≈82.
答:此建筑物的高度约为82 m.
20.如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
【答案】(1)证明见解析;(2)78°.
【分析】(1)由“SAS”可证△BEF≌△CDA,可得∠D=∠2;
(2)由(1)可得∠D=∠2=78°,由平行线的性质可得∠2=∠BAC=78°.
【详解】证明:(1)在△BEF和△CDA中,,∴△BEF≌△CDA(SAS),∴∠D=∠2;
(2)∵∠D=∠2,∠D=78°,∴∠D=∠2=78°,∵EF∥AC,∴∠2=∠BAC=78°.
【点睛】本题考查了全等三角形的判定与性质,平行线的性质.证明△BEF≌△CDA是解题的关键
21.如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
【答案】(1)见解析;(2)四边形为菱形;理由见解析
【解析】(1)证明:∵点O为对角线的中点,
∴,
∵,
∴,,
在和中,
,∴;
(2)解:四边形为菱形,理由如下:
连接、,如图所示:
根据解析(1)可知,,
∴,
∵,
∴四边形为平行四边形,
∵,即,
∴四边形为菱形.
*22.问题提出
如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,=(n<2),延长BC至点E,点DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
【分析】问题探究
(1)取AB的中点G,连接DG,利用等边三角形的性质可得点F为AG的中点,从而得出答案;
(2)取BC的中点H,连接DH,利用ASA证明△DBH≌△DEC,得BH=EC,则,再根据DH∥AB,得△EDH∽△EFB,从而得出答案;
问题拓展
取BC的中点H,连接DH,由(2)同理可证明△DGH≌△DEC,得GH=CE,得,再根据DH∥AB,得△EDH∽△EFB,同理可得答案.
【解析】(1)如图,取AB的中点G,连接DG,
∵点D是AC的中点,∴DG是△ABC的中位线,∴DG∥BC,∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,∵点D是AC的中点,∴∠DBC=30°,∵BD=CD,
∴∠E=∠DBC=30°,∴DF⊥AB,∵∠AGD=∠ADG=60°,∴△ADG是等边三角形,
∴AF=AG,∵AG=AB,∴AF=AB,∴;
(2)取BC的中点H,连接DH,∵点D为AC的中点,∴DH∥AB,DH=AB,
∵AB=AC,∴DH=DC,∴∠DHC=∠DCH,∵BD=DE,∴∠DBH=∠DEC,
∴∠BDH=∠EDC,∴△DBH≌△DEC(ASA),∴BH=EC,∴,∵DH∥AB,
∴△EDH∽△EFB,∴,∴,∴;
问题拓展
取BC的中点H,连接DH,
由(2)同理可证明△DGH≌△DEC(ASA),∴GH=CE,∴HE=CG,
∵=,∴,∴,∴,∵DH∥BF,∴△EDH∽△EFB,
∴,∵DH=AB,∴,∴.
【点评】本题是三角形综合题,主要考查了等腰三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,三角形中位线定理等知识,作辅助线构造三角形全等是解题的关
图2
图3
图1
图5
图4
图7
图6
图9
图8
图11
图10
PAGE
同课章节目录
