沪教版(五四学制)八年级数学下册 12.1 多边形 练习(含详解)
文档属性
| 名称 | 沪教版(五四学制)八年级数学下册 12.1 多边形 练习(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 726.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-13 00:00:00 | ||
图片预览



文档简介
第二十二章 第一节 多边形
一、单选题
1.下列说法中,正确的有( )
①由几条线段连接起来组成的图形叫多边形;
②三角形是边数最少的多边形;
③n边形有n条边、n个顶点.
A.0个 B.1个 C.2个 D.3个
2.一个多边形的每个内角都等于144°,则这个多边形是( )
A.八边形 B.九边形 C.十边形 D.十一边形
3.一个多边形的内角和是外角的2倍,则这个多边形共有( )对角线
A.0条 B.2条 C.5条 D.9条
4.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )
A.正方形 B.正六边形 C.正八边形 D.正十边形
5.一个正多边形的每个外角都等于40°,则它的内角和是( )
A. B. C. D.
6.下列正多边形的组合中,能够铺满地面不留缝隙的是( ).
A.正六边形和正五边形 B.正八边形和正三角形
C.正五边形和正八边形 D.正六边形和正三角形
7.一个多边形除了一个内角外,其余各内角的和为2000°,则这个内角是( ).
A.160° B.140° C.200° D.20°
8.一个多边形剪去一个角后,所得多边形的内角和是,则这个多边形的边数不可能是( )
A.4 B.5 C.6 D.7
9.如图,从一个四边形的同一个顶点出发可以引出1条对角线,从五边形的同一个顶点出发,可以引出2条对角线,从六边形的同一个顶点出发,可以引出3条对角线,……,依此规律,从n边形的同一个顶点出发,可以引出的对角线数量为( )
A.n B. C. D.
10.图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
二、填空题
11.在同一平面内,由 图形叫多边形.组成多边形的线段叫做 ,相邻两边的公共端点叫多边形的 .如果一个多边形有n条边,那么这个多边形叫做 .多边形 叫做它的内角,多边形的边与它邻边 组成的角叫多边形的外角.连接多边形 的线段叫做多边形的对角线.
12.如果一个多边形的内角和等于它的外角和5倍,那么这个多边形是 边形.
13.多边形的边数每增加1,它的内角和就增加 ,外角和 .
14.在一张凸n边形纸片上剪去一个三角形纸片,得到一个内角和为的凸多边形纸片,则n的值为 .
15.有一锐角为的直角三角形纸片,现过斜边上一点与斜边垂直的方向将其剪开,分成三角形和四边形两部分,则在四边形中,最大角的度数是 .
16.如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.,则= .
17.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,外角∠1,∠2,∠3,∠4的和等于220°,则∠BOD的度数是 度.
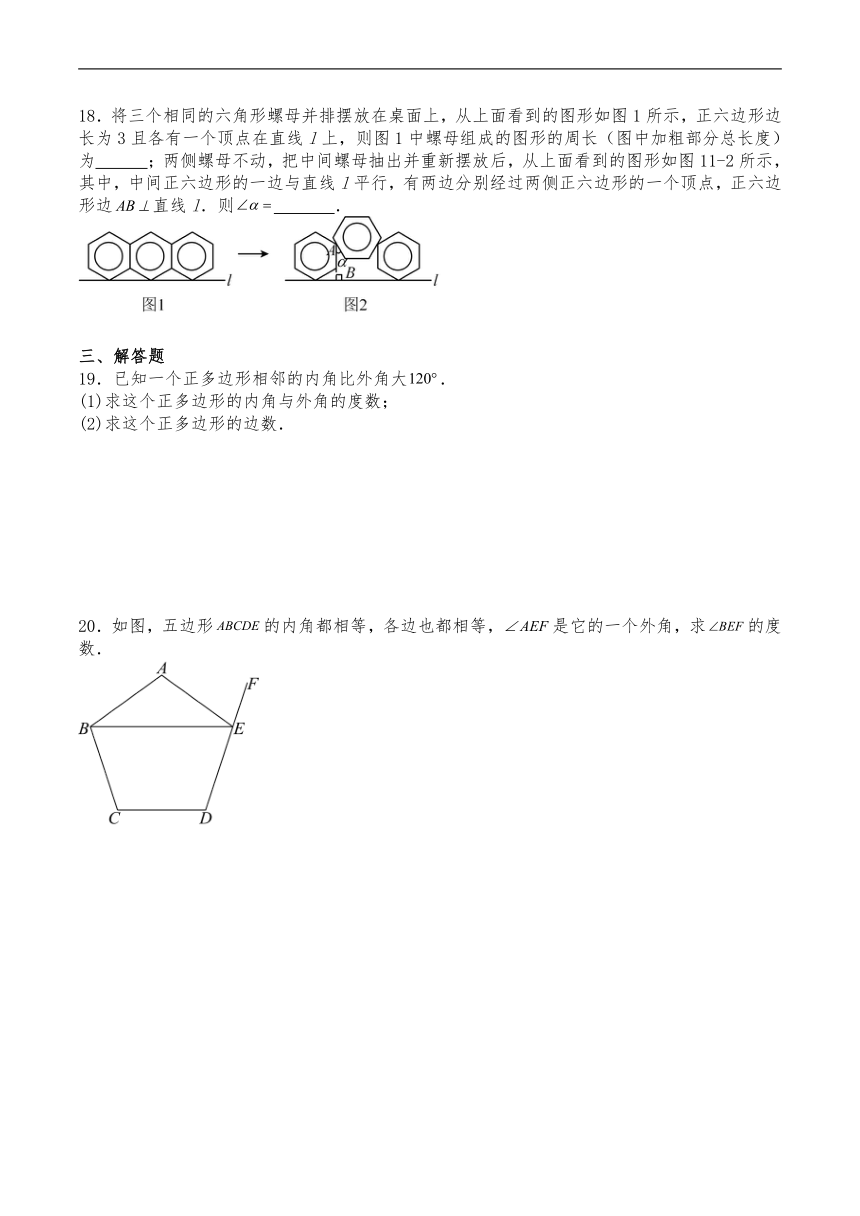
18.将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为3且各有一个顶点在直线l上,则图1中螺母组成的图形的周长(图中加粗部分总长度)为 ;两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图11-2所示,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线l.则 .
三、解答题
19.已知一个正多边形相邻的内角比外角大.
(1)求这个正多边形的内角与外角的度数;
(2)求这个正多边形的边数.
20.如图,五边形的内角都相等,各边也都相等,是它的一个外角,求的度数.
21.如图,为正五边形.
(1)求的度数;
(2)连接,求证:.
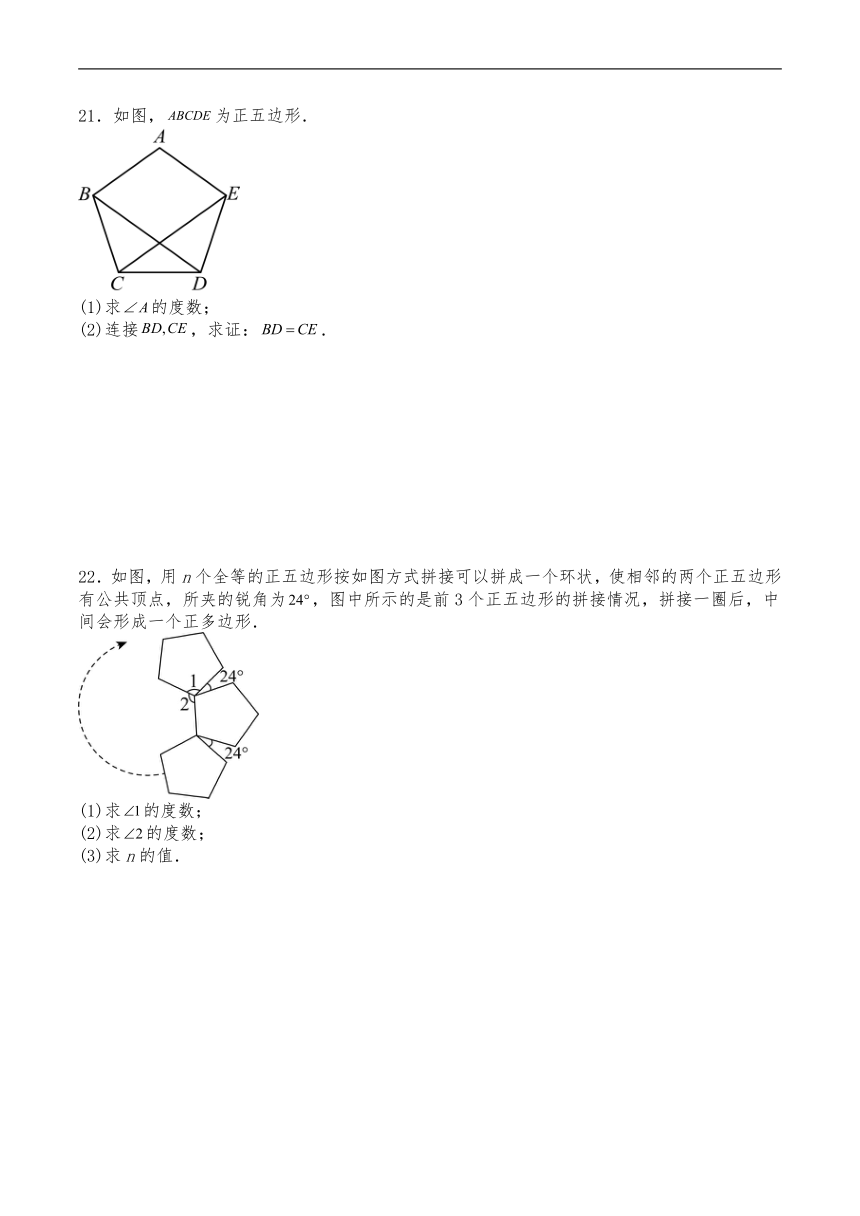
22.如图,用n个全等的正五边形按如图方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形.
(1)求的度数;
(2)求的度数;
(3)求n的值.
23.如图,在平面直角坐标系中,,,, .
(1)求证:;
(2)求证:;
(3)求四边形的面积.
24.和分别是两个多边形,阅读和的对话,完成下列各小题.
(1)嘉嘉说:“因为的边数比多,所以的外角和比的大,”判断嘉嘉的说法是否正确?并说明理由;
(2)设的边数为
①若,求的值;
②淇淇说:“无论取何值,的值始终不变.”请用列方程的方法说明理由.
25.探究归纳题:
(1)如图1,经过四边形的一个顶点可以作 条对角线,它把四边形分成 个三角形;
(2)如图2,经过五边形的一个顶点可以作 条对角线,它把五边形分成 个三角形;
(3)探索归纳:对于边形,过一个顶点可以作 条对角线,它把边形分成 个三角形;(用含的式子表示)
(4)如果经过多边形的一个顶点可以作100条对角线,那么这个多边形的边数为 .
答案
一、单选题
1.C
【分析】根据多边形的定义判断即可.
【解析】由一些线段首尾顺次相接组成的封闭图形叫做多边形,①不正确;易知②③正确,
故选:C.
2.C
【分析】先求出每一个外角的度数,再根据边数=360°÷外角的度数计算即可.
【解析】解:180°-144°=36°,
360°÷36°=10,
∴这个多边形的边数是10.
故选:C.
3.D
【分析】先根据该多边形的内角和是外角和2倍,可得出:(n-2) 180=360×2,求出多边形的边数n,再根据n边形对角线的总条数为:,求解即可.
【解析】设这个多边形有n条边,由题意得:
(n 2)×180=360×2,
解得:n=6,
从这个多边形的对角线的条数是=9,故D正确.
故选:D.
4.C
【分析】设这个外角是x°,则内角是3x°,根据内角与它相邻的外角互补列出方程求出外角的度数,根据多边形的外角和是360°即可求解.
【解析】解:∵一个正多边形每个内角与它相邻外角的度数比为3:1,
∴设这个外角是x°,则内角是3x°,
根据题意得:x+3x=180°,
解得:x=45°,
360°÷45°=8(边),
故选:C.
5.C
【分析】先根据多边形的外角和求多边形的边数,再根据多边形的内角和公式求出即可.
【解析】解:设这个多边形是n边形,根据多边形的外角和为360°可得,40°×n=360°,
解得n=9.
所以这个多边形的内角和为(9-2)×180°=1260°.
故选C.
6.D
【分析】正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
【解析】解:A.正六边形的每个内角是120°,正五边形每个内角是180°-360°÷5=108°,120m+108n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
B.正八边形的每个内角为:180°-360°÷8=135°,正三角形的每个内角60°.135m+60n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
C.正五边形每个内角是180°-360°÷5=108°,正八边形的每个内角为:180°-360°÷8=135°,108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
D.正六边形的每个内角是180°-360°÷6=120°,正三角形的每个内角是60°,2×120°+2×60°=360°,或120°+4×60°=360度,能铺满;
故选:D.
7.A
【分析】设多边形的边数是n,没加的内角为x,根据多边形的内角和公式,进行计算即可得解.
【解析】解:设多边形的边数是n,没加的内角为x,
根据题意得:,
∵,
∴,.
故选:A.
8.A
【分析】根据多边形的内角和求出剪去一个角后的多边形的边数即可判断.
【解析】解:由题意得,
,解得,
由于剪去一个角后边数为6,则这个多边形不可能为四边形,
故选A.
9.C
【分析】根据题意可得从n边型的同一个顶点出发,可以引条对角线.
【解析】解:∵从一个四边形的同一个顶点出发可以引出条对角线;
从五边形的同一个顶点出发,可以引出条对角线,
从六边形的同一个顶点出发,可以引出条对角线,
∴从n边型的同一个顶点出发,可以引条对角线,
故选:C.
10.C
【分析】本题只看图觉得很复杂,但从数据入手,就简单了,从图2开始,每个图都比前一个图多360度.抓住这点就很容易解决问题了.
【解析】解:依题意可知,二环三角形,S=360度;
二环四边形,S=720=360×2=360×(4﹣2)度;
二环五边形,S=1080=360×3=360×(5﹣2)度;
…
∴二环十边形,S=360×(10﹣2)=2880度.
故选:C.
二、填空题
11. 不在同一条直线上的n()条线段首尾顺次连接组成的 多边形的边 顶点 n边形 相邻两边组成的角 延长线 不相邻两个顶点
【分析】利用多边形定义、多边形内角、多边形外角及多边形对角线定义填空即可.
【解析】在同一平面内,由不在同一条直线上的n()条线段首尾顺次连接组成的图形叫多边形.
组成多边形的线段叫做多边形的边,
相邻两边的公共端点叫多边形的顶点.
如果一个多边形有n条边,那么这个多边形叫做n边形.
多边形相邻两边组成的角叫做它的内角,
多边形的边与它邻边延长线组成的角叫多边形的外角.
连接多边形不相邻两个顶点的线段叫做多边形的对角线.
故答案为:不在同一条直线上的n()条线段首尾顺次连接组成的;多边形的边;顶点;n边形;相邻两边组成的角;延长线;不相邻两个顶点.
12.十二
【解析】设此多边形有n条边,
根据题意得:(n-2)·180°=5×360°,
解得n=12.
故答案为12.
13. 180° 不变
【分析】多边形的内角和定理:n边形的内角和是(n-2)·180°(n≥3,且n为正数);所以当边数加1,内角和增加180°,任何多边形的外角和都是360°.
【解析】根据多边形的内角和定理,多边形的边数每增加1,它的内角和就增加180°;
任何多边形的外角和都是360°,所以外角和不变.
故答案为180°;不变.
14.5或6或7
【分析】本题考查多边形内角和定理、剪纸问题,掌握多边形的内角和定理及分类讨论问题是解题的关键.设剪去一个角后的多边形边数为n,利用多边形内角和公式则有,解出方程就可以得到新多边形的边数;然后通过分析当沿的是对角线和沿的不是对角线这两种方式剪角,就可以求出原来多边形的边数.
【解析】解:设内角和为的多边形的边数为n,则,
解得,
即得到的多边形是6边形,
当沿的是一条对角线剪去一个角,则原来的是7边形,
当沿的直线并不是对角线时,分为两种情况:
①过多边形的一个顶点,则原来的是6边形;
②不过多边形的顶点,则原来的是5边形,
综上所述,原多边形的边数为5或6或7,
故答案为:5或6或7.
15.
【分析】分两种情况分别画出图形,根据直角三角形各角的度数和四边形内角和进行求解,最后通过比较即可得出最大角的度数.本题主要考查了四边形的内角和,分类讨论和正确画出图形是解题的关键.
【解析】解:如图1所示,在中,,, 于点D,则,
∴,
如图2所示,在中,,, 于点D,则,
∴,
∵,
∴在四边形中,最大角的度数是.
故答案为:
16.
【分析】利用多边形的外角和定理,即减去等边三角形的一个内角的度数,减去正五边形的一个内角的度数,减去正方形的一个内角的度数,再减去和的度数,最后得出答案.
【解析】等边三角形的内角的度数是,正方形的内角的度数为,正五边形的内角的度数是,
则.
故答案为:
17.40.
【分析】在DO延长线上找一点M,根据多边形的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【解析】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∴∠BOM=360°﹣220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°﹣∠BOM=180°﹣140°=40°.
故答案为:40
18.
【分析】题考查正六边形的特征,解题的关键是掌握正六边形的每个外角都是.
(1)运用组成图形的边的数量和乘以边长解题即可;
(2)根据六边形的外角和平行线的性质解题即可.
【解析】解:图1中螺母组成的图形的周长为:;
如图,延长交直线l于点C,延长交于点F,
∵直线l,
∴,
又∵,
∴,即,
又∵图形是正六边形,
∴,
∴,
故答案为:;.
三、解答题
19.(1)设正多边形的外角为,则内角为,由题意,得
,
解得.
正多边形的内角为,外角为.
(2)这个正多边形的边数为:.
20.解:∵五边形的内角都相等,
∴五边形的外角都相等,
∴,
∴五边形的每个内角度数为:,
∵,
∴,
∴.
21.(1)解:∵正五边形的每一个内角的度数为:,
∴;
(2)解:∵五边形是正五边形,
∴,,
∴在和中,
,
∴,
∴.
22.(1)解:正五边形内角和为,
故;
(2)解:∵,
∴;
(3)解:由题意得:,
解得:.
23.(1)解:如图:在四边形中,
,
,
,
,
,
,
又,
.
(2)解:如图2,过点A作于点,作的延长线于点E,
,,,
,,
,
又,
,
又∵AF⊥BC,,
,,
,
,
.
(3)解:如图2:作轴于点.
,,,
.
,.
.
24.(1)解:嘉嘉的说法不正确;
理由:多边形的外角和始终为,与多边形的边数无关;
(2)①,
解得,
即的值为;
②,
整理得,
解得.
∴无论取何值,的值始终不变.
25.(1)如图1:
经过1个顶点做1条对角线,它把四边形分为2个三角形,
故答案为:1,2
(2)如图2:
经过五边形一个顶点,共有2条对角线,将这个多边形分为3个三角形;
故答案为:2,3.
(3)∵经过四边形的一个顶点可以作条对角线,它把四边形分成个三角形;
经过五边形的一个顶点可以作条对角线,它把五边形分成个三角形;
经过六边形的一个顶点可以作条对角线,它把六边形分成个三角形;
经过七边形的一个顶点可以作条对角线,它把七边形分成个三角形;
……
∴经过n边形的一个顶点可以作条对角线,它把n边形分成个三角形;
故答案为:,.
(4)∵过多边形的一个顶点可以作100条对角线,
∴根据(3)中结论可得,,
∴,
故答案为:103.
一、单选题
1.下列说法中,正确的有( )
①由几条线段连接起来组成的图形叫多边形;
②三角形是边数最少的多边形;
③n边形有n条边、n个顶点.
A.0个 B.1个 C.2个 D.3个
2.一个多边形的每个内角都等于144°,则这个多边形是( )
A.八边形 B.九边形 C.十边形 D.十一边形
3.一个多边形的内角和是外角的2倍,则这个多边形共有( )对角线
A.0条 B.2条 C.5条 D.9条
4.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )
A.正方形 B.正六边形 C.正八边形 D.正十边形
5.一个正多边形的每个外角都等于40°,则它的内角和是( )
A. B. C. D.
6.下列正多边形的组合中,能够铺满地面不留缝隙的是( ).
A.正六边形和正五边形 B.正八边形和正三角形
C.正五边形和正八边形 D.正六边形和正三角形
7.一个多边形除了一个内角外,其余各内角的和为2000°,则这个内角是( ).
A.160° B.140° C.200° D.20°
8.一个多边形剪去一个角后,所得多边形的内角和是,则这个多边形的边数不可能是( )
A.4 B.5 C.6 D.7
9.如图,从一个四边形的同一个顶点出发可以引出1条对角线,从五边形的同一个顶点出发,可以引出2条对角线,从六边形的同一个顶点出发,可以引出3条对角线,……,依此规律,从n边形的同一个顶点出发,可以引出的对角线数量为( )
A.n B. C. D.
10.图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
二、填空题
11.在同一平面内,由 图形叫多边形.组成多边形的线段叫做 ,相邻两边的公共端点叫多边形的 .如果一个多边形有n条边,那么这个多边形叫做 .多边形 叫做它的内角,多边形的边与它邻边 组成的角叫多边形的外角.连接多边形 的线段叫做多边形的对角线.
12.如果一个多边形的内角和等于它的外角和5倍,那么这个多边形是 边形.
13.多边形的边数每增加1,它的内角和就增加 ,外角和 .
14.在一张凸n边形纸片上剪去一个三角形纸片,得到一个内角和为的凸多边形纸片,则n的值为 .
15.有一锐角为的直角三角形纸片,现过斜边上一点与斜边垂直的方向将其剪开,分成三角形和四边形两部分,则在四边形中,最大角的度数是 .
16.如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.,则= .
17.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,外角∠1,∠2,∠3,∠4的和等于220°,则∠BOD的度数是 度.
18.将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为3且各有一个顶点在直线l上,则图1中螺母组成的图形的周长(图中加粗部分总长度)为 ;两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图11-2所示,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线l.则 .
三、解答题
19.已知一个正多边形相邻的内角比外角大.
(1)求这个正多边形的内角与外角的度数;
(2)求这个正多边形的边数.
20.如图,五边形的内角都相等,各边也都相等,是它的一个外角,求的度数.
21.如图,为正五边形.
(1)求的度数;
(2)连接,求证:.
22.如图,用n个全等的正五边形按如图方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形.
(1)求的度数;
(2)求的度数;
(3)求n的值.
23.如图,在平面直角坐标系中,,,, .
(1)求证:;
(2)求证:;
(3)求四边形的面积.
24.和分别是两个多边形,阅读和的对话,完成下列各小题.
(1)嘉嘉说:“因为的边数比多,所以的外角和比的大,”判断嘉嘉的说法是否正确?并说明理由;
(2)设的边数为
①若,求的值;
②淇淇说:“无论取何值,的值始终不变.”请用列方程的方法说明理由.
25.探究归纳题:
(1)如图1,经过四边形的一个顶点可以作 条对角线,它把四边形分成 个三角形;
(2)如图2,经过五边形的一个顶点可以作 条对角线,它把五边形分成 个三角形;
(3)探索归纳:对于边形,过一个顶点可以作 条对角线,它把边形分成 个三角形;(用含的式子表示)
(4)如果经过多边形的一个顶点可以作100条对角线,那么这个多边形的边数为 .
答案
一、单选题
1.C
【分析】根据多边形的定义判断即可.
【解析】由一些线段首尾顺次相接组成的封闭图形叫做多边形,①不正确;易知②③正确,
故选:C.
2.C
【分析】先求出每一个外角的度数,再根据边数=360°÷外角的度数计算即可.
【解析】解:180°-144°=36°,
360°÷36°=10,
∴这个多边形的边数是10.
故选:C.
3.D
【分析】先根据该多边形的内角和是外角和2倍,可得出:(n-2) 180=360×2,求出多边形的边数n,再根据n边形对角线的总条数为:,求解即可.
【解析】设这个多边形有n条边,由题意得:
(n 2)×180=360×2,
解得:n=6,
从这个多边形的对角线的条数是=9,故D正确.
故选:D.
4.C
【分析】设这个外角是x°,则内角是3x°,根据内角与它相邻的外角互补列出方程求出外角的度数,根据多边形的外角和是360°即可求解.
【解析】解:∵一个正多边形每个内角与它相邻外角的度数比为3:1,
∴设这个外角是x°,则内角是3x°,
根据题意得:x+3x=180°,
解得:x=45°,
360°÷45°=8(边),
故选:C.
5.C
【分析】先根据多边形的外角和求多边形的边数,再根据多边形的内角和公式求出即可.
【解析】解:设这个多边形是n边形,根据多边形的外角和为360°可得,40°×n=360°,
解得n=9.
所以这个多边形的内角和为(9-2)×180°=1260°.
故选C.
6.D
【分析】正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
【解析】解:A.正六边形的每个内角是120°,正五边形每个内角是180°-360°÷5=108°,120m+108n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
B.正八边形的每个内角为:180°-360°÷8=135°,正三角形的每个内角60°.135m+60n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
C.正五边形每个内角是180°-360°÷5=108°,正八边形的每个内角为:180°-360°÷8=135°,108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
D.正六边形的每个内角是180°-360°÷6=120°,正三角形的每个内角是60°,2×120°+2×60°=360°,或120°+4×60°=360度,能铺满;
故选:D.
7.A
【分析】设多边形的边数是n,没加的内角为x,根据多边形的内角和公式,进行计算即可得解.
【解析】解:设多边形的边数是n,没加的内角为x,
根据题意得:,
∵,
∴,.
故选:A.
8.A
【分析】根据多边形的内角和求出剪去一个角后的多边形的边数即可判断.
【解析】解:由题意得,
,解得,
由于剪去一个角后边数为6,则这个多边形不可能为四边形,
故选A.
9.C
【分析】根据题意可得从n边型的同一个顶点出发,可以引条对角线.
【解析】解:∵从一个四边形的同一个顶点出发可以引出条对角线;
从五边形的同一个顶点出发,可以引出条对角线,
从六边形的同一个顶点出发,可以引出条对角线,
∴从n边型的同一个顶点出发,可以引条对角线,
故选:C.
10.C
【分析】本题只看图觉得很复杂,但从数据入手,就简单了,从图2开始,每个图都比前一个图多360度.抓住这点就很容易解决问题了.
【解析】解:依题意可知,二环三角形,S=360度;
二环四边形,S=720=360×2=360×(4﹣2)度;
二环五边形,S=1080=360×3=360×(5﹣2)度;
…
∴二环十边形,S=360×(10﹣2)=2880度.
故选:C.
二、填空题
11. 不在同一条直线上的n()条线段首尾顺次连接组成的 多边形的边 顶点 n边形 相邻两边组成的角 延长线 不相邻两个顶点
【分析】利用多边形定义、多边形内角、多边形外角及多边形对角线定义填空即可.
【解析】在同一平面内,由不在同一条直线上的n()条线段首尾顺次连接组成的图形叫多边形.
组成多边形的线段叫做多边形的边,
相邻两边的公共端点叫多边形的顶点.
如果一个多边形有n条边,那么这个多边形叫做n边形.
多边形相邻两边组成的角叫做它的内角,
多边形的边与它邻边延长线组成的角叫多边形的外角.
连接多边形不相邻两个顶点的线段叫做多边形的对角线.
故答案为:不在同一条直线上的n()条线段首尾顺次连接组成的;多边形的边;顶点;n边形;相邻两边组成的角;延长线;不相邻两个顶点.
12.十二
【解析】设此多边形有n条边,
根据题意得:(n-2)·180°=5×360°,
解得n=12.
故答案为12.
13. 180° 不变
【分析】多边形的内角和定理:n边形的内角和是(n-2)·180°(n≥3,且n为正数);所以当边数加1,内角和增加180°,任何多边形的外角和都是360°.
【解析】根据多边形的内角和定理,多边形的边数每增加1,它的内角和就增加180°;
任何多边形的外角和都是360°,所以外角和不变.
故答案为180°;不变.
14.5或6或7
【分析】本题考查多边形内角和定理、剪纸问题,掌握多边形的内角和定理及分类讨论问题是解题的关键.设剪去一个角后的多边形边数为n,利用多边形内角和公式则有,解出方程就可以得到新多边形的边数;然后通过分析当沿的是对角线和沿的不是对角线这两种方式剪角,就可以求出原来多边形的边数.
【解析】解:设内角和为的多边形的边数为n,则,
解得,
即得到的多边形是6边形,
当沿的是一条对角线剪去一个角,则原来的是7边形,
当沿的直线并不是对角线时,分为两种情况:
①过多边形的一个顶点,则原来的是6边形;
②不过多边形的顶点,则原来的是5边形,
综上所述,原多边形的边数为5或6或7,
故答案为:5或6或7.
15.
【分析】分两种情况分别画出图形,根据直角三角形各角的度数和四边形内角和进行求解,最后通过比较即可得出最大角的度数.本题主要考查了四边形的内角和,分类讨论和正确画出图形是解题的关键.
【解析】解:如图1所示,在中,,, 于点D,则,
∴,
如图2所示,在中,,, 于点D,则,
∴,
∵,
∴在四边形中,最大角的度数是.
故答案为:
16.
【分析】利用多边形的外角和定理,即减去等边三角形的一个内角的度数,减去正五边形的一个内角的度数,减去正方形的一个内角的度数,再减去和的度数,最后得出答案.
【解析】等边三角形的内角的度数是,正方形的内角的度数为,正五边形的内角的度数是,
则.
故答案为:
17.40.
【分析】在DO延长线上找一点M,根据多边形的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【解析】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∴∠BOM=360°﹣220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°﹣∠BOM=180°﹣140°=40°.
故答案为:40
18.
【分析】题考查正六边形的特征,解题的关键是掌握正六边形的每个外角都是.
(1)运用组成图形的边的数量和乘以边长解题即可;
(2)根据六边形的外角和平行线的性质解题即可.
【解析】解:图1中螺母组成的图形的周长为:;
如图,延长交直线l于点C,延长交于点F,
∵直线l,
∴,
又∵,
∴,即,
又∵图形是正六边形,
∴,
∴,
故答案为:;.
三、解答题
19.(1)设正多边形的外角为,则内角为,由题意,得
,
解得.
正多边形的内角为,外角为.
(2)这个正多边形的边数为:.
20.解:∵五边形的内角都相等,
∴五边形的外角都相等,
∴,
∴五边形的每个内角度数为:,
∵,
∴,
∴.
21.(1)解:∵正五边形的每一个内角的度数为:,
∴;
(2)解:∵五边形是正五边形,
∴,,
∴在和中,
,
∴,
∴.
22.(1)解:正五边形内角和为,
故;
(2)解:∵,
∴;
(3)解:由题意得:,
解得:.
23.(1)解:如图:在四边形中,
,
,
,
,
,
,
又,
.
(2)解:如图2,过点A作于点,作的延长线于点E,
,,,
,,
,
又,
,
又∵AF⊥BC,,
,,
,
,
.
(3)解:如图2:作轴于点.
,,,
.
,.
.
24.(1)解:嘉嘉的说法不正确;
理由:多边形的外角和始终为,与多边形的边数无关;
(2)①,
解得,
即的值为;
②,
整理得,
解得.
∴无论取何值,的值始终不变.
25.(1)如图1:
经过1个顶点做1条对角线,它把四边形分为2个三角形,
故答案为:1,2
(2)如图2:
经过五边形一个顶点,共有2条对角线,将这个多边形分为3个三角形;
故答案为:2,3.
(3)∵经过四边形的一个顶点可以作条对角线,它把四边形分成个三角形;
经过五边形的一个顶点可以作条对角线,它把五边形分成个三角形;
经过六边形的一个顶点可以作条对角线,它把六边形分成个三角形;
经过七边形的一个顶点可以作条对角线,它把七边形分成个三角形;
……
∴经过n边形的一个顶点可以作条对角线,它把n边形分成个三角形;
故答案为:,.
(4)∵过多边形的一个顶点可以作100条对角线,
∴根据(3)中结论可得,,
∴,
故答案为:103.
