沪教版(五四学制)八年级数学下册 22.3 特殊的平行四边形 练习(含详解)
文档属性
| 名称 | 沪教版(五四学制)八年级数学下册 22.3 特殊的平行四边形 练习(含详解) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-13 00:00:00 | ||
图片预览

文档简介
22.3 特殊的平行四边形
一、单选题
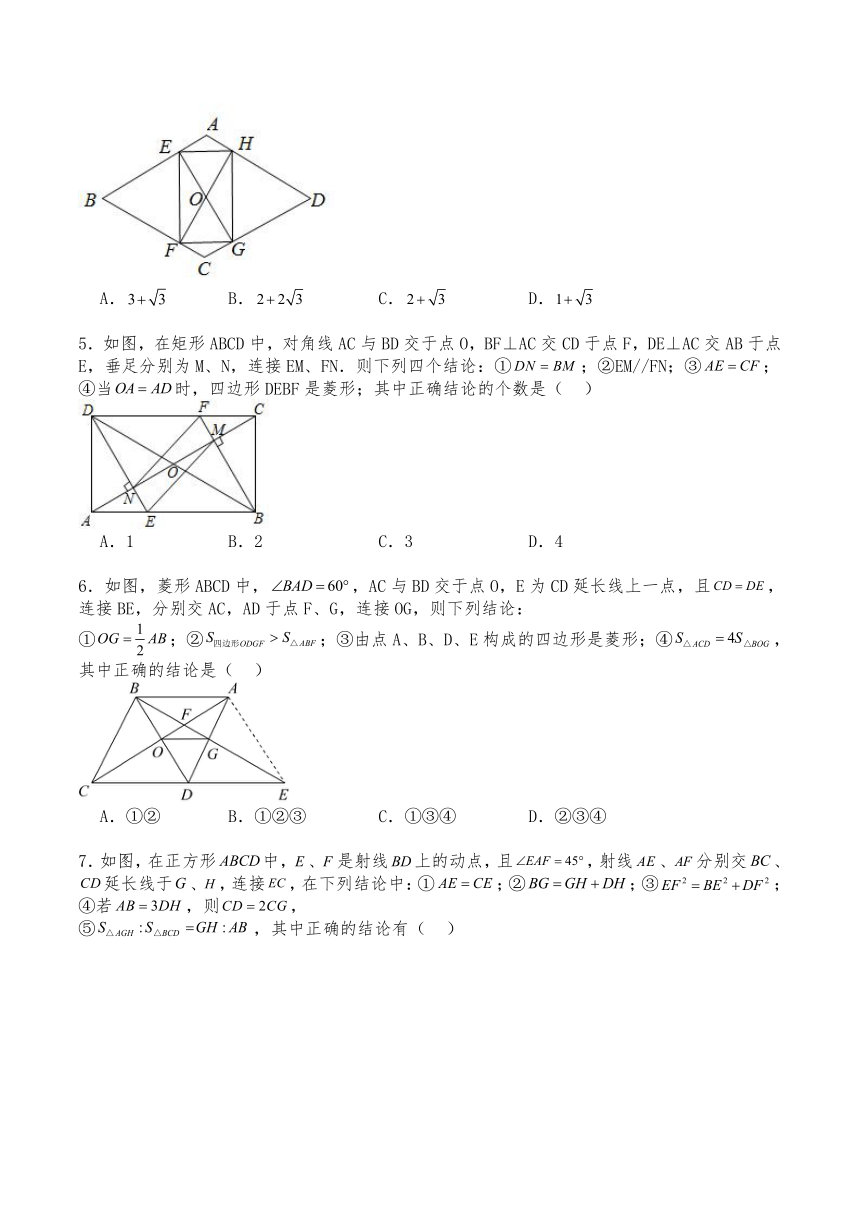
1.如图,E、F、H分别为正方形的边、、上的点,连接,,且,平分交于点G.若,则的度数为( )
A.26° B.38° C.52° D.64°
2.如图:是边长为1的正方形的对角线上一点,且,为上任意一点,于点,于点,则的值是( )
A. B. C. D.
3.如图,在长方形中,,对角线,平分交于点,是线段上的点,连接,过点作交的延长线于点,当为等腰三角形时,( )
A.4 B.5 C.6 D.7
4.如下图,在菱形中,,,过菱形的对称中心分别作边,的垂线,交各边于点,,,,则四边形的周长为( )
A. B. C. D.
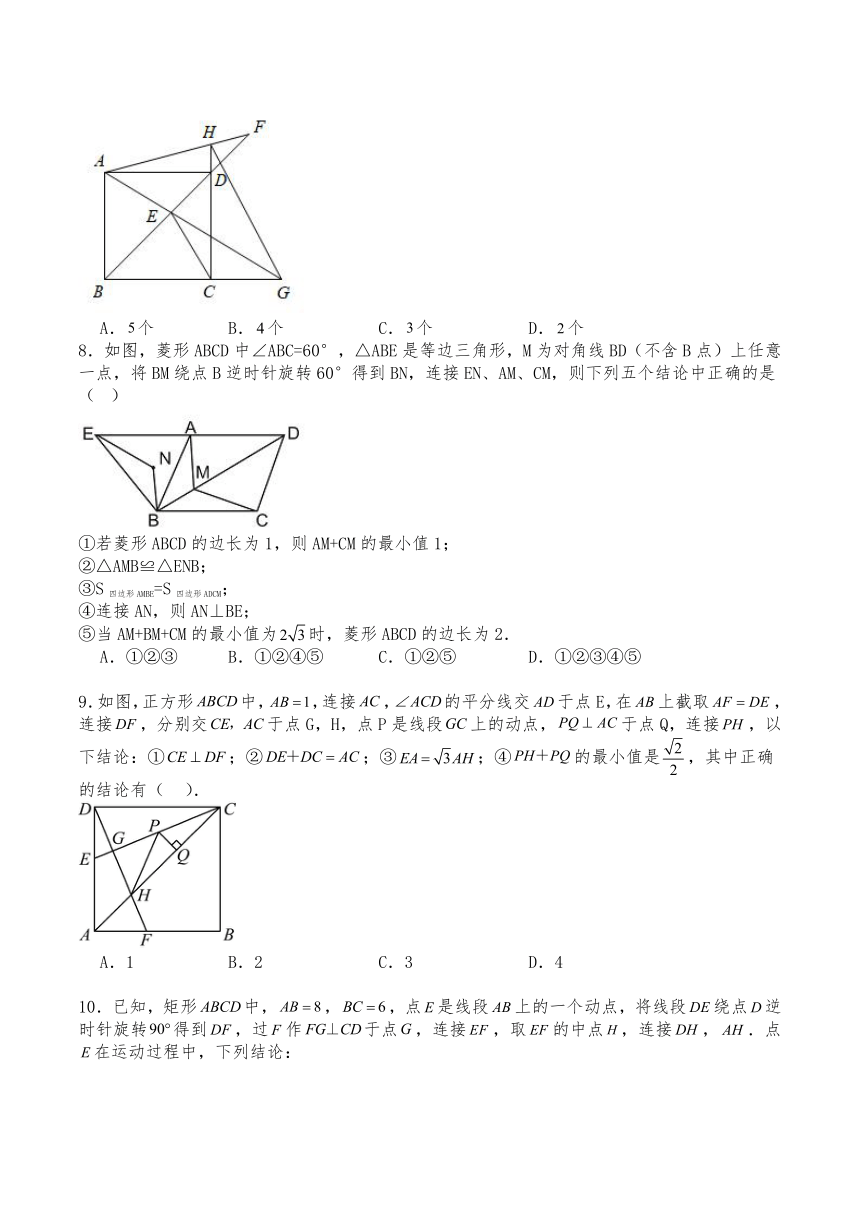
5.如图,在矩形ABCD中,对角线AC与BD交于点O,BF⊥AC交CD于点F,DE⊥AC交AB于点E,垂足分别为M、N,连接EM、FN.则下列四个结论:①;②EM//FN;③;④当时,四边形DEBF是菱形;其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.如图,菱形ABCD中,,AC与BD交于点O,E为CD延长线上一点,且,连接BE,分别交AC,AD于点F、G,连接OG,则下列结论:
①;②;③由点A、B、D、E构成的四边形是菱形;④,其中正确的结论是( )
A.①② B.①②③ C.①③④ D.②③④
7.如图,在正方形中,、是射线上的动点,且,射线、分别交、延长线于、,连接,在下列结论中:①;②;③;④若,则,
⑤,其中正确的结论有( )
A.个 B.个 C.个 D.个
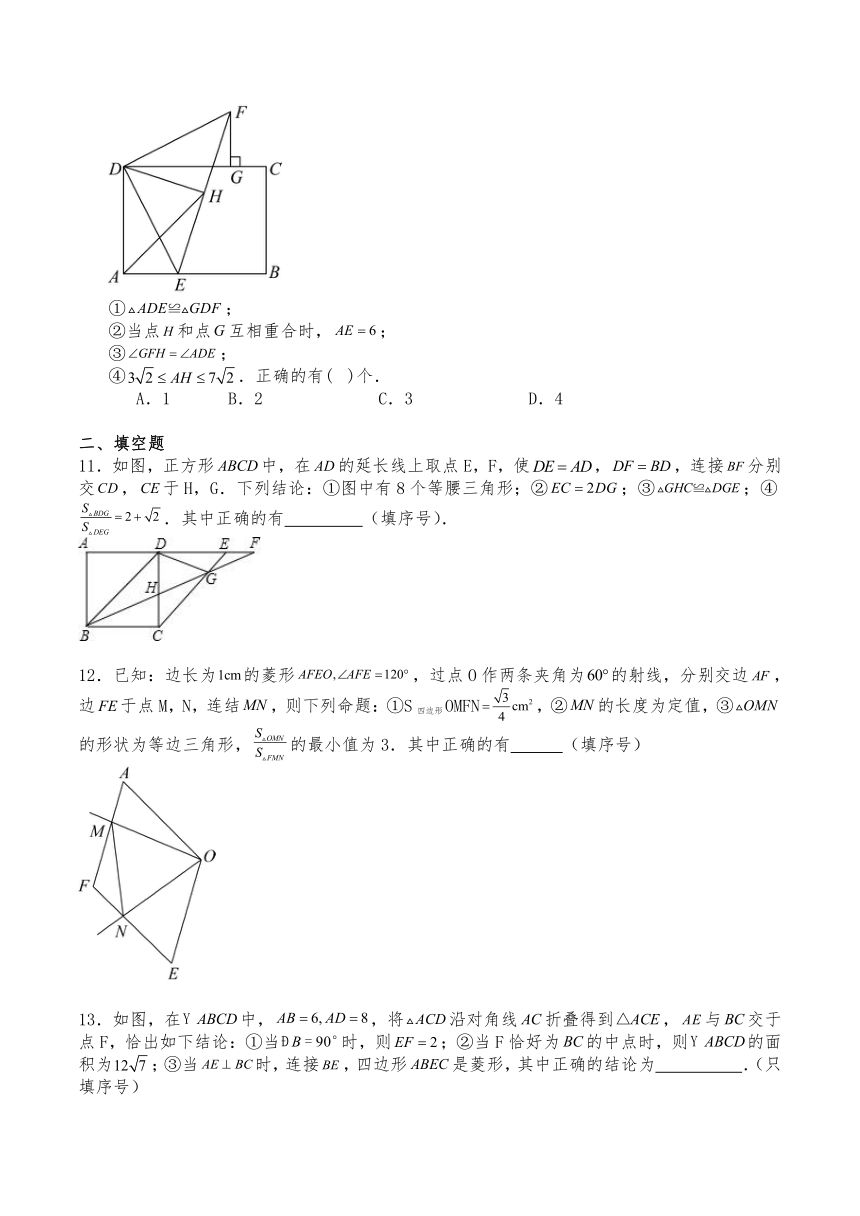
8.如图,菱形ABCD中∠ABC=60°,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为时,菱形ABCD的边长为2.
A.①②③ B.①②④⑤ C.①②⑤ D.①②③④⑤
9.如图,正方形中,,连接,的平分线交于点E,在上截取,连接,分别交于点G,H,点P是线段上的动点,于点Q,连接,以下结论:①;②;③;④的最小值是,其中正确的结论有( ).
A.1 B.2 C.3 D.4
10.已知,矩形中,,,点是线段上的一个动点,将线段绕点逆时针旋转得到,过作于点,连接,取的中点,连接,.点在运动过程中,下列结论:
①;
②当点和点互相重合时,;
③;
④.正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.如图,正方形中,在的延长线上取点E,F,使,,连接分别交,于H,G.下列结论:①图中有8个等腰三角形;②;③;④.其中正确的有 (填序号).
12.已知:边长为的菱形,过点O作两条夹角为的射线,分别交边,边于点M,N,连结,则下列命题:①S四边形OMFN,②的长度为定值,③的形状为等边三角形,的最小值为3.其中正确的有 (填序号)
13.如图,在中,,将沿对角线折叠得到,与交于点F,恰出如下结论:①当时,则;②当F恰好为的中点时,则的面积为;③当时,连接,四边形是菱形,其中正确的结论为 .(只填序号)
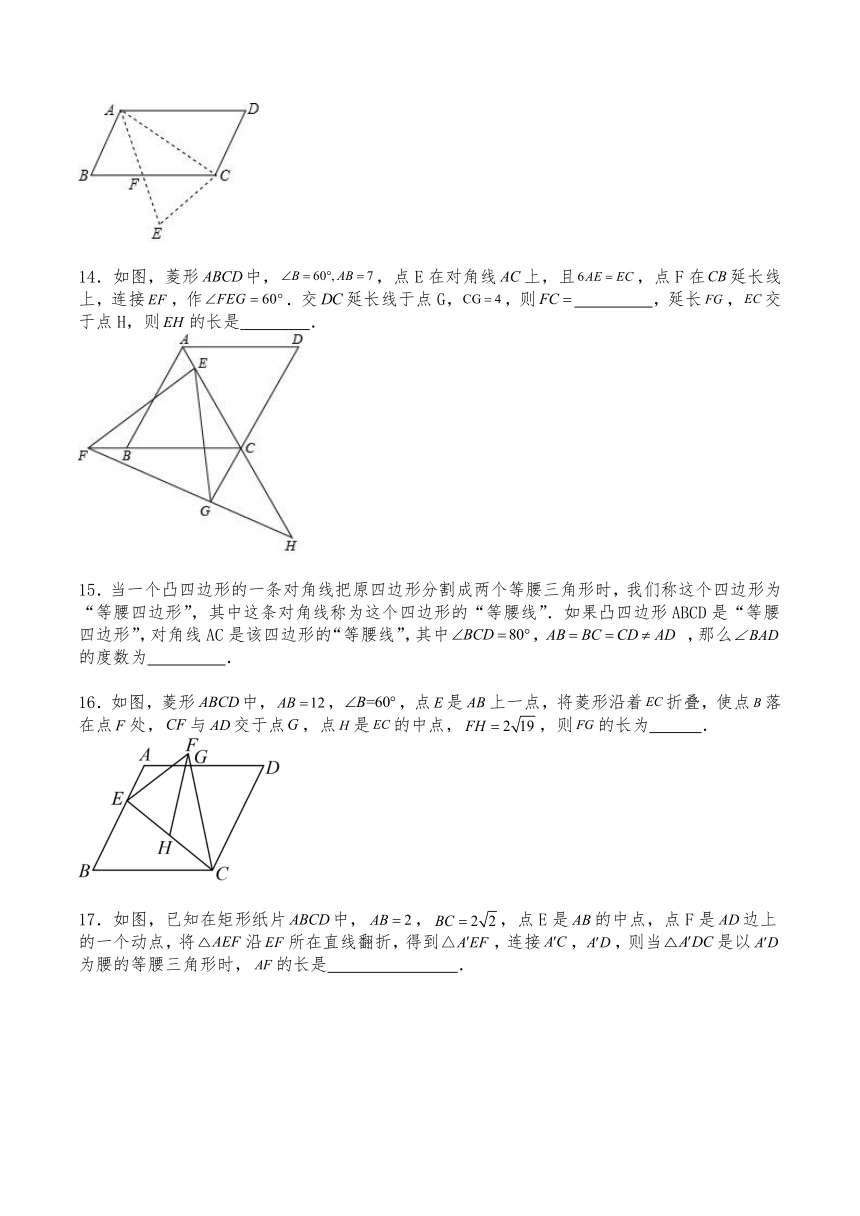
14.如图,菱形中,,点E在对角线上,且,点F在延长线上,连接,作.交延长线于点G,,则 ,延长,交于点H,则的长是 .
15.当一个凸四边形的一条对角线把原四边形分割成两个等腰三角形时,我们称这个四边形为“等腰四边形”,其中这条对角线称为这个四边形的“等腰线”.如果凸四边形ABCD是“等腰四边形”,对角线AC是该四边形的“等腰线”,其中, ,那么的度数为 .
16.如图,菱形中,,,点是上一点,将菱形沿着折叠,使点落在点处,与交于点,点是的中点,,则的长为 .
17.如图,已知在矩形纸片中,,,点E是的中点,点F是边上的一个动点,将沿所在直线翻折,得到,连接,,则当是以为腰的等腰三角形时,的长是 .
18.如图,矩形中,,点H在边上,,E为边上一个动点,连.以为一边在的右上方作菱形,使点G落在边上,连结.
(1)当菱形为正方形时,的长为 ;
(2)在点E的运动过程中,的面积S的取值范围为 .
三、解答题
19.四边形中,对角线于点,且;
(1)如图1,若,求四边形的面积;
(2)如图2,若,,求;
(3)如图3,若,,,求四边形的面积.
20.在正方形ABCD中,AB=4,点E是边AD上一动点,以CE为边,在CE的右侧作正方形CEFG,连结BF.
(1)如图1,当点E与点A重合时,则BF的长为 .
(2)如图2,当AE=1时,求点F到AD的距离和BF的长.
(3)当BF最短时,请直接写出此时AE的长.
21.在平行四边形ABCD中,,连接,已知,点在线段上,将线段绕点顺时针旋转为线段.
(1)如图1,线段与线段的交点和点重合,连接,求线段的长度;
(2)如图2,点为延长线上一点,连接交于点,连接EG,若点H为线段的中点,求证:;
(3)如图3,在(2)的条件下,连接,延长交于点,连接,直接写出线段长度的最小值.
22.如图1,在矩形中,,,点为边上一动点,连结,作点关于直线的对称点,连结,,,,与交于点.
(1)若,求证:.
(2)如图2,连结,,若点在矩形的对角线上,求所有满足条件的的长.
(3)如图3,连结,当点到矩形一个顶点的距离等于2时,请直接写出的面积.
23.在正方形中,点是边上点,点在的延长线上,将线段绕点顺时针旋转,到线段,连接.
(1)如图,连接,判断线段与线段的数量关系给出证明.
(2)如图,若正好经过点.
①直接用等式表示线段、和的数量关系为______.
②证明:.
(3)如图,当经过点时,若,,请直接写出此时正方形边的长度.
24.如图1,四边形为菱形,.,,.
(1)点A坐标为 ,四边形的面积为 ;
(2)如图2,点E在线段上运动,为等边三角形.
①求证:,并求的最小值;
②点E在线段上运动时,点F的横坐标是否发生变化?若不变,请求出点F的横坐标.若变化,请说明理由.
25.在矩形中,,,E、F是直线上的两个动点,分别从A、C两点同时出发相向而行,速度均为每秒2个单位长度,运动时间为t秒,其中.
(1)如图1,M、N分别是中点,当四边形是矩形时,求t的值;
(2)若G、H分别从点A、C沿折线,运动,与相同的速度同时出发.
①如图2,若四边形为菱形,求t的值;
②如图3,作的垂直平分线交于点P、Q,当四边形的面积是矩形面积的时,则t的值是______.
答案
一、单选题
1.D
【分析】过点作,由正方形的性质,,,四边形为矩形,利用HL易证得,可得,进而可得,由角平分线可得的度数,即可求得得度数.
【解析】解:过点作,
∵四边形是正方形,
∴,,
∵,则四边形为矩形,
∴,
∵,
∴(HL),
∴,
∵,
∴,
又∵平分,
∴,
∴.
故选:D.
2.C
【分析】连接,过作,利用面积法求解,的值等于点到的距离,即正方形对角线的一半.
【解析】解:连接,过作,如图所示:
,
,
,
四边形是正方形,
,,,
,
,,
为中点,
,
即值是.
故选:C.
3.B
【分析】过作于,由矩形的性质并结合勾股定理确定,再证明以及为等腰三角形,即可推导,,然后由计算的长即可.
【解析】解:过作于,
∵四边形是矩形,
∴,,,
∵,
∴,
∵,,
∴,
∴,
∴,
∵平分交于点,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∵为等腰三角形,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
故选:B.
4.A
【分析】先证明是等边三角形,求出EF,同理可证都是等边三角形,然后求出EH,GF,FG即可.
【解析】解:如图,连接BD,AC,
∵四边形ABCD是菱形,,
∴,,
∴,
∴,
∵,
∴,
在中,,,
∵在和 BFO中,
,
∴,
∴,
∵,
∴是等边三角形,
∴,
同法可证,都是等边三角形,
∴,,
∴四边形EFGH的周长为.
故选:A.
5.D
【分析】根据矩形的性质得到AB=CD,AB//CD,∠DAE=∠BCF=90°,OD=OB=OA=OC,AD=BC,AD//BC,根据平行线的性质得到DE⊥AC,根据垂直的定义得到∠DNA=∠BMC=90°,由全等三角形的性质得到DN=BM,∠ADE=∠CBF,故①正确;证△ADE≌△CBF(ASA),得出AE=FC,DE=BF,故③正确;证四边形NEMF是平行四边形,得出EM//FN,故②正确;证四边形DEBF是平行四边形,证出∠ODN=∠ABD,则DE=BE,得出四边形DEBF是菱形;故④正确;即可得出结论.
【解析】解:∵四边形ABCD是矩形,
∴AB=CD,AB//CD,∠DAE=∠BCF=90°,OD=OB=OA=OC,AD=BC,AD//BC,
∴∠DAN=∠BCM,
∵BF⊥AC,DE//BF,
∴DE⊥AC,
∴∠DNA=∠BMC=90°,
在△DNA和△BMC中,
,
∴△DNA≌△BMC(AAS),
∴DN=BM,∠ADE=∠CBF,故①正确;
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=FC,DE=BF,故③正确;
∴DE -DN=BFBM,即NE=MF,
∵DE//BF,
∴四边形NEMF是平行四边形,
∴EM//FN,故②正确;
∵AB=CD,AE=CF,
∴BE=DF,
∵BE//DF,
∴四边形DEBF是平行四边形,
∵AO=AD,
∴AO=AD=OD,
∴△AOD是等边三角形,
∴∠ADO=∠DAN=60°,
∴∠ABD=90°-∠ADO=30°,
∵DE⊥AC,
∴∠ADN=∠ODN=30°,
∴∠ODN=∠ABD,
∴DE=BE,
∴四边形DEBF是菱形;故④正确;
故选:D.
6.C
【分析】①由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ABD的中位线,得出OG=AB,①正确;
③先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;
②连接FD,由等边三角形的性质和角平分线的性质得F到△ABD三边的距离相等,则S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF,则S四边形ODGF=S△ABF,②错误;即可得出结论.
④∵连接CG,由O、G分别是AC,AD的中点,得到,则S△ACD=4S△AOG,再由S△AOG=S△BOG,得到S△ACD=4S△BOG,故④正确;
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ABD的中位线,
∴OG=AB,故①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴平行四边形ABDE是菱形,故③正确;
∵连接CG,
∵O、G分别是AC,AD的中点,
∴,
∴S△ACD=4S△AOG,
∵,
∴S△AOG=S△BOG,
∴S△ACD=4S△BOG,故④正确;
连接FD,如图:
∵△ABD是等边三角形,AO平分∠BAD,BG平分∠ABD,
∴F到△ABD三边的距离相等,
∴S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF,
∴S四边形ODGF=S△ABF,故②错误;
正确的是①③④,
故选C.
7.B
【分析】由“”可证,可得,故正确;
如图,在上截取连接,由“”可证,可得,由“”可证,可得,
,故正确;
如图2,将绕点顺时针旋转,得到,连接,由旋转的性质可得,,,由“”可证,可得,由勾股定理可得,故正确;
如图1,设,则,利用勾股定理可求,故错误;
由三角形的面积公式可求,故正确;
【解析】解:四边形是正方形,
,,
,
,
,
故正确;
如图1,在上截取,连接,
,,,
,
,,
,
,
,
又,,
,
,,
故正确;
如图2,将绕点顺时针旋转,得到,连接,
,,
,,,
∵∠ABD=∠ADB=450,
,,
,
,
又,,
,
,
在中, ,
,
故正确;
,
设,则,
,
如图1,在上截取,连接,
由可得:,
设,则,
,
,
,
,
,
故错误;
如图1,,
,
,
故正确;
正确的结论有,共个.
故选:
8.C
【解析】试题分析:①连接AC,交BD于点O,∵四边形ABCD是菱形,∴AB=BC,BD⊥AC,AO=BO,∴点A,点C关于直线BD对称,∴M点与O点重合时AM+CM的值最小为AC的值,∵∠ABC=60,∴△ABC是等边三角形,∴AB=AC,∵AB=1,∴AC=1,即AM+CM的值最小为1,故本答案正确;
②∵△ABE是等边三角形,∴BA=BE,∠ABE=60°,∵∠MBN=60°,∴∠MBN﹣∠ABN=∠ABE﹣∠ABN,即∠MBA=∠NBE,又∵MB=NB,∴△AMB≌△ENB(SAS),故本答案正确;
③∵S△ABE+S△ABM=S四边形AMBE,S△ACD+S△AMC=S四边形ADCM,且S△AMB≠S△AMC,∴S△ABE+S△ABM≠S△ACD+S△AMC,∴S四边形AMBE≠S四边形ADCM,故本答案错误;
④假设AN⊥BE,且AE=AB,∴AN是BE的垂直平分线,∴EN=BN=BM=MA,∴M点与O点重合,∵条件没有确定M点与O点重合,故本答案错误;
⑤如图,连接MN,由(1)知,△AMB≌△ENB,∴AM=EN,∵∠MBN=60°,MB=NB,∴△BMN是等边三角形,∴BM=MN,∴AM+BM+CM=EN+MN+CM,根据“两点之间线段最短”,得EN+MN+CM=EC最短,∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.过E点作EF⊥BC交CB的延长线于F,∴∠EBF=180°﹣120°=60°,设菱形的边长为x,∴BF=,EF=,在Rt△EFC中,∵,∴,解得x=2,故本答案正确.
综上所述,正确的答案是:①②⑤,故选C.
9.C
【分析】本题综合考查了正方形的性质,全等三角形的性质,能够合理选择正方形的性质找到全等三角形是解题的关键.
①利用正方形的性质证明得到进而可证;②利用正方形的性质证明,得到,证明,进而可证;③求得的长度,然后求出,进而可证;④证明垂直平分,过点作,利用垂线段最短可知的长度为最小值,利用等面积法可求.
【解析】∵正方形,
∴, ,
∴,
在和中,
,
∴,
∴,
,
∴,
∴,故①正确;
∵平分,
∴,
在和中,
,
∴,
∴,
∵正方形,
∴,
∴,
∴,
∵,
∴,
∴,
∴,故②正确;
∵,
∴
,
,
,
即,结论③错误;
,
,
,
∴垂直平分,
,
当时,有最小值,
过点作,
则的长度为的最小值,
,
即的最小值为,故④正确.
正确的为: ①②④,个数为3
故选:C
10.C
【分析】由四边形是矩形,线段绕点逆时针旋转得到,可证,故①正确;当点和点互相重合时,由是等腰直角三角形,是的中点,,可得∠AED=450 =∠ADE,从而,故②正确;由等腰直角三角形的三线合一和得,从而得到,故③错误;分别求出的最大值、最小值,可得,故④正确.
【解析】解:四边形是矩形,
,
线段绕点逆时针旋转得到,
,∠AED=450 =∠ADE,
,
,
,
,故①正确;
当点和点互相重合时,如图,
线段绕点逆时针旋转得到,
,,
是等腰直角三角形,
是的中点,,
,
,
,
,故②正确;
线段绕点逆时针旋转得到,
,
是的中点,,
,
,故③错误;
当与重合时,最短,如图:
,
此时与都在上,
是等腰直角三角形,是的中点,
是等腰直角三角形,
,
,
,
的最小值为,
当与重合时,最大,过作于,如图:
,
,
,
,,,
,
设,则,
,
,
解得:(舍去)或,
,
,
,
的最大值为,
,故④正确;
综上所述,正确的有①②④,共3个,
故选:C.
二、填空题
11.③④
【分析】①根据正方形的性质及等腰三角形的判定,可得出图中共有9个等腰三角形;②根据正方形的性质和已知推出四边形DECB是平行四边形,得到BD=CE,BD∥CE,无法证出G为CE的中点;③由SAS可证明△GHC≌△DGE;④由上述推理可得,△DBG∽△GDE,再根据三角形的面积等于相似比的平方可得结论.
【解析】解:如图,在正方形中,
,,
和是等腰三角形;
,,
和是等腰三角形;
,,
,
,
∵ BCG和是等腰三角形;
,,
是等腰三角形,且,,
,,
∵ DHG和是等腰三角形,
综上,图中共有9个等腰三角形;故①不正确;
正方形,,
,,,
四边形是平行四边形,
,,
,
,
要使,只要为的中点即可,
且,,
,
即和不全等,
点不是中点,②错误
由①分析可知,
在和中,
,
;故③正确;
如图,过点作交的延长线于点,交AF于N,
设NG=x,则MG=1-x,
∵△CDE为等腰三角形,
∴∠DCE=∠DEC=45°,
可得△CGM为等腰直角三角形,
∴CM=1-x,
∴CG=,
设正方形ABCD的边长为1,
则BC=DE=1,BD=DF=CE=,
∵△BCG为等腰三角形,
∴,
解得:,
∴,故④正确;
综上,③④正确.
故答案为:③④.
12.①③
【分析】连接,由菱形的性质得出,,,,得出是等边三角形,得出,,证明得出,证出是等边三角形,得出②不正确, 的面积的面积,得出的面积,①正确,当时,最小,等边的面积最小,求出的面积,得出,③正确;即可得出结论.
【解析】解:连接,如图所示:
四边形是菱形,
,,,,
是等边三角形,
,,
,
,
在和中,
,
,
,
是等边三角形,②不正确, 的面积的面积,
的面积,①正确,
当时,最小,等边的面积最小,
的面积,
,③正确;
故答案为:①③.
13.②
【分析】①设AF=CF=x,构建方程求出x即可判断;②证明∠BAC=90°,利用勾股定理求出AC,求出平行四边形ABCD的面积即可判断;③当AE⊥BC时,四边形ABEC是等腰梯形,不符合题意.
【解析】解:①如图1中,
∵∠B=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠DAC=∠CAE,
∴∠ACF=∠CAF,
∴AF=CF,设AF=CF=x,
在Rt△ABF中,则有x2=62+(8-x)2,
解得x=,
∴EF=8-=,故错误;
如图2中,
当BF=CF时,
∵AF=CF=BF,
∴∠BAC=90°,
∴AC=,
∴S平行四边形ABCD=AB AC=6×=,故正确;
如图3中,
当AE⊥BC时,四边形ABEC是等腰梯形,故错误.
故答案为:②.
14.
【分析】先根据题意求得,如图,过点作,则可的是等边三角形,由可得,,则,,进而根据AAS可证明,进而可得的长,过点作于点,过作于,根据勾股定理可得的长,设,进而求得的长由,可得是等边三角形,进而求得,根据的面积等于,据此列出方程,解方程即可求得,进而求得.
【解析】如图,过点作,
四边形是菱形,
,是等边三角形
是等边三角形
,
,
即
在和中
(AAS)
,
是等边三角形,
过点作于点,过作于,如图,
在中,
在中,
在中,设,
是等边三角形,
的面积等于
整理得
因式分解得:
解得或(舍)
故答案为:
15.
【分析】根据“等腰四边形”的定义画出图形,对角线是该四边形的“等腰线”,所以和为等腰三角形,由于,中分两种情形:①,②.当时,由于,可得为等边三角形,,则,结论可得;当时,过点作,根据等腰三角形的三线合一,,过点作,交延长线于点,根据四边形为矩形,,可得,由于,可得,从而可求.
【解析】解:凸四边形是“等腰四边形”,对角线是该四边形的“等腰线”,
和为等腰三角形.
由于,在中分两种情形:①,②.
当①时,如下图:
,.
.
为等边三角形.
.
,
.
,
.
当②时,如下图,
过点作,过点作,交延长线于点,
,,
.
,,,
四边形为矩形.
.
,
.
在中,,
.
,
.
,
.
,
.
综上,.
故答案为:.
16.
【分析】连接,过点作的平行线交于点,过点作交延长线于点,延长交于点,过点作于点,利用翻折的性质和勾股定理求出,然后证明,得,证明,再利用勾股定理求出,进而即可解决问题.
【解析】解:如图,连接,过点作的平行线交于点,过点作交延长线于点,延长交于点,过点C作于点,
由翻折可知:,
∵点是的中点,,为菱形,
∴,
设,
在中,,
由勾股定理得:,
整理得,
解得(舍去负值),
∵HI∥BC∥AD,
∵∠AEK=∠HEI,
由翻折可知:,
∵BC∥AD,
设
∵CL⊥AD,∠D=600 ,CD=12 ,
在中,由勾股定理得:
故答案为:.
17.1或
【分析】存在三种情况:当时,连接ED,利用勾股定理可以求得ED的长,可判断三点共线,根据勾股定理即可求解;当时,可以证得四边形是正方形,即可求解;当时,连接EC,FC,证明三点共线,再用勾股定理,即可求解.
【解析】解:①当时,连接ED,如图,
∵点E是的中点,,,四边形是矩形,
∴,
由勾股定理可得,,
∵将沿所在直线翻折,得到,
∴,
∵,
∴,
∴三点共线,
∵,
∴,
设,则,,
在中,,
∴,
解得,
∴;
②当时,如图,
∵,
∴点在线段CD的垂直平分线上,
∴点在线段AB的垂直平分线上,
∵点E是的中点,
∴是AB的垂直平分线,
∴,
∵将沿所在直线翻折,得到,
∴,
∴四边形是正方形,
∴;
综上所述,AF的长为1或.
故答案为:1或.
18. 1
【分析】(1)由于四边形ABCD为矩形,四边形HEFG为正方形,那么∠D=∠A=∠GHE=90°,HG=HE,易证△GDH≌△HAE,得DG=AH=1;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=1,进而可求△FCG的面积S的最大值和最小值,从而确定S的取值范围.
【解析】解:(1)如图1,当菱形为正方形时,,,
四边形为矩形,
,
,
,
在和中,
,
,
;
故答案为:1;
(2)如图2,过作,交延长线于,连接,
,
,
,
,
,
在和中,
,
,即无论菱形如何变化,点到直线的距离始终为定值1,
因此,
设,则,
在中,,
,
,
,
,
的最小值为,此时,的最大值为,此时,
在点的运动过程中,的面积的取值范围为:;
故答案为:;
三、解答题
19.解:(1)如图1中,
,,
,
,
.
(2)如图2中,
,
可以假设,,则
,,
,
,,
.
(3)如图3中,过点作于,过点作于.
,
可以假设,,
∵AC⊥BD,
,,,,
,,
,
,
,
,
,
,
,
,
,
,
四边形是矩形,
,,
,
,
整理得,
,
,
经检验:符合题意;
.
20.解:(1)如图,连接DF,
∵∠CAF=90°,∠CAD=45°,
∴∠DAF=45°,
在△CAD和△FAD中,
,
∴△CAD≌△FAD(SAS),
∴DF=CD,
∴∠ADC=∠ADF=90°,
∴C,D,F共线,
∴BF2=BC2+CF2=42+82=80,
∴BF=,
故答案为:;
(2)如图,过点F作FH⊥AD交AD的延长线于点H,FH⊥BC交BC的延长线于K,
∵四边形CFG是正方形,∴EC=EF,∠FEC=90°,
∴∠DEC+∠FEH=90°,
又∵四边形ABCD是正方形,
∴∠ADC=90°,
∴∠DEC+∠ECD=90°,
∴∠ECD=∠FEH,
又∵∠EDC=∠FHE=90°,
在△ECD和△FEH中,
,
∴△ECD≌△FEH(AAS),
∴FH=ED,
∵AD=4,AE=1,
∴ED=AD -AE=4-1=3,
∴FH=3,即点F到AD的距离为3,
∴∠DHK=∠HDC=∠DCK=90°,
∴四边形CDHK为矩形,
∴HK=CD=4,
∴FK=FH+HK=3+4=7,
∵△ECD≌△FEH,
∴EH=CD=AD=4,
∴AE=DH=CK=1,
∴BK=BC+CK=4+1=5,
在Rt△BFK中,BF=;
(3)∵当A,D,F三点共线时,BF的最短,
∴∠CBF=45°,
∴FH=DH,
由(2)知FH=DE,EH=CD=4,
∴ED=DH=4÷2=2,
∴AE=2.
21.(1)延长,过点作于点,过点作于点,过点作于点,于点,
∴,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∵四边形是平行四边形,
∴,,,,,,
∴,,,
∴是等腰直角三角形,
∴,,
∴,
∵线段绕点顺时针旋转为线段,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,,
∴,
∵,
∴四边形是矩形,
∴,,
∴,
∴.
(2)连接、、,
∵四边形是平行四边形,
∴,,
由(1)得,,,
∴,
∴点、、、四点共圆,
∴,
∴点在的延长线上,
∴,
∴,
∵点为线段的中点,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
∵,,
∴,
∴.
(3)连接,,,,
由(2)得,,点为的中点,,
∴,
∵,,
∴,
∴,
∴,
∵点为的中点,,
∴,
∴,
∵,,
∴,
∵(当且仅当点在线段上时等号成立),
∴,
∴的最小值为.
22.(1)证明:∵点关于的对称点为点,
∴,即点为的中点.
∵,,
∴点为的中点,
∴为的中位线.
∴.
(2)分两种情况:
①如图1,点在对角线上.
∵点关于的对称点为点,
∴,,.
∴AC=5
设,
∴,
∴,即.
②如图2,点在对角线上.
∵,,
∴.
∵S△ABD=
∴.
∴.
设,,
∵DG2+GE2=DE2,
∴
∵S△ADE=
∴
∴.
∴,即.
综上:或.
(3)分三种情况:
①点到矩形顶点A的距离等于2时
∵AF=AD=3>2
∴此种情况不存在;
②当点到矩形顶点的距离等于2时,连接FB,
则BF=2,AF=AD=3
过F作FH⊥AB于H,FQ⊥BC于Q,如图,
∴∠FHB=∠ABC=∠BQF=90°
∴四边形BHFQ是矩形
∴FQ=BH
设BH=x,则AH=4-x
∵FH2=AF2-FH2=FB2-BH2
∴4-x2=9-(4-x)2
∴x=
∴FQ=BH=
∴的面积为=.
③当点到矩形顶点的距离等于2时,如图,连接BF
则FC=2
∵AF+FC≥AC,又AF+FC=5,AC=5
∴AC+FC=AC
∴A,C,F三点共线,F在线段AC上
∵
∴=
即的面积为.
④当点到矩形顶点的距离等于2时,连接BF,过F点作MNAB
则DF=2
∴DG=FG=1
∴AG=
∵
∴MF=
∴NF=MN -MF=4-
∴的面积为=.
综上①当点到矩形顶点的距离等于2时,的面积为;②当点到矩形顶点的距离等于2时,的面积为;③当点到矩形顶点的距离等于2时,的面积为.
23.(1)解:,
证明:四边形是正方形,
,,
将线段绕点顺时针旋转,到线段,
,,
,
≌,
;
(2)解:;
理由如下:如图,连接,
四边形是正方形,
,,
,
,
,
,
;
故答案为:;
证明:,,
,
≌ ADE,
,
,
;
(3)解:如图,连接,过点作于,
,,
,
,,,
,
,
,
,
,
正方形的边长为.
24.(1)解:∵,,,
∴,,
∵四边形为菱形,
∴,,
∴,
∴,
∴,
故答案为:,;
(2)①证明:如图,设交于J.
∵四边形是菱形,
∴,,,
∴,都是等边三角形,
∴,
∴.
∵,
∴,
∴,
∴当时,的值最小.
∵,
∴,
∴
∴AF的最小值为.
②点F的横坐标不变,理由如下:
如图,过点F作于H.
∵,
∴.
∵,
∴,
∴,
∴点F的横坐标为,不变.
25.(1)解:∵四边形是矩形,
∴,,
∴,
∵M、N分别是的中点,
∴,
∵E、F分别从A、C同时出发相向而行,速度均为每秒2个单位长度,
∴,
∴,
∴,,
∴,
∴,
∴四边形是平行四边形,
如图1,连接,
∵四边形是矩形,M,N分别是中点,
∴,,
∴四边形是平行四边形,
∵∠B=900,
∴四边形是矩形,
∵矩形中,,,
∴,,
∵四边形是平行四边形,
∴当时,四边形是矩形,
∴或,
解得:或;
(2)①由(1)知:,
如图2,连接,
∵四边形为菱形,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
②如图3,连接,
由①同理得:,,
由①知:,
∴,
∵G、H分别从点A、C沿折线,运动,
∴,
又∵,
∴,
∴,
同理可证,
∴四边形是平行四边形,
∵四边形的面积是矩形面积的,
∴,
∴,
∴,
∴,
∴,
∴,
∴.
故答案为:.
一、单选题
1.如图,E、F、H分别为正方形的边、、上的点,连接,,且,平分交于点G.若,则的度数为( )
A.26° B.38° C.52° D.64°
2.如图:是边长为1的正方形的对角线上一点,且,为上任意一点,于点,于点,则的值是( )
A. B. C. D.
3.如图,在长方形中,,对角线,平分交于点,是线段上的点,连接,过点作交的延长线于点,当为等腰三角形时,( )
A.4 B.5 C.6 D.7
4.如下图,在菱形中,,,过菱形的对称中心分别作边,的垂线,交各边于点,,,,则四边形的周长为( )
A. B. C. D.
5.如图,在矩形ABCD中,对角线AC与BD交于点O,BF⊥AC交CD于点F,DE⊥AC交AB于点E,垂足分别为M、N,连接EM、FN.则下列四个结论:①;②EM//FN;③;④当时,四边形DEBF是菱形;其中正确结论的个数是( )
A.1 B.2 C.3 D.4
6.如图,菱形ABCD中,,AC与BD交于点O,E为CD延长线上一点,且,连接BE,分别交AC,AD于点F、G,连接OG,则下列结论:
①;②;③由点A、B、D、E构成的四边形是菱形;④,其中正确的结论是( )
A.①② B.①②③ C.①③④ D.②③④
7.如图,在正方形中,、是射线上的动点,且,射线、分别交、延长线于、,连接,在下列结论中:①;②;③;④若,则,
⑤,其中正确的结论有( )
A.个 B.个 C.个 D.个
8.如图,菱形ABCD中∠ABC=60°,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为时,菱形ABCD的边长为2.
A.①②③ B.①②④⑤ C.①②⑤ D.①②③④⑤
9.如图,正方形中,,连接,的平分线交于点E,在上截取,连接,分别交于点G,H,点P是线段上的动点,于点Q,连接,以下结论:①;②;③;④的最小值是,其中正确的结论有( ).
A.1 B.2 C.3 D.4
10.已知,矩形中,,,点是线段上的一个动点,将线段绕点逆时针旋转得到,过作于点,连接,取的中点,连接,.点在运动过程中,下列结论:
①;
②当点和点互相重合时,;
③;
④.正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.如图,正方形中,在的延长线上取点E,F,使,,连接分别交,于H,G.下列结论:①图中有8个等腰三角形;②;③;④.其中正确的有 (填序号).
12.已知:边长为的菱形,过点O作两条夹角为的射线,分别交边,边于点M,N,连结,则下列命题:①S四边形OMFN,②的长度为定值,③的形状为等边三角形,的最小值为3.其中正确的有 (填序号)
13.如图,在中,,将沿对角线折叠得到,与交于点F,恰出如下结论:①当时,则;②当F恰好为的中点时,则的面积为;③当时,连接,四边形是菱形,其中正确的结论为 .(只填序号)
14.如图,菱形中,,点E在对角线上,且,点F在延长线上,连接,作.交延长线于点G,,则 ,延长,交于点H,则的长是 .
15.当一个凸四边形的一条对角线把原四边形分割成两个等腰三角形时,我们称这个四边形为“等腰四边形”,其中这条对角线称为这个四边形的“等腰线”.如果凸四边形ABCD是“等腰四边形”,对角线AC是该四边形的“等腰线”,其中, ,那么的度数为 .
16.如图,菱形中,,,点是上一点,将菱形沿着折叠,使点落在点处,与交于点,点是的中点,,则的长为 .
17.如图,已知在矩形纸片中,,,点E是的中点,点F是边上的一个动点,将沿所在直线翻折,得到,连接,,则当是以为腰的等腰三角形时,的长是 .
18.如图,矩形中,,点H在边上,,E为边上一个动点,连.以为一边在的右上方作菱形,使点G落在边上,连结.
(1)当菱形为正方形时,的长为 ;
(2)在点E的运动过程中,的面积S的取值范围为 .
三、解答题
19.四边形中,对角线于点,且;
(1)如图1,若,求四边形的面积;
(2)如图2,若,,求;
(3)如图3,若,,,求四边形的面积.
20.在正方形ABCD中,AB=4,点E是边AD上一动点,以CE为边,在CE的右侧作正方形CEFG,连结BF.
(1)如图1,当点E与点A重合时,则BF的长为 .
(2)如图2,当AE=1时,求点F到AD的距离和BF的长.
(3)当BF最短时,请直接写出此时AE的长.
21.在平行四边形ABCD中,,连接,已知,点在线段上,将线段绕点顺时针旋转为线段.
(1)如图1,线段与线段的交点和点重合,连接,求线段的长度;
(2)如图2,点为延长线上一点,连接交于点,连接EG,若点H为线段的中点,求证:;
(3)如图3,在(2)的条件下,连接,延长交于点,连接,直接写出线段长度的最小值.
22.如图1,在矩形中,,,点为边上一动点,连结,作点关于直线的对称点,连结,,,,与交于点.
(1)若,求证:.
(2)如图2,连结,,若点在矩形的对角线上,求所有满足条件的的长.
(3)如图3,连结,当点到矩形一个顶点的距离等于2时,请直接写出的面积.
23.在正方形中,点是边上点,点在的延长线上,将线段绕点顺时针旋转,到线段,连接.
(1)如图,连接,判断线段与线段的数量关系给出证明.
(2)如图,若正好经过点.
①直接用等式表示线段、和的数量关系为______.
②证明:.
(3)如图,当经过点时,若,,请直接写出此时正方形边的长度.
24.如图1,四边形为菱形,.,,.
(1)点A坐标为 ,四边形的面积为 ;
(2)如图2,点E在线段上运动,为等边三角形.
①求证:,并求的最小值;
②点E在线段上运动时,点F的横坐标是否发生变化?若不变,请求出点F的横坐标.若变化,请说明理由.
25.在矩形中,,,E、F是直线上的两个动点,分别从A、C两点同时出发相向而行,速度均为每秒2个单位长度,运动时间为t秒,其中.
(1)如图1,M、N分别是中点,当四边形是矩形时,求t的值;
(2)若G、H分别从点A、C沿折线,运动,与相同的速度同时出发.
①如图2,若四边形为菱形,求t的值;
②如图3,作的垂直平分线交于点P、Q,当四边形的面积是矩形面积的时,则t的值是______.
答案
一、单选题
1.D
【分析】过点作,由正方形的性质,,,四边形为矩形,利用HL易证得,可得,进而可得,由角平分线可得的度数,即可求得得度数.
【解析】解:过点作,
∵四边形是正方形,
∴,,
∵,则四边形为矩形,
∴,
∵,
∴(HL),
∴,
∵,
∴,
又∵平分,
∴,
∴.
故选:D.
2.C
【分析】连接,过作,利用面积法求解,的值等于点到的距离,即正方形对角线的一半.
【解析】解:连接,过作,如图所示:
,
,
,
四边形是正方形,
,,,
,
,,
为中点,
,
即值是.
故选:C.
3.B
【分析】过作于,由矩形的性质并结合勾股定理确定,再证明以及为等腰三角形,即可推导,,然后由计算的长即可.
【解析】解:过作于,
∵四边形是矩形,
∴,,,
∵,
∴,
∵,,
∴,
∴,
∴,
∵平分交于点,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∵为等腰三角形,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
故选:B.
4.A
【分析】先证明是等边三角形,求出EF,同理可证都是等边三角形,然后求出EH,GF,FG即可.
【解析】解:如图,连接BD,AC,
∵四边形ABCD是菱形,,
∴,,
∴,
∴,
∵,
∴,
在中,,,
∵在和 BFO中,
,
∴,
∴,
∵,
∴是等边三角形,
∴,
同法可证,都是等边三角形,
∴,,
∴四边形EFGH的周长为.
故选:A.
5.D
【分析】根据矩形的性质得到AB=CD,AB//CD,∠DAE=∠BCF=90°,OD=OB=OA=OC,AD=BC,AD//BC,根据平行线的性质得到DE⊥AC,根据垂直的定义得到∠DNA=∠BMC=90°,由全等三角形的性质得到DN=BM,∠ADE=∠CBF,故①正确;证△ADE≌△CBF(ASA),得出AE=FC,DE=BF,故③正确;证四边形NEMF是平行四边形,得出EM//FN,故②正确;证四边形DEBF是平行四边形,证出∠ODN=∠ABD,则DE=BE,得出四边形DEBF是菱形;故④正确;即可得出结论.
【解析】解:∵四边形ABCD是矩形,
∴AB=CD,AB//CD,∠DAE=∠BCF=90°,OD=OB=OA=OC,AD=BC,AD//BC,
∴∠DAN=∠BCM,
∵BF⊥AC,DE//BF,
∴DE⊥AC,
∴∠DNA=∠BMC=90°,
在△DNA和△BMC中,
,
∴△DNA≌△BMC(AAS),
∴DN=BM,∠ADE=∠CBF,故①正确;
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=FC,DE=BF,故③正确;
∴DE -DN=BFBM,即NE=MF,
∵DE//BF,
∴四边形NEMF是平行四边形,
∴EM//FN,故②正确;
∵AB=CD,AE=CF,
∴BE=DF,
∵BE//DF,
∴四边形DEBF是平行四边形,
∵AO=AD,
∴AO=AD=OD,
∴△AOD是等边三角形,
∴∠ADO=∠DAN=60°,
∴∠ABD=90°-∠ADO=30°,
∵DE⊥AC,
∴∠ADN=∠ODN=30°,
∴∠ODN=∠ABD,
∴DE=BE,
∴四边形DEBF是菱形;故④正确;
故选:D.
6.C
【分析】①由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ABD的中位线,得出OG=AB,①正确;
③先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;
②连接FD,由等边三角形的性质和角平分线的性质得F到△ABD三边的距离相等,则S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF,则S四边形ODGF=S△ABF,②错误;即可得出结论.
④∵连接CG,由O、G分别是AC,AD的中点,得到,则S△ACD=4S△AOG,再由S△AOG=S△BOG,得到S△ACD=4S△BOG,故④正确;
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ABD的中位线,
∴OG=AB,故①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴平行四边形ABDE是菱形,故③正确;
∵连接CG,
∵O、G分别是AC,AD的中点,
∴,
∴S△ACD=4S△AOG,
∵,
∴S△AOG=S△BOG,
∴S△ACD=4S△BOG,故④正确;
连接FD,如图:
∵△ABD是等边三角形,AO平分∠BAD,BG平分∠ABD,
∴F到△ABD三边的距离相等,
∴S△BDF=S△ABF=2S△BOF=2S△DOF=S四边形ODGF,
∴S四边形ODGF=S△ABF,故②错误;
正确的是①③④,
故选C.
7.B
【分析】由“”可证,可得,故正确;
如图,在上截取连接,由“”可证,可得,由“”可证,可得,
,故正确;
如图2,将绕点顺时针旋转,得到,连接,由旋转的性质可得,,,由“”可证,可得,由勾股定理可得,故正确;
如图1,设,则,利用勾股定理可求,故错误;
由三角形的面积公式可求,故正确;
【解析】解:四边形是正方形,
,,
,
,
,
故正确;
如图1,在上截取,连接,
,,,
,
,,
,
,
,
又,,
,
,,
故正确;
如图2,将绕点顺时针旋转,得到,连接,
,,
,,,
∵∠ABD=∠ADB=450,
,,
,
,
又,,
,
,
在中, ,
,
故正确;
,
设,则,
,
如图1,在上截取,连接,
由可得:,
设,则,
,
,
,
,
,
故错误;
如图1,,
,
,
故正确;
正确的结论有,共个.
故选:
8.C
【解析】试题分析:①连接AC,交BD于点O,∵四边形ABCD是菱形,∴AB=BC,BD⊥AC,AO=BO,∴点A,点C关于直线BD对称,∴M点与O点重合时AM+CM的值最小为AC的值,∵∠ABC=60,∴△ABC是等边三角形,∴AB=AC,∵AB=1,∴AC=1,即AM+CM的值最小为1,故本答案正确;
②∵△ABE是等边三角形,∴BA=BE,∠ABE=60°,∵∠MBN=60°,∴∠MBN﹣∠ABN=∠ABE﹣∠ABN,即∠MBA=∠NBE,又∵MB=NB,∴△AMB≌△ENB(SAS),故本答案正确;
③∵S△ABE+S△ABM=S四边形AMBE,S△ACD+S△AMC=S四边形ADCM,且S△AMB≠S△AMC,∴S△ABE+S△ABM≠S△ACD+S△AMC,∴S四边形AMBE≠S四边形ADCM,故本答案错误;
④假设AN⊥BE,且AE=AB,∴AN是BE的垂直平分线,∴EN=BN=BM=MA,∴M点与O点重合,∵条件没有确定M点与O点重合,故本答案错误;
⑤如图,连接MN,由(1)知,△AMB≌△ENB,∴AM=EN,∵∠MBN=60°,MB=NB,∴△BMN是等边三角形,∴BM=MN,∴AM+BM+CM=EN+MN+CM,根据“两点之间线段最短”,得EN+MN+CM=EC最短,∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.过E点作EF⊥BC交CB的延长线于F,∴∠EBF=180°﹣120°=60°,设菱形的边长为x,∴BF=,EF=,在Rt△EFC中,∵,∴,解得x=2,故本答案正确.
综上所述,正确的答案是:①②⑤,故选C.
9.C
【分析】本题综合考查了正方形的性质,全等三角形的性质,能够合理选择正方形的性质找到全等三角形是解题的关键.
①利用正方形的性质证明得到进而可证;②利用正方形的性质证明,得到,证明,进而可证;③求得的长度,然后求出,进而可证;④证明垂直平分,过点作,利用垂线段最短可知的长度为最小值,利用等面积法可求.
【解析】∵正方形,
∴, ,
∴,
在和中,
,
∴,
∴,
,
∴,
∴,故①正确;
∵平分,
∴,
在和中,
,
∴,
∴,
∵正方形,
∴,
∴,
∴,
∵,
∴,
∴,
∴,故②正确;
∵,
∴
,
,
,
即,结论③错误;
,
,
,
∴垂直平分,
,
当时,有最小值,
过点作,
则的长度为的最小值,
,
即的最小值为,故④正确.
正确的为: ①②④,个数为3
故选:C
10.C
【分析】由四边形是矩形,线段绕点逆时针旋转得到,可证,故①正确;当点和点互相重合时,由是等腰直角三角形,是的中点,,可得∠AED=450 =∠ADE,从而,故②正确;由等腰直角三角形的三线合一和得,从而得到,故③错误;分别求出的最大值、最小值,可得,故④正确.
【解析】解:四边形是矩形,
,
线段绕点逆时针旋转得到,
,∠AED=450 =∠ADE,
,
,
,
,故①正确;
当点和点互相重合时,如图,
线段绕点逆时针旋转得到,
,,
是等腰直角三角形,
是的中点,,
,
,
,
,故②正确;
线段绕点逆时针旋转得到,
,
是的中点,,
,
,故③错误;
当与重合时,最短,如图:
,
此时与都在上,
是等腰直角三角形,是的中点,
是等腰直角三角形,
,
,
,
的最小值为,
当与重合时,最大,过作于,如图:
,
,
,
,,,
,
设,则,
,
,
解得:(舍去)或,
,
,
,
的最大值为,
,故④正确;
综上所述,正确的有①②④,共3个,
故选:C.
二、填空题
11.③④
【分析】①根据正方形的性质及等腰三角形的判定,可得出图中共有9个等腰三角形;②根据正方形的性质和已知推出四边形DECB是平行四边形,得到BD=CE,BD∥CE,无法证出G为CE的中点;③由SAS可证明△GHC≌△DGE;④由上述推理可得,△DBG∽△GDE,再根据三角形的面积等于相似比的平方可得结论.
【解析】解:如图,在正方形中,
,,
和是等腰三角形;
,,
和是等腰三角形;
,,
,
,
∵ BCG和是等腰三角形;
,,
是等腰三角形,且,,
,,
∵ DHG和是等腰三角形,
综上,图中共有9个等腰三角形;故①不正确;
正方形,,
,,,
四边形是平行四边形,
,,
,
,
要使,只要为的中点即可,
且,,
,
即和不全等,
点不是中点,②错误
由①分析可知,
在和中,
,
;故③正确;
如图,过点作交的延长线于点,交AF于N,
设NG=x,则MG=1-x,
∵△CDE为等腰三角形,
∴∠DCE=∠DEC=45°,
可得△CGM为等腰直角三角形,
∴CM=1-x,
∴CG=,
设正方形ABCD的边长为1,
则BC=DE=1,BD=DF=CE=,
∵△BCG为等腰三角形,
∴,
解得:,
∴,故④正确;
综上,③④正确.
故答案为:③④.
12.①③
【分析】连接,由菱形的性质得出,,,,得出是等边三角形,得出,,证明得出,证出是等边三角形,得出②不正确, 的面积的面积,得出的面积,①正确,当时,最小,等边的面积最小,求出的面积,得出,③正确;即可得出结论.
【解析】解:连接,如图所示:
四边形是菱形,
,,,,
是等边三角形,
,,
,
,
在和中,
,
,
,
是等边三角形,②不正确, 的面积的面积,
的面积,①正确,
当时,最小,等边的面积最小,
的面积,
,③正确;
故答案为:①③.
13.②
【分析】①设AF=CF=x,构建方程求出x即可判断;②证明∠BAC=90°,利用勾股定理求出AC,求出平行四边形ABCD的面积即可判断;③当AE⊥BC时,四边形ABEC是等腰梯形,不符合题意.
【解析】解:①如图1中,
∵∠B=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠DAC=∠CAE,
∴∠ACF=∠CAF,
∴AF=CF,设AF=CF=x,
在Rt△ABF中,则有x2=62+(8-x)2,
解得x=,
∴EF=8-=,故错误;
如图2中,
当BF=CF时,
∵AF=CF=BF,
∴∠BAC=90°,
∴AC=,
∴S平行四边形ABCD=AB AC=6×=,故正确;
如图3中,
当AE⊥BC时,四边形ABEC是等腰梯形,故错误.
故答案为:②.
14.
【分析】先根据题意求得,如图,过点作,则可的是等边三角形,由可得,,则,,进而根据AAS可证明,进而可得的长,过点作于点,过作于,根据勾股定理可得的长,设,进而求得的长由,可得是等边三角形,进而求得,根据的面积等于,据此列出方程,解方程即可求得,进而求得.
【解析】如图,过点作,
四边形是菱形,
,是等边三角形
是等边三角形
,
,
即
在和中
(AAS)
,
是等边三角形,
过点作于点,过作于,如图,
在中,
在中,
在中,设,
是等边三角形,
的面积等于
整理得
因式分解得:
解得或(舍)
故答案为:
15.
【分析】根据“等腰四边形”的定义画出图形,对角线是该四边形的“等腰线”,所以和为等腰三角形,由于,中分两种情形:①,②.当时,由于,可得为等边三角形,,则,结论可得;当时,过点作,根据等腰三角形的三线合一,,过点作,交延长线于点,根据四边形为矩形,,可得,由于,可得,从而可求.
【解析】解:凸四边形是“等腰四边形”,对角线是该四边形的“等腰线”,
和为等腰三角形.
由于,在中分两种情形:①,②.
当①时,如下图:
,.
.
为等边三角形.
.
,
.
,
.
当②时,如下图,
过点作,过点作,交延长线于点,
,,
.
,,,
四边形为矩形.
.
,
.
在中,,
.
,
.
,
.
,
.
综上,.
故答案为:.
16.
【分析】连接,过点作的平行线交于点,过点作交延长线于点,延长交于点,过点作于点,利用翻折的性质和勾股定理求出,然后证明,得,证明,再利用勾股定理求出,进而即可解决问题.
【解析】解:如图,连接,过点作的平行线交于点,过点作交延长线于点,延长交于点,过点C作于点,
由翻折可知:,
∵点是的中点,,为菱形,
∴,
设,
在中,,
由勾股定理得:,
整理得,
解得(舍去负值),
∵HI∥BC∥AD,
∵∠AEK=∠HEI,
由翻折可知:,
∵BC∥AD,
设
∵CL⊥AD,∠D=600 ,CD=12 ,
在中,由勾股定理得:
故答案为:.
17.1或
【分析】存在三种情况:当时,连接ED,利用勾股定理可以求得ED的长,可判断三点共线,根据勾股定理即可求解;当时,可以证得四边形是正方形,即可求解;当时,连接EC,FC,证明三点共线,再用勾股定理,即可求解.
【解析】解:①当时,连接ED,如图,
∵点E是的中点,,,四边形是矩形,
∴,
由勾股定理可得,,
∵将沿所在直线翻折,得到,
∴,
∵,
∴,
∴三点共线,
∵,
∴,
设,则,,
在中,,
∴,
解得,
∴;
②当时,如图,
∵,
∴点在线段CD的垂直平分线上,
∴点在线段AB的垂直平分线上,
∵点E是的中点,
∴是AB的垂直平分线,
∴,
∵将沿所在直线翻折,得到,
∴,
∴四边形是正方形,
∴;
综上所述,AF的长为1或.
故答案为:1或.
18. 1
【分析】(1)由于四边形ABCD为矩形,四边形HEFG为正方形,那么∠D=∠A=∠GHE=90°,HG=HE,易证△GDH≌△HAE,得DG=AH=1;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=1,进而可求△FCG的面积S的最大值和最小值,从而确定S的取值范围.
【解析】解:(1)如图1,当菱形为正方形时,,,
四边形为矩形,
,
,
,
在和中,
,
,
;
故答案为:1;
(2)如图2,过作,交延长线于,连接,
,
,
,
,
,
在和中,
,
,即无论菱形如何变化,点到直线的距离始终为定值1,
因此,
设,则,
在中,,
,
,
,
,
的最小值为,此时,的最大值为,此时,
在点的运动过程中,的面积的取值范围为:;
故答案为:;
三、解答题
19.解:(1)如图1中,
,,
,
,
.
(2)如图2中,
,
可以假设,,则
,,
,
,,
.
(3)如图3中,过点作于,过点作于.
,
可以假设,,
∵AC⊥BD,
,,,,
,,
,
,
,
,
,
,
,
,
,
,
四边形是矩形,
,,
,
,
整理得,
,
,
经检验:符合题意;
.
20.解:(1)如图,连接DF,
∵∠CAF=90°,∠CAD=45°,
∴∠DAF=45°,
在△CAD和△FAD中,
,
∴△CAD≌△FAD(SAS),
∴DF=CD,
∴∠ADC=∠ADF=90°,
∴C,D,F共线,
∴BF2=BC2+CF2=42+82=80,
∴BF=,
故答案为:;
(2)如图,过点F作FH⊥AD交AD的延长线于点H,FH⊥BC交BC的延长线于K,
∵四边形CFG是正方形,∴EC=EF,∠FEC=90°,
∴∠DEC+∠FEH=90°,
又∵四边形ABCD是正方形,
∴∠ADC=90°,
∴∠DEC+∠ECD=90°,
∴∠ECD=∠FEH,
又∵∠EDC=∠FHE=90°,
在△ECD和△FEH中,
,
∴△ECD≌△FEH(AAS),
∴FH=ED,
∵AD=4,AE=1,
∴ED=AD -AE=4-1=3,
∴FH=3,即点F到AD的距离为3,
∴∠DHK=∠HDC=∠DCK=90°,
∴四边形CDHK为矩形,
∴HK=CD=4,
∴FK=FH+HK=3+4=7,
∵△ECD≌△FEH,
∴EH=CD=AD=4,
∴AE=DH=CK=1,
∴BK=BC+CK=4+1=5,
在Rt△BFK中,BF=;
(3)∵当A,D,F三点共线时,BF的最短,
∴∠CBF=45°,
∴FH=DH,
由(2)知FH=DE,EH=CD=4,
∴ED=DH=4÷2=2,
∴AE=2.
21.(1)延长,过点作于点,过点作于点,过点作于点,于点,
∴,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∵四边形是平行四边形,
∴,,,,,,
∴,,,
∴是等腰直角三角形,
∴,,
∴,
∵线段绕点顺时针旋转为线段,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,,
∴,
∵,
∴四边形是矩形,
∴,,
∴,
∴.
(2)连接、、,
∵四边形是平行四边形,
∴,,
由(1)得,,,
∴,
∴点、、、四点共圆,
∴,
∴点在的延长线上,
∴,
∴,
∵点为线段的中点,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
∵,,
∴,
∴.
(3)连接,,,,
由(2)得,,点为的中点,,
∴,
∵,,
∴,
∴,
∴,
∵点为的中点,,
∴,
∴,
∵,,
∴,
∵(当且仅当点在线段上时等号成立),
∴,
∴的最小值为.
22.(1)证明:∵点关于的对称点为点,
∴,即点为的中点.
∵,,
∴点为的中点,
∴为的中位线.
∴.
(2)分两种情况:
①如图1,点在对角线上.
∵点关于的对称点为点,
∴,,.
∴AC=5
设,
∴,
∴,即.
②如图2,点在对角线上.
∵,,
∴.
∵S△ABD=
∴.
∴.
设,,
∵DG2+GE2=DE2,
∴
∵S△ADE=
∴
∴.
∴,即.
综上:或.
(3)分三种情况:
①点到矩形顶点A的距离等于2时
∵AF=AD=3>2
∴此种情况不存在;
②当点到矩形顶点的距离等于2时,连接FB,
则BF=2,AF=AD=3
过F作FH⊥AB于H,FQ⊥BC于Q,如图,
∴∠FHB=∠ABC=∠BQF=90°
∴四边形BHFQ是矩形
∴FQ=BH
设BH=x,则AH=4-x
∵FH2=AF2-FH2=FB2-BH2
∴4-x2=9-(4-x)2
∴x=
∴FQ=BH=
∴的面积为=.
③当点到矩形顶点的距离等于2时,如图,连接BF
则FC=2
∵AF+FC≥AC,又AF+FC=5,AC=5
∴AC+FC=AC
∴A,C,F三点共线,F在线段AC上
∵
∴=
即的面积为.
④当点到矩形顶点的距离等于2时,连接BF,过F点作MNAB
则DF=2
∴DG=FG=1
∴AG=
∵
∴MF=
∴NF=MN -MF=4-
∴的面积为=.
综上①当点到矩形顶点的距离等于2时,的面积为;②当点到矩形顶点的距离等于2时,的面积为;③当点到矩形顶点的距离等于2时,的面积为.
23.(1)解:,
证明:四边形是正方形,
,,
将线段绕点顺时针旋转,到线段,
,,
,
≌,
;
(2)解:;
理由如下:如图,连接,
四边形是正方形,
,,
,
,
,
,
;
故答案为:;
证明:,,
,
≌ ADE,
,
,
;
(3)解:如图,连接,过点作于,
,,
,
,,,
,
,
,
,
,
正方形的边长为.
24.(1)解:∵,,,
∴,,
∵四边形为菱形,
∴,,
∴,
∴,
∴,
故答案为:,;
(2)①证明:如图,设交于J.
∵四边形是菱形,
∴,,,
∴,都是等边三角形,
∴,
∴.
∵,
∴,
∴,
∴当时,的值最小.
∵,
∴,
∴
∴AF的最小值为.
②点F的横坐标不变,理由如下:
如图,过点F作于H.
∵,
∴.
∵,
∴,
∴,
∴点F的横坐标为,不变.
25.(1)解:∵四边形是矩形,
∴,,
∴,
∵M、N分别是的中点,
∴,
∵E、F分别从A、C同时出发相向而行,速度均为每秒2个单位长度,
∴,
∴,
∴,,
∴,
∴,
∴四边形是平行四边形,
如图1,连接,
∵四边形是矩形,M,N分别是中点,
∴,,
∴四边形是平行四边形,
∵∠B=900,
∴四边形是矩形,
∵矩形中,,,
∴,,
∵四边形是平行四边形,
∴当时,四边形是矩形,
∴或,
解得:或;
(2)①由(1)知:,
如图2,连接,
∵四边形为菱形,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
②如图3,连接,
由①同理得:,,
由①知:,
∴,
∵G、H分别从点A、C沿折线,运动,
∴,
又∵,
∴,
∴,
同理可证,
∴四边形是平行四边形,
∵四边形的面积是矩形面积的,
∴,
∴,
∴,
∴,
∴,
∴,
∴.
故答案为:.
