2.2简谐运动的描述 课件(共43张PPT)2024-2025学年人教版高中物理选择性必修 第一册
文档属性
| 名称 | 2.2简谐运动的描述 课件(共43张PPT)2024-2025学年人教版高中物理选择性必修 第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 18.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-13 14:18:49 | ||
图片预览










文档简介
(共43张PPT)
教
学
课
件
2.2简谐运动的描述
第二章 机械振动
简谐运动的位移时间关系
振幅
圆频率
周期和频率
01
02
03
04
目录
CONTENTS
相位
05
简谐运动的位移时间关系
PART 1
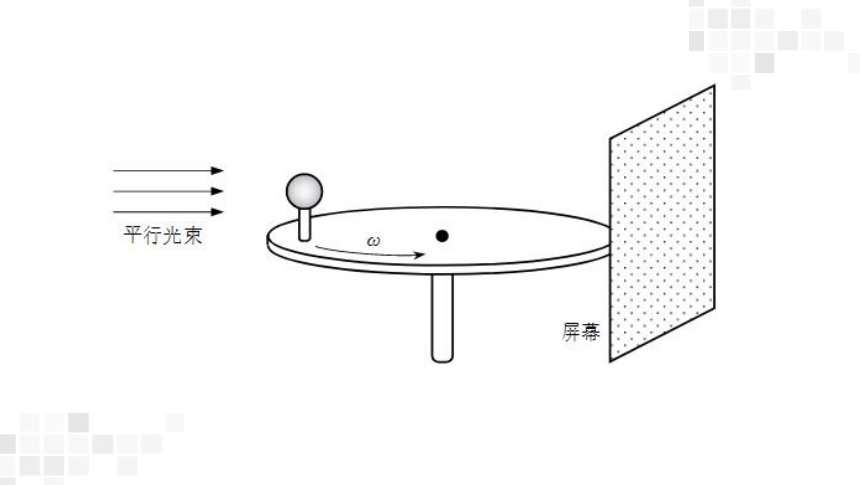
上一节我们学习了如果物体的位移与时间的关系遵从正弦函数的规律,即它的振动图像(x-t 图像)是一条正(余)弦曲线,这样的振动是一种简谐运动。
我们用什么样的方式来表达简谐运动?
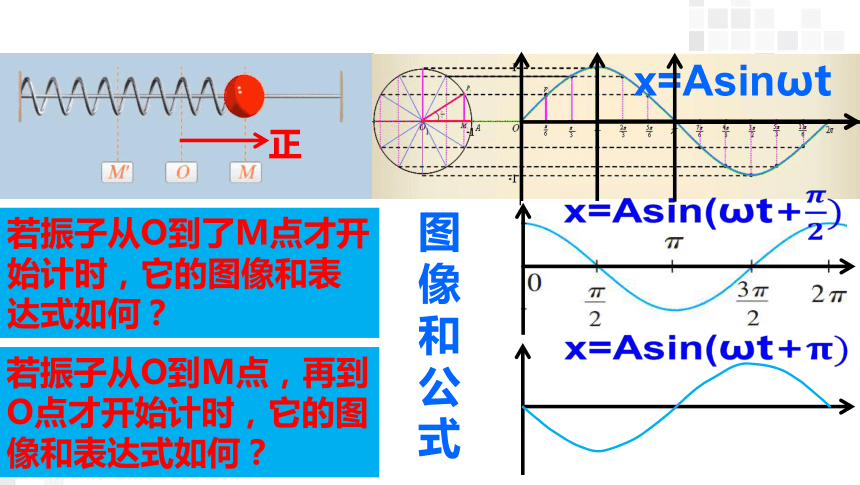
若振子从O到了M点才开始计时,它的图像和表达式如何?
正
x=Asinωt
图像和公式
x=Asin(ωt+
若振子从O到M点,再到O点才开始计时,它的图像和表达式如何?
x=Asin(ωt+
一、简谐运动的位移时间关系
1.定义式:
注意:
x=
x-t是正弦函数的振动必是简谐运动
Asin(ωt+
2.全振动:
两次以相同的速度经过同一点时,我们称物体完成了一次全振动。
因为∣sin(ωt+)∣≤ 1,所以∣x ∣≤ A,这说明A是物体离开平衡位置的最大距离。
振幅
PART 2
1.定义:离开平衡位置的最大距离,单位(m)
2.物理意义:反映振动强弱的物理量。
能静止位置
振幅
振幅
:即平衡位置
①位移时刻在变化;但振幅是不变的。
②位移是矢量,振幅是标量。
注意:对于一个确定的简谐运动
二、振幅
4.振幅的大小直接反映了振子振动能量(E=EK+EP)的高低。
3.振子振动范围的大小是振幅的两倍——2A;
振幅就是最大的位移对吗?
振幅是一个标量,指物体偏离平衡位置的最大距离。它没有负值,也无方向,所以振幅不同于最大位移。
一个弹簧振子振幅越大,能量越大对吗?
振幅与振动的能量有关,振幅越大,能量越大。
圆频率
PART 3
1.定义: 三角函数转圈的角速度,单位(rad/s)
x=Asin(ωt+
2.定义式:
ω=
=
3.周期T:
一次周期性振动时间,单位(s)
4.频率f:
单位时间内完成全振动的次数,单位(HZ)
5.物理意义:
反映振动快慢
思考:弹簧振子的周期和频率与什么因素有关呢?
三、圆频率
周期和频率
PART 4
1.猜想影响因数:
①振幅A ②小球质量m ③劲度系数k.
2.实验验证:
控制变量法
x=Asin(ωt+
1.实验结论:
周期由振动系统本身质量和劲度系数决定,与振幅无关,所以常把周期和频率叫做固有周期和固有频率
T=
2.固有周期:
=
四、周期和频率
3.在简谐运动中,振幅跟频
率或周期无关。
简谐运动是一种周期性的运动,简谐运动的物理量随时间
周期性变化,如图所示,物体在A、B两点间做简谐运动,
O点为平衡位置,OC=OD。
(1)时间的对称
①物体来回通过相同两点间的时间相等,即tDB=tBD。
②物体经过关于平衡位置对称的等长的两段路程的时间相等,图中tDB=tBD=tCA=tAC,tOD=tDO=tOC=tCO。
4.简谐运动的对称性
(2)速度的对称
①物体连续两次经过同一点(如D点)的速度大小相等,方向相反。
②物体经过关于O点对称的两点(如C点与D点)时,速度大小相等,方向可能相同,也可能相反。
第二部分 点击在此输入你的标题内容
(3)位移的对称
①物体经过同一点(如C点)时,位移相同。
②物体经过关于O点对称的两点(如C点与D点)时,位移大小相等、方向相反。
一次全振动通过的路程是几个振幅?半个周期内通过几个振幅?
5.路程与振幅
(1)振动物体在一个周期内的路程为四个振幅,
即4A。
(2)振动物体在半个周期内的路程为两个振幅,
即2A。
四分之一周期内通过几个振幅?
以刚才的例子为例
(3)只有当初始时刻振动物体在平衡位置或最大位移处时,个周期内的路程才等于一个振幅。
(4)当初始时刻振动物体不在平衡位置或最大位移处时,若质点开始时运动的方向指向平衡位置,则质点在个周期内的路程大于A,若质点开始时运动的方向远离平衡位置,则质点在个周期内的路程小于A。
例1.如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2 s内经过的路程为5.6 m。该弹簧振子的周期为________s,振幅为________m。
4
2.8
0.3s
例2. 如图所示,一弹簧振子做简谐运动,O点为平衡位置,当振子经过O点时开始计时,(M为O点右侧一个位置)则:
(1)振子先向右运动经0.3 s第一次过M点,再经0.2 s 第二次过M点。振子振动周期为多大?
(2)振子先向左运动经0.3 s第一次过M点,
再经0.2 s 第二次过M点,振子振动
周期为多大?
0.2s
0.1s
解(1)
得:T=1.6S
(2)
0.3s
0.1s
0.2s
得:T=
=
例3.(多选)物体做简谐运动,通过A点时的速度为v,经过时间t后物体第一次以相同速度v通过B点,又经过同样的时间物体紧接着又通过B点,已知物体在这段时间内走过的总路程为18 cm,则该简谐运动的振幅可能是( )
A.3 cm
B.5 cm
C.7 cm
D.9 cm
O
A
B
V
t
t/2
18cm
2A=18cm
A=9cm
O
A
B
V
6A=18cm
A=3cm
AD
思考3:对于一个制作好的弹簧振子,什么确定了
周期T、和频率f
思考4:对于一个振动起来的弹簧振子,什么确定了
振幅A、圆频率
x=Asin(ωt+
思考5:对于一个振动起来的弹簧振子,什么一直变
位移x、
速度v、加速度a、回复力F回
相位
当(ωt+φ)确定时,sin(ωt+φ)的值也就确定了,所以(ωt+φ)代表了物体此时正处于一个运动周期中的哪个状态。
相位
PART 5
当(ωt+)确定时,sin(ωt+)的值就确定了,所以(ωt+)代表了做简谐运动的物体此时正处于一个周期运动中的哪一个状态。
正弦函数 x= A sin(ωt+)
A
-A
五、相位
1、定义:物理学中把x=Asin(ωt+φ)中的 (ωt+φ)叫做相位。(每个时刻对应的对应角度(ωt+φ))
2、物理意义:反映振动物体所处的运动状态。相位不同所处的运动状态不同。
3. 是t=0时的相位,称作初相位,简称初相。(t=0时的对应角度φ)
4.相位差:
Δφ=(ω1t+φ1 )-(ω2t+φ2)= 2
注意:两个f相同的简谐运动的相位差恒定不变。
2时,常说1的相位比2超前△,或者说2的相位比1落后△。
s
x=10sin(2πt+π/2)
例4.一弹簧振子的位移随时间变化的图线如下图所示,试写出相应的函数表达式。
例5.某简谐运动的位移与时间关系为:x=0.1sin(100πt+π )cm, 由此可知该振动的振幅是______cm,频率是 Hz,零时刻振动物体的速度与规定正方向_____(填“相同”或“相反”).
0.1
50
相反
例6.(多选)(2022·广州六中月考)物体A做简谐运动的振动位移xA=3sin(100t+) m,物体B做简谐运动的振动位移xB=5sin(100t+) m。以下说法正确的是( )
A.物体A的振幅是6 m,物体B的振幅是10 m
B.物体A、B的周期相等,为100 s
C.物体A振动的频率fA等于物体B振动的频率fB
D.物体A的相位始终超前物体B的相位
CD
例7.(2024河南南阳联考)如图所示为甲、乙两个质点做简
谐运动的振动图像,实线为甲的振动图像,虚线为乙的振动
图像,其中甲的振动方程为x=3a sin (5πt)。下列说法中正
确的是 ( )
A.甲质点的振幅是a
B.甲质点振动的频率是5π Hz
C.t=0时,甲、乙的相位差是π/2
D.t=0时,甲、乙的相位差是3π/4
C
例8.甲、乙两物体各自做简谐运动,某时刻开始计时,它们
的振动方程分别为x甲=3a sin ( 4πbt+π/4 ),
x乙=2a sin (8πbt+π/2),下列说法正确的是( )
A.甲、乙的振幅之比为2∶3
B.甲、乙的振动频率之比为2∶1
C.各自的一个周期内,甲、乙运动的路程之差为4a
D.t=0时,甲、乙的相位差为3π/4
C
例9.弹簧振子做简谐运动,振子的运动范围为0.8m,周期为0.5s,开始计时时具有正向最大加速度,则它的振动方程为( )
A.x=810-3sin(4t+)(m)
B.x=410-3sin(4t - )(m)
C.x=810-3sin(2t+)(m)
D.x=410-3sin(2t -)(m)
B
例10.(2021·广东·高考真题)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经时间,小球从最低点向上运动的距离_______(选填“大于”“小于”或“等于”);在时刻,小球的动能________(选填“最大”或“最小”)。试写出此振动的振动方程________________________
最大
小于
y=Asin(+
sinθ
θ
2
A
-A
谢
谢
聆
听
教
学
课
件
2.2简谐运动的描述
第二章 机械振动
简谐运动的位移时间关系
振幅
圆频率
周期和频率
01
02
03
04
目录
CONTENTS
相位
05
简谐运动的位移时间关系
PART 1
上一节我们学习了如果物体的位移与时间的关系遵从正弦函数的规律,即它的振动图像(x-t 图像)是一条正(余)弦曲线,这样的振动是一种简谐运动。
我们用什么样的方式来表达简谐运动?
若振子从O到了M点才开始计时,它的图像和表达式如何?
正
x=Asinωt
图像和公式
x=Asin(ωt+
若振子从O到M点,再到O点才开始计时,它的图像和表达式如何?
x=Asin(ωt+
一、简谐运动的位移时间关系
1.定义式:
注意:
x=
x-t是正弦函数的振动必是简谐运动
Asin(ωt+
2.全振动:
两次以相同的速度经过同一点时,我们称物体完成了一次全振动。
因为∣sin(ωt+)∣≤ 1,所以∣x ∣≤ A,这说明A是物体离开平衡位置的最大距离。
振幅
PART 2
1.定义:离开平衡位置的最大距离,单位(m)
2.物理意义:反映振动强弱的物理量。
能静止位置
振幅
振幅
:即平衡位置
①位移时刻在变化;但振幅是不变的。
②位移是矢量,振幅是标量。
注意:对于一个确定的简谐运动
二、振幅
4.振幅的大小直接反映了振子振动能量(E=EK+EP)的高低。
3.振子振动范围的大小是振幅的两倍——2A;
振幅就是最大的位移对吗?
振幅是一个标量,指物体偏离平衡位置的最大距离。它没有负值,也无方向,所以振幅不同于最大位移。
一个弹簧振子振幅越大,能量越大对吗?
振幅与振动的能量有关,振幅越大,能量越大。
圆频率
PART 3
1.定义: 三角函数转圈的角速度,单位(rad/s)
x=Asin(ωt+
2.定义式:
ω=
=
3.周期T:
一次周期性振动时间,单位(s)
4.频率f:
单位时间内完成全振动的次数,单位(HZ)
5.物理意义:
反映振动快慢
思考:弹簧振子的周期和频率与什么因素有关呢?
三、圆频率
周期和频率
PART 4
1.猜想影响因数:
①振幅A ②小球质量m ③劲度系数k.
2.实验验证:
控制变量法
x=Asin(ωt+
1.实验结论:
周期由振动系统本身质量和劲度系数决定,与振幅无关,所以常把周期和频率叫做固有周期和固有频率
T=
2.固有周期:
=
四、周期和频率
3.在简谐运动中,振幅跟频
率或周期无关。
简谐运动是一种周期性的运动,简谐运动的物理量随时间
周期性变化,如图所示,物体在A、B两点间做简谐运动,
O点为平衡位置,OC=OD。
(1)时间的对称
①物体来回通过相同两点间的时间相等,即tDB=tBD。
②物体经过关于平衡位置对称的等长的两段路程的时间相等,图中tDB=tBD=tCA=tAC,tOD=tDO=tOC=tCO。
4.简谐运动的对称性
(2)速度的对称
①物体连续两次经过同一点(如D点)的速度大小相等,方向相反。
②物体经过关于O点对称的两点(如C点与D点)时,速度大小相等,方向可能相同,也可能相反。
第二部分 点击在此输入你的标题内容
(3)位移的对称
①物体经过同一点(如C点)时,位移相同。
②物体经过关于O点对称的两点(如C点与D点)时,位移大小相等、方向相反。
一次全振动通过的路程是几个振幅?半个周期内通过几个振幅?
5.路程与振幅
(1)振动物体在一个周期内的路程为四个振幅,
即4A。
(2)振动物体在半个周期内的路程为两个振幅,
即2A。
四分之一周期内通过几个振幅?
以刚才的例子为例
(3)只有当初始时刻振动物体在平衡位置或最大位移处时,个周期内的路程才等于一个振幅。
(4)当初始时刻振动物体不在平衡位置或最大位移处时,若质点开始时运动的方向指向平衡位置,则质点在个周期内的路程大于A,若质点开始时运动的方向远离平衡位置,则质点在个周期内的路程小于A。
例1.如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2 s内经过的路程为5.6 m。该弹簧振子的周期为________s,振幅为________m。
4
2.8
0.3s
例2. 如图所示,一弹簧振子做简谐运动,O点为平衡位置,当振子经过O点时开始计时,(M为O点右侧一个位置)则:
(1)振子先向右运动经0.3 s第一次过M点,再经0.2 s 第二次过M点。振子振动周期为多大?
(2)振子先向左运动经0.3 s第一次过M点,
再经0.2 s 第二次过M点,振子振动
周期为多大?
0.2s
0.1s
解(1)
得:T=1.6S
(2)
0.3s
0.1s
0.2s
得:T=
=
例3.(多选)物体做简谐运动,通过A点时的速度为v,经过时间t后物体第一次以相同速度v通过B点,又经过同样的时间物体紧接着又通过B点,已知物体在这段时间内走过的总路程为18 cm,则该简谐运动的振幅可能是( )
A.3 cm
B.5 cm
C.7 cm
D.9 cm
O
A
B
V
t
t/2
18cm
2A=18cm
A=9cm
O
A
B
V
6A=18cm
A=3cm
AD
思考3:对于一个制作好的弹簧振子,什么确定了
周期T、和频率f
思考4:对于一个振动起来的弹簧振子,什么确定了
振幅A、圆频率
x=Asin(ωt+
思考5:对于一个振动起来的弹簧振子,什么一直变
位移x、
速度v、加速度a、回复力F回
相位
当(ωt+φ)确定时,sin(ωt+φ)的值也就确定了,所以(ωt+φ)代表了物体此时正处于一个运动周期中的哪个状态。
相位
PART 5
当(ωt+)确定时,sin(ωt+)的值就确定了,所以(ωt+)代表了做简谐运动的物体此时正处于一个周期运动中的哪一个状态。
正弦函数 x= A sin(ωt+)
A
-A
五、相位
1、定义:物理学中把x=Asin(ωt+φ)中的 (ωt+φ)叫做相位。(每个时刻对应的对应角度(ωt+φ))
2、物理意义:反映振动物体所处的运动状态。相位不同所处的运动状态不同。
3. 是t=0时的相位,称作初相位,简称初相。(t=0时的对应角度φ)
4.相位差:
Δφ=(ω1t+φ1 )-(ω2t+φ2)= 2
注意:两个f相同的简谐运动的相位差恒定不变。
2时,常说1的相位比2超前△,或者说2的相位比1落后△。
s
x=10sin(2πt+π/2)
例4.一弹簧振子的位移随时间变化的图线如下图所示,试写出相应的函数表达式。
例5.某简谐运动的位移与时间关系为:x=0.1sin(100πt+π )cm, 由此可知该振动的振幅是______cm,频率是 Hz,零时刻振动物体的速度与规定正方向_____(填“相同”或“相反”).
0.1
50
相反
例6.(多选)(2022·广州六中月考)物体A做简谐运动的振动位移xA=3sin(100t+) m,物体B做简谐运动的振动位移xB=5sin(100t+) m。以下说法正确的是( )
A.物体A的振幅是6 m,物体B的振幅是10 m
B.物体A、B的周期相等,为100 s
C.物体A振动的频率fA等于物体B振动的频率fB
D.物体A的相位始终超前物体B的相位
CD
例7.(2024河南南阳联考)如图所示为甲、乙两个质点做简
谐运动的振动图像,实线为甲的振动图像,虚线为乙的振动
图像,其中甲的振动方程为x=3a sin (5πt)。下列说法中正
确的是 ( )
A.甲质点的振幅是a
B.甲质点振动的频率是5π Hz
C.t=0时,甲、乙的相位差是π/2
D.t=0时,甲、乙的相位差是3π/4
C
例8.甲、乙两物体各自做简谐运动,某时刻开始计时,它们
的振动方程分别为x甲=3a sin ( 4πbt+π/4 ),
x乙=2a sin (8πbt+π/2),下列说法正确的是( )
A.甲、乙的振幅之比为2∶3
B.甲、乙的振动频率之比为2∶1
C.各自的一个周期内,甲、乙运动的路程之差为4a
D.t=0时,甲、乙的相位差为3π/4
C
例9.弹簧振子做简谐运动,振子的运动范围为0.8m,周期为0.5s,开始计时时具有正向最大加速度,则它的振动方程为( )
A.x=810-3sin(4t+)(m)
B.x=410-3sin(4t - )(m)
C.x=810-3sin(2t+)(m)
D.x=410-3sin(2t -)(m)
B
例10.(2021·广东·高考真题)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经时间,小球从最低点向上运动的距离_______(选填“大于”“小于”或“等于”);在时刻,小球的动能________(选填“最大”或“最小”)。试写出此振动的振动方程________________________
最大
小于
y=Asin(+
sinθ
θ
2
A
-A
谢
谢
聆
听
