代数式重点考点 归纳练 2025年中考数学一轮复习备考
文档属性
| 名称 | 代数式重点考点 归纳练 2025年中考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 425.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-13 15:50:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
代数式重点考点 归纳练
2025年中考数学一轮复习备考
一、单选题
1.(2022·云南楚雄·一模)下列计算正确的是( )
A.(a-1)2=a2-1 B.4a·2a=8a2
C.2a-a=2 D.a8÷a2=a4
2.(2022·广西贵港·中考真题)下面计算正确的是( )
A. B. C. D.
3.(22-23八年级上·四川广安·期末)下列算式,能按照“底数不变,指数相乘”计算的是( )
A. B. C. D.
4.(2022·广西贺州·中考真题)下列运算正确的是( )
A. B. C. D.
5.(2024·福建福州·模拟预测)下面的四个问题中,都有a,b两个未知量:
①有两杯水,一杯的水温b是另一杯水温a的3倍低
②土豆单价a比小米椒单价b的便宜2元
③某文具店的装订机的价格b比文具盒的价格a的3倍少6元
④有两根绳子,一根绳子的长度a比另一根绳子的长度b的3倍多6米其中,未知量b可以用表示的是( )
A.①② B.①③ C.②③ D.②④
6.(2024·浙江绍兴·二模)下列计算正确的是( )
A. B. C. D.
7.(2024·天津河东·一模)计算的结果正确的是( )
A. B. C. D.
8.(2024·安徽六安·模拟预测)下列运算中,结果正确的是( )
A. B.
C. D.
9.(2024·广东汕头·一模)若关于x,y的方程组的解满足,则的值为( )
A.8 B. C.6 D.
10.(2023·山东济南·二模)若,则代数式的值为( )
A.2 B. C. D.
11.(2022·浙江宁波·一模)已知a,b,c分别是的三条边长,c为斜边长,,我们把关于x的形如的一次函数称为“勾股一次函数”,若点在“勾股一次函数”的图象上,且的面积是4,则c的值是( )
A. B.24 C. D.12
二、填空题
12.(22-23七年级上·陕西安康·期末)如果与是同类项,那么 .
13.(23-24八年级上·江苏淮安·期中)若x,y为实数, 且 ,则 .
14.(2024·四川成都·模拟预测)若,则代数式的值为 .
15.(2022·湖北十堰·中考真题)如图,某链条每节长为,每两节链条相连接部分重叠的圆的直径为,按这种连接方式,50节链条总长度为 .
16.(2023·福建莆田·一模)求的值,可以采用下面方法:
解:令
由等式的基本性质二得:
由平方差公式得:
令
请仿照上面的推理,计算出: .
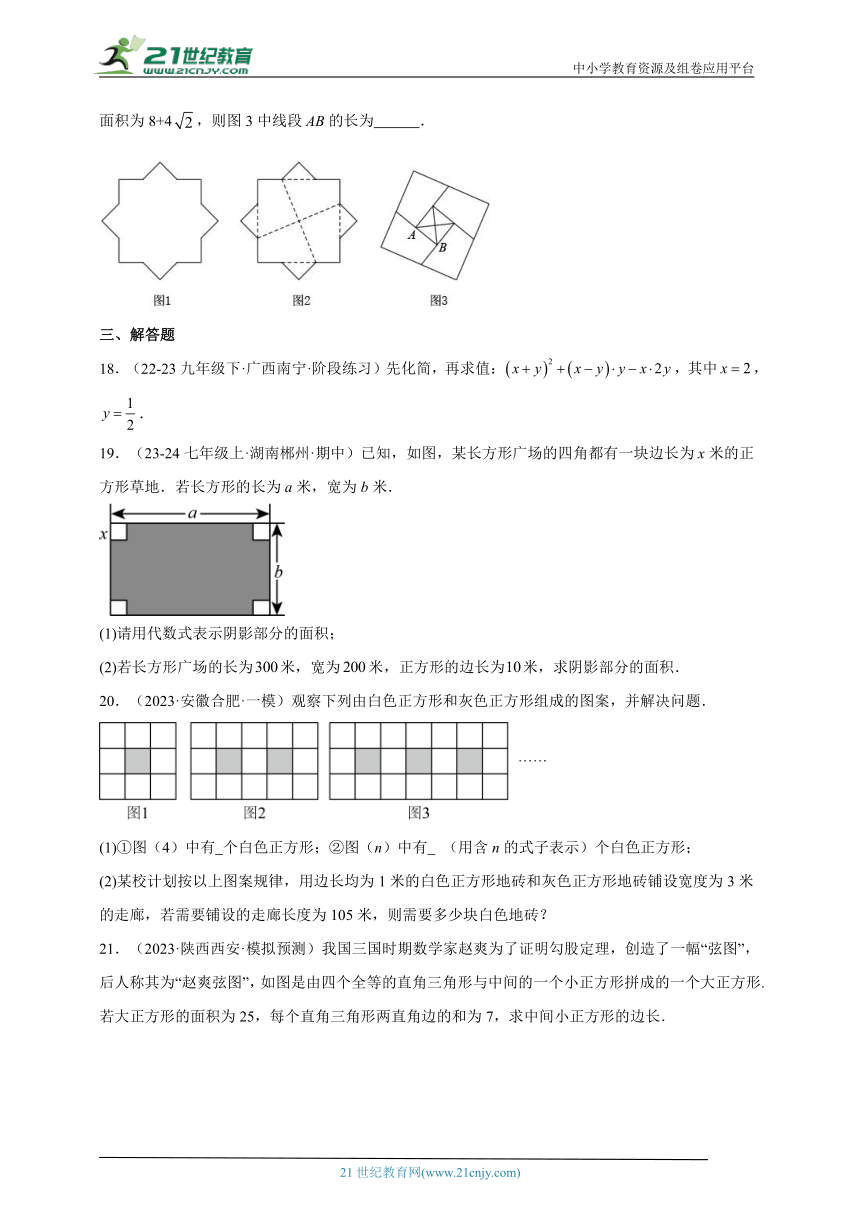
17.(11-12九年级上·湖北黄冈·期末)如图1是一个八角星纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成如图3所示的大正方形,其面积为8+4,则图3中线段AB的长为 .
三、解答题
18.(22-23九年级下·广西南宁·阶段练习)先化简,再求值:,其中,.
19.(23-24七年级上·湖南郴州·期中)已知,如图,某长方形广场的四角都有一块边长为x米的正方形草地.若长方形的长为a米,宽为b米.
(1)请用代数式表示阴影部分的面积;
(2)若长方形广场的长为米,宽为米,正方形的边长为米,求阴影部分的面积.
20.(2023·安徽合肥·一模)观察下列由白色正方形和灰色正方形组成的图案,并解决问题.
(1)①图(4)中有 个白色正方形;②图(n)中有 (用含n的式子表示)个白色正方形;
(2)某校计划按以上图案规律,用边长均为1米的白色正方形地砖和灰色正方形地砖铺设宽度为3米的走廊,若需要铺设的走廊长度为105米,则需要多少块白色地砖?
21.(2023·陕西西安·模拟预测)我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积为25,每个直角三角形两直角边的和为7,求中间小正方形的边长.
22.(23-24八年级上·安徽宿州·期末)某工厂去年的总产值比总支出多500万元,由于今年总产值比去年增加了15%,总支出比去年节约了10%,因此,今年总产值比总支出多950万元.
(1)设去年的总产值为x万元,总支出为y万元,请填写表:
总产值/万元 总支出/万元 差
去年 x y 500
今年
(2)求今年的总产值和总支出各多少万元?
23.(2023·浙江·一模)若规定符号的意义:.
(1)计算:_________.
(2)若,,则的值为________.
参考答案
1.B
A.,此选项错误,不符合题意;
B.,此选项正确,符合题意;
C.,此选项错误,不符合题意;
D.,此选项错误,不符合题意;
故选:B.
2.D
分别根据合并同类项、单项式除以单项式、同底数幂的乘法、幂的乘方法则进行计算即可求解.
解:A. 2a a=a,故原选项计算错误,不符合题意;
B. ,不是同类项不能合并,故原选项计算错误,不符合题意;
C. ,故原选项计算错误,不符合题意;
D. (-a3)2=a6,故原选项计算正确,符合题意.
3.C
解:A、不能计算,不符合题意;
B、,不是指数相乘,不符合题意;
C、,符合题意;
D、,不是指数相乘,不符合题意.
4.D
利用合并同类项,同底数幂相除,积的乘方,同底数幂相乘法则,逐项判断即可求解.
解:A、,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项错误,不符合题意;
D、,故本选项正确,符合题意;
5.B
解:①有两杯水,一杯的水温b是另一杯水温a的3倍低,则,
②土豆单价a比小米椒单价b的便宜2元,则,则,
③某文具店的装订机的价格b比文具盒的价格a的3倍少6元,则,
④有两根绳子,一根绳子的长度a比另一根绳子的长度b的3倍多6米,则,则,
综上所述:①③符合,
故选:B.
6.D
A.,原式计算错误,故选项不符合题意;
B.,原式计算错误,故选项不符合题意;
C.,原式计算错误,故选项不符合题意;
D.,原式计算正确,故选项符合题意.
故选:D.
7.A
解:
,
故选:A.
8.D
A. ,故选项错误,不符合题意;
B. ,故选项错误,不符合题意;
C. ,故选项错误,不符合题意;
D. ,故选项正确,符合题意;
故选:D
9.B
解:
得:,
∴,
∴,
∴,
∴,
故选:B.
10.A
先根据分式的混合运算化简,再整体代入即可作答.
,
∵,
∴原式,
故选:A.
11.A
解:∵点P(﹣1,)在“勾股一次函数”y=x+的图象上,
∴=﹣+,
∴a﹣b=﹣c,
又∵a,b,c分别是Rt△ABC的三条边长,∠C=90°,Rt△ABC的面积是4,
∴ab=4,即ab=8,
又∵a2+b2=c2,
∴(a﹣b)2+2ab=c2,
∴(﹣c)2+2×8=c2,
解得c=2,
故选:A
12.2
解:∵果与是同类项,
∴,
∴,
故答案为:2.
13.
解:∵,
∴,,
∴,,
∴;
故答案为:.
14.
解:原式
,
,
,
故原式.
15.91
解:2节链条的长度是(2.8×2-1),
3节链条的长度是(2.8×3-1×2),
n节链条的长度是2.8n-1×(n-1),
所以50节链条的长度是:2.8×50-1×(50-1)
=140-1×49
=91
故答案为:91
16.
,进而得到,计算即可得出结果.
解:令,
根据等式的基本性质2得:,
,
,
,
,
故答案为:.
17.
解:设原八角形边长为a,则图2正方形边长为2a+a、面积为(2a+a)2,四个小三角形面积和为2a2,
列式得(2a+a)2+2a2=8+4,
解得:a=1,
则AB=.
故答案为:
18.;
解:
当,时,
原式
.
19.(1)
(2)平方米
(1)解:阴影部分的面积
(2)解:当,,时,代入(1)得到的式子,
得(平方米).
答:阴影部分的面积为59600平方米
20.(1)23;
(2)263
(1)解:图1中有个白色正方形;
图2中有个白色正方形,
①图4中有个白色正方形;
②图n中有个白色正方形,
故答案为:①23;②;
(2)解:,
由(1)的规律得:,
答:需要263块白色地砖.
21.1
解:设直角三角形的两直角边中较长边为,较短边为,
大正方形的边长为,面积为,
由题意得:,
∴,
∴,
∴,
小正方形的边长为:.
22.(1),,950;
(2)今年的总产值为2300万元,总支出为1350万元.
(1)解:设去年总产值为x万元,总支出为y万元,
根据题意,得今年总产值为万元,今年总支出为万元,,今年总产值比总支出多950万元,
故答案为:,,950;
(2)解:根据题意,得,
解得:,
则,.
答:今年的总产值为2300万元,总支出为1350万元.
23.(1)5
(2)8或15
(1)根据题中的新定义得,
;
(2)∵,,
∴,
得,
∴或,
当时,,
当时.
∴的值为8或15.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
代数式重点考点 归纳练
2025年中考数学一轮复习备考
一、单选题
1.(2022·云南楚雄·一模)下列计算正确的是( )
A.(a-1)2=a2-1 B.4a·2a=8a2
C.2a-a=2 D.a8÷a2=a4
2.(2022·广西贵港·中考真题)下面计算正确的是( )
A. B. C. D.
3.(22-23八年级上·四川广安·期末)下列算式,能按照“底数不变,指数相乘”计算的是( )
A. B. C. D.
4.(2022·广西贺州·中考真题)下列运算正确的是( )
A. B. C. D.
5.(2024·福建福州·模拟预测)下面的四个问题中,都有a,b两个未知量:
①有两杯水,一杯的水温b是另一杯水温a的3倍低
②土豆单价a比小米椒单价b的便宜2元
③某文具店的装订机的价格b比文具盒的价格a的3倍少6元
④有两根绳子,一根绳子的长度a比另一根绳子的长度b的3倍多6米其中,未知量b可以用表示的是( )
A.①② B.①③ C.②③ D.②④
6.(2024·浙江绍兴·二模)下列计算正确的是( )
A. B. C. D.
7.(2024·天津河东·一模)计算的结果正确的是( )
A. B. C. D.
8.(2024·安徽六安·模拟预测)下列运算中,结果正确的是( )
A. B.
C. D.
9.(2024·广东汕头·一模)若关于x,y的方程组的解满足,则的值为( )
A.8 B. C.6 D.
10.(2023·山东济南·二模)若,则代数式的值为( )
A.2 B. C. D.
11.(2022·浙江宁波·一模)已知a,b,c分别是的三条边长,c为斜边长,,我们把关于x的形如的一次函数称为“勾股一次函数”,若点在“勾股一次函数”的图象上,且的面积是4,则c的值是( )
A. B.24 C. D.12
二、填空题
12.(22-23七年级上·陕西安康·期末)如果与是同类项,那么 .
13.(23-24八年级上·江苏淮安·期中)若x,y为实数, 且 ,则 .
14.(2024·四川成都·模拟预测)若,则代数式的值为 .
15.(2022·湖北十堰·中考真题)如图,某链条每节长为,每两节链条相连接部分重叠的圆的直径为,按这种连接方式,50节链条总长度为 .
16.(2023·福建莆田·一模)求的值,可以采用下面方法:
解:令
由等式的基本性质二得:
由平方差公式得:
令
请仿照上面的推理,计算出: .
17.(11-12九年级上·湖北黄冈·期末)如图1是一个八角星纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成如图3所示的大正方形,其面积为8+4,则图3中线段AB的长为 .
三、解答题
18.(22-23九年级下·广西南宁·阶段练习)先化简,再求值:,其中,.
19.(23-24七年级上·湖南郴州·期中)已知,如图,某长方形广场的四角都有一块边长为x米的正方形草地.若长方形的长为a米,宽为b米.
(1)请用代数式表示阴影部分的面积;
(2)若长方形广场的长为米,宽为米,正方形的边长为米,求阴影部分的面积.
20.(2023·安徽合肥·一模)观察下列由白色正方形和灰色正方形组成的图案,并解决问题.
(1)①图(4)中有 个白色正方形;②图(n)中有 (用含n的式子表示)个白色正方形;
(2)某校计划按以上图案规律,用边长均为1米的白色正方形地砖和灰色正方形地砖铺设宽度为3米的走廊,若需要铺设的走廊长度为105米,则需要多少块白色地砖?
21.(2023·陕西西安·模拟预测)我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积为25,每个直角三角形两直角边的和为7,求中间小正方形的边长.
22.(23-24八年级上·安徽宿州·期末)某工厂去年的总产值比总支出多500万元,由于今年总产值比去年增加了15%,总支出比去年节约了10%,因此,今年总产值比总支出多950万元.
(1)设去年的总产值为x万元,总支出为y万元,请填写表:
总产值/万元 总支出/万元 差
去年 x y 500
今年
(2)求今年的总产值和总支出各多少万元?
23.(2023·浙江·一模)若规定符号的意义:.
(1)计算:_________.
(2)若,,则的值为________.
参考答案
1.B
A.,此选项错误,不符合题意;
B.,此选项正确,符合题意;
C.,此选项错误,不符合题意;
D.,此选项错误,不符合题意;
故选:B.
2.D
分别根据合并同类项、单项式除以单项式、同底数幂的乘法、幂的乘方法则进行计算即可求解.
解:A. 2a a=a,故原选项计算错误,不符合题意;
B. ,不是同类项不能合并,故原选项计算错误,不符合题意;
C. ,故原选项计算错误,不符合题意;
D. (-a3)2=a6,故原选项计算正确,符合题意.
3.C
解:A、不能计算,不符合题意;
B、,不是指数相乘,不符合题意;
C、,符合题意;
D、,不是指数相乘,不符合题意.
4.D
利用合并同类项,同底数幂相除,积的乘方,同底数幂相乘法则,逐项判断即可求解.
解:A、,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项错误,不符合题意;
D、,故本选项正确,符合题意;
5.B
解:①有两杯水,一杯的水温b是另一杯水温a的3倍低,则,
②土豆单价a比小米椒单价b的便宜2元,则,则,
③某文具店的装订机的价格b比文具盒的价格a的3倍少6元,则,
④有两根绳子,一根绳子的长度a比另一根绳子的长度b的3倍多6米,则,则,
综上所述:①③符合,
故选:B.
6.D
A.,原式计算错误,故选项不符合题意;
B.,原式计算错误,故选项不符合题意;
C.,原式计算错误,故选项不符合题意;
D.,原式计算正确,故选项符合题意.
故选:D.
7.A
解:
,
故选:A.
8.D
A. ,故选项错误,不符合题意;
B. ,故选项错误,不符合题意;
C. ,故选项错误,不符合题意;
D. ,故选项正确,符合题意;
故选:D
9.B
解:
得:,
∴,
∴,
∴,
∴,
故选:B.
10.A
先根据分式的混合运算化简,再整体代入即可作答.
,
∵,
∴原式,
故选:A.
11.A
解:∵点P(﹣1,)在“勾股一次函数”y=x+的图象上,
∴=﹣+,
∴a﹣b=﹣c,
又∵a,b,c分别是Rt△ABC的三条边长,∠C=90°,Rt△ABC的面积是4,
∴ab=4,即ab=8,
又∵a2+b2=c2,
∴(a﹣b)2+2ab=c2,
∴(﹣c)2+2×8=c2,
解得c=2,
故选:A
12.2
解:∵果与是同类项,
∴,
∴,
故答案为:2.
13.
解:∵,
∴,,
∴,,
∴;
故答案为:.
14.
解:原式
,
,
,
故原式.
15.91
解:2节链条的长度是(2.8×2-1),
3节链条的长度是(2.8×3-1×2),
n节链条的长度是2.8n-1×(n-1),
所以50节链条的长度是:2.8×50-1×(50-1)
=140-1×49
=91
故答案为:91
16.
,进而得到,计算即可得出结果.
解:令,
根据等式的基本性质2得:,
,
,
,
,
故答案为:.
17.
解:设原八角形边长为a,则图2正方形边长为2a+a、面积为(2a+a)2,四个小三角形面积和为2a2,
列式得(2a+a)2+2a2=8+4,
解得:a=1,
则AB=.
故答案为:
18.;
解:
当,时,
原式
.
19.(1)
(2)平方米
(1)解:阴影部分的面积
(2)解:当,,时,代入(1)得到的式子,
得(平方米).
答:阴影部分的面积为59600平方米
20.(1)23;
(2)263
(1)解:图1中有个白色正方形;
图2中有个白色正方形,
①图4中有个白色正方形;
②图n中有个白色正方形,
故答案为:①23;②;
(2)解:,
由(1)的规律得:,
答:需要263块白色地砖.
21.1
解:设直角三角形的两直角边中较长边为,较短边为,
大正方形的边长为,面积为,
由题意得:,
∴,
∴,
∴,
小正方形的边长为:.
22.(1),,950;
(2)今年的总产值为2300万元,总支出为1350万元.
(1)解:设去年总产值为x万元,总支出为y万元,
根据题意,得今年总产值为万元,今年总支出为万元,,今年总产值比总支出多950万元,
故答案为:,,950;
(2)解:根据题意,得,
解得:,
则,.
答:今年的总产值为2300万元,总支出为1350万元.
23.(1)5
(2)8或15
(1)根据题中的新定义得,
;
(2)∵,,
∴,
得,
∴或,
当时,,
当时.
∴的值为8或15.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
