整式的乘除重点考点 归纳练 2025年中考数学一轮复习备考
文档属性
| 名称 | 整式的乘除重点考点 归纳练 2025年中考数学一轮复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 383.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-13 15:50:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
整式的乘除重点考点 归纳练
2025年中考数学一轮复习备考
一、单选题
1.(2024·江苏南通·二模)下列运算正确的是( )
A. B.
C. D.
2.(2022·山西临汾·二模)下列运算结果正确的是( )
A. B.
C. D.
3.(2022·浙江衢州·一模)下列运算正确的是( )
A.=﹣2 B.=±3
C.(a﹣3)2=a2﹣9 D.a2 a4=a8
4.(2023·内蒙古呼伦贝尔·一模)下列运算正确的是( )
A. B.
C. D.
5.(2022·海南海口·模拟预测)计算的结果正确的是( )
A. B. C. D.
6.(2024·江苏扬州·中考真题)下列运算中正确的是( )
A. B.
C. D.
7.(2021·江苏泰州·二模)下列运算正确的是( )
A.a+2a=3a2 B.(2ab)2=2ab2
C.a2 a3=a5 D.(a2)3=a5
8.(2024八年级·全国·竞赛)若,其中都是整数,则的值为( ).
A. B.4 C.6 D.8
9.(2023·四川内江·二模)下列运算正确的是( )
A. B.
C. D.
10.(2023·山东枣庄·一模)下列运算正确的是( )
A. B.
C. D.
11.(2023·四川巴中·中考真题)我国南宋时期数学家杨辉于1261年写下的《详解九章算法》,书中记载的图表给出了展开式的系数规律.
1
1 1
1 2 1
1 3 3 1
当代数式的值为1时,则x的值为( )
A.2 B. C.2或4 D.2或
12.(2024·江苏南通·一模)已知关于x的多项式,当时,该多项式的值为,则多项式的值可以是( )
A. B.2 C. D.
二、填空题
13.(22-23七年级上·江苏·阶段练习)计算: .
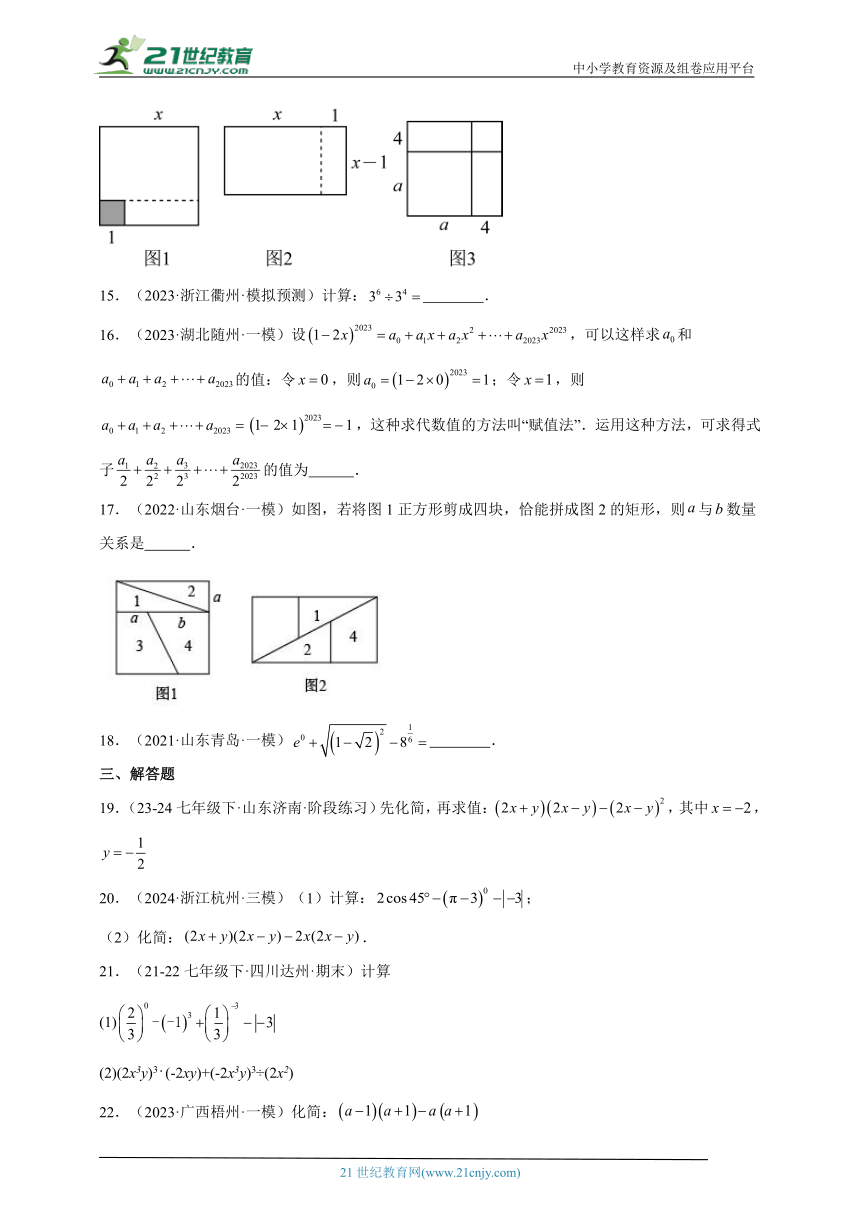
14.(2023·河北沧州·模拟预测)如图1,将边长为的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.利用图形1、2的面积,用因式分解的方法表示一个恒等式为 ;利用图3的面积,用整式的乘法的形式表示一个恒等式 .
15.(2023·浙江衢州·模拟预测)计算: .
16.(2023·湖北随州·一模)设,可以这样求和的值:令,则;令,则,这种求代数值的方法叫“赋值法”.运用这种方法,可求得式子的值为 .
17.(2022·山东烟台·一模)如图,若将图1正方形剪成四块,恰能拼成图2的矩形,则与数量关系是 .
18.(2021·山东青岛·一模) .
三、解答题
19.(23-24七年级下·山东济南·阶段练习)先化简,再求值:,其中,
20.(2024·浙江杭州·三模)(1)计算:;
(2)化简:.
21.(21-22七年级下·四川达州·期末)计算
(1)
(2)(2x3y)3(-2xy)+(-2x3y)3÷(2x2)
22.(2023·广西梧州·一模)化简:
23.(2022·湖北十堰·三模)计算:.
24.(2024·辽宁沈阳·模拟预测)(1)计算:
(2)解方程:
参考答案
1.D
解:A. ,故此选项错误;
B. ,故此选项错误;
C. ,故此选项错误;
D. ,故此选项正确
故选:D
2.C
根据整式的运算法则即可判断.
解:,故A错误;
,故B错误;
,故C正确;
,故D错误;
故选:C.
3.A
根据立方根和算术平方根的定义,完全平方公式,同底数幂的乘法逐项计算,即可判断.
,故A计算正确,符合题意;
,故B计算错误,不符合题意;
,故C计算错误,不符合题意;
,故D计算错误,不符合题意.
4.C
解:A、,故A不符合题意;
B、,故B不符合题意;
C、,故C符合题意;
D、,故D不符合题意;
故选:C.
5.B
解:
故选:B.
6.B
解:A、,原选项错误,不符合题意;
B、,正确,符合题意;
C、,原选项错误,不符合题意;
D、,原选项错误,不符合题意;
故选:B .
7.C
解:A、a+2a=3a,故本选项不符合题意;
B、(2ab)2=4a2b2,故本选项不符合题意;
C、a2 a3=a5,故本选项符合题意;
D、(a2)3=a6,故本选项不符合题意;
故选:C.
8.A
解:∵,
∴,
∴,
∴,
解得: ,
∴.
故选:A.
9.C
解:A. ,故此选项错误,不符合题意;
B. ,故此选项错误,不符合题意;
C. ,故此选项正确,符合题意;
D. ,故此选项错误,不符合题意;
10.D
解:A., 原选项计算错误,故A不符合题意;
B. , 原选项计算错误,故B不符合题意;
C. , 原选项计算错误,故C不符合题意;
D. ,计算正确,故D符合题意,
11.C
解:由规律可得:,
令,,
∴,
∵,
∴,
∴,
∴或,
12.A
当时,该多项式的值为,
,
整理得,
,
,
即,
,
,,
,
,
当时,,
根据二次函数的图象可知,当时,.
故选A.
13.-1
解:原式=
=
=-1
故答案为:-1.
14.
解:由图1、2可得,图1的面积为:,
图2的面积为:,
∴,
由图4可得,,
故答案为:;;
15.9
解:
.
故答案为:9.
16.
解:令,则,
令,则,
∴令,则,
∵,
∴,
∴,
故答案为:.
17.
解:依题意得(a+b)2=b(b+a+b),
整理得:a2+b2+2ab=2b2+ab,
则a2-b2+ab=0,
方程两边同时除以b2,
则,
解得:,
∵不能为负,
∴,
∴,
故答案为:.
18.0
解:
故答案为:0.
19.,
解:原式
将, 代入
原式
20.(1);(2)
解:(1)
;
(2)
21.(1)26
(2)
(1)根据零次幂、负指数幂可进行求解;
(2)根据积的乘方、单项式的乘除法可进行求解.
(1)解:原式=;
(2)解:原式=
=.
22.
先用平方差公式和单项式乘多项式的运算法则进行计算,再合并同类项即可.
解:原式
23.
根据乘方、负整数指数幂,绝对值的意义计算即可.
解:原式
.
24.(1);(2),
解:(1)原式
.
(2)移项,得.
配方,得,即.
.
,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
整式的乘除重点考点 归纳练
2025年中考数学一轮复习备考
一、单选题
1.(2024·江苏南通·二模)下列运算正确的是( )
A. B.
C. D.
2.(2022·山西临汾·二模)下列运算结果正确的是( )
A. B.
C. D.
3.(2022·浙江衢州·一模)下列运算正确的是( )
A.=﹣2 B.=±3
C.(a﹣3)2=a2﹣9 D.a2 a4=a8
4.(2023·内蒙古呼伦贝尔·一模)下列运算正确的是( )
A. B.
C. D.
5.(2022·海南海口·模拟预测)计算的结果正确的是( )
A. B. C. D.
6.(2024·江苏扬州·中考真题)下列运算中正确的是( )
A. B.
C. D.
7.(2021·江苏泰州·二模)下列运算正确的是( )
A.a+2a=3a2 B.(2ab)2=2ab2
C.a2 a3=a5 D.(a2)3=a5
8.(2024八年级·全国·竞赛)若,其中都是整数,则的值为( ).
A. B.4 C.6 D.8
9.(2023·四川内江·二模)下列运算正确的是( )
A. B.
C. D.
10.(2023·山东枣庄·一模)下列运算正确的是( )
A. B.
C. D.
11.(2023·四川巴中·中考真题)我国南宋时期数学家杨辉于1261年写下的《详解九章算法》,书中记载的图表给出了展开式的系数规律.
1
1 1
1 2 1
1 3 3 1
当代数式的值为1时,则x的值为( )
A.2 B. C.2或4 D.2或
12.(2024·江苏南通·一模)已知关于x的多项式,当时,该多项式的值为,则多项式的值可以是( )
A. B.2 C. D.
二、填空题
13.(22-23七年级上·江苏·阶段练习)计算: .
14.(2023·河北沧州·模拟预测)如图1,将边长为的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.利用图形1、2的面积,用因式分解的方法表示一个恒等式为 ;利用图3的面积,用整式的乘法的形式表示一个恒等式 .
15.(2023·浙江衢州·模拟预测)计算: .
16.(2023·湖北随州·一模)设,可以这样求和的值:令,则;令,则,这种求代数值的方法叫“赋值法”.运用这种方法,可求得式子的值为 .
17.(2022·山东烟台·一模)如图,若将图1正方形剪成四块,恰能拼成图2的矩形,则与数量关系是 .
18.(2021·山东青岛·一模) .
三、解答题
19.(23-24七年级下·山东济南·阶段练习)先化简,再求值:,其中,
20.(2024·浙江杭州·三模)(1)计算:;
(2)化简:.
21.(21-22七年级下·四川达州·期末)计算
(1)
(2)(2x3y)3(-2xy)+(-2x3y)3÷(2x2)
22.(2023·广西梧州·一模)化简:
23.(2022·湖北十堰·三模)计算:.
24.(2024·辽宁沈阳·模拟预测)(1)计算:
(2)解方程:
参考答案
1.D
解:A. ,故此选项错误;
B. ,故此选项错误;
C. ,故此选项错误;
D. ,故此选项正确
故选:D
2.C
根据整式的运算法则即可判断.
解:,故A错误;
,故B错误;
,故C正确;
,故D错误;
故选:C.
3.A
根据立方根和算术平方根的定义,完全平方公式,同底数幂的乘法逐项计算,即可判断.
,故A计算正确,符合题意;
,故B计算错误,不符合题意;
,故C计算错误,不符合题意;
,故D计算错误,不符合题意.
4.C
解:A、,故A不符合题意;
B、,故B不符合题意;
C、,故C符合题意;
D、,故D不符合题意;
故选:C.
5.B
解:
故选:B.
6.B
解:A、,原选项错误,不符合题意;
B、,正确,符合题意;
C、,原选项错误,不符合题意;
D、,原选项错误,不符合题意;
故选:B .
7.C
解:A、a+2a=3a,故本选项不符合题意;
B、(2ab)2=4a2b2,故本选项不符合题意;
C、a2 a3=a5,故本选项符合题意;
D、(a2)3=a6,故本选项不符合题意;
故选:C.
8.A
解:∵,
∴,
∴,
∴,
解得: ,
∴.
故选:A.
9.C
解:A. ,故此选项错误,不符合题意;
B. ,故此选项错误,不符合题意;
C. ,故此选项正确,符合题意;
D. ,故此选项错误,不符合题意;
10.D
解:A., 原选项计算错误,故A不符合题意;
B. , 原选项计算错误,故B不符合题意;
C. , 原选项计算错误,故C不符合题意;
D. ,计算正确,故D符合题意,
11.C
解:由规律可得:,
令,,
∴,
∵,
∴,
∴,
∴或,
12.A
当时,该多项式的值为,
,
整理得,
,
,
即,
,
,,
,
,
当时,,
根据二次函数的图象可知,当时,.
故选A.
13.-1
解:原式=
=
=-1
故答案为:-1.
14.
解:由图1、2可得,图1的面积为:,
图2的面积为:,
∴,
由图4可得,,
故答案为:;;
15.9
解:
.
故答案为:9.
16.
解:令,则,
令,则,
∴令,则,
∵,
∴,
∴,
故答案为:.
17.
解:依题意得(a+b)2=b(b+a+b),
整理得:a2+b2+2ab=2b2+ab,
则a2-b2+ab=0,
方程两边同时除以b2,
则,
解得:,
∵不能为负,
∴,
∴,
故答案为:.
18.0
解:
故答案为:0.
19.,
解:原式
将, 代入
原式
20.(1);(2)
解:(1)
;
(2)
21.(1)26
(2)
(1)根据零次幂、负指数幂可进行求解;
(2)根据积的乘方、单项式的乘除法可进行求解.
(1)解:原式=;
(2)解:原式=
=.
22.
先用平方差公式和单项式乘多项式的运算法则进行计算,再合并同类项即可.
解:原式
23.
根据乘方、负整数指数幂,绝对值的意义计算即可.
解:原式
.
24.(1);(2),
解:(1)原式
.
(2)移项,得.
配方,得,即.
.
,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
