7.2.2平行线的判定 学案(无答案)2024-2025人教版2024七年级下册
文档属性
| 名称 | 7.2.2平行线的判定 学案(无答案)2024-2025人教版2024七年级下册 |  | |
| 格式 | doc | ||
| 文件大小 | 1002.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 13:05:28 | ||
图片预览

文档简介
7.2.2平行线的判定 学案
一、学习目标
1.掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行.
2.经历平行线判定方法的探究过程,从中体会转化的数学思想.
3.能够根据平行线的判定方法进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
重点:掌握平行线的三种判定方法.
难点:会利用平行线的判定方法进行简单推理.
二、学习过程
(一)情境引入
问题1 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
问题2 通过学习一条直线与另一条直线相交,一条直线分别与两条直线相交的知识,同学们都认识了哪些角呢?
(二)合作探究
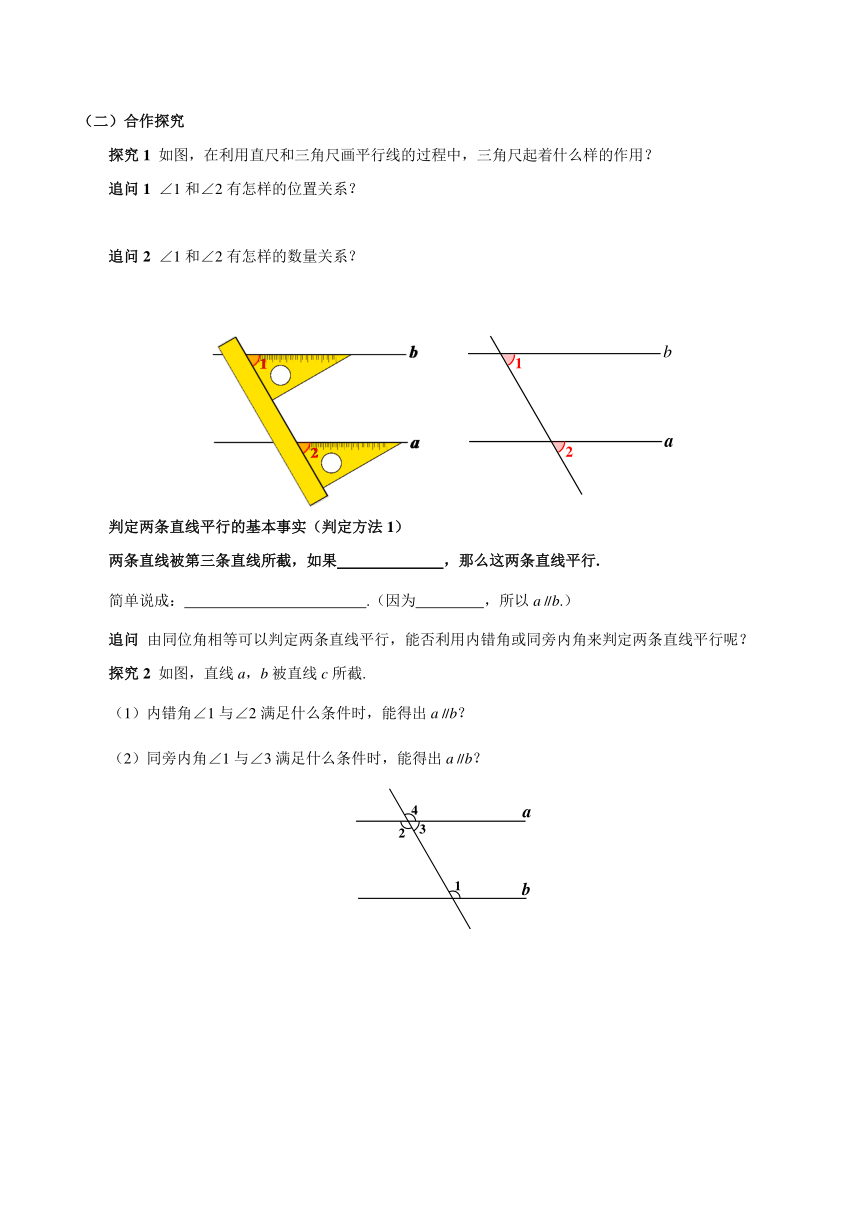
探究1 如图,在利用直尺和三角尺画平行线的过程中,三角尺起着什么样的作用?
追问1 ∠1和∠2有怎样的位置关系?
追问2 ∠1和∠2有怎样的数量关系?
判定两条直线平行的基本事实(判定方法1)
两条直线被第三条直线所截,如果 ,那么这两条直线平行.
简单说成: .(因为 ,所以a∥b.)
追问 由同位角相等可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
探究2 如图,直线a,b被直线c所截.
内错角∠1与∠2满足什么条件时,能得出a∥b?
同旁内角∠1与∠3满足什么条件时,能得出a∥b?
判定方法2
两条直线被第三条直线所截,如果 ,那么这两条直线平行.
简单说成: .(因为 ,所以a∥b.)
判定方法3
两条直线被第三条直线所截,如果 ,那么这两条直线平行.
简单说成: .(因为 ,所以a∥b.)
遇到一个新问题时,常常把它 为已知的(或已解决的)问题.
问题解决 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
(三)典例分析
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
转化1 自然语言→符号语言
转化2 平行线→ →垂直
追问 你还有其他转化方法吗?
转化1 平行线→ →垂直
转化2 平行线→ →垂直
转化3 符号语言→自然语言
追问 “在同一平面内”可以省略吗?为什么?
(四)巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(1)如果∠B=∠DCG,那么可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,那么可以判断哪两条直线平行?为什么?
(3)如果∠D+∠DFE=180°,那么可以判断哪两条直线平行?为什么?
2. 如图,木工常用角尺画平行线,你能说出其中的道理吗?
3. 如图,在下列条件中,能判断直线a∥b的是( )
A.∠2+∠5=180° B.∠2=∠4 C.∠4+∠5=180° D.∠1=∠3
第2题图 第3题图 第4题图
4. 在铺设钢轨时,两条钢轨必须是互相平行的.如图,已知∠2是直角,要判断两条钢轨是否平行,只需要再度量图中标出的哪个角,为什么?
5. 如左图是两条道路互相垂直的交叉路口,你能画出它的平面示意图(用两条平行线段表示一条道路)吗?你能用类似的方法,画出右图的平面示意图吗?你能画出两条道路呈45°角的交叉路口的平面示意图吗?
示意图1 示意图2 示意图3
归纳总结
一、学习目标
1.掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行.
2.经历平行线判定方法的探究过程,从中体会转化的数学思想.
3.能够根据平行线的判定方法进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
重点:掌握平行线的三种判定方法.
难点:会利用平行线的判定方法进行简单推理.
二、学习过程
(一)情境引入
问题1 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
问题2 通过学习一条直线与另一条直线相交,一条直线分别与两条直线相交的知识,同学们都认识了哪些角呢?
(二)合作探究
探究1 如图,在利用直尺和三角尺画平行线的过程中,三角尺起着什么样的作用?
追问1 ∠1和∠2有怎样的位置关系?
追问2 ∠1和∠2有怎样的数量关系?
判定两条直线平行的基本事实(判定方法1)
两条直线被第三条直线所截,如果 ,那么这两条直线平行.
简单说成: .(因为 ,所以a∥b.)
追问 由同位角相等可以判定两条直线平行,能否利用内错角或同旁内角来判定两条直线平行呢?
探究2 如图,直线a,b被直线c所截.
内错角∠1与∠2满足什么条件时,能得出a∥b?
同旁内角∠1与∠3满足什么条件时,能得出a∥b?
判定方法2
两条直线被第三条直线所截,如果 ,那么这两条直线平行.
简单说成: .(因为 ,所以a∥b.)
判定方法3
两条直线被第三条直线所截,如果 ,那么这两条直线平行.
简单说成: .(因为 ,所以a∥b.)
遇到一个新问题时,常常把它 为已知的(或已解决的)问题.
问题解决 如图,有一块长方形玻璃,如何检验它相对的两条边是否平行?
(三)典例分析
例1 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
转化1 自然语言→符号语言
转化2 平行线→ →垂直
追问 你还有其他转化方法吗?
转化1 平行线→ →垂直
转化2 平行线→ →垂直
转化3 符号语言→自然语言
追问 “在同一平面内”可以省略吗?为什么?
(四)巩固练习
1. 如图,E是AB上一点,F是DC上一点,G是BC的延长线上一点.
(1)如果∠B=∠DCG,那么可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,那么可以判断哪两条直线平行?为什么?
(3)如果∠D+∠DFE=180°,那么可以判断哪两条直线平行?为什么?
2. 如图,木工常用角尺画平行线,你能说出其中的道理吗?
3. 如图,在下列条件中,能判断直线a∥b的是( )
A.∠2+∠5=180° B.∠2=∠4 C.∠4+∠5=180° D.∠1=∠3
第2题图 第3题图 第4题图
4. 在铺设钢轨时,两条钢轨必须是互相平行的.如图,已知∠2是直角,要判断两条钢轨是否平行,只需要再度量图中标出的哪个角,为什么?
5. 如左图是两条道路互相垂直的交叉路口,你能画出它的平面示意图(用两条平行线段表示一条道路)吗?你能用类似的方法,画出右图的平面示意图吗?你能画出两条道路呈45°角的交叉路口的平面示意图吗?
示意图1 示意图2 示意图3
归纳总结
同课章节目录
