第二十六章 反比例函数 单元试卷(含答案)2024-2025学年人教版九年级下册
文档属性
| 名称 | 第二十六章 反比例函数 单元试卷(含答案)2024-2025学年人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 337.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 00:00:00 | ||
图片预览




文档简介
第二十六章 反比例函数 单元试卷
一、选择题
下列函数中, 与 之间是反比例函数关系的是
A. B. C. D.
如果反比例函数 的图象经过点 ,那么函数的图象应在
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
关于反比例函数 ,下列说法不正确的是
A.点 在它的图象上
B.它的图象在第一、三象限
C. 的值随着 的值的增大而减小
D.它的图象关于原点中心对称
若反比例函数 的图象位于第一、第三象限,则 的取值可以是
A. B. C. D.
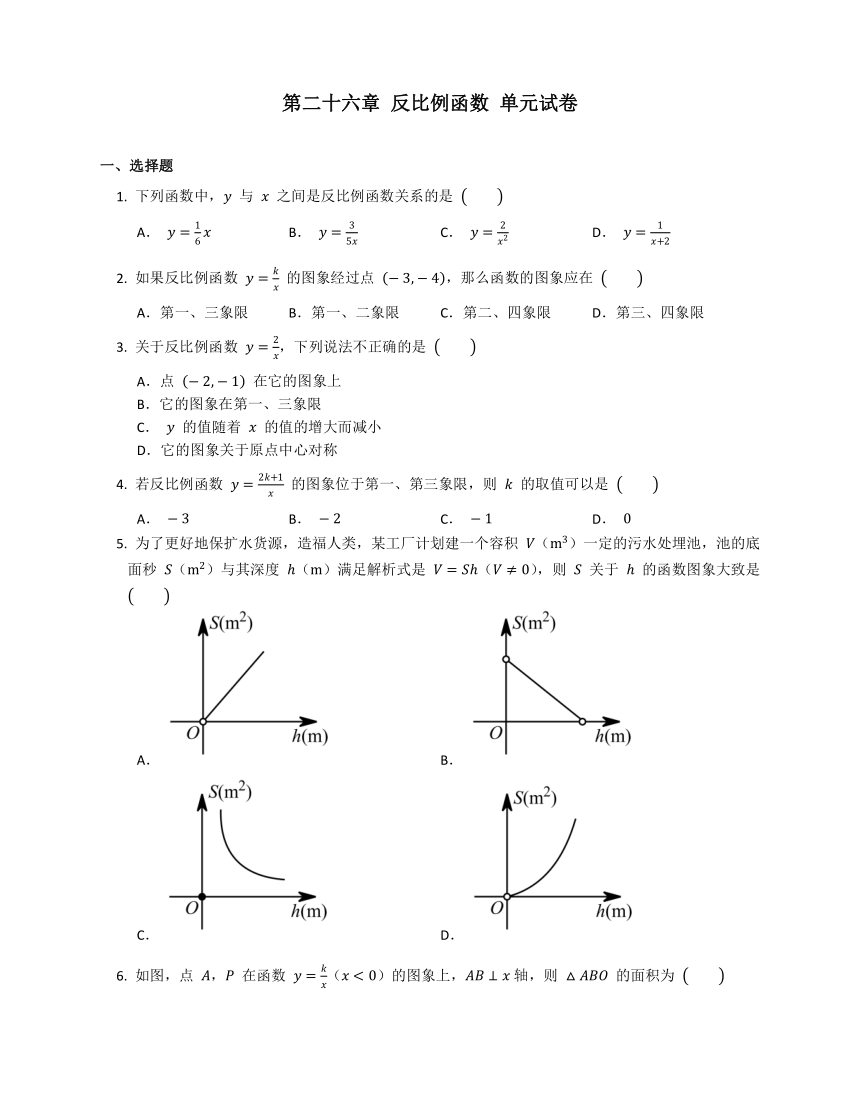
为了更好地保扩水货源,造福人类,某工厂计划建一个容积 ()一定的污水处埋池,池的底面秒 ()与其深度 ()满足解析式是 (),则 关于 的函数图象大致是
A. B.
C. D.
如图,点 , 在函数 ()的图象上,,则 的面积为
A. B. C. D.
在平面直角坐标系中,反比例函数 的图象上有三点 ,,.若 且 ,则 的取值范围为
A. B. 或
C. D. 或
如图,正方形 的顶点 , 在 轴的正半轴上,反比例函数 ()在第一象限的图象经过顶点 和 边上的点 ,连接 ,,,则 的面积为
A. B. C. D.
二、填空题
反比例函数 的图象一定经过点(, ).
有下列函数:① ;② ;③ ;④ ;⑤ ;⑥ .其中 随 的增大而增大的是 (填序号).
已知某省的陆地面积为 ,人均占有的陆地面积 ()随全省人口数 的变化而变化,其关系可用函数表达式表示为 .
已知反比例函数 的图象与一次函数 的图象相交于点 ,则 .
已知关于 的一次函数 和反比例函数 的图象都经过点 ,则 , .
若 与 成反比例, 与 成正比例,则 是 的 函数.
观察函数 的图象,当 时, ;当 时, 的取值范围是 ;当 时, 的取值范围是 .
三、解答题
如图所示,一次函数 的图象与反比例函数 的图象交于 , 两点.
(1) 求反比例函数和一次函数的表达式;
(2) 求使一次函数的值大于反比例函数的值时 的取值范围.
已知蓄电池的电压为定值.使用此蓄电池作为电源时,电流 (单位:)与电阻 (单位:)是反比例函数关系,它的图象如图所示.
(1) 求这个反比例函数的表达式;
(2) 如果以此蓄电池为电源的用电器的电流不能超过 ,那么该用电器的可变电阻至少是多少?
如图,在平面直角坐标系中,已知点 ,.反比例函数 的图象经过点 ,直线 与反比例函数的图象交于点 ,与直线 交于点 .
(1) 求 的值.
(2) 求 的面积.
已知:如图,平面直角坐标系中有一个等腰梯形 ,且 ,,点 在 轴正半轴上,点 , 在 轴上(点 在点 的左侧),点 在第一象限,,,梯形的高为 ,双曲线 经过点 ,直线 经过 , 两点.
(1) 求点 ,,, 的坐标;
(2) 求双曲线 和直线 的解析式;
(3) 点 在双曲线上,点 在 轴上,如果四边形 是平行四边形,求点 的坐标.
为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量 (毫克/立方米)与药物点燃后的时间 (分钟)成正比例,药物燃尽后, 与 成反比例(如图所示).已知药物点燃后 分钟燃尽,此时室内每立方米空气中含药量为 毫克.
(1) 求药物然烧时, 与 之间函数的表达式.
(2) 求药物燃尽后, 与 之间函数的表达式.
(3) 研究表明,当空气中每立方米的含药量不低于 毫克,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长.
如图,矩形 的两边 , 的长分别为 ,,且 , 在 轴的负半轴上, 是 的中点,反比例函数 的图象经过点 ,与 交于点 .
(1) 若点 坐标为 ,求 的值.
(2) 若 ,且点 的横坐标为 ,则点 的横坐标为 (用含 的代数式表示),点 的纵坐标为 ,反比例函数的表达式为 .
答案
一、选择题
1. B
2. A
3. C
4. D
5. C
6. A
7. D
8. B
二、填空题
9.
10. ②⑥
11.
12.
13. ;
14. 反比例
15. ; 或 ; 或
三、解答题
16.
(1) 把 代入 得:,
反比例函数的解析式是 .
代入反比例函数 得:,
的坐标是 .
把 , 的坐标代入一次函数 得
解得:
一次函数的解析式是 .
(2) 当 或 时,一次函数的值大于反比例函数的值.
17.
(1) 设反比例函数表达式为 ,
将 代入得 ,,
反比例函数表达式为 .
(2) 对于 ,当 时,,
由图象可知, 随着 的增大而减小,
当 时,.
答:用电器可变电阻至少 .
18.
(1) 反比例函数 的图象经过点 ,
,解得 .
(2) 设直线 的解析式为 ,
把点 , 代入得 解得
直线 的解析式为 ,
则 ,,
,
.
19.
(1) 过点 作 轴于点 .
四边形 是矩形,
,,,
在 和 中,
().
,
梯形的高为 ,
.
,,
,.
,,,.
(2) 双曲线 经过点 ,
.
双曲线的解析式为:,
直线 经过 , 两点,
得:
解得:
直线的解析式为:.
(3) 四边形 是平行四边形.
且 .
点 在 轴上,
过点 作 轴的垂线与双曲线 的交点即为点 .
点 的坐标为 ,
.
,
,
点 的坐标为 .
20.
(1) 药物燃烧时,设 ,
将
代入得,,
解得 ,
则 .
(2) 药物燃烧尽后,设 ,
将 带入得,
,解得 ,
则 .
(3) 在 中,当 时,
解得 ,
在 中,当 时,
,解得 ,
则此次消毒有效时间为 (分钟).
21.
(1) , 的长分别为 ,, 是 的中点,
,,
又 是 的中点,点 坐标为 ,
,,
,
又 反比例函数 的图象经过点 ,
.
(2) ;;
一、选择题
下列函数中, 与 之间是反比例函数关系的是
A. B. C. D.
如果反比例函数 的图象经过点 ,那么函数的图象应在
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
关于反比例函数 ,下列说法不正确的是
A.点 在它的图象上
B.它的图象在第一、三象限
C. 的值随着 的值的增大而减小
D.它的图象关于原点中心对称
若反比例函数 的图象位于第一、第三象限,则 的取值可以是
A. B. C. D.
为了更好地保扩水货源,造福人类,某工厂计划建一个容积 ()一定的污水处埋池,池的底面秒 ()与其深度 ()满足解析式是 (),则 关于 的函数图象大致是
A. B.
C. D.
如图,点 , 在函数 ()的图象上,,则 的面积为
A. B. C. D.
在平面直角坐标系中,反比例函数 的图象上有三点 ,,.若 且 ,则 的取值范围为
A. B. 或
C. D. 或
如图,正方形 的顶点 , 在 轴的正半轴上,反比例函数 ()在第一象限的图象经过顶点 和 边上的点 ,连接 ,,,则 的面积为
A. B. C. D.
二、填空题
反比例函数 的图象一定经过点(, ).
有下列函数:① ;② ;③ ;④ ;⑤ ;⑥ .其中 随 的增大而增大的是 (填序号).
已知某省的陆地面积为 ,人均占有的陆地面积 ()随全省人口数 的变化而变化,其关系可用函数表达式表示为 .
已知反比例函数 的图象与一次函数 的图象相交于点 ,则 .
已知关于 的一次函数 和反比例函数 的图象都经过点 ,则 , .
若 与 成反比例, 与 成正比例,则 是 的 函数.
观察函数 的图象,当 时, ;当 时, 的取值范围是 ;当 时, 的取值范围是 .
三、解答题
如图所示,一次函数 的图象与反比例函数 的图象交于 , 两点.
(1) 求反比例函数和一次函数的表达式;
(2) 求使一次函数的值大于反比例函数的值时 的取值范围.
已知蓄电池的电压为定值.使用此蓄电池作为电源时,电流 (单位:)与电阻 (单位:)是反比例函数关系,它的图象如图所示.
(1) 求这个反比例函数的表达式;
(2) 如果以此蓄电池为电源的用电器的电流不能超过 ,那么该用电器的可变电阻至少是多少?
如图,在平面直角坐标系中,已知点 ,.反比例函数 的图象经过点 ,直线 与反比例函数的图象交于点 ,与直线 交于点 .
(1) 求 的值.
(2) 求 的面积.
已知:如图,平面直角坐标系中有一个等腰梯形 ,且 ,,点 在 轴正半轴上,点 , 在 轴上(点 在点 的左侧),点 在第一象限,,,梯形的高为 ,双曲线 经过点 ,直线 经过 , 两点.
(1) 求点 ,,, 的坐标;
(2) 求双曲线 和直线 的解析式;
(3) 点 在双曲线上,点 在 轴上,如果四边形 是平行四边形,求点 的坐标.
为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量 (毫克/立方米)与药物点燃后的时间 (分钟)成正比例,药物燃尽后, 与 成反比例(如图所示).已知药物点燃后 分钟燃尽,此时室内每立方米空气中含药量为 毫克.
(1) 求药物然烧时, 与 之间函数的表达式.
(2) 求药物燃尽后, 与 之间函数的表达式.
(3) 研究表明,当空气中每立方米的含药量不低于 毫克,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长.
如图,矩形 的两边 , 的长分别为 ,,且 , 在 轴的负半轴上, 是 的中点,反比例函数 的图象经过点 ,与 交于点 .
(1) 若点 坐标为 ,求 的值.
(2) 若 ,且点 的横坐标为 ,则点 的横坐标为 (用含 的代数式表示),点 的纵坐标为 ,反比例函数的表达式为 .
答案
一、选择题
1. B
2. A
3. C
4. D
5. C
6. A
7. D
8. B
二、填空题
9.
10. ②⑥
11.
12.
13. ;
14. 反比例
15. ; 或 ; 或
三、解答题
16.
(1) 把 代入 得:,
反比例函数的解析式是 .
代入反比例函数 得:,
的坐标是 .
把 , 的坐标代入一次函数 得
解得:
一次函数的解析式是 .
(2) 当 或 时,一次函数的值大于反比例函数的值.
17.
(1) 设反比例函数表达式为 ,
将 代入得 ,,
反比例函数表达式为 .
(2) 对于 ,当 时,,
由图象可知, 随着 的增大而减小,
当 时,.
答:用电器可变电阻至少 .
18.
(1) 反比例函数 的图象经过点 ,
,解得 .
(2) 设直线 的解析式为 ,
把点 , 代入得 解得
直线 的解析式为 ,
则 ,,
,
.
19.
(1) 过点 作 轴于点 .
四边形 是矩形,
,,,
在 和 中,
().
,
梯形的高为 ,
.
,,
,.
,,,.
(2) 双曲线 经过点 ,
.
双曲线的解析式为:,
直线 经过 , 两点,
得:
解得:
直线的解析式为:.
(3) 四边形 是平行四边形.
且 .
点 在 轴上,
过点 作 轴的垂线与双曲线 的交点即为点 .
点 的坐标为 ,
.
,
,
点 的坐标为 .
20.
(1) 药物燃烧时,设 ,
将
代入得,,
解得 ,
则 .
(2) 药物燃烧尽后,设 ,
将 带入得,
,解得 ,
则 .
(3) 在 中,当 时,
解得 ,
在 中,当 时,
,解得 ,
则此次消毒有效时间为 (分钟).
21.
(1) , 的长分别为 ,, 是 的中点,
,,
又 是 的中点,点 坐标为 ,
,,
,
又 反比例函数 的图象经过点 ,
.
(2) ;;
