16.3《二次根式的混合运算》课件(共26张PPT)人教版数学八年级下册
文档属性
| 名称 | 16.3《二次根式的混合运算》课件(共26张PPT)人教版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 570.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 20:47:10 | ||
图片预览






文档简介
(共26张PPT)
二次根式的加减(二)
人教版 数学 八年级 下册
二次根式的混合运算
学习目标
(1)类比整式运算法则,探索二次根式的加、减、乘、除混合运算顺序的步骤和方法.
(2)能熟练地进行二次根式的加、减、乘、除混合运算.
(3)通过学习二次根式的加、减、乘、除混合运算的学习,培养运算能力、推理能力和应用意识.
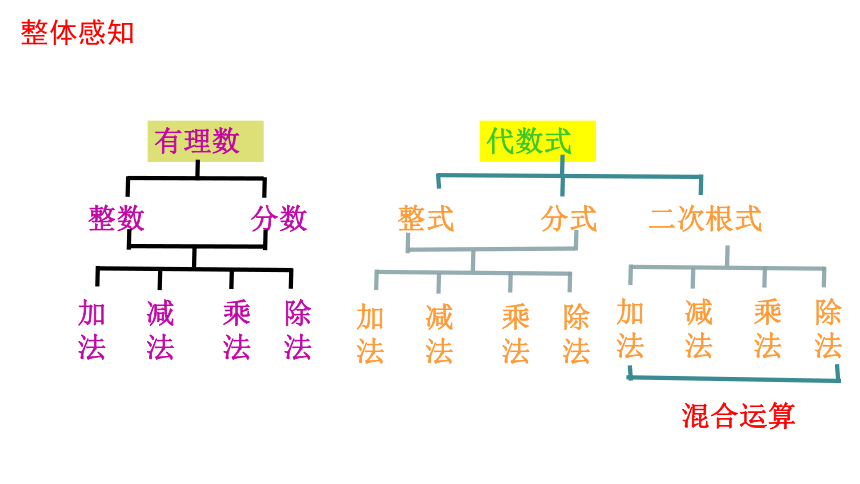
有理数
代数式
整数
分数
加 减 乘 除
法 法 法 法
整式
分式
二次根式
加 减 乘 除
法 法 法 法
加 减 乘 除
法 法 法 法
整体感知
混合运算
复习导入
1.单项式与多项式、多项式与多项式的乘法法则法则分别是什么
3.整式乘法运算中的乘法公式有哪些
2.多项式与单项式的除法法则是什么
m(a+b+c)=ma+mb+mc
(m+n)(a+b)=ma+mb+na+nb
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
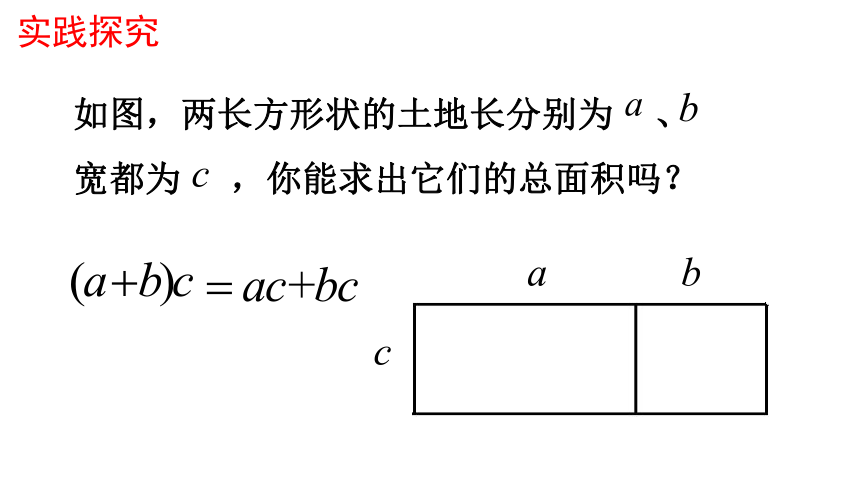
实践探究
如图,两长方形状的土地长分别为 、
宽都为 ,你能求出它们的总面积吗?
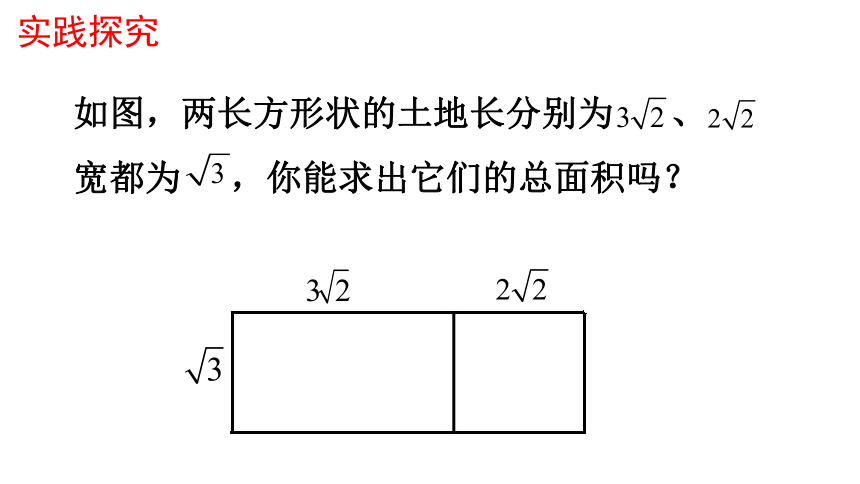
如图,两长方形状的土地长分别为 、
宽都为 ,你能求出它们的总面积吗?
实践探究
思考:从上面的运算结果、运算律能发现了什么?
这两种方法的结果是相同的.可见,单项式乘以多项式(乘法分配律)在二次根式计算中依然适用.
实践探究
实践探究
实际问题:
如图,长方形状的土地长分别为 、
宽都分别为 、 ,你能求出它们的总面积吗?
实践探究
如图,两长方形状的土地长分别为 、
宽都分别为 、 ,你能求出它们的总面积吗?
解:原式
a
b
a
b
b
实践探究
如图,两正方形边长分别为 、 ,你能求出
阴影面积吗?
解原式
实践探究
如图,两正方形边长分别为 、 ,你能求出
阴影面积吗?
实践探究
如图,两正方形边长分别为 、 ,你能求出
所有图形的总面积吗?
解:原式
探究活动4
如图,两正方形边长分别为 、 ,你能求出
所有图形的总面积吗?
思考:
如果整式所有的运算法则中的字母改写成二次根式,是否仍成立呢?为什么?
整式运算中的字母,它的意义十分广泛,可以代表所有一切,当然也可以代表二次根式,所以,整式中的运算法则、运算律也适用于二次根式.
积极思考
思考: 应先计算什么呢?依据是什么?
动手动脑
思考: 应先计算什么呢? 依据是什么?
知识运用
(1) (2)
(3) (4)
知识运用
知识运用
解:
当堂练习
1.下列计算正确的是( )
A.
B.
C.
D.
B
2.已知 , 则 的值为( )
A. 2 B. 4 C. 5 D.7
B
3.计算:
5
4.设 则a b.(填“>”“ < ”或 “= ”)
=
谈谈我们今天的收获和困惑?
回顾反思
通过本节的学习,你认为二次根式运算时应关注哪些方面?通常用到哪些知识?
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a + b)(a - b) = a2 - b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(x + a)(x + b) = x2+(a+b)x+ ab
运算顺序,先算乘方,再算乘除,再算加减,有括号,先算括号里的
课后作业
巩固作业:课本15页习题第4题
拓展作业:1.若,则代数式
2.计算(1)
探究作业:
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式1 = .
变式2 已知 , ,求 的值
变式3 求
探究作业
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式1 = .
解:原式
思维延伸
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式2 已知 , ,求 的值.
思维延伸
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式3 求
思维延伸
二次根式的加减(二)
人教版 数学 八年级 下册
二次根式的混合运算
学习目标
(1)类比整式运算法则,探索二次根式的加、减、乘、除混合运算顺序的步骤和方法.
(2)能熟练地进行二次根式的加、减、乘、除混合运算.
(3)通过学习二次根式的加、减、乘、除混合运算的学习,培养运算能力、推理能力和应用意识.
有理数
代数式
整数
分数
加 减 乘 除
法 法 法 法
整式
分式
二次根式
加 减 乘 除
法 法 法 法
加 减 乘 除
法 法 法 法
整体感知
混合运算
复习导入
1.单项式与多项式、多项式与多项式的乘法法则法则分别是什么
3.整式乘法运算中的乘法公式有哪些
2.多项式与单项式的除法法则是什么
m(a+b+c)=ma+mb+mc
(m+n)(a+b)=ma+mb+na+nb
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
实践探究
如图,两长方形状的土地长分别为 、
宽都为 ,你能求出它们的总面积吗?
如图,两长方形状的土地长分别为 、
宽都为 ,你能求出它们的总面积吗?
实践探究
思考:从上面的运算结果、运算律能发现了什么?
这两种方法的结果是相同的.可见,单项式乘以多项式(乘法分配律)在二次根式计算中依然适用.
实践探究
实践探究
实际问题:
如图,长方形状的土地长分别为 、
宽都分别为 、 ,你能求出它们的总面积吗?
实践探究
如图,两长方形状的土地长分别为 、
宽都分别为 、 ,你能求出它们的总面积吗?
解:原式
a
b
a
b
b
实践探究
如图,两正方形边长分别为 、 ,你能求出
阴影面积吗?
解原式
实践探究
如图,两正方形边长分别为 、 ,你能求出
阴影面积吗?
实践探究
如图,两正方形边长分别为 、 ,你能求出
所有图形的总面积吗?
解:原式
探究活动4
如图,两正方形边长分别为 、 ,你能求出
所有图形的总面积吗?
思考:
如果整式所有的运算法则中的字母改写成二次根式,是否仍成立呢?为什么?
整式运算中的字母,它的意义十分广泛,可以代表所有一切,当然也可以代表二次根式,所以,整式中的运算法则、运算律也适用于二次根式.
积极思考
思考: 应先计算什么呢?依据是什么?
动手动脑
思考: 应先计算什么呢? 依据是什么?
知识运用
(1) (2)
(3) (4)
知识运用
知识运用
解:
当堂练习
1.下列计算正确的是( )
A.
B.
C.
D.
B
2.已知 , 则 的值为( )
A. 2 B. 4 C. 5 D.7
B
3.计算:
5
4.设 则a b.(填“>”“ < ”或 “= ”)
=
谈谈我们今天的收获和困惑?
回顾反思
通过本节的学习,你认为二次根式运算时应关注哪些方面?通常用到哪些知识?
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a + b)(a - b) = a2 - b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(x + a)(x + b) = x2+(a+b)x+ ab
运算顺序,先算乘方,再算乘除,再算加减,有括号,先算括号里的
课后作业
巩固作业:课本15页习题第4题
拓展作业:1.若,则代数式
2.计算(1)
探究作业:
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式1 = .
变式2 已知 , ,求 的值
变式3 求
探究作业
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式1 = .
解:原式
思维延伸
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式2 已知 , ,求 的值.
思维延伸
我们把两个二次根式的乘积是有理数,积不含二次根式称为它们互为有理化因式。 如 与 互为有理化因式. 的有理化因式是 ;
变式3 求
思维延伸
