1.2 怎样判定三角形相似(3)学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 1.2 怎样判定三角形相似(3)学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 301.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 00:00:00 | ||
图片预览

文档简介
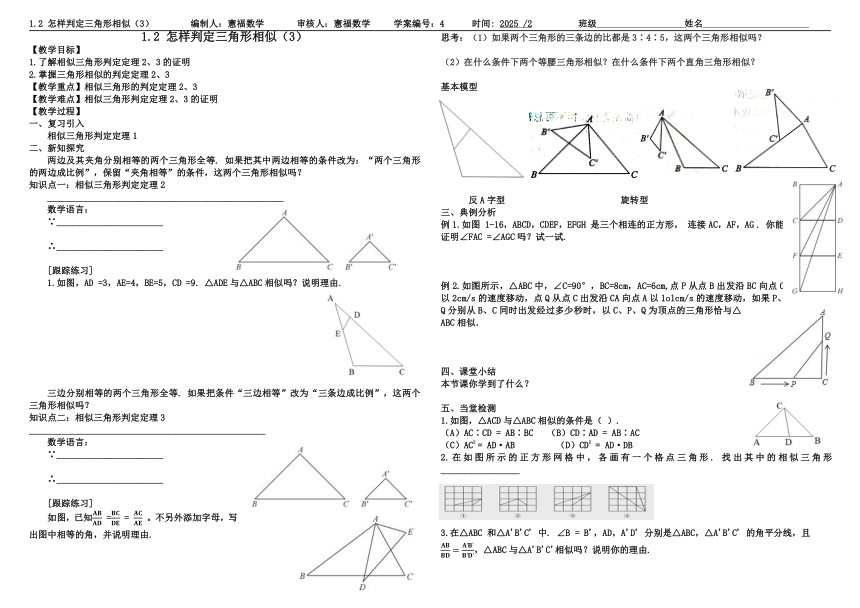
1.2 怎样判定三角形相似(3) 编制人:憲福数学 审核人:憲福数学 学案编号:4 时间: 2025 /2 班级 姓名
1.2 怎样判定三角形相似(3)
【教学目标】
1.了解相似三角形判定定理2、3的证明
2.掌握三角形相似的判定定理2、3
【教学重点】相似三角形的判定定理2、3
【教学难点】相似三角形判定定理2、3的证明
【教学过程】
一、复习引入
相似三角形判定定理1
二、新知探究
两边及其夹角分别相等的两个三角形全等. 如果把其中两边相等的条件改为:“两个三角形的两边成比例”,保留“夹角相等”的条件,这两个三角形相似吗?
知识点一:相似三角形判定定理2
___________________________________________________
数学语言:
∵_______________________
∴_______________________
[跟踪练习]
1.如图,AD =3,AE=4,BE=5,CD =9. △ADE与△ABC相似吗?说明理由.
三边分别相等的两个三角形全等. 如果把条件“三边相等”改为“三条边成比例”,这两个三角形相似吗?
知识点二:相似三角形判定定理3
___________________________________________________
数学语言:
∵_______________________
∴_______________________
[跟踪练习]
如图,已知 = = 。不另外添加字母,写出图中相等的角,并说明理由.
思考:(1)如果两个三角形的三条边的比都是3∶4∶5,这两个三角形相似吗?
(2)在什么条件下两个等腰三角形相似?在什么条件下两个直角三角形相似?
基本模型
反A字型 旋转型
三、典例分析
例1.如图 1-16,ABCD,CDEF,EFGH 是三个相连的正方形, 连接AC,AF,AG . 你能证明∠FAC =∠AGC吗?试一试.
例2.如图所示,△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1olcm/s的速度移动,如果P、Q分别从B、C同时出发经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似.
四、课堂小结
本节课你学到了什么?
五、当堂检测
1.如图,△ACD与△ABC相似的条件是( ).
(A)AC∶CD = AB∶BC (B)CD∶AD = AB∶AC
(C)AC2 = AD·AB (D)CD2 = AD·DB
2.在如图所示的正方形网格中,各画有一个格点三角形. 找出其中的相似三角形_________________
3.在△ABC 和△A'B'C' 中. ∠B = B',AD,A'D' 分别是△ABC,△A'B'C' 的角平分线,且
,△ABC与△A'B'C'相似吗?说明你的理由.
4.已知三角形三边的长分别为 4,5,6,画出与它相似的另一个三角形,使它的一条边长为2 . 你能画出_______符合要求的三角形?
5.如图,在矩形ABCD中,AB=10 cm,AD=20 cm,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1cm,小虫Q每秒走2cm,请问它们同时出发多少秒时,以P,B,Q为顶点的三角形与以A,C,D为顶点的三角形相似
六、课后作业
[基础闯关]
1.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C. D.
2.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )
A.只有(1)相似 B.只有(2)相似 C.都相似 D.都不相似
第1题 第2题
3.一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )
A.30厘米、45厘米 B.40厘米、80厘米 C.80厘米、120厘米 D.90厘米、120厘米
4.△ABC的三边长分别为2、和,△A'B'C′的两边长分别为1和,如果△ABC∽△A'B'C',那么的第三条边的长度等于( )
A. B. C.2 D.
5.如图,小正方形的边长均为1,则下列选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
6.在△ABC和△A′B′C′中,已知∠B=∠B′,AB=6,BC=8,B′C′=4,那么当A′B′=_____时,△ABC∽△A′B′C′.
7.图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是__________.(写出满足条件的所有的点)
8.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,
Q是CD的中点.求证:△ADQ∽△QCP.
9.如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD.求AD的长.
[能力提升]
10.如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
A.∠B=∠D B.=
C.AD∥BC D.∠BAC=∠D
11.如图,点A、B、C、D的坐标分别是(1,7)、(1,1)、(4,1)、(6,1),若△CDE与△ABC相似,则点E的坐标不可能是( )
A.(4,2)B.(6,0)C.(6,4)D.(6,5)
12.在△ABC与△A'B'C'中,有下列条件:①;
②;③A=∠A';④∠C=∠C′.若从中任取两个组成一组,那么能判定△ABC∽△A'B'C'的共有( )组
[培优创新]
14.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=____ 时,以A、D、E为顶点的三角形与△ABC相似.
15.如图,在△ABC中,AB=6cm,BC=12cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q同时从点B开始沿BC边运动,速度为3cm/s的速度,当P、Q运动 时,△ABC与△QBP相似.
1.2 怎样判定三角形相似(3)
【教学目标】
1.了解相似三角形判定定理2、3的证明
2.掌握三角形相似的判定定理2、3
【教学重点】相似三角形的判定定理2、3
【教学难点】相似三角形判定定理2、3的证明
【教学过程】
一、复习引入
相似三角形判定定理1
二、新知探究
两边及其夹角分别相等的两个三角形全等. 如果把其中两边相等的条件改为:“两个三角形的两边成比例”,保留“夹角相等”的条件,这两个三角形相似吗?
知识点一:相似三角形判定定理2
___________________________________________________
数学语言:
∵_______________________
∴_______________________
[跟踪练习]
1.如图,AD =3,AE=4,BE=5,CD =9. △ADE与△ABC相似吗?说明理由.
三边分别相等的两个三角形全等. 如果把条件“三边相等”改为“三条边成比例”,这两个三角形相似吗?
知识点二:相似三角形判定定理3
___________________________________________________
数学语言:
∵_______________________
∴_______________________
[跟踪练习]
如图,已知 = = 。不另外添加字母,写出图中相等的角,并说明理由.
思考:(1)如果两个三角形的三条边的比都是3∶4∶5,这两个三角形相似吗?
(2)在什么条件下两个等腰三角形相似?在什么条件下两个直角三角形相似?
基本模型
反A字型 旋转型
三、典例分析
例1.如图 1-16,ABCD,CDEF,EFGH 是三个相连的正方形, 连接AC,AF,AG . 你能证明∠FAC =∠AGC吗?试一试.
例2.如图所示,△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1olcm/s的速度移动,如果P、Q分别从B、C同时出发经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似.
四、课堂小结
本节课你学到了什么?
五、当堂检测
1.如图,△ACD与△ABC相似的条件是( ).
(A)AC∶CD = AB∶BC (B)CD∶AD = AB∶AC
(C)AC2 = AD·AB (D)CD2 = AD·DB
2.在如图所示的正方形网格中,各画有一个格点三角形. 找出其中的相似三角形_________________
3.在△ABC 和△A'B'C' 中. ∠B = B',AD,A'D' 分别是△ABC,△A'B'C' 的角平分线,且
,△ABC与△A'B'C'相似吗?说明你的理由.
4.已知三角形三边的长分别为 4,5,6,画出与它相似的另一个三角形,使它的一条边长为2 . 你能画出_______符合要求的三角形?
5.如图,在矩形ABCD中,AB=10 cm,AD=20 cm,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1cm,小虫Q每秒走2cm,请问它们同时出发多少秒时,以P,B,Q为顶点的三角形与以A,C,D为顶点的三角形相似
六、课后作业
[基础闯关]
1.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C. D.
2.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )
A.只有(1)相似 B.只有(2)相似 C.都相似 D.都不相似
第1题 第2题
3.一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )
A.30厘米、45厘米 B.40厘米、80厘米 C.80厘米、120厘米 D.90厘米、120厘米
4.△ABC的三边长分别为2、和,△A'B'C′的两边长分别为1和,如果△ABC∽△A'B'C',那么的第三条边的长度等于( )
A. B. C.2 D.
5.如图,小正方形的边长均为1,则下列选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
6.在△ABC和△A′B′C′中,已知∠B=∠B′,AB=6,BC=8,B′C′=4,那么当A′B′=_____时,△ABC∽△A′B′C′.
7.图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是__________.(写出满足条件的所有的点)
8.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,
Q是CD的中点.求证:△ADQ∽△QCP.
9.如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD.求AD的长.
[能力提升]
10.如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
A.∠B=∠D B.=
C.AD∥BC D.∠BAC=∠D
11.如图,点A、B、C、D的坐标分别是(1,7)、(1,1)、(4,1)、(6,1),若△CDE与△ABC相似,则点E的坐标不可能是( )
A.(4,2)B.(6,0)C.(6,4)D.(6,5)
12.在△ABC与△A'B'C'中,有下列条件:①;
②;③A=∠A';④∠C=∠C′.若从中任取两个组成一组,那么能判定△ABC∽△A'B'C'的共有( )组
[培优创新]
14.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=____ 时,以A、D、E为顶点的三角形与△ABC相似.
15.如图,在△ABC中,AB=6cm,BC=12cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q同时从点B开始沿BC边运动,速度为3cm/s的速度,当P、Q运动 时,△ABC与△QBP相似.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
