1.2 怎样判定三角形相似(4)学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 1.2 怎样判定三角形相似(4)学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 270.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 19:37:04 | ||
图片预览

文档简介
1.2 怎样判定三角形相似(4) 编制人:憲福数学 审核人:憲福数学 学案编号:5 时间: 2025 /2 班级 姓名
1.2 怎样判定三角形相似(4)
【教学目标】运用相似三角形的有关知识点解决实际问题。
【教学重点】利用相似三角形测量无法到达的顶部的物体高度的步骤。
【教学难点】利用相似三角形测量无法到达的顶部的物体高度的步骤。
【教学过程】
复习引入
说一说你学过的3个相似三角形判定定理和几何模型
新知探究
知识一:利用相似三角形测量距离
测量 原理 构造相似三角形,利用相似三角形求解
常用 相似 模型
[跟踪练习]
1.如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.6m,BC=14.4m,求建筑物CD的高度。
知识点二:利用相似三角形测量建筑物高度
方法 利用阳光 利用标杆 利用镜子
示意图
注意 同一时刻,同一地点,太阳光线是平行的 观察者的眼睛,标杆的顶端,被测物体的顶端必须三点必须共线
【跟踪练习】
1.小明想利用阳光下的影子来测量光岳楼的高度.如图所示,在某一时刻,他们在阳光下,测得光岳楼OB的影长OC为44米,小明的影长FG为2.4米,其中O、C、F、G在同一直线上,B、O两点在同一直线上,且BO⊥OC,EF⊥FG.已知小明的身高EF为1.8米,求光岳楼的高度.
典型例题
小莹和同学们想利用树影测量树高。在阳光下他们测得一根长1 m的竹竿影长为0.9 m。当他们马上测量树影时,发现树的影子不全落在地面上,有一部分影子落在墙壁上,他们测得地面上的影长为2.7m,墙壁上的影长为1.2 m(如图),树高是多少米?
[跟踪练习]
如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻小明竖起1米高的直杆,量得其影长为0.5米,同时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,则电线杆AB的高为____米.
课堂小结
本节课你有什么收获?
当堂检测
1.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,那么旗杆AB的高为______
2.如图,小亮要测量河流两岸A、B两点的距离,他先从B处出发,沿与AB成90°角的方向向前走30m到C处,立一竹竿,然后按这个方向朝前走10m到D处转90°,沿DE方向再到E处,使A(目标),C(竹竿)与E在同一条直线上,量得DE=17m,则A、B两点间的距离为____
3.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN=______.
第1题 第2题 第3题
4.如图,一天早上,小张正向着教学楼AB走去,他发现教学楼后面有一水塔DC,可过了一会抬头一看:“怎么看不到水塔了”心里很是纳闷.经过了解,教学楼、水塔的高分别为20m和30m,它们之间的距离为30m,小张身高为1.6m(眼睛到头顶的距离忽略不计).小张要想看到水塔,他与教学楼的距离至少应有多少m?
六、课后作业
[基础闯关]
1.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米 B.米 C.36米 D.米
2.如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.6m,BC=14.4m,则建筑物CD的高是____.
3.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为_____.
4.如图,A、B两点被池塘隔开,在AB外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38m,则AB的长为____.
第2题 第3题 第4题
如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为____m.
6.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与直线PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则PQ的长为____m.
第5题 第6题
[能力提升]
7.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.56.5尺 C.6.25尺 D.57.5尺
8.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)请你计算KC的长为______步.
9.如图,是一个常见铁夹的侧面示意图,OA、OB表示铁夹的两个叶片,C是轴,
CD⊥OA于点D,已知DA=40mm,DO=35mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离____.
第7题 第8题 第9题
10.春节期间的一天晚上,小玲和小林去看灯展,当小林站在灯杆AB和灯杆CD之间的F点处,小林的身高为EF,小玲发现了奇怪的一幕:小林在灯A的照射下,影子恰好落在灯杆CD的底部D点处,小林在灯C的照射下,影子恰好落在灯杆AB的底部B点处.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=2m,CD=6m,求小林的身高EF.
[培优创新]
11.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB是多少?
1.2 怎样判定三角形相似(4)
【教学目标】运用相似三角形的有关知识点解决实际问题。
【教学重点】利用相似三角形测量无法到达的顶部的物体高度的步骤。
【教学难点】利用相似三角形测量无法到达的顶部的物体高度的步骤。
【教学过程】
复习引入
说一说你学过的3个相似三角形判定定理和几何模型
新知探究
知识一:利用相似三角形测量距离
测量 原理 构造相似三角形,利用相似三角形求解
常用 相似 模型
[跟踪练习]
1.如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.6m,BC=14.4m,求建筑物CD的高度。
知识点二:利用相似三角形测量建筑物高度
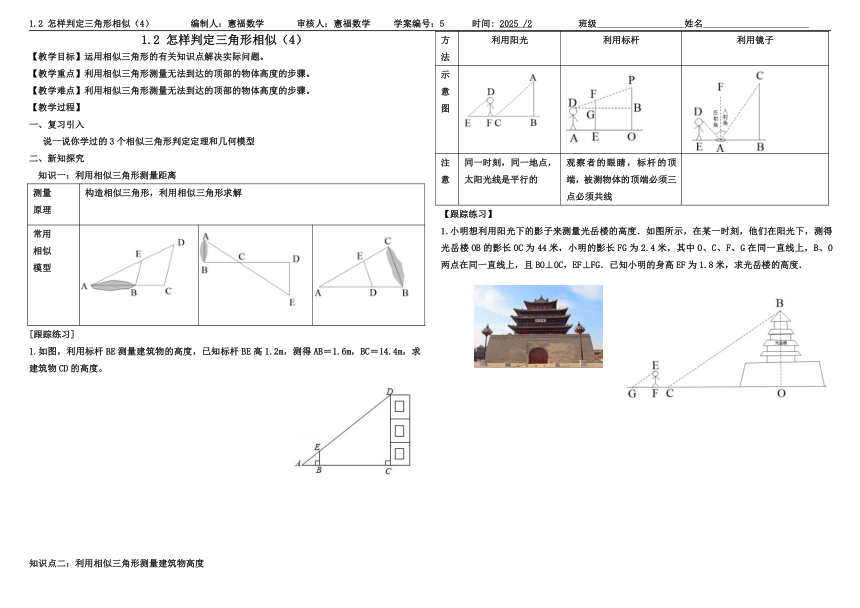
方法 利用阳光 利用标杆 利用镜子
示意图
注意 同一时刻,同一地点,太阳光线是平行的 观察者的眼睛,标杆的顶端,被测物体的顶端必须三点必须共线
【跟踪练习】
1.小明想利用阳光下的影子来测量光岳楼的高度.如图所示,在某一时刻,他们在阳光下,测得光岳楼OB的影长OC为44米,小明的影长FG为2.4米,其中O、C、F、G在同一直线上,B、O两点在同一直线上,且BO⊥OC,EF⊥FG.已知小明的身高EF为1.8米,求光岳楼的高度.
典型例题
小莹和同学们想利用树影测量树高。在阳光下他们测得一根长1 m的竹竿影长为0.9 m。当他们马上测量树影时,发现树的影子不全落在地面上,有一部分影子落在墙壁上,他们测得地面上的影长为2.7m,墙壁上的影长为1.2 m(如图),树高是多少米?
[跟踪练习]
如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻小明竖起1米高的直杆,量得其影长为0.5米,同时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,则电线杆AB的高为____米.
课堂小结
本节课你有什么收获?
当堂检测
1.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,那么旗杆AB的高为______
2.如图,小亮要测量河流两岸A、B两点的距离,他先从B处出发,沿与AB成90°角的方向向前走30m到C处,立一竹竿,然后按这个方向朝前走10m到D处转90°,沿DE方向再到E处,使A(目标),C(竹竿)与E在同一条直线上,量得DE=17m,则A、B两点间的距离为____
3.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN=______.
第1题 第2题 第3题
4.如图,一天早上,小张正向着教学楼AB走去,他发现教学楼后面有一水塔DC,可过了一会抬头一看:“怎么看不到水塔了”心里很是纳闷.经过了解,教学楼、水塔的高分别为20m和30m,它们之间的距离为30m,小张身高为1.6m(眼睛到头顶的距离忽略不计).小张要想看到水塔,他与教学楼的距离至少应有多少m?
六、课后作业
[基础闯关]
1.如图,小明为了测量大楼MN的高度,在离N点30米放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度是( )
A.32米 B.米 C.36米 D.米
2.如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.6m,BC=14.4m,则建筑物CD的高是____.
3.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为_____.
4.如图,A、B两点被池塘隔开,在AB外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38m,则AB的长为____.
第2题 第3题 第4题
如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为____m.
6.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与直线PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则PQ的长为____m.
第5题 第6题
[能力提升]
7.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.56.5尺 C.6.25尺 D.57.5尺
8.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)请你计算KC的长为______步.
9.如图,是一个常见铁夹的侧面示意图,OA、OB表示铁夹的两个叶片,C是轴,
CD⊥OA于点D,已知DA=40mm,DO=35mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离____.
第7题 第8题 第9题
10.春节期间的一天晚上,小玲和小林去看灯展,当小林站在灯杆AB和灯杆CD之间的F点处,小林的身高为EF,小玲发现了奇怪的一幕:小林在灯A的照射下,影子恰好落在灯杆CD的底部D点处,小林在灯C的照射下,影子恰好落在灯杆AB的底部B点处.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=2m,CD=6m,求小林的身高EF.
[培优创新]
11.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB是多少?
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
