第1章 图形的相似 章末复习 学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 第1章 图形的相似 章末复习 学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 389.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 19:39:09 | ||
图片预览

文档简介
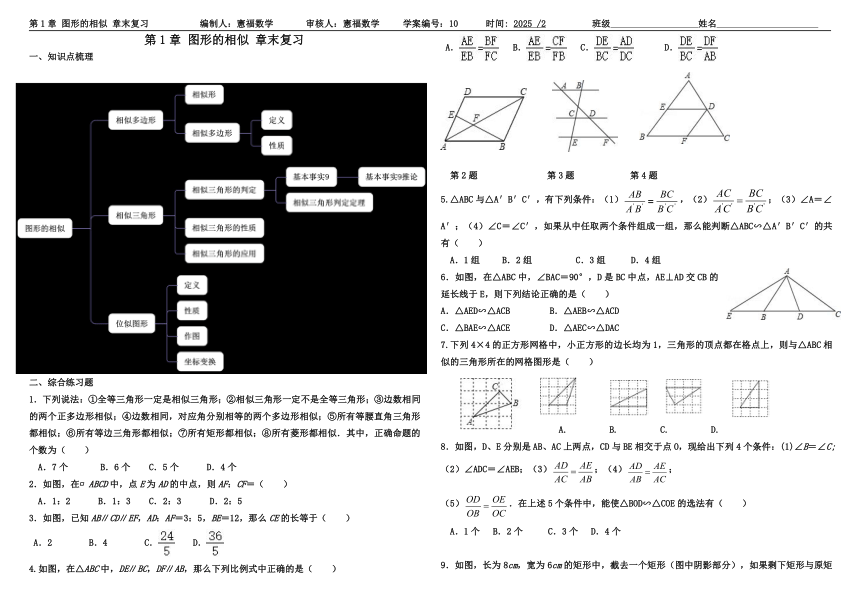
第1章 图形的相似 章末复习 编制人:憲福数学 审核人:憲福数学 学案编号:10 时间: 2025 /2 班级 姓名
第1章 图形的相似 章末复习
一、知识点梳理
二、综合练习题
1.下列说法:①全等三角形一定是相似三角形;②相似三角形一定不是全等三角形;③边数相同的两个正多边形相似;④边数相同,对应角分别相等的两个多边形相似;⑤所有等腰直角三角形都相似;⑥所有等边三角形都相似;⑦所有矩形都相似;⑧所有菱形都相似.其中,正确命题的个数为( )
A.7个 B.6个 C.5个 D.4个
如图,在 ABCD中,点E为AD的中点,则AF:CF=( )
A.1:2 B.1:3 C.2:3 D.2:5
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2 B.4 C. D.
4.如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是( )
A. B. C. D.
第2题 第3题 第4题
5.△ABC与△A′B′C′,有下列条件:(1),(2);(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组 B.2组 C.3组 D.4组
6.如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB的延长线于E,则下列结论正确的是( )
A.△AED∽△ACB B.△AEB∽△ACD
C.△BAE∽△ACE D.△AEC∽△DAC
7.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A. B. C. D.
8.如图,D、E分别是AB、AC上两点,CD与BE相交于点O,现给出下列4个条件:(1)∠B=∠C;(2)∠ADC=∠AEB;(3);(4);
(5).在上述5个条件中,能使△BOD∽△COE的选法有( )
A.1个 B.2个 C.3个 D.4个
9.如图,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
第8题 第9题
10.下列判断中,正确的是( )
A.相似图形一定是位似图形 B.位似图形一定是相似图形
C.全等的图形一定是位似图形 D.位似图形一定是全等图形
11.已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出个( )
A.1个 B.2个 C.4个 D.无数个
12.如图,以某点为位似中心,将△AOB进行位似变换得到△CDE,记△AOB与△CDE对应边的比为k,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(2,2),3
13. 如图,在△ABC中,DE∥BC,BE和CD相交于点F,且S△EFC=3S△EFD,则S△ADE:S△ABC的值为( )S△ADE:S△CDE的值为( )
第12图 第13题
14.若P是Rt△ABC斜边BC上异于B,C的一点,过点P作直线截△ABC,截得的三角形与原△ABC相似,满足这样条件的直线有( )条.
A.1 B.2 C.3 D.4
15.一张等腰三角形纸片,底长15cm,底上高长22.5cm.现沿底边依次从下往上剪宽度均为3cm的矩形纸条,如图剪得纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
16.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且则=( )
A. B. C. D.
17. 如图,边长为9的正三角形ABC,BD=3,∠ADE=60°,则AE为 .
第15图 第16图 第17图
18.△ABC的三边长分别为,,2,△A′B′C′两边长分别是1和,若△ABC与△A′B′C′相似,则△A′B′C′的第三边长应该是 .
19.两个相似多边形的周长之比是2:3,其中一个多边形的最短边长为6,则另一个多边形的最短边长为 ;若两个相似多边形的面积比是2:3,其中一个多边形的最短边长为6,那么另一个多边形的最短边长为 .
20.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,则旗杆AB的高为 m.
21.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为 m.
第20题 第21图
22.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB= 米.
23.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=3AA′,
S△ABC=9,则S△A′B′C′= .
第22题 第23题
24.在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为
25.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△和△;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
以图中的O为位似中心,将△作位似变换且放大到原来的两倍,得到△.
26.如图在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证:
27.星港学校比邻园区海关大楼,星港学校九年级学生小星在学习过“相似”的内容后,也想要利用相似的知识得海关大楼的高度,如图1所示.小星选择把数学和物理知识相结合利用平面镜的镜面反射特点来构造相似,如图2所示.
【问题提出】
问题一:现测量得到,,.问:海关大楼高高为多少?(用,,表示)
【数学思维】
但在进一步观察海关大楼周围的环境之后,小星发现由于条件限制,海关大楼的底部不可到达,所以无法准确测量海关大楼底部到平面镜的距离,如图3所示,在老师帮助下小星进一步完善了自己的想法,得到了方案二:既然无法测量平面镜到海关大楼底部的距离,那就将这部分用其他长度来表示,即构造二次相似,将测量距离进行转化,如图4所示.
问题二:小星测量得到,,,,请你求出海关大楼的高度.
【数学语言】
问题三:小星在求出来数据之后,上网查阅了资料发现海关大楼高度为,请你尝试着分析出现这样误差的原因是什么?
第1章 图形的相似 章末复习
一、知识点梳理
二、综合练习题
1.下列说法:①全等三角形一定是相似三角形;②相似三角形一定不是全等三角形;③边数相同的两个正多边形相似;④边数相同,对应角分别相等的两个多边形相似;⑤所有等腰直角三角形都相似;⑥所有等边三角形都相似;⑦所有矩形都相似;⑧所有菱形都相似.其中,正确命题的个数为( )
A.7个 B.6个 C.5个 D.4个
如图,在 ABCD中,点E为AD的中点,则AF:CF=( )
A.1:2 B.1:3 C.2:3 D.2:5
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2 B.4 C. D.
4.如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是( )
A. B. C. D.
第2题 第3题 第4题
5.△ABC与△A′B′C′,有下列条件:(1),(2);(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组 B.2组 C.3组 D.4组
6.如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB的延长线于E,则下列结论正确的是( )
A.△AED∽△ACB B.△AEB∽△ACD
C.△BAE∽△ACE D.△AEC∽△DAC
7.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A. B. C. D.
8.如图,D、E分别是AB、AC上两点,CD与BE相交于点O,现给出下列4个条件:(1)∠B=∠C;(2)∠ADC=∠AEB;(3);(4);
(5).在上述5个条件中,能使△BOD∽△COE的选法有( )
A.1个 B.2个 C.3个 D.4个
9.如图,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
第8题 第9题
10.下列判断中,正确的是( )
A.相似图形一定是位似图形 B.位似图形一定是相似图形
C.全等的图形一定是位似图形 D.位似图形一定是全等图形
11.已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出个( )
A.1个 B.2个 C.4个 D.无数个
12.如图,以某点为位似中心,将△AOB进行位似变换得到△CDE,记△AOB与△CDE对应边的比为k,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2), C.(2,2),2 D.(2,2),3
13. 如图,在△ABC中,DE∥BC,BE和CD相交于点F,且S△EFC=3S△EFD,则S△ADE:S△ABC的值为( )S△ADE:S△CDE的值为( )
第12图 第13题
14.若P是Rt△ABC斜边BC上异于B,C的一点,过点P作直线截△ABC,截得的三角形与原△ABC相似,满足这样条件的直线有( )条.
A.1 B.2 C.3 D.4
15.一张等腰三角形纸片,底长15cm,底上高长22.5cm.现沿底边依次从下往上剪宽度均为3cm的矩形纸条,如图剪得纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
16.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且则=( )
A. B. C. D.
17. 如图,边长为9的正三角形ABC,BD=3,∠ADE=60°,则AE为 .
第15图 第16图 第17图
18.△ABC的三边长分别为,,2,△A′B′C′两边长分别是1和,若△ABC与△A′B′C′相似,则△A′B′C′的第三边长应该是 .
19.两个相似多边形的周长之比是2:3,其中一个多边形的最短边长为6,则另一个多边形的最短边长为 ;若两个相似多边形的面积比是2:3,其中一个多边形的最短边长为6,那么另一个多边形的最短边长为 .
20.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,则旗杆AB的高为 m.
21.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为 m.
第20题 第21图
22.小慧要测量校园内大树高AB.她运用物理课上学习的“光在反射时,入射角等于反射角”的知识解决了问题.如图,在水平地面上E点处放一面平面镜,镜子与大树的距离EA=8米.小慧沿着AE的方向走到C点时,她刚好能从镜子中看到大树的顶端B.已知CE=2米,小慧的眼睛距地面的高度DC=1.5米.则该棵大树的高度AB= 米.
23.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=3AA′,
S△ABC=9,则S△A′B′C′= .
第22题 第23题
24.在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为
25.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△和△;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
以图中的O为位似中心,将△作位似变换且放大到原来的两倍,得到△.
26.如图在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证:
27.星港学校比邻园区海关大楼,星港学校九年级学生小星在学习过“相似”的内容后,也想要利用相似的知识得海关大楼的高度,如图1所示.小星选择把数学和物理知识相结合利用平面镜的镜面反射特点来构造相似,如图2所示.
【问题提出】
问题一:现测量得到,,.问:海关大楼高高为多少?(用,,表示)
【数学思维】
但在进一步观察海关大楼周围的环境之后,小星发现由于条件限制,海关大楼的底部不可到达,所以无法准确测量海关大楼底部到平面镜的距离,如图3所示,在老师帮助下小星进一步完善了自己的想法,得到了方案二:既然无法测量平面镜到海关大楼底部的距离,那就将这部分用其他长度来表示,即构造二次相似,将测量距离进行转化,如图4所示.
问题二:小星测量得到,,,,请你求出海关大楼的高度.
【数学语言】
问题三:小星在求出来数据之后,上网查阅了资料发现海关大楼高度为,请你尝试着分析出现这样误差的原因是什么?
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
