1.1 相似多边形 学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 1.1 相似多边形 学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 20:00:17 | ||
图片预览

文档简介
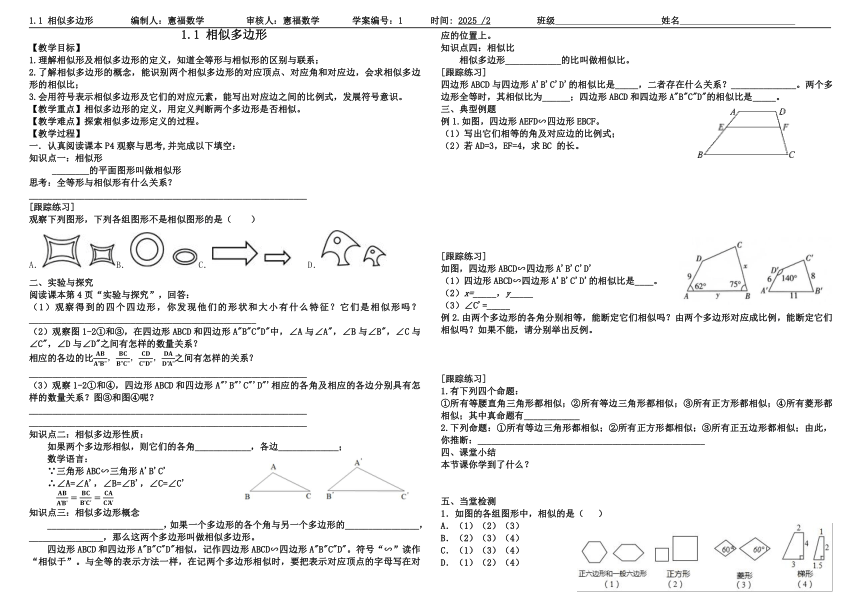
1.1 相似多边形 编制人:憲福数学 审核人:憲福数学 学案编号:1 时间: 2025 /2 班级 姓名
1.1 相似多边形
【教学目标】
1.理解相似形及相似多边形的定义,知道全等形与相似形的区别与联系;
2.了解相似多边形的概念,能识别两个相似多边形的对应顶点、对应角和对应边,会求相似多边形的相似比;
3.会用符号表示相似多边形及它们的对应元素,能写出对应边之间的比例式,发展符号意识。
【教学重点】相似多边形的定义,用定义判断两个多边形是否相似。
【教学难点】探索相似多边形定义的过程。
【教学过程】
一.认真阅读课本P4观察与思考,并完成以下填空:
知识点一:相似形
________的平面图形叫做相似形
思考:全等形与相似形有什么关系?
____________________________________________________________
[跟踪练习]
观察下列图形,下列各组图形不是相似图形的是( )
A.B.C. D.
实验与探究
阅读课本第4页“实验与探究”,回答:
(1)观察得到的四个四边形,你发现他们的形状和大小有什么特征?它们是相似形吗?_________________________________________________
(2)观察图1-2①和③,在四边形ABCD和四边形A"B"C"D"中,∠A与∠A",∠B与∠B",∠C与∠C",∠D与∠D"之间有怎样的数量关系?
相应的各边的比,,,之间有怎样的关系?
____________________________________________________________
观察1-2①和④,四边形ABCD和四边形A"'B"'C"'D"'相应的各角及相应的各边分别具有怎样的数量关系?图③和图④呢?
____________________________________________________________
____________________________________________________________
知识点二:相似多边形性质:
如果两个多边形相似,则它们的各角____________,各边_____________;
数学语言:
∵三角形ABC∽三角形A'B'C'
∴∠A=∠A',∠B=∠B',∠C=∠C'
知识点三:相似多边形概念
_________________________,如果一个多边形的各个角与另一个多边形的________________,________________,那么这两个多边形叫做相似多边形。
四边形ABCD和四边形A"B"C"D"相似,记作四边形ABCD∽四边形A"B"C"D"。符号“∽”读作“相似于”。与全等的表示方法一样,在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上。
知识点四:相似比
相似多边形____________的比叫做相似比。
[跟踪练习]
四边形ABCD与四边形A'B'C'D'的相似比是_____,二者存在什么关系?______________。两个多边形全等时,其相似比为______;四边形ABCD和四边形A"B"C"D"的相似比是_____。
典型例题
例1.如图,四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC 的长。
[跟踪练习]
如图,四边形ABCD∽四边形A'B'C'D'
(1)四边形ABCD∽四边形A'B'C'D'的相似比是____。
(2)x=_____,y_____
(3)∠C'=_____
例2.由两个多边形的各角分别相等,能断定它们相似吗?由两个多边形对应成比例,能断定它们相似吗?如果不能,请分别举出反例。
[跟踪练习]
1.有下列四个命题:
①所有等腰直角三角形都相似;②所有等边三角形都相似;③所有正方形都相似;④所有菱形都相似;其中真命题有____________
2.下列命题:①所有等边三角形都相似;②所有正方形都相似;③所有正五边形都相似;由此,你推断:_________________________________________________
四、课堂小结
本节课你学到了什么?
五、当堂检测
1.如图的各组图形中,相似的是( )
A.(1)(2)(3)
B.(2)(3)(4)
C.(1)(3)(4)
D.(1)(2)(4)
2.如图,四边形ABCD∽四边形A1B1C1D1, AB=12,CD=15,A1B1=9,则边C1D1的长是_______
3.如图,AC是四边形ABCD的对角线,A'、B'分别是AC、BC的中点,D'在CD上,且四边形ABCD与四边形A'B'C'D'相似。四边形ABCD与四边形A'B'C'D'相似比是__________。
第2题 第3题
5.如图,矩形的草坪长20m,宽10m,沿草坪四周外围有1m的环行小路,小路的内外边缘所成的矩形相似吗?为什么?
6.如图,把矩形ABCD对折,折痕为MN,矩形DMNC∽矩形ABCD,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比。
六、课后作业
[基础闯关]
1.如图所示的三个矩形中,是相似的是( )
A.甲与乙
B.乙与丙
C.甲与丙
D.甲乙丙都相似
2.如图的两个四边形相似,则∠α的度数是( )
A.87°
B.60°
C.75°
D.120°
3.若一个三角形三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为( )A.15 B.10 C.9 D.3
4.要做甲乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为:50cm、60cm、80cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架一共有( )
A.1种 B.2种 C.3种 D.4种
5.两个相似多边形的一组对应边分别为3cm和2cm,那么它们的相似比是( )
A. B. C. D.
6.若两个相似多边形的最长边的长度分别为10和20,且其中一个多边形的最短边长为4,则另一个多边形的最短边长为_____。
7.三角形与四边形相似吗?等边三角形与直角三角形能相似吗?为什么?
8.如图,△ABC∽△DFE,点A与点D,点B与点F是对应点。请写出它们的对应角,对应边及对应边之间的比例式。
9.如果五边形ABCDE∽五边形A'B'C'D'E',且五边形 ABCDE 与 A'B'C'D'E' 的相似比为 k1,五边形A'B'C'D'E'与ABCDE的相似比为k2,那么k1与k2满足怎样的数量关系?
10.如图,已知△DEA ∽△BCA,
(1)BC∥DE吗?为什么?
(2)如果BC = 3.6,ED = 2.4,AE = 5,求AC的长.
如图,四边形ABCD∽四边形PGRS,BC=8,GR=10,PS=6,∠B=64°.
求:(1)∠Q的度数; (2)AD的长;
(3)求四边形ABCD与四边形PGRS的相似比.
[能力提升]
12.如图,△BEA∽△BAD,写出图中所有相等的角和成比例线段的比例式.
[培优创新]
13.已知△ABC ∽△DEF,如果BC = 3,CA = 4,AB = 6,△DEF的最短边长为2 .
求: (1)△DEF各边的长; (2)△ABC与△DEF的相似比.
1.1 相似多边形
【教学目标】
1.理解相似形及相似多边形的定义,知道全等形与相似形的区别与联系;
2.了解相似多边形的概念,能识别两个相似多边形的对应顶点、对应角和对应边,会求相似多边形的相似比;
3.会用符号表示相似多边形及它们的对应元素,能写出对应边之间的比例式,发展符号意识。
【教学重点】相似多边形的定义,用定义判断两个多边形是否相似。
【教学难点】探索相似多边形定义的过程。
【教学过程】
一.认真阅读课本P4观察与思考,并完成以下填空:
知识点一:相似形
________的平面图形叫做相似形
思考:全等形与相似形有什么关系?
____________________________________________________________
[跟踪练习]
观察下列图形,下列各组图形不是相似图形的是( )
A.B.C. D.
实验与探究
阅读课本第4页“实验与探究”,回答:
(1)观察得到的四个四边形,你发现他们的形状和大小有什么特征?它们是相似形吗?_________________________________________________
(2)观察图1-2①和③,在四边形ABCD和四边形A"B"C"D"中,∠A与∠A",∠B与∠B",∠C与∠C",∠D与∠D"之间有怎样的数量关系?
相应的各边的比,,,之间有怎样的关系?
____________________________________________________________
观察1-2①和④,四边形ABCD和四边形A"'B"'C"'D"'相应的各角及相应的各边分别具有怎样的数量关系?图③和图④呢?
____________________________________________________________
____________________________________________________________
知识点二:相似多边形性质:
如果两个多边形相似,则它们的各角____________,各边_____________;
数学语言:
∵三角形ABC∽三角形A'B'C'
∴∠A=∠A',∠B=∠B',∠C=∠C'
知识点三:相似多边形概念
_________________________,如果一个多边形的各个角与另一个多边形的________________,________________,那么这两个多边形叫做相似多边形。
四边形ABCD和四边形A"B"C"D"相似,记作四边形ABCD∽四边形A"B"C"D"。符号“∽”读作“相似于”。与全等的表示方法一样,在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上。
知识点四:相似比
相似多边形____________的比叫做相似比。
[跟踪练习]
四边形ABCD与四边形A'B'C'D'的相似比是_____,二者存在什么关系?______________。两个多边形全等时,其相似比为______;四边形ABCD和四边形A"B"C"D"的相似比是_____。
典型例题
例1.如图,四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC 的长。
[跟踪练习]
如图,四边形ABCD∽四边形A'B'C'D'
(1)四边形ABCD∽四边形A'B'C'D'的相似比是____。
(2)x=_____,y_____
(3)∠C'=_____
例2.由两个多边形的各角分别相等,能断定它们相似吗?由两个多边形对应成比例,能断定它们相似吗?如果不能,请分别举出反例。
[跟踪练习]
1.有下列四个命题:
①所有等腰直角三角形都相似;②所有等边三角形都相似;③所有正方形都相似;④所有菱形都相似;其中真命题有____________
2.下列命题:①所有等边三角形都相似;②所有正方形都相似;③所有正五边形都相似;由此,你推断:_________________________________________________
四、课堂小结
本节课你学到了什么?
五、当堂检测
1.如图的各组图形中,相似的是( )
A.(1)(2)(3)
B.(2)(3)(4)
C.(1)(3)(4)
D.(1)(2)(4)
2.如图,四边形ABCD∽四边形A1B1C1D1, AB=12,CD=15,A1B1=9,则边C1D1的长是_______
3.如图,AC是四边形ABCD的对角线,A'、B'分别是AC、BC的中点,D'在CD上,且四边形ABCD与四边形A'B'C'D'相似。四边形ABCD与四边形A'B'C'D'相似比是__________。
第2题 第3题
5.如图,矩形的草坪长20m,宽10m,沿草坪四周外围有1m的环行小路,小路的内外边缘所成的矩形相似吗?为什么?
6.如图,把矩形ABCD对折,折痕为MN,矩形DMNC∽矩形ABCD,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比。
六、课后作业
[基础闯关]
1.如图所示的三个矩形中,是相似的是( )
A.甲与乙
B.乙与丙
C.甲与丙
D.甲乙丙都相似
2.如图的两个四边形相似,则∠α的度数是( )
A.87°
B.60°
C.75°
D.120°
3.若一个三角形三边之比为3:5:7,与它相似的三角形的最长边的长为21,则最短边的长为( )A.15 B.10 C.9 D.3
4.要做甲乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为:50cm、60cm、80cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架一共有( )
A.1种 B.2种 C.3种 D.4种
5.两个相似多边形的一组对应边分别为3cm和2cm,那么它们的相似比是( )
A. B. C. D.
6.若两个相似多边形的最长边的长度分别为10和20,且其中一个多边形的最短边长为4,则另一个多边形的最短边长为_____。
7.三角形与四边形相似吗?等边三角形与直角三角形能相似吗?为什么?
8.如图,△ABC∽△DFE,点A与点D,点B与点F是对应点。请写出它们的对应角,对应边及对应边之间的比例式。
9.如果五边形ABCDE∽五边形A'B'C'D'E',且五边形 ABCDE 与 A'B'C'D'E' 的相似比为 k1,五边形A'B'C'D'E'与ABCDE的相似比为k2,那么k1与k2满足怎样的数量关系?
10.如图,已知△DEA ∽△BCA,
(1)BC∥DE吗?为什么?
(2)如果BC = 3.6,ED = 2.4,AE = 5,求AC的长.
如图,四边形ABCD∽四边形PGRS,BC=8,GR=10,PS=6,∠B=64°.
求:(1)∠Q的度数; (2)AD的长;
(3)求四边形ABCD与四边形PGRS的相似比.
[能力提升]
12.如图,△BEA∽△BAD,写出图中所有相等的角和成比例线段的比例式.
[培优创新]
13.已知△ABC ∽△DEF,如果BC = 3,CA = 4,AB = 6,△DEF的最短边长为2 .
求: (1)△DEF各边的长; (2)△ABC与△DEF的相似比.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
