1.4 图形的位似(2)学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 1.4 图形的位似(2)学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 319.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-14 20:02:41 | ||
图片预览

文档简介
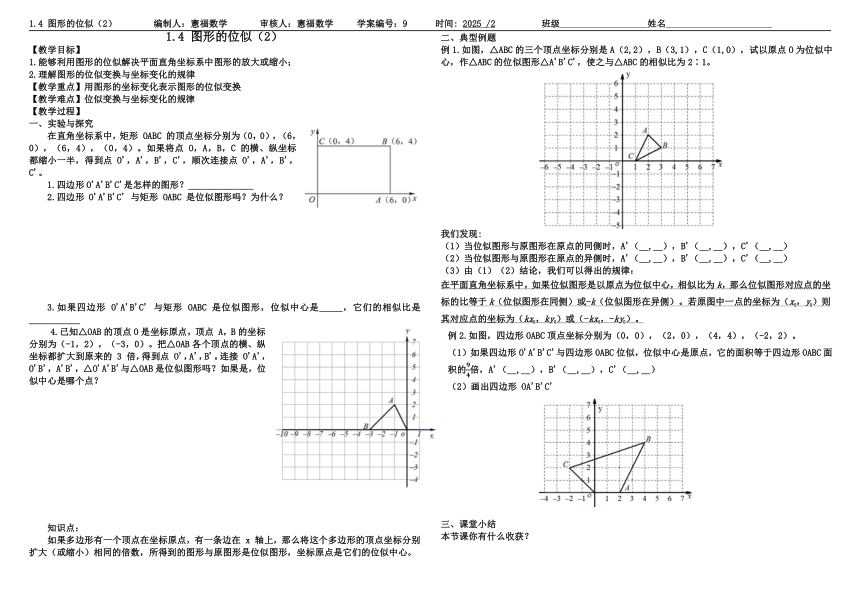
1.4 图形的位似(2) 编制人:憲福数学 审核人:憲福数学 学案编号:9 时间: 2025 /2 班级 姓名
1.4 图形的位似(2)
【教学目标】
1.能够利用图形的位似解决平面直角坐标系中图形的放大或缩小;
2.理解图形的位似变换与坐标变化的规律
【教学重点】用图形的坐标变化表示图形的位似变换
【教学难点】位似变换与坐标变化的规律
【教学过程】
一、实验与探究
在直角坐标系中,矩形 OABC 的顶点坐标分别为(0,0),(6,0),(6,4),(0,4)。如果将点 O,A,B,C 的横、纵坐标都缩小一半,得到点 O',A',B',C',顺次连接点 O',A',B',C'。
1.四边形O'A'B'C'是怎样的图形?______________
2.四边形 O'A'B'C' 与矩形 OABC 是位似图形吗?为什么?
3.如果四边形 O'A'B'C' 与矩形 OABC 是位似图形,位似中心是_____,它们的相似比是___________
4.已知△OAB的顶点O是坐标原点,顶点 A,B的坐标分别为(-1,2),(-3,0)。把△OAB各个顶点的横、纵坐标都扩大到原来的 3 倍,得到点 O',A',B'。连接 O'A',O'B',A'B',△O'A'B'与△OAB是位似图形吗?如果是,位似中心是哪个点?
知识点:
如果多边形有一个顶点在坐标原点,有一条边在 x 轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心。
二、典型例题
例1.如图,△ABC的三个顶点坐标分别是A(2,2),B(3,1),C(1,0),试以原点O为位似中心,作△ABC的位似图形△A'B'C',使之与△ABC的相似比为2∶1。
我们发现:
(1)当位似图形与原图形在原点的同侧时,A'(__,__),B'(__,__),C'(__,__)
(2)当位似图形与原图形在原点的异侧时,A'(__,__),B'(__,__),C'(__,__)
(3)由(1)(2)结论,我们可以得出的规律:
在平面直角坐标系中,如果位似图形是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k(位似图形在同侧)或-k(位似图形在异侧)。若原图中一点的坐标为(x0,y0)则其对应点的坐标为(kx0,ky0)或(-kx0,-ky0)。
例2.如图,四边形OABC顶点坐标分别为(0,0),(2,0),(4,4),(-2,2)。
(1)如果四边形O'A'B'C'与四边形OABC位似,位似中心是原点,它的面积等于四边形OABC面积的倍,A'(__,__),B'(__,__),C'(__,__)
(2)画出四边形 OA'B'C'
课堂小结
本节课你有什么收获?
四、当堂检测
1.在直角坐标系中,已知点 E(-4,2),F(-1,-1)。以O为位似中心,把△EFO 缩小到原来的,求点E,F的对应点E'坐标为_______________________,F'坐标为_____________________
2.如图, OABC的一个顶点是坐标原点,点A的坐标是(4,0),点C的坐标是(2,-2)。(1)B(__,__);
(2)画出以点 O 为位似中心,与 OABC位似的图形,使它与 OABC的相似比为1∶2 。
五、课后作业
[基础闯关]★
1.判断满足下列条件的两个三角形是不是位似图形,如果是,指出位似中心。
(1)如图①所示,AB,CD相交于点O,且∠B =∠D,AD = CB;
(2)如图②所示,AB,CD相交于点O,且∠B =∠A。
2.如图,在△ABC中,E,F 是 AB 的三等分点,FH∥EG∥AC 。
(1)四边形EFHG与四边形FACH是位似图形吗?为什么?
(2)指出图中所有的位似图形。
3.在如图所示的方格纸上,以点O为位似中心,画出与五边形ABCDE位似的图形,使它的周长等于五边形 ABCDE 周长的。
4. 如图,△ABC为正三角形,点A与B的坐标分别为(-1,0),(1,0)。以点C 为位似中心,在点C下方画出一个与△ABC 位似的图形,使它与△ABC的相似比为2∶1。
5.如图,点O是等边三角形ABC 的中心,P,Q,R分别是OA,OB,OC的中点。说明△ABC与△PQR是位似图形,并求出它们的相似比。
6.如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是______________
7.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,点A,B,A′,B′均在图中的格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为______________
8.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为______________
9.如图,在平面直角坐标系中,△OAB与△OCD位似,位似中心是坐标原点O.若点A(4,0),点C(2,0),则△OAB与△OCD周长的比值是______________.
10.如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是______________.
11.如图,在平面直角坐标系中,正方形ABCD的对角线相交于点E,A(2,0),B(6,0),将正方形ABCD以A为位似中心,1:2为位似比缩小,点E的对应点E′的坐标是______________.
第9题 第10题 第11题
12.在平面直角坐标系中,已知矩形OA1B1C1与矩形OABC关于坐标原点O位似,且矩形OA1B1C1的面积等于矩形OABC面积的4倍,若矩形OABC的顶点B的坐标为B(8,6),则B的对应点B1的坐标为______________.
13.如图,△ABC的三个顶点的坐标分别为A(﹣2,4),B(﹣3,1),C(﹣1,1),以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A'B'C'.画出放大后的图形,并写出A',B',C'的坐标.
[能力提升]★★★
14.如图,在6×8 的网格图中,每个小正方形的边长均为1。点O和△ABC的顶点均是格点。以O为位似中心,在网格中画出与△ABC位似,且相似比为 1∶2 的顶点均是格点的三角形。
15.如图,在平面直角坐标系中,O为坐标原点,矩形ABCD与矩形EFGO是位似图形,位似中心在y轴上,对应点B、F的坐标分别为(﹣4,4)、(2,1),则位似中心的坐标为_____________
16.如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且,若点A(﹣1,0),点C(,1),则A′C′=_____________.
第15题 第16题 第17题
17.如图,四边形ABCD是正方形,原点O是四边形ABCD和A′B′C′D′的位似中心,点B、C的坐标分别为(﹣8,2),(﹣4,0),点B′是点B的对应点,且点B′的横坐标为﹣1,则四边形A′B′C′D′的周长为_____________.
18.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B'的横坐标是 _____________.
[培优创新]★★★★
20.如图,在平面直角坐标系xOy中,以O为位似中心,将边长为8的等边三角形OAB作n次位似变换,经第一次变换后得到等边三角形OA1B1,其边长OA1缩小为OA的,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(,0),则n的值是_____________
1.4 图形的位似(2)
【教学目标】
1.能够利用图形的位似解决平面直角坐标系中图形的放大或缩小;
2.理解图形的位似变换与坐标变化的规律
【教学重点】用图形的坐标变化表示图形的位似变换
【教学难点】位似变换与坐标变化的规律
【教学过程】
一、实验与探究
在直角坐标系中,矩形 OABC 的顶点坐标分别为(0,0),(6,0),(6,4),(0,4)。如果将点 O,A,B,C 的横、纵坐标都缩小一半,得到点 O',A',B',C',顺次连接点 O',A',B',C'。
1.四边形O'A'B'C'是怎样的图形?______________
2.四边形 O'A'B'C' 与矩形 OABC 是位似图形吗?为什么?
3.如果四边形 O'A'B'C' 与矩形 OABC 是位似图形,位似中心是_____,它们的相似比是___________
4.已知△OAB的顶点O是坐标原点,顶点 A,B的坐标分别为(-1,2),(-3,0)。把△OAB各个顶点的横、纵坐标都扩大到原来的 3 倍,得到点 O',A',B'。连接 O'A',O'B',A'B',△O'A'B'与△OAB是位似图形吗?如果是,位似中心是哪个点?
知识点:
如果多边形有一个顶点在坐标原点,有一条边在 x 轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心。
二、典型例题
例1.如图,△ABC的三个顶点坐标分别是A(2,2),B(3,1),C(1,0),试以原点O为位似中心,作△ABC的位似图形△A'B'C',使之与△ABC的相似比为2∶1。
我们发现:
(1)当位似图形与原图形在原点的同侧时,A'(__,__),B'(__,__),C'(__,__)
(2)当位似图形与原图形在原点的异侧时,A'(__,__),B'(__,__),C'(__,__)
(3)由(1)(2)结论,我们可以得出的规律:
在平面直角坐标系中,如果位似图形是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k(位似图形在同侧)或-k(位似图形在异侧)。若原图中一点的坐标为(x0,y0)则其对应点的坐标为(kx0,ky0)或(-kx0,-ky0)。
例2.如图,四边形OABC顶点坐标分别为(0,0),(2,0),(4,4),(-2,2)。
(1)如果四边形O'A'B'C'与四边形OABC位似,位似中心是原点,它的面积等于四边形OABC面积的倍,A'(__,__),B'(__,__),C'(__,__)
(2)画出四边形 OA'B'C'
课堂小结
本节课你有什么收获?
四、当堂检测
1.在直角坐标系中,已知点 E(-4,2),F(-1,-1)。以O为位似中心,把△EFO 缩小到原来的,求点E,F的对应点E'坐标为_______________________,F'坐标为_____________________
2.如图, OABC的一个顶点是坐标原点,点A的坐标是(4,0),点C的坐标是(2,-2)。(1)B(__,__);
(2)画出以点 O 为位似中心,与 OABC位似的图形,使它与 OABC的相似比为1∶2 。
五、课后作业
[基础闯关]★
1.判断满足下列条件的两个三角形是不是位似图形,如果是,指出位似中心。
(1)如图①所示,AB,CD相交于点O,且∠B =∠D,AD = CB;
(2)如图②所示,AB,CD相交于点O,且∠B =∠A。
2.如图,在△ABC中,E,F 是 AB 的三等分点,FH∥EG∥AC 。
(1)四边形EFHG与四边形FACH是位似图形吗?为什么?
(2)指出图中所有的位似图形。
3.在如图所示的方格纸上,以点O为位似中心,画出与五边形ABCDE位似的图形,使它的周长等于五边形 ABCDE 周长的。
4. 如图,△ABC为正三角形,点A与B的坐标分别为(-1,0),(1,0)。以点C 为位似中心,在点C下方画出一个与△ABC 位似的图形,使它与△ABC的相似比为2∶1。
5.如图,点O是等边三角形ABC 的中心,P,Q,R分别是OA,OB,OC的中点。说明△ABC与△PQR是位似图形,并求出它们的相似比。
6.如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是______________
7.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,点A,B,A′,B′均在图中的格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为______________
8.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为______________
9.如图,在平面直角坐标系中,△OAB与△OCD位似,位似中心是坐标原点O.若点A(4,0),点C(2,0),则△OAB与△OCD周长的比值是______________.
10.如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是______________.
11.如图,在平面直角坐标系中,正方形ABCD的对角线相交于点E,A(2,0),B(6,0),将正方形ABCD以A为位似中心,1:2为位似比缩小,点E的对应点E′的坐标是______________.
第9题 第10题 第11题
12.在平面直角坐标系中,已知矩形OA1B1C1与矩形OABC关于坐标原点O位似,且矩形OA1B1C1的面积等于矩形OABC面积的4倍,若矩形OABC的顶点B的坐标为B(8,6),则B的对应点B1的坐标为______________.
13.如图,△ABC的三个顶点的坐标分别为A(﹣2,4),B(﹣3,1),C(﹣1,1),以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A'B'C'.画出放大后的图形,并写出A',B',C'的坐标.
[能力提升]★★★
14.如图,在6×8 的网格图中,每个小正方形的边长均为1。点O和△ABC的顶点均是格点。以O为位似中心,在网格中画出与△ABC位似,且相似比为 1∶2 的顶点均是格点的三角形。
15.如图,在平面直角坐标系中,O为坐标原点,矩形ABCD与矩形EFGO是位似图形,位似中心在y轴上,对应点B、F的坐标分别为(﹣4,4)、(2,1),则位似中心的坐标为_____________
16.如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且,若点A(﹣1,0),点C(,1),则A′C′=_____________.
第15题 第16题 第17题
17.如图,四边形ABCD是正方形,原点O是四边形ABCD和A′B′C′D′的位似中心,点B、C的坐标分别为(﹣8,2),(﹣4,0),点B′是点B的对应点,且点B′的横坐标为﹣1,则四边形A′B′C′D′的周长为_____________.
18.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B'的横坐标是 _____________.
[培优创新]★★★★
20.如图,在平面直角坐标系xOy中,以O为位似中心,将边长为8的等边三角形OAB作n次位似变换,经第一次变换后得到等边三角形OA1B1,其边长OA1缩小为OA的,经第二次变换后得到等边三角形OA2B2,其边长OA2缩小为OA1的,经第三次变换后得到等边三角形OA3B3,其边长OA3缩小为OA2的,…按此规律,经第n次变换后,所得等边出角形OAnBn.的顶点An的坐标为(,0),则n的值是_____________
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
